4 Flow in the oceans
One of the most fascinating aspects of the oceans are that they always appear to be moving. At the large scale, we experience this movement in the major ocean currents such as the Gulf Stream. Much of the energy in the moving ocean, however, is present on a smaller scale: circulating eddies a few tens of kilometres in size. The energy that drives this movement is ultimately derived from the heat of the sun and the rotation of the earth.
4.1 Making ocean water flow
The great surface ocean currents, for example the Gulf Stream in the north Atlantic and the Kuroshio in the north Pacific, are primarily driven by the wind. Ocean surface winds in the Atlantic and Pacific (both north and south) are, in a general sense, towards the west near the Equator (the trade winds) and towards the east at higher latitudes (the westerlies; see Figure 4.1). This produces a clockwise circulation in the north Atlantic and the north Pacific, and anti-clockwise circulation in the southern parts of both oceans. These great circular flows in the major ocean basins are called wind-driven gyres, a term coined by the American physical oceanographer, Walter Munk. The Indian Ocean is somewhat different and has seasonally varying currents that respond to changes in wind direction associated with the monsoon. It was in fact the response of the Indian Ocean to the wind that helped to convince oceanographers that surface currents were primarily wind-driven. The wind-driven circulation in the Atlantic and Pacific, however, is not symmetrical. The currents on the western side of these oceans are much faster and more intense than those on the east. In the north Atlantic, for example, the Gulf Stream in the west is much more obvious than the gentle southward flow that occurs down the coast of Europe and North Africa. The reason why this should be so evaded oceanographers for many years until Henry Stommel, an American oceanographer, proposed a solution in 1948. The western intensification of ocean currents is caused by the change in angular momentum of the water as it flows poleward (see text box).

Figure 4.1 The prevailing wind patterns over the north Atlantic drive a predominantly clockwise flow in the surface layer.
Figure 4.2 shows a schematic of the major currents of the north Atlantic. Surface currents are marked in red and these show the progress of the Gulf Stream across the north Atlantic. The flow divides at the latitude of Spain, and it is the rather weaker North Atlantic Drift that brings relatively warm water from the south and west to the British Isles. The rest of the Gulf Stream water completes a circuit of the ocean in a great clockwise gyre.

Figure 4.2 Schematic of the circulation in the north Atlantic showing surface currents in red and deep flows in blue.
Why there is a Gulf Stream
In the Pacific and Atlantic Oceans (both north and south) the current on the western side of the ocean is much faster and more intense than anywhere else. We shall explain as simply as possible why this is, using the Gulf Stream as an example.
A vertical column on the surface of the earth possesses angular momentum imparted by the Earth’s spin (oceanographers prefer the word vorticity, but we shall stick with the hopefully more familiar term angular momentum). The angular momentum is greatest at the poles, where the column makes a complete turn once per day, and is zero at the Equator. As the Gulf Stream flows northwards up the east coast of America, therefore, it has to acquire anti-clockwise angular momentum to keep up with the increasing effect of the Earth’s spin. The winds don’t help, because the prevailing winds impart clockwise momentum, and it is this that drives the gyre. Instead, the Gulf Stream acquires anti-clockwise angular momentum through friction. By pressing against the east coast of America, anti-clockwise spinning eddies are generated which provide the necessary angular momentum. In order to provide enough angular momentum to allow for the change of latitude and counteract the clockwise momentum put in by the wind, a fast narrow flow is required to generate a lot of friction.
On the eastern side of the ocean, the equator-ward flow needs to lose anti-clockwise momentum. The effect of the clockwise wind will help to do this, and so here the friction is not needed (in fact it will produce anti-clockwise momentum, which is the opposite of what is needed). As a result, the current down the east side of the ocean is broad and slow to minimise frictional effects. To summarise, to preserve angular momentum, poleward flowing currents need a lot of friction with the continental boundary and Equatorward-flowing currents do not.
The second great mover of ocean water is a difference in density. Dense water formed by cooling at high latitudes sinks and contributes to the thermohaline circulation, part of which is shown in blue in Figure 4.2 contributing to North Atlantic Deep Water flowing southwards along the western side of the Atlantic. As we discussed in Chapter 1, a source of energy is needed to drive this circulation, and this is thought to be the tidal energy generated within the body of the ocean. Tidal forces are, in fact, the third of the great forces that can drive flow in the ocean, and we deal with these in Chapter 5.
4.2 Observing ocean currents
Oceanographers observe ocean currents directly in two ways. The first is to use a current meter at a fixed point. In its simplest form a current meter has a propeller that turns in the current; the number of turns of the propeller in a given time is counted and this is proportional to the current speed. The current meter would normally be fixed on a mooring attached to the seabed. Current measurements made at a fixed point in this way are called Eulerian observations. Typical current speeds range from about 200 cm s–1 in strong currents like the Gulf Stream to less than 1 cm s–1 in the deep parts of the ocean. In shallow water, Eulerian measurements of current velocity can also be made with Acoustic Doppler techniques (see Chapter 15).
The second way to measure ocean currents is with a drifting buoy that can be tracked by satellite. Drifting buoys follow the current: they don’t stay in one place. Measurements of ocean currents made in this way are called Lagrangian. A very successful international collaboration on ocean drifters is the Argo collection of a large number (several thousand) of small drifting probes. The probes drift at depths of up to 2 km, returning to the surface to transmit data on water temperature and salinity. This data is made freely available via the internet (Figure 4.3).
The strength of ocean currents can usefully be expressed as the volume of water transported in a given time. The volume transport in a current is equal to the flow speed multiplied by the cross-sectional area of the current. Millions of cubic metres per second (m3/s) are transported by major ocean currents, and we have a special unit for recording this, the Sverdrup (symbol is Sv), named after the Norwegian oceanographer, Harald Sverdrup. One Sv is one million m3 s–1. The volume transports of some selected ocean currents are shown in Table 4.1.
The effect of surface ocean currents can be seen in the distribution of surface properties such as temperature. Currents moving from low to high latitudes carry warm water. The warm waters of the Gulf Stream can be made out in infra-red satellite images (Figure 4.4).

Figure 4.3 Cross section of an Argo float, a free-floating oceanographic probe.
Table 4.1: Volume transports of some selected ocean currents.
| Volume transport (Sv) | |
| The Gulf Stream (off Cape Hatteras) | 85 |
| wThe Kuroshio (Japan) | 40 |
| Antarctic Circumpolar Current | 110 |

Figure 4.4 Infra-red satellite image of the north-west Atlantic showing sea surface temperature. The path of the Gulf Stream as it leaves the coast of the United States and travels eastwards and northwards towards Europe can be seen.
4.3 The continuity principle
It is not always necessary to measure ocean currents directly. Sometimes the volume transport, the most important aspect of a current, can be inferred by applying a rule called the continuity principle. This rule states, in effect, that ‘what comes in must go out’. We will illustrate this principle by applying it to the flows in and out of the Mediterranean Sea through the Strait of Gibraltar.
The Mediterranean straddles latitude 30° N and in general in this area, evaporation exceeds precipitation and run-off from rivers. There is thus a net loss of fresh water from the Mediterranean Sea. The evaporation rate is about 1 metre each year, that is the surface of a pool of water that is not topped up with a hosepipe will fall by 1 m year–1. The surface area of the Mediterranean is about 2.5 million km2. The volume of water lost by evaporation in one year is the product of these two figures, namely 2.5 × 1012 m3 year–1, or 100,000 m3 s–1, or about 0.1 Sv. Since this water is lost, it must be replaced (otherwise the Mediterranean would eventually dry out, which it shows no signs of doing). The major connection between the Mediterranean and the rest of the world ocean is through the Strait of Gibraltar. The water lost by evaporation can therefore be replaced by a flow, equal to 0.1 Sv, through the Strait of Gibraltar.
The Strait of Gibraltar is 10 km wide and about 250 m deep at its narrowest and shallowest section, which gives a cross-sectional area of 2,500,000 m2. A flow of 0.1 Sv through a channel of this area will have a speed 100,000/2,500,000 = 0.04 m s–1 = 4 cm s–1. So the flow we might expect is quite slow.
However, it’s not as simple as this, because the flow in through the strait comes from the Atlantic and is salty, whereas the water that is lost by evaporation is fresh.
If you replace fresh water by salt water, the Mediterranean will get saltier with time. Again, there is no evidence that this is happening, so there must be some way in which the Mediterranean Sea is getting rid of salt. It does this with a deep flow of extra salty water through the Strait of Gibraltar. Observations in the narrowest section of the strait (Figure 4.5) show that the surface water has a salinity of about 37 and is flowing in. Below this, there is a layer of saltier water, with a salinity of about 38, which is flowing out. We can apply the principle of continuity to the salt as well as the water. This gives us two simultaneous equations for the inflow and outflow. When these are solved (see text box and Figure 4.6 for details), we learn that, in order to preserve the salinity and the volume of water in the Mediterranean, the inflow must be 3.8 Sv and the outflow 3.7 Sv.

Figure 4.5 Salinity section through the Strait of Gibraltar from North Africa to Spain. The high salinity water at the bottom of the strait is Mediterranean outflow water flowing towards the Atlantic underneath a layer of less salty Atlantic water flowing into the Mediterranean Sea.
Notice that, because of the requirement to maintain a salt balance, the flow rates are now much greater – in fact the volume flow in is 38 times greater. Because the cross-sectional area of the flow is also now only half the cross section of the strait instead of the full cross section (the outflow occupies the other half), the speed of the flow is over 70 times greater, or nearly 3 m s–1, or 6 knots. This is a considerable speed, and explains why sailing ships needed a fair wind to sail out of the Mediterranean against such a current.
Calculating flows in the Strait of Gibraltar using the continuity principle
The equations used to calculate flow rates by specifying conservation of salt and water are known as Knudsen’s equations after the Danish physicist Martin Knudsen. To see how they work, suppose the volume flow rate into the Mediterranean is FIN (units m3/s), and let the volume flow rate out be FOUT m3/s. Then the difference between these two must account for the loss by evaporation. The flow in must be a little bigger than the flow out. In fact, since the loss by evaporation, as we have seen, is 0.1 Sv,
FIN – FOUT = 0.1 Sv for a water balance

Figure 4.6 Sketch of the flows in the strait of Gibraltar. Atlantic water, of salinity about 37, is flowing towards you at the surface (circle with dot at centre). Mediterranean water, with salinity about 38, is flowing away from you (circle with cross).
A flow of FIN m3/s of linity 37 will carry salt at a rate 37 x FIN kg s–1 (since the salinity is the number of kg of salt per cubic metre of water). To maintain the salt balance, we would like the difference between the salt flowing in and that flowing out to be zero. That is:
37 × FIN – 38 × FOUT = 0 for a salt balance
These are two simultaneous equations for FIN and FOUT. The solution is obtained by dividing the second equation throughout by 37 and subtracting it from the first equation. This gives:
FOUT = 3.7 Sv
FIN = 3.6 Sv
In looking at Figure 4.5 you will notice that the interface between the inflowing Atlantic water and the outflowing Mediterranean water is not horizontal but slopes up towards Spain. The reason for this is that the flows are affected by the spin of the earth, which produces a phenomenon called the Coriolis effect (see next section).
4.4 The Coriolis effect
Soon after the invention of the barometer, it was discovered that winds, rather surprisingly, did not blow directly from high to low atmospheric pressure, but tended to follow isobars (i.e. blow along lines of constant pressure). The rule is that if you face into the wind in the northern hemisphere, the high pressure is to your left and low pressure to your right. This behaviour arises because we live on a spinning earth, and is called the Coriolis effect. The wind starts to blow from high to low pressure but is deflected to the right (in the northern hemisphere) because of the earth’s spin. Moving objects in the southern hemisphere are deflected to the left. Sometimes we imagine that there is a force – the Coriolis force – acting to the right of moving objects in the northern hemisphere, and to the left in the southern.
The Coriolis effect occurs because the surface of the earth is moving at different speeds at different latitudes. Perhaps the easiest way to envisage it is to imagine you are looking down on the earth from above the North Pole. The earth will be turning below you in an anticlockwise sense. A point on the Equator is moving eastwards at a little over 1610 km h–1. A point at 60° N (the latitude of the Shetland Isles) is moving eastwards at 805 km h–1. A point at the North Pole is not moving at all: a person standing there would simply turn to face different directions as the earth turns, but would have no velocity.
Now imagine you travel from the Equator towards the North Pole. Because you start from the Equator, you will have a speed of over 1610 km h–1 towards the east. Let’s say there is not much friction between you and the solid earth below you, so you keep this initial speed as you move around. This idea of little friction with the solid earth is probably true of surface ocean currents or winds in the higher parts of the atmosphere. As you travel northwards you will move over places that are not moving as fast to the east as you are. So, compared to the solid earth, you will appear to be deflected towards the east. By the time you arrive at the Shetlands, you will be travelling at 805 km h–1 towards the east from the point of view of someone standing on the Shetland Islands.
Ocean currents feel the Coriolis effect and are deflected by the Earth’s spin. Although the account we have given is for a current moving northwards, the same is true for currents moving in any direction; they are always deflected towards the right in the northern hemisphere and to the left in the southern hemisphere.
Many ocean currents and winds are driven by pressure differences, that is they flow (or, in the case of winds, blow) from high pressure to low pressure. As they do so, they turn to the right (in the northern hemisphere) because of the Earth’s spin. As a result they never actually get to the low pressure, but start circling round the high pressure. This effect is most familiar in the atmosphere, where winds circulate around a high pressure in a clockwise sense in the northern hemisphere. We say that the wind is in geostrophic balance: as it travels around the high pressure, the pressure force acts outwards (towards the left, looking downwind) and the Coriolis force acts inwards (to the right, looking downwind). The two forces are in balance, and the wind can blow in steady state, that is at constant speed, with a zero net force. Notice that zero force does not mean zero motion. According to Newton’s Laws, forces are required to produce accelerations. If there is no force there is no acceleration, but constant speed is perfectly acceptable. The geostrophic balance ignores frictional forces (see Figure 4.7).

Figure 4.7 Force balance in winds circulating around a high pressure system in the northern hemisphere. The winds blow around the high pressure in a clockwise sense. The pressure gradient force (PGF) acts outwards, from high to low pressure, and is balanced by the Coriolis force acting towards the right of the wind direction. The balance between pressure gradient and Earth rotation effects is important in both meteorology and oceanography and is called a geostrophic balance.
If water is confined to flow along a sea strait, the Coriolis effect tends to pile the water up against one shore – the shore to the right looking down the direction of flow. The flows in the Strait of Gibraltar illustrate this effect nicely. The Atlantic water flowing into the Mediterranean experiences a Coriolis force to the right. This tends to pile up Atlantic water against the right hand shore (the African coast) creating a high pressure on this shore. There is then a pressure gradient force in the surface layer acting from the African shore towards Europe, and this just balances the Coriolis force acting in the opposite direction. To provide this pressure gradient force, the sea surface slopes up towards the African coast, but the slope is quite gentle, and cannot be seen with the eye. In the lower layer, the flow is in the opposite direction, the Coriolis force is again to the right, which is towards Europe. This piles outflowing Mediterranean water against the European shore, creating a high pressure in the bottom layer on this shore. The interface between the two layers therefore slopes up towards Europe. This slope is quite considerable and can be observed by measurements of salinity at different depths. The flows and forces in a cross section of the Strait of Gibraltar are shown in Figure 4.8.
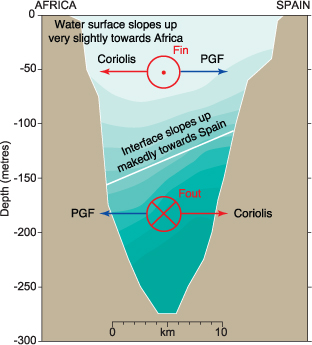
Figure 4.8 Geostrophic balance in the strait of Gibraltar. The Coriolis force on the outflowing Mediterranean water acts towards the right and pushes the Mediterranean water towards the Spanish side of the strait. This makes the interface slope up towards this side. The resulting pressure gradient force (PGF) then balances the Coriolis force in the bottom layer. In the upper layer, the Coriolis force pushes the flow towards the African shore, producing a sloping sea surface and a pressure gradient force acting from Africa towards Spain. The slope in the sea surface required to balance the Coriolis force in the upper layer is very gentle (of order 1 in 100,000) but the slope in the interface needs to be much greater than this because of the small density difference between the two layers.
As the Mediterranean water leaves the Strait of Gibraltar and enters the Atlantic Ocean, it cascades down the sloping seabed, flowing through colder and fresher Atlantic water, which is less dense than the Mediterranean water. As the Mediterranean outflow water tumbles down the sea floor, it mixes with the overlying Atlantic water, becoming less salty and therefore less dense. When it reaches a depth of about 1000 m, it reaches Atlantic water that is denser than itself, and it leaves the ocean floor and spreads out as a layer in the Atlantic. This layer of warm, salty water from the Mediterranean, at a depth of about 1000 m, can be detected throughout the north Atlantic, at great distances from the Strait of Gibraltar (see Chapter 1).