Poker has changed dramatically and quickly in the last few years. The game is much tougher than it used to be. Version 2.0 of the game is characterized by very high aggression, off-the-charts variance, and relentless pressure. This is not the same game I played back in the day, not at all.
In the old days, if you had good pre-flop fundamentals, you were a cinch to win. That is why most of the material written about the game (including my previous books) has focused on the pre-flop game. Now, most people play well pre-flop, but the edge comes from post-flop play. Post-flop is where the pros are separated from the posers.
Table composition has also changed dramatically. As late as 2007, I could easily find a nine-handed game with three, four, even five weak spots. These “fish” were easily fried, and you didn’t even have to be that good a fisherman to fill your quota. There was plenty of money to go around. These days, we’ve depleted the ocean, and fish are simply not as plentiful. Now, at a nine-handed table, there might only be one fish, and all the fishermen are fighting to get him on the line first.
Much of this change has been fueled by a rigorous scientific study of the game through simulation and mathematics. It is no longer good enough to know my Rule of 4 and 2. To really understand Poker 2.0, you need to get more comfortable with the math underlying this new playing style. If you are less mathematically gifted, don’t be intimidated—I have made this material as approachable and simple as possible.
“Range” is the set of all possible hands an opponent can have based on your knowledge of their playing style and all actions that have taken place during the play of a hand. A typical pre-flop range might sound something like this: “He’s on, at worst, any pocket pair, AJ offsuit,* or, better, KQ suited, or QJ suited.”
Poker players routinely use “range” when thinking about or discussing a hand:
PLAYER: He’s got a really wide range here.
TRANSLATION: He can be playing almost any two cards.
PLAYER: I’m at the top of my range.
TRANSLATION: Of the hands that my opponent suspects I could be playing, this hand is one of the best I could have.
PLAYER: He’s playing about 10% of his hands pre-flop from early position.
TRANSLATION: His range is pocket sevens or better, AT offsuit or better, A8 suited or better, KQ suited, QJ suited, and JT suited.
It is very important to think about an opponent’s range throughout the play of a hand. It is also vitally important that you consider what range of hands your opponent is putting you on.
Range analysis, often through computer simulation (and later, experience), has intensified and become one of the most important tools in NLH2.0—without it, you’ll have little or no chance to succeed. I’ll show you how to do these range analyses later in the book.
When writing about range, it is helpful to have a standardized notation. The Internet whiz kids quickly figured out a range notation that is very useful. Here is a quick rundown, via example:
Any pocket pair: 22+
Pocket nines or better, AJ or better (meaning AK, AQ, AJ), KJ suited or better (KQ, KJ): 99+, KJs+, AJ+
Top 20% of all possible hands: 20%+
Some 30% of all possible hands, but not AA or KK: 30%+ - KK+
A “very tight” under-the-gun range in a full No Limit Hold’em ring game: TT+, AQs+, AK
A “loose button-position” range: 22+, A2+, K2+, Q2+, J8+, J5s+, T9s, 85s+, 74s+, 63s+
Note: In all cases, a range of A2+ denotes all unsuited combinations and automatically includes all suited combinations as well. So, A2+ is the same as A2s+, A2o+. This is the notation I’ll be using throughout the rest of the book.
Position is extremely important. We need some common terminology and abbreviations to be able to talk about position intelligently. Refer to this chart for the names of certain seats with respect to the button. Also, I’ll be discussing 6-max games* quite a bit. When thinking about 6-max, I simply visualize a 9-player table where the UTG, UTG+1, and MP1 players have folded. In a 6-max game, the UTG position is the MP2 position at a full ring.
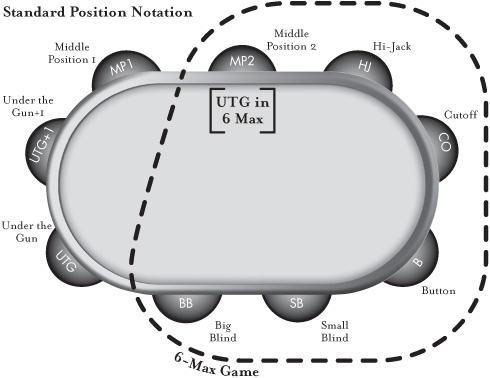
NLH2.0 is based largely on mathematics. Without the “reads” and “tells” commonly associated with live play, the Internet poker geniuses had no choice but to adapt and find other ways to win, and they focused most of their efforts on the mathematics of the game.
To understand and ultimately be successful in the new poker world, you’re going to have to expand your math repertoire beyond the basics of the Rule of 4 and 2 and Pot Odds. Your new weapons will include three concepts: combinatorics, expected value (EV), and combined probability. If you haven’t mastered simple pot odds calculations or you have a hard time figuring out your chances of winning after the flop or turn, go back and study my Green Book for a detailed explanation.
Combinatorics means listing all possible two-card combinations and then figuring out the likelihood of any given combination or range of combinations being dealt. Let’s start with the basics: There are 1,326 possible two-card starting hands in Texas Hold’em. How do we know that? Well, there are 52 cards in the deck. After you select a single card from the 52, there are 51 cards possible for your second hole card. So, the total number of combinations is: 52 × 51 = 2,652.
However, there is no difference if we’re dealt the Ace of Clubs first followed by the Seven of Diamonds or if we’re dealt the Seven of Diamonds first followed by the Ace of Clubs—it is the same hand. Clearly, each possible two-card combination has been counted twice.
So, the total number of two-card combinations in Texas Hold’em is: 2,652 ÷ 2 = 1,326.
Now, with that under our belts, let’s take a look at all the ways we can be dealt the best possible hand, AA: A♣A♦, A♣A♥, A♣A♠, A♦A♥, A♦A♠, A♥A♠.
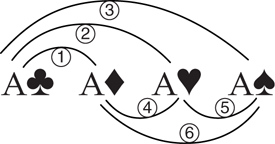
Of the 1,326 possible two-card starting hands, there are clearly six ways to be dealt AA, so the chances are: 6 ÷ 1,326 = 0.0045 = 0.45%.
Now, let’s move on to a slightly worse hand, Ace-King, either suited or unsuited.
There are sixteen ways to be dealt AK; four are suited, and twelve are unsuited. Indeed, there are sixteen ways to be dealt every unpaired hand. There are sixteen combinations of 7-2, sixteen combinations of QT, and sixteen combinations of 9-5. The probability of being dealt any specific unpaired hand like AK is:
16 ÷ 1,326 = 0.012 = 1.2%
With 1,326 combinations possible, every 13 combinations account for 1% of the possible hands, every 66 combinations represent 5% of the possible hands, every 132 combinations is equivalent to 10% of the hands, and so on.
These two basic combinatorics are the essential building blocks for advanced Poker 2.0 calculations. Now, let’s try a few examples …
Example 1:
What are the chances of being dealt a pocket pair?
13 different pairs (or ranks) × 6 combinations for each rank = 78
78 ÷ 1,326 = 0.0588 = 5.88%
What are the chances of being dealt a hand in the following range: 77+, ATs+, KQs, AQo+?
77–AA = 8 ranks × 6 combinations = 48
ATs+ = 4 kickers × 4 combinations = 16 (ATs, AJs, AQs, AKs)
KQs = 4 combinations (K♣Q♣, K♦Q♦, K♥Q♥, K♠Q♠)
AQo+ = 2 kickers (K, Q) × 12 combinations = 24 combinations
___________________________________
48 + 16 + 4 + 24 = 92 combinations
92 ÷ 1,326 = 0.0694 = 6.94%
Example 3:
What are the chances of being dealt a “suited” hand?
Ranks |
A |
K |
Q |
J |
T |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
|
Kickers |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
× Suits |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
|
= Total |
48 |
44 |
40 |
36 |
32 |
28 |
24 |
20 |
16 |
12 |
8 |
4 |
= 312 |
312 total combinations ÷ 1,326 = 23.5%
Example 4:
If we think our opponent is playing 12% of their hands from under the gun, how many combinations does that represent?
1,326 × 12% = 159.12 ≈ 159 combinations
If an opponent is playing all pocket pairs and is playing 12% of his hands from under the gun, how often will he be unpaired?
12% range = 159 combinations (see Example 4)
From Example 1, we know that there are 78 pair combinations.
159 − 78 = 81 unpaired hands
81 unpaired combinations ÷ 159 total combinations = 0.509 = 50.9%
Our opponent will be unpaired a little more than half the time.
At first blush, 1,326 looks like the magic number for poker combinatorics. It certainly is when evaluating your hand or range of hands. But, as you well know, more often than not what we’re more concerned about is the possible hands our opponents can hold. That means we need to make some minor adjustments to our calculations.
After you look at your hole cards, you have some vital information: your opponent can’t be dealt either of the two cards you hold in your hand. There are 50 cards left in the deck. That means that the number of remaining two-card combinations decreases from 1,326 to 1,225.
50 × 49 ÷ 2 = 1,225
Obviously, the possibilities for your opponent’s hand are affected after the removal of your known hole cards from the deck. Intuitively, you know that if you have an Ace in your hand, it is much less likely that any one of your opponents will be dealt one as well. Let’s take a look at a few examples:
Example 1:
You are dealt A♥Q♠. What are the chances that your opponent was dealt AA?
3 combinations of AA ÷ 1,225 = 0.0024 = 0.24%
(Notice that by being dealt an Ace, thereby removing it from the deck, the number of combinations of AA decreases by 50%—there are six combinations of AA if you don’t have an Ace in your hand, three if you do: A♣A♦, A♣A♠, A♦A♠.)
Example 2:
You have A♠K♠. What are the chances that a single opponent has AA or KK?
As we learned above, once the A♠ and K♠ have been dealt to you, your opponent’s chance of having either pocket pair is cut in half.
AA, KK = 3 combinations each = 6 combinations total
6 ÷ 1,225 = 0.0048 = 0.48% or about 1 out of 204
You’re in the small blind with A♣2♣. What are the chances that your opponent in the big blind has a better hand (pocket 22+, A3−AK)?
Well, you’re in the lead against all non-pair, non-Ace hands, which are easy to count.
22, AA = 3 combinations each = 6 combinations
33−KK = 6 combinations each × 11 ranks = 66 combinations
A3−AK = 12 combinations of each × 11 ranks = 132 combinations (3 remaining Aces combined with 4 of each kicker)
6 + 66 + 132 = 204 combinations ÷ 1,225 = 16.65%
Example 4:
Your opponent has a hand in the following range: 88+, ATs+, AQo+, KQs, QJs, JTs
You are dealt QQ. What are the chances that you have the best hand right now?
First, we’ll count the combinations in our opponent’s range that have us beat:
AA, KK = 6 combinations each = 12 combinations beat us
Now, let’s count the other combinations in the range:
88−JJ = 6 combinations of each × 4 ranks = 24 combinations
ATs, AJs, AKs = 12 combinations
AQs = 2 combinations (2 queens gone)
AQo = 6 combinations (2 queens gone)
AKo = 12 combinations
KQs = 2 combinations (2 queens gone)
QJs = 2 combinations (2 queens gone)
JTs = 4 combinations
__________________________________
24 + 1 + 12 + 2 + 6 + 12 + 2 + 2 + 4 =
65 combinations we are ahead against
We beat 53 of the 65 combinations: 53 ÷ 65 = 0.815 = 81.5%
With QQ vs. this range, we expect to be “ahead” 81.5% of the time.
Expected Value (EV) is a term from probability theory with a splash of economics. Essentially, EV is a probabilistically weighted average of all possible outcomes. You can think of EV as the “long-term outcome” of a play.
First, an example where you have nothing to lose (unfortunately, these situations don’t come up often in poker):
There is $100 in the pot, and you compute that you have a 60% chance of winning. What is your EV?
Answer:
60% of the time, you’ll win $100. 40% of the time, you’ll win $0.
$100 × 60% = $60
+ $0 × 40% = $ 0
__________________
EV = $60
Over the long run, you can expect to win $60.
Example 2:
I have three piggy banks. Piggy bank A has $50 in it. Piggy bank B has $100 in it. Piggy bank C has $1,000 in it. You randomly select a bank and get to keep whatever you find. What is your EV?
Answer:
33% of the time, you’ll choose Piggy A and get $50
33% of the time, you’ll choose Piggy B and get $100
33% of the time, you’ll choose Piggy C and get $1,000
33.3% × |
50 = $ 16.67 |
33.3% × |
100 = $ 33.33 |
+33.3% × |
1,000 = $333.33 |
|
EV = $383.33 |
If you played this game thousands of times, you’d expect to win, an average of $383.33 each time.
Example 3:
You bet $250 on the LA Lakers to win the NBA championship with your best friend. You think you have a 52% chance of winning that bet. What is your EV?
Answer:
52% of the time, you’ll win $250.
48% of the time, you’ll lose $250.
52% × $250 = |
$130 ← You win |
+48% × −$250 = |
−$120 ← You lose |
__________________________ |
|
EV = |
$ 10 |
On average, this bet is worth $10. In other words, you are risking $250 for the expectation of winning $10 over the long run.
Example 4:
You are heads up at the river and your opponent bets $700 into a $1,000 pot. You can beat a bluff, but only a bluff. What percent of the time must your opponent be bluffing to make this a profitable call?
Answer:
If he has the best hand, you will lose $700. If he was bluffing and you have the best hand, you will win $1,700, the $1,000 in the pot before his bet plus the $700 bluff.
The key now is to determine the Break Even Percentage (BEP):
Let B = the percent chance that he is bluffing
So, 100% − B = the percent chance that he has the best hand and we lose
We are searching for the equilibrium point where:
0 = EV(winning) + EV(losing)
EV(winning) = 1,700 × B
EV(losing) = −700 × (100% − B)
Now, time for some algebra:
0 = (1,700 × B) −700 + (700 × B)
0 = (2,400B) − 700
700 = 2,400 × B
700 ÷ 2,400 = B
0.292 = B
29.2% = B
What this shows us is that if our opponent is bluffing 29.2% of the time and we call each and every time, we will break even over the long run.
Quick double-check:
29.2% × $1,700 = |
$496 ← EV of catching a bluff |
+70.8% ×− $700 = |
−$496 ← EV of losing |
__________________________ | |
EV = |
0 |
Since this situation comes up so much, it is useful to generalize the BEP formula like this:
BEP = Amount of Bet ÷ Total Pot, including my call
So, let’s try a few more of these river situations and apply the BEP formula:
Example 4a:
Pot is $500, opponent bets $500. What percent chance do you need to justify a call?
River Bet = $500
Total Pot if I call = $1,500
BEP = $500÷$1,500 = 33%
Example 4b:
Pot is $10,000. River Bet is $1,000. What percent chance do you need to justify a call?
River Bet = $1,000
Total Pot if I call = $12,000
BEP = $1,000÷$12,000 = 1÷12 = 0.125 = 12.5%
We’ll see BEP in action in later sections. If these formulas make your head spin, here is a chart of river bet sizes and the associated BEP:
River Bet Size
1/2 pot - 25% BEP
3/4 pot - 30% BEP
POT - 33% BEP
1.5x pot - 37.5% BEP
2x pot - 40% BEP
Putting EV together with Combinatorics
A player moves all-in pre-flop for $100. Like Phil
Hellmuth, you look deep into their soul and know that they have AA or AK. You have QQ. Should you call?
There are 6 combinations of AA. If they have AA, you’re going to suck-out and win about 18.5% of the time and lose about 81.5% of the time.*
There are 16 combinations of AK. If they have AK, you’re going to win about 56% of the time.
So, there are 22 total combinations to consider:
AA, Suck-out (6 / 22) × 18.5% × +$100 = |
$5.04 |
AA, Lose (6 / 22) × 81.5% × −$100 |
= −$22.28 |
AK, Win (16/22) × 56.0% × +$100 |
= $40.73 |
AK, Lose (16/22) × 44% × −$100 |
= −$32.00 |
___________________________________________________________ |
|
EV = |
−$8.51 |
Remember, this is weighted probability. For this situation if you decide to call in this spot, you are essentially “giving” your opponent $8.51. You should not call.
Players in Poker 2.0 are always thinking about EV. If they believe a play has a positive EV, they make the play. They know that at “Internet speed,” they’ll get to make that same play thousands of times, and over the long run, they’ll be big winners.
One key concept about EV worth noting: the results of any one particular hand aren’t all that important. If you have AK and get it all-in against QQ and win the hand, that is excellent in the short term—you doubled up! But, if you keep doing the same thing over and over and over, you’ll end up broke—your opponent is getting the best of every hand a little bit at a time. Bottom line: getting lucky doesn’t mean that you played well.
I’m in the cutoff seat (just to the right of the button) and I’m thinking about moving all-in for my last 12 big blinds with A♠T♣. I’d like to figure out how often I’m going to get called by a dominating hand (AJ, AQ, AK, TT, JJ, QQ, KK, AA) by one of three players remaining. Here, I need to use combinatorics and approach the problem as if there were a single player left to act:
3 Aces are left in the deck.
AJ, AQ, AK = 12 combinations of each = 36 total combinations
AA, TT = 3 combinations each = 6 combinations
KK, QQ, JJ = 6 combinations each = 18 combinations
_______________________________________
A total of 60 combinations have me dominated.
As I’ve shown, after my A♠T♣ have been removed from the deck, there are 1,225 possible combinations (50 3 49 4 2) for my opponent.
60 dominant combos 4 1,225 total combos = 0.0489 = 4.89% chance I’m dominated.
100% − 4.89% = 95.11% chance I’m not dominated by a single player.
So, there is a 95% chance I’m not dominated by the button, a 95% chance I’m not dominated by the small blind, and a 95% chance I’m not dominated by the big blind. We combine these probabilities by multiplying them all together:
95% 3 95% 3 95% = 85.7% chance I’m not dominated by any of the remaining three players.
Example 1:
You own two stocks. You estimate a 10% chance the price of Stock A will increase. You estimate a 30% chance the price of Stock B will increase. What is the probability of both stocks increasing?
10% chance Stock A increases × 30% chance Stock B increases = 0.10 × 0.30 = 0.03 = 3%
Example 2:
You purchase a “parlay” card at the sports book. You have to pick three games correctly in order to win. You are an excellent handicapper and believe that you have a 55% chance of picking Game A correctly, a 52% chance of picking Game B correctly, and a 59% chance of picking Game C correctly. What is the probability that you’ll win the parlay?
55% × 52% × 59% = 0.168 = 16.8%
Combined probabilities are very useful in multi-way pots and in all spots where there are multiple players left to act. In general, be more careful and conservative when there are multiple players left to act.
Utility is the measure of how important an outcome is to an individual player. For some, there is a substantial difference between coming in fifth place and cashing for $3,000 and coming in fourth place for $4,500. Some might place great importance on winning the extra $1,500, while others will find very little value or utility in the extra money.
Here’s a typical utility problem, as seen every day on the show Deal or No Deal. Suppose you’re in deep on the show with two choices remaining on the board. One box contains $10 and the other box has $250,000 in it. The banker offers to settle with you for $100,000. Deal or No Deal?
The expected value for just choosing a box is about $125,000. If you take the deal, you are essentially giving away $25,000 in expectation. Clearly, if you could get in this spot thousands of times, you’d just keep picking boxes and would never settle for $100,000. But, this is your only shot. The problem you face is simple: is the guaranteed usefulness of $100,000 worth giving up $25,000 in expectation? Many people, myself included, would probably just take the $100,000 and give Howie Mandel a hug.
Now, suppose the remaining two boxes contained $90,000 and $130,000 and the banker offered $100,000. The expected value is $110,000, but I suspect that not many people would take the deal—there simply isn’t much of a difference between the utility of the $90,000 minimum and the $100,000 offer. The usefulness of the guaranteed extra $10,000 won’t be enough to convince many people to give up the chance at an extra $30,000 for a total of $130,000.
Understanding utility and how it affects decision making at the poker table is critical. There are many utility points, and many are exploitable. Here are some of the more common spots:
Near the end of a tournament day. The utility of “making Day 2” in a big tournament is important to some players, a milestone worthy of bragging rights. You can often get them to lay down big hands or expect them to play very tight near the end of the day.
Near the bubble in a tournament. On the bubble, many players, especially satellite winners, believe that cashing, even for the minimum, is the most important thing they can do. The utility for getting in the money can make them do some crazy, mostly nitty things.
Moving up a place in a tournament. In many tournaments, the difference in prize money between rankings can become quite substantial. Suppose 4th place pays $50,000 and 3rd place pays $100,000. For many, many players, that extra $50,000 is extremely important, and they will play a strategy counter to pure expectation in order to secure the utility of that extra $50,000. Usually, they will play tighter than they should from a pure EV perspective.
Protecting winnings in cash games. If I’m playing in a $1–$2 cash game and I know that a guy is up $800, I know he will be cautious about dipping below his initial buy-in of $200. The utility of being a “winner” in the game is more important to him than making a winning decision in the current hand.
Players who base their decisions on utility instead of expected value aren’t necessarily making a mistake. Yes, they are making an expected-value error. But that doesn’t mean they are making a mistake with respect to their life goals. If a guy owes $20,000 in credit card debt and is folding every hand on the bubble to make enough money to get out of debt, who are we to say that he’s making a mistake by folding Aces? Perhaps the utility of being out of debt is more important to him than maximizing his expectation. Expected value is objective, while utility is subjective and personal.
No, this isn’t some kind of Latin conjugation exercise. These terms come from the branch of mathematics called “game theory” and, as you might expect, they are very important in poker, particularly in “the game” of Poker 2.0.
In game theory, a “strategy” is a plan of attack, a method of play, or your game plan. A strategy is said to be “exploitable” if an opponent can implement a counterstrategy that is certain to triumph in the long run. A strategy is said to be “unexploitable” if there is no strategy that an opponent can come up with to beat it over time.
To simplify it, let’s see this concept in the context of Roshambo, or Rock-Paper-Scissors. In Roshambo, say you’re playing against a “Bureaucrat” who only knows one move: paper. Obviously, this is an exploitable strategy—all you have to do to win is always go scissors.
A slightly more sophisticated player randomly decides to go either paper or scissors. Again, this strategy is easily exploitable. You simply always go scissors—you will either tie or win and you’ll never lose.
In Roshambo, an unexploitable strategy is to go completely random with your throws. Over time, a random strategy will break even—there is no exploitative strategy that a player can implement to counter and get the best of a random strategy.
In poker, there are two basic approaches: you’re trying to play either an unexploitable strategy or an exploitative strategy (which, in turn, will probably make you exploitable).
An exploitative strategy seeks out holes and weaknesses in an opponent’s strategy and then counters with the highest possible EV play. Below are some clear-cut exploitable strategies and their associated exploitative counterstrategies that will crush.
Exploitable Strategy |
Exploitative Counterstrategy |
Wait for Aces |
Play every hand and steal like a bandit |
Raise with strong hands, limp with weak hands |
Fold when they raise, raise when they limp |
Never bluff |
Fold when they bet or raise |
Go all-in every hand |
Wait for the nuts |
Bluff too much |
Call with more bluff-catchers |
I love to watch great tennis players battle on the court. Take a classic pairing that almost always produces an awesome, strategic battle: Roger Federer vs. Rafael Nadal. Nadal has what is probably the best forehand in tennis, while Federer has an absolutely deadly backhand. For each of them, there is a better chance that they will win the point on any given shot if they hit a shot to their opponent’s weakest side: Nadal tries to hit shots to Federer’s forehand and Federer wants to hit shots to Nadal’s backhand. Accurate as these guys are, it is no surprise that matches between them feature an alarmingly large number of Federer forehands and Nadal backhands.
They each know their opponent’s strategy—this is where “balance” enters the game and makes things very interesting. See, in order to catch their opponent off guard, occasionally, they have to hit a ball to his stronger side. By mixing their strategies, they prevent their opponent from accurately anticipating where the next shot will be placed. Although the chances of them winning a particular point decreases substantially on that particular stroke (because they are hitting to the strong side), the overall chance of winning the point increases dramatically because they keep their opponent guessing.
In poker, balancing the range of hands you play and the way you play them is important—you simply must keep your opponent guessing. Most of the time, you play a hand in the most profitable way possible, but occasionally, you should mix it up and deviate from the “normal” line of play to make your overall game more profitable. In most cases, there is a “best play” available for a particular situation. Using experience, reads, game flow, and some randomness to deviate from the normal, best play will make you much, much tougher to read and a much stronger player.
In order to explain the merits and principles of balance, I want to walk you through a simple game. Let’s say there is $100 in the pot. Half the time (50%) your opponent has the nuts (and you’ll lose), and the other half of the time (50%) he has air (and you’ll win). Your opponent has the option of betting $100 or checking.
One unbalanced strategy your opponent might use would be to always bet the nuts and always check with air. You can counter that strategy by always folding if they bet. That should be clear—calling a bet if they always have the nuts is suicidal. By adopting this strategy, you will play the game absolutely perfectly against this opponent.
Now, let’s say the villain complicates life a little and implements another unbalanced strategy—betting every single hand. What is your best counterstrategy? Well, if you call every single hand, 50% of the time (they were bluffing) you’ll win $200 ($100 in the pot and the $100 bet) and 50% of the time you’ll lose the $100 bet (they had the nuts), for an expected value of $50 per hand. Clearly, if they bet every single hand, calling every bet is correct and will show the highest profit.
A balanced strategy for our opponent requires that he bet every good hand and some bad hands—his best strategy is to keep us guessing. Let’s see what happens if he bets all his good hands and half of his bad hands, and we call every bet.
What should be clear is that he’s bluffing one-third of the time when he bets the river. He’s betting all of his good hands (50%) and half of his bad hands (25%). Overall, he’s betting 75% of the time, and 25% of those bets are bluffs. 25% ÷ 75% = 33.3%. So, if he’s bluffing 33% of the time, he has the nuts 66.6% of the time.
Expected Value:
66% × −100 = −66.66
33% × +200 = +66.66
_______________________________
= 0
By bluffing one-third of the time, he essentially gives us no way to “win” on the river. We can call every single time and the best we can do is break even. This balanced strategy is said to be unexploitable.
Balance is overused, in general, except against the very best players. Bad players tend to make bad mistakes, and they don’t adjust their strategy, so with them you don’t need to balance your game. Think about it this way: should you ever bluff on the river against a guy who is going to call every bet? Of course not! Bluffing against players who won’t and can’t fold is moronic. They are going to call! You don’t need to balance your river play against this type of opponent—in fact, doing so will cost you dearly. Against this type of opponent, you simply bet everything that will beat 50% of their range and check everything else. That should be obvious, and yet, it is a mistake that I see world-class players making all the time. You simply can’t bluff someone who is incapable of folding.
Use a balanced strategy against the best players, and just play an exploitative game against the rest. As I said in my Green Book, 90% of the money you win at the table will come from the few bad players. Bottom line: strive to play an unexploitable, balanced strategy against the great players, and a straightforward exploitative strategy against the weak players.
