Parameterization of HMM

In the previous section, we saw an example of an HMM to get an idea of how the model works. Let's now formally parameterize an HMM.

As the latent variables of an HMM are discrete multinomial variables, we can use the 1-of-K encoding scheme to represent it, where the z_n variable is represented by a K-dimensional vector of binary variables, z_nk ∈ {0,1}, such that z_nk = 1 and z_nj = 0 for j ≠ k if the z_n variable is in the k state.

With this in mind, we can create a matrix with the transition probability matrix A, where A_ij = Pr(Z_nj = 1| z_n-1, i = 1). As the A_ij represent the probability of moving from state i to state j, it holds the property of 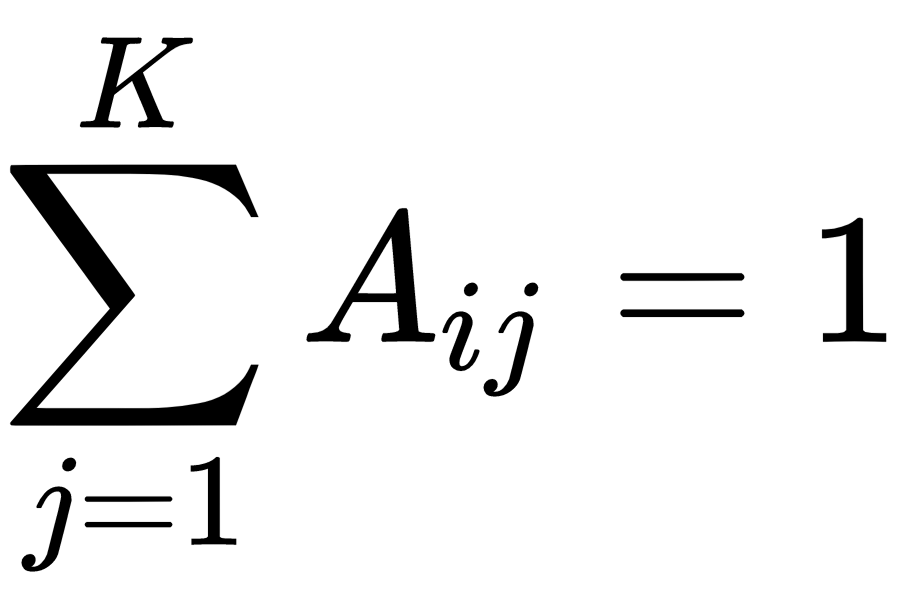 and can be expressed using the K(K-1) parameters. Thus we can represent the conditional probability distribution as follows:

The transition matrix is generally represented using a state-transition diagram, as we saw in Chapter 1, Introduction to Markov Process. But we can take the same representation and unfold it across time to get a lattice or trellis diagram, as presented in the following image. We will be using this representation of HMM in the following sections for learning parameters and making inferences from the model:

Trellis diagram for an HMM with latent variables with three states

As the initial latent node, z₁, does not have a parent node, it has a marginal distribution, Pr(z₁), which can be represented by a vector of probabilities, π, such that π_k = Pr(z_1k = 1) with . Thus, the probability of Pr(z₁|π) can be expressed as follows:

The third and final parameter required to parameterize an HMM is the conditional probability of the observed variable given the latent variable, namely the emission probability. It is represented by the conditional distribution, Pr(x_n| z_n, Φ), which is governed by some parameters, Φ. If the observed variable, x_n, is discrete, the emission probability may take the form of a conditional probability table (multinomial HMM). Similarly, if the observed variable, x_n, is continuous, then this distribution might be a Gaussian distribution (Gaussian HMM) where  denotes the set of parameters governing the distribution, namely the mean and variance. 

Thus, the joint probability distribution over both the latent and observed variables can be stated as follows:

Here, X = {x₁, ..., x_N}, Z = {z₁, ..., z_N} and θ = {A, π, Φ} denotes the set of parameters governing the model.

An HMM model is called a homogenous model when all the conditional distributions governing the latent variables share the same transition matrix, A, and all the emission probabilities share the same parameters, Φ. 

Now, let's try to code a simple multinomial HMM. We will start by defining a simple MultinomialHMM class and keep on adding methods as we move forward:

import numpy as np

class MultinomialHMM:
 def __init__(self, num_states, observation_states, prior_probabilities,
 transition_matrix, emission_probabilities):
 """
 Initialize Hidden Markov Model

 Parameters
 -----------
 num_states: int
 Number of states of latent variable
 observation_states: 1-D array
 An array representing the set of all observations
 prior_probabilities: 1-D array
 An array representing the prior probabilities of all the states
 of latent variable
        transition_matrix: 2-D array
            A matrix representing the transition probabilities of change of
            state of latent variable
        emission_probabilities: 2-D array
            A matrix representing the probability of a given observation
            given the state of the latent variable
        """
        # As latent variables form a Markov chain, we can use
        # use the previous defined MarkovChain class to create it
        self.latent_variable_markov_chain = MarkovChain(
            transition_matrix=transition_matrix,
            states=['z{index}'.format(index=index) for index in range(num_states)],
        )
        self.observation_states = observation_states
        self.prior_probabilities = np.atleast_1d(prior_probabilities)
        self.transition_matrix = np.atleast_2d(transition_matrix)
        self.emission_probabilities = np.atleast_2d(emission_probabilities)

Using the MultinomialHMM class, we can define the HMM coin that we discussed previously as follows:

coin_hmm = MultinomialHMM(num_states=2,
                          observation_states=['H', 'T'],
                          prior_probabilities=[0.5, 0.5],
                          transition_matrix=[[0.5, 0.5], [0.5, 0.5]],
                          emission_probabilities=[[0.8, 0.2], [0.3, 0.7]])