The Viterbi learning algorithm (not to be confused with the Viterbi algorithm for state estimation) takes a set of training observations Or, with 1≤r≤R, and estimates the parameters of a single HMM by iteratively computing Viterbi alignments. When used to initialize a new HMM, the Viterbi segmentation is replaced by a uniform segmentation (that is, each training observation is divided into N equal segments) for the first iteration.
Other than the first iteration on a new model, each training sequence O is segmented using a state alignment procedure which results from maximizing:
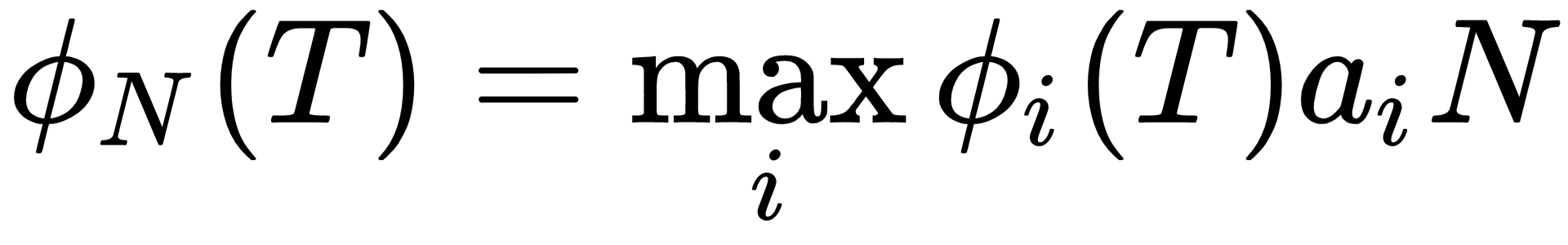
for 1<i<N where:
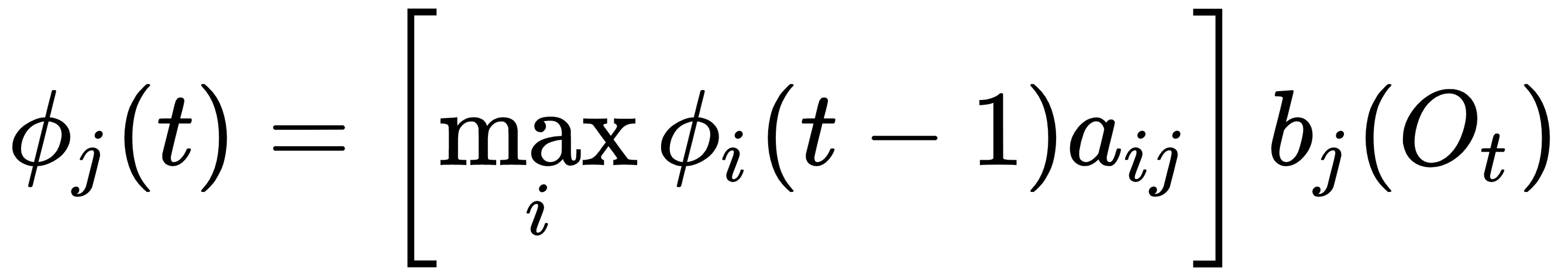
And the initial conditions are given by:
for 1<j<N. And, in the discrete case, the output probability 
is defined as:
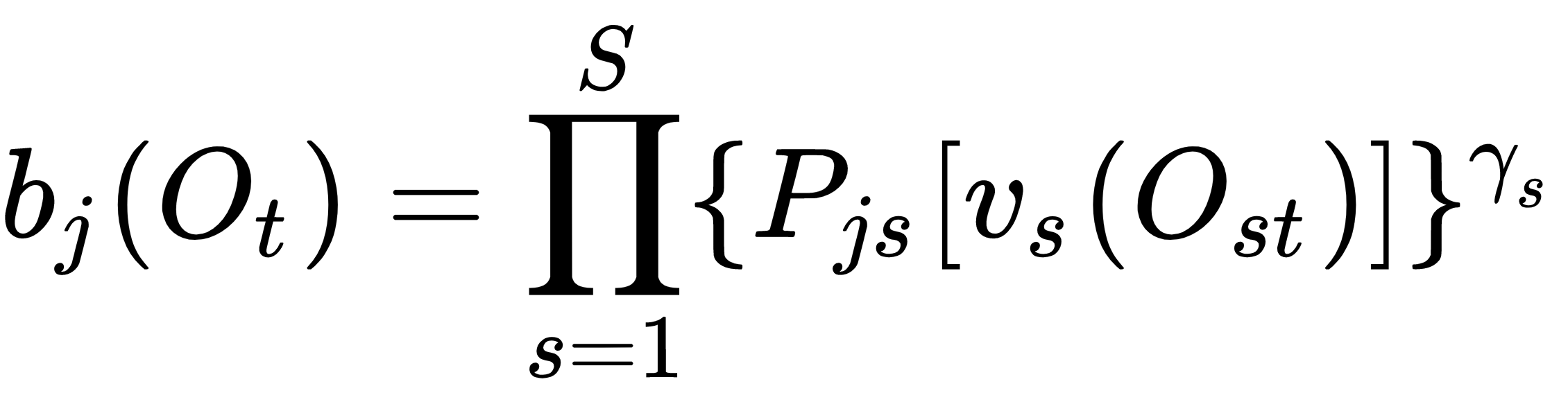
where S is the total number of streams, vs(Ost) is the output given, the input Ost, and Pjs[v] is the probability of state j to give an output v.
If Aij represents the total number of transitions from state i to state j in performing the preceding maximizations, then the transition probabilities can be estimated from the relative frequencies:
The sequence of states that maximizes ∅N(T) implies an alignment of training data observations with states. Within each state, a further alignment of observations to mixture components is made. Usually, two mechanisms can be used for this, for each state and each output stream:
- Use clustering to allocate each observation Ost to one of Ms clusters
- Associate each observation Ost with the mixture component with the highest probability
In either case, the net result is that every observation is associated with a single unique mixture component. This association can be represented by the indicator function 
, which is 1 if 
is associated with a mixture component m of stream s of state j, and is zero otherwise.
The means and variances are then estimated by computing simple means:
And the mixture weights are based on the number of observations allocated to each component:
