Tree-structured HMM

In the previous section, we discussed factorial HMM, in which the latent variables formed independent Markov chains. This independence assumption about the latent variables can be relaxed by introducing some coupling between them. One way to couple latent variables is to order them such that 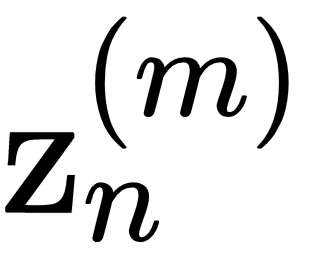 depends on  for all 1 ≤ l ≤ m. Furthermore, if all the output variables and the latent variables depend on some random input variable, x_n, we obtain a tree-structured HMM represented as follows:

Graphical representation of a tree-structured HMM

The architecture of this model can be interpreted as a probabilistic decision tree. Let's considered at first-time slice n=1, and try to understand how this model would generate data. Based on the value of x₁, the top node, 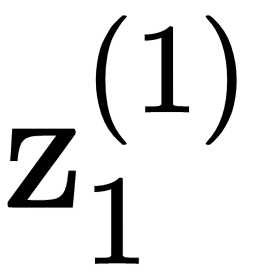, can take K values (assuming that the hidden variables have K states). This partitions the x space into K decision groups. The next node, 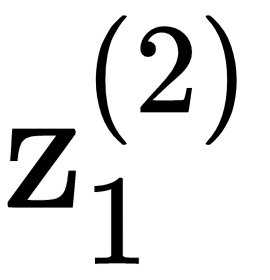, further partitions into K subregions, and so on. The output, y₁, is generated from the input, x₁, and K-way decisions at each node. At the next time slice, the same thing is going to happen, expect that each decision in the tree depends on the decision taken at that node in the previous time slice. Therefore, this model can be interpreted as a probabilistic decision tree with Markovian dynamics.