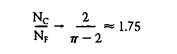
from:
Robert Wentworth,
September 21, 1984
DEAR MR DELANY,
I thoroughly enjoyed your novel, Neveryóna, which I just finished reading. I wonder, however, if you would forgive my pointing out a few mathematical inaccuracies in your discussion of Venn’s solution to ‘Belham’s Problem.’
My interest was piqued when I read about Venn’s proposed method in Chapter 12 for determining π. I was sure that I had heard of the method before, but I never understood why it worked. So, I sat down and did some mathematical analysis to convince myself that one can estimate π by tossing a stick onto a sheet of paper ruled with parallel lines spaced a stick-length apart. The mathematics told me that, yes, the results of this experiment can be used to estimate π but that the correct method is not quite as you have described.
In particular, if you divide the number of times that the stick crosses a line (Nc) by the number of times that the stick lies free (NF),
you find that the results get nearer and nearer 2/π-2, the more times you toss:
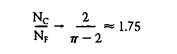
(The arrow means ‘approaches’ and the wavey equals sign means ‘approximately equals.’) Thus Nc/NF does not directly give an estimate of π. You could of course estimate π from 2 + 2/(Nc/NF) but it is simpler to estimate π by multiplying the total number of tosses (N) by two and dividing this by Nc. This ratio does approach n as the number of tosses gets larger and larger;
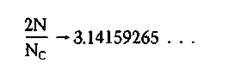
On page 356 of the first, mass market edition of Neveryóna, Venn says: ‘If you throw down the stick repeatedly, and if you keep count of the times it falls touching or crossing a line, and if you keep count as well of the times it lands between lines, touching or crossing none of them, and if you then divide the number of times it touches or crosses a line by the number of times it lies free, the successive numbers that you express, as you make more and more tosses, will move nearer and nearer the number you seek.’ From what I’ve been saying, this is, of course, wrong. Venn should have said (and I assume from the rest of your novel that in some ideal reprint you would like her statement correct): ‘If you throw down the stick repeatedly, and if you keep count of the times it falls touching or crossing a line, as well of the total number of times you toss the stick at all, and if you then divide twice the number of tosses by the number of times the stick touches or crosses a line, the successive numbers you express, as you make more and more tosses, will move nearer and nearer the number you seek.’
There is also a more subtle error present in your discussion of the method. Belham later says that with five hundred tosses he is able to get an estimate of π more accurate than 22/7. Moreover, he claims that with another five hundred tosses the estimate will be ‘a good deal more accurate.’ While this level of accuracy is possible, it is not mathematically probable. If we use 2N/Nc to estimate π, then the expected fractional error in the estimate is given by:
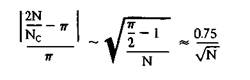
(The symbol ~ means “is equivalent to.”) For N = 500, we can expect on the average the estimate will be accurate to within roughly plus-or-minus 3.4%. In contrast, 22/7 differs from π by only .0040%. For N = 1,000, the expected error is plus-or-minus 2.4%, which is only smaller than the error for N = 500 by a factor of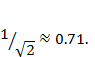 
Because the error decreases only as N gets larger in the expression 
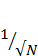that is, because with large numbers the reciprocals of square roots decrease rather slowly as the base number increases), it is hard to obtain very accurate estimates. To achieve an expected accuracy of plus-or-minus 0.0040%, you would need to toss the stick approximately three-and-a-half million times! And even if you had the persistence to toss the stick that often, the accuracy of the estimate would potentially fall short of prediction, unless the apparatus used in the experiment was made with great care:
If the stick is ten centimeters long, the spacing of the lines must be controlled to within four one-hundredths of a millimeter if you want an accuracy of 0.04%. So ‘Venn’ method does not provide a very efficient means for determining π—although it does provide an image that resonates nicely with the rest of your story.
The conclusions above are based on an analysis of the method which I will enclose with this letter.
[Here is the opening of Wentworth’s Analysis of an Experiment for Determining Pi:]
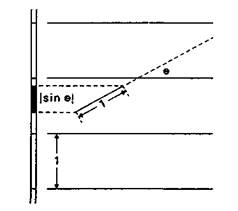
Consider an experiment in which a stylus is tossed onto a sheet of paper ruled with parallel lines spaced one stylus-length apart. The stylus is assumed to land at a random position on the paper and with a random orientation. Once the stylus lands, we observe whether it crosses (or touches) a ruled line, or whether it lies free.
The situation that applies in a single trial is illustrated in the sketch above. The stylus lands so that it is oriented at some angle with respect to the ruled lines. Assume for the moment that θ is known.
Let us project the ruled lines and the image of the stylus onto a line perpendicular to the ruled lines. (See illustration.) The ruled lines become points one stylus-length apart. The stylus is projected to become a length of | sin θ | stylus lengths, where the bars denote absolute value or magnitude.
Given θ , what is the probability that the projection of the stylus covers one of the points associated with the ruled lines? Since the stylus projection has length |sin θ | and the points are separated by a distance 1, it is intuitively true that this probability must be given by:
P(cross| θ) = | sin θ |
Here P(cross| θ) denotes ‘the probability that the stylus crosses a ruled lined, given θ.’
Now we must take into account the fact that in general θ is not known. θ is in fact random. Since all stylus orientations are equally likely, θ may take on any value between zero and 2π radians, and the probability that θ lies between, say, θ0 and θ0 + dθ is given by dθ/27r. Thus the probability that the stylus crosses a line and has an orientation such that θ is between θ0 and θ0 + dθ is given by:
But of course this is not really the probability in which we are interested: we would like to know the probability that the stylus crosses a line independent of any consideration involving θ. To obtain this, we integrate the above probability over all possible values of θ, thus adding up the probability contributions associated with all possible orientations:
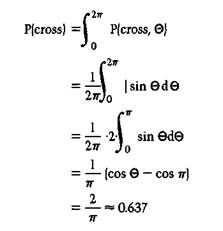
The probability that the stylus crosses a line is 2/π. Since the stylus either crosses a line or lies free—and since all probabilities must add up to one—the probability that the stylus lies free is given by:
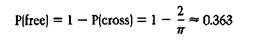
Given the above results, how can the experiment be used to determine π? Well, suppose one tries the experiment N times. On average, the number of times, Nc, that the stylus crosses a ruled line and the number of times, NF, that the stylus lies free will be given respectively by:
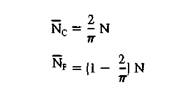
where the overbars denote ‘average’ or ‘expected value.’ If N is large, we expect that N̄c will be close to Nc and N̄F will be close to NF. Given the above formulas for Nc and NF, we see that π may be estimated from the formula:
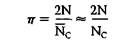
Note that if we take the ratio of Nc/NF we find:
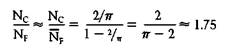
This does not directly provide an estimate of π…
[Wentworth’s analysis goes on to ask, ‘Suppose we use 2N/NC to estimate π. How good an estimate can we expect this to provide? Or, equivalently, how close can we expect Nc to be to (2/π)N? The answer is worked out; and, with the aid of the formula for the mean square deviation from the mean, the answer already expressed in the letter is arrived at. Wentworth’s letter itself goes on:]
I am a great believer in the infallibility of mathematics—but mathematicians are fallible, so I performed an experiment to check my conclusions. I tossed a stick onto a page with ruled lines one stick-length apart 125 times. The stick landed across a line 84 times and between lines 41 times. Thus 2N/Nc is approximately equal to 2.98. This, as an estimate of π, is off by about minus 5%. For 125 tosses, my formula predicts an accuracy on the order of plus-or-minus 6.8%. Thus the experimental results are consistent with the theoretical ones.
End of nitpicking, I do enjoy your work, and I wish you the best of luck with future endeavors.
Sincerely yours,
Robert Wentworth
P.S.—Since writing this letter, I’ve stumbled across a description of the π-determining experiment in a probability text (Papoulis: Probability, Random Variables, and Stochastic Processes, p. 185); the answer for the probability of crossing a ruled line agrees with the result I calculated. Papoulis calls the experiment ‘Buffon’s Needle.’
Also, a friend who is usually right tells me that, my argument about its improbability not withstanding, some historical figure (whose name he didn’t remember) really did use the stick-tossing experiment to determine π to a high degree of accuracy. Very strange. Perhaps you already know all about this…
from:
Samuel R. Delany,
November 7, 1984
Dear Robert Wentworth,
Thanks so much for your letter of 21 September on the mathematics of Venn’s solution to Belham’s problem. It was extremely kind of you to forward me your analysis.
‘Buffon’s Needle,’ hey? I assume that’s the same Buffon who once said: ‘Le style, c’est l’homme même.’—His style, that’s the man himself. Well, Professor Kermit’s protestations to Charles Hoequist aside, I don’t want to fall into the style of those who go on perpetuating misinformation once they have the facts.
A science writer and friend named Monte Davis (co-author of Catastrophe Theory, Davis & Woodcock, Avon Books: New York, 1980) leveled some criticism at the other example of Venn’s ingenuity from Neveryóna’s Chapter 8, i.e., Venn’s machine model for demonstrating fluid-containment replication:
Though in principle (Monte explained one pleasant afternoon when I was signing books down at New York’s Science Fiction Shop) Venn’s demonstration is correct, for the real ‘demonstration machine’ to operate as I described it, water just won’t do for the communicating fluid between the upper and lower basins. Nor will ordinary sand—even very fine sand—suffice as the imprint material in the lower tub. Rather, the upper container would require flooding with some ideally non-turbulent liquid, possibly a very light but very dense polymer oil (if there were such a thing). With most real liquids, however, the entrance into the pipe, the trip down, and the exit from the spigot at the bottom would add so much ‘noise’ to the ‘message’ that, in practical terms, little or none of that ‘message’ would enter the bottom basin intact. Similarly, the imprint medium in the bottom tub would have to be almost weightless. Nor could it mix with the incoming liquid. Rather, it would have to be immediately and ideally displaced. It seems I was led astray by some impressive photographs in Rene Thorn’s Structural Stability and Morphogenesis (i.e., illustration ten following page 167) that were, indeed, photographs of prepared models—not of real experiments. The captions to the pictures, however (printed several pages later), left it very unclear; and to learn that they were, indeed, models, rather than actual experiments, you had to negotiate a particularly daunting stretch of text. And I, I’m afraid, blew it.
In the forth-coming Grafton edition I shall try to make whatever minuscule repairs I can.
But to claim Nevèrÿon is fantasy and try to excuse my blunders on such grounds is a kind of fudging I don’t think I should even flirt with. Thank you, rather, for taking the time to set me straight; and, along with Davis’s conversational comments about the fluid-replication model, I want to lay out these facts before my readers. Ideally, I should like to print some of this correspondence as an appendix, if you agree to it. At any rate, let me acknowledge, and apologize for, my errors. Thanks also for your kind words on my tale.
All best wishes,
Samuel R. Delany