Figure 9-1: A harmonic interval is two notes played simultaneously.
Chapter 9
Intervals: The Distance between Pitches
Understanding the different kinds of intervals
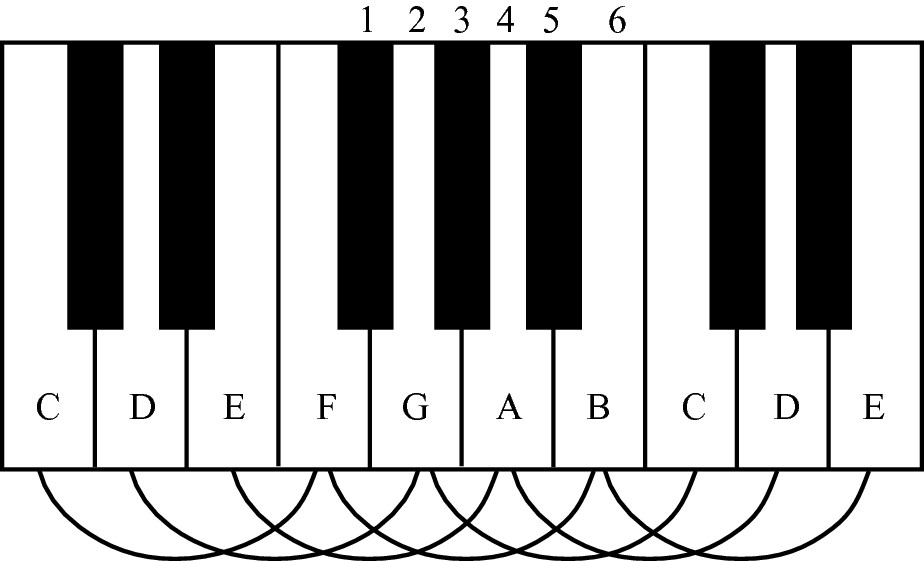
Checking out unisons, octaves, fourths, and fifths
Figuring out seconds, thirds, sixths, and sevenths
Creating your own intervals
Seeing how intervals relate to the major scale
The distance between two musical pitches is called an interval. Even if you’ve never heard the word interval used in relation to music before, if you’ve listened to music, you’ve heard how intervals work with one another. If you’ve ever played music, or even just accidentally set a coffee cup down on a piano keyboard hard enough to make a couple of jangly notes sound out, you’ve worked with intervals. Scales and chords are both built from intervals. Music gets its richness from intervals. This chapter reviews the types of intervals most commonly used in music and discusses how intervals are used in building scales and chords.
Breaking Down Harmonic and Melodic Intervals
The following two types of intervals exist:
A harmonic interval is what you get when you play two notes at the same time, as shown in Figure 9-1.
A melodic interval is what you get when you play two notes separately in time, one after the other, as shown in Figure 9-2.
Figure 9-2: A melodic interval is two notes played one after the other.
The identity of an interval, and this goes for both harmonic and melodic intervals, is determined by two things:
Quantity
Quality
We explain what we mean by each of these in the following sections.
Quantity: Counting lines and spaces
The first step in naming an interval is finding the distance between the notes as they’re written on the staff. The quantity, or number size, of an interval is based on the number of lines and spaces contained by the interval on the music staff. Musicians and composers use different names to indicate the quantity of intervals:
Unison (or prime)
Second
Third
Fourth
Fifth
Sixth
Seventh
Octave
You determine an interval’s quantity by simply adding up the lines and spaces included in the interval. You must count every line and every space between the notes as well as the lines or spaces that the notes are on. Accidentals don’t matter when counting interval quantity.
Take a look at Figure 9-3 for an example of how easy it is to determine an interval’s quantity. If you start on either the top or bottom note and count all the lines and spaces contained in the interval in the figure, including the lines or spaces that contain both notes, you end up with the number five. Therefore, the interval in Figure 9-3 has the quantity, or number size, of five, or a fifth. Because the notes are written together to be played at the same time, it’s a harmonic fifth.
Figure 9-3: The five lines and spaces in this interval’s total quantity indicate this interval is a fifth.
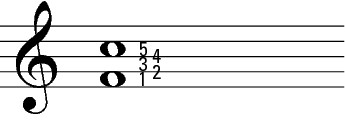
Figure 9-4 shows a melodic second. Note that the sharp accidental (the s) on the F does absolutely nothing to the quantity of the interval. Interval quantity is only a matter of counting the lines and spaces. (You can read about accidentals in Chapter 6.)
Figure 9-4: The fact that the first note is F sharp doesn’t affect the quantity of the interval.
Figure 9-5 shows interval quantities from unison (the two notes are the same) to octave (the two notes are exactly an octave apart) and all the intervals in between. Sharps and flats are thrown in for fun, but remember, they don’t matter when it comes to interval quantity.
Figure 9-5: Melodic intervals in order from left to right: unison, second, third, fourth, fifth, sixth, seventh, and octave.
What if an interval spans more than one octave? In that case, it’s called a compound interval. As with all interval quantities, you just count the lines and spaces for a compound interval. The example shown in Figure 9-6 has the quantity of ten and is therefore called a tenth.
Figure 9-6: A compound interval with a total quantity of ten, which is called a tenth.
Quality: Considering half steps
Interval quality is based on the number of half steps from one note to another. Unlike in interval quantity, accidentals (sharps and flats), which raise or lower a pitch by a half step, do matter in interval quality. (See Chapter 6 for details on accidentals.) Interval quality gives an interval its distinct sound.
Each of the intervals shown in Figure 9-7 have exactly the same quantity, but they sound different because each one has a different quality.
Figure 9-7: All these intervals are fifths, but the various qualities of the fifths make them sound different.
Play Track 61 to hear the differences between the intervals that have the same quantity (fifth) but different qualities.
The terms used to describe quality, and their abbreviations, are as follows:
Major (M): Contains two half steps between notes
Minor (m): Contains a half step less than a major interval, or one half step between notes
Perfect (P): Refers to the harmonic quality of unisons, octaves, fourths, and fifths
Diminished (dim): Contains a half step less than a minor or perfect interval
Augmented (aug): Contains a half step more than a major or perfect interval
Naming intervals
Every interval gets its full name from the combination of both the quantity and the quality of the interval. For example, you may encounter a major third or a perfect fifth. (You can read more about interval quantity and quality in the previous sections.)
Here are the possible combinations that you use when describing intervals:
Perfect (P) can only be used with unisons, fourths, fifths, and octaves.
Major (M) and minor (m) can only be used with seconds, thirds, sixths, and sevenths.
Diminished (dim) can be used with any interval, with the exception of unisons.
Augmented (aug) can be used with any interval.
Looking at Unisons, Octaves, Fourths, and Fifths
Unisons, octaves, fourths, and fifths share the same characteristics in that they all use the terms perfect, augmented, or diminished to identify their quality. (See the earlier section “Quality: Considering half steps” for more information.)
Perfect unisons
A perfect melodic unison is possibly the easiest move you can make on an instrument (except for a rest, of course). You just press a key, pluck, or blow the same note twice. You can play unisons on most stringed instruments because the same note occurs more than once on these instruments, such as on the guitar (the 5th fret on the low E string is the same as the open A string, for example).
In music written for multiple instruments, a perfect harmonic unison occurs when two (or more) people play exactly the same note, in the exact same manner, on two different instruments.
Augmented unisons
To make a perfect unison augmented, you add one half step between the notes. You can alter either of the notes in the pair to increase the distance between the notes by a half step.
The interval from B flat to B is called an augmented unison (or augmented prime) — unison because the note names are the same (both Bs) and augmented because the interval is one half step greater than a perfect unison.
A diminished unison doesn’t exist, because no matter how you change the unisons with accidentals, you’re still adding half steps to the total interval.
Octaves
When you have two notes with an interval quantity of eight lines and spaces, you have an octave. A perfect octave is a lot like a perfect unison in that the same note (on a piano, it would be the same white or black key on the keyboard) is being played. The only difference is that the two notes are separated by 12 half steps, including the starting note, either above or below the starting point.
The perfect melodic octave in Figure 9-8 has 12 half steps between the notes.
Figure 9-8: These two E notes are a perfect octave.
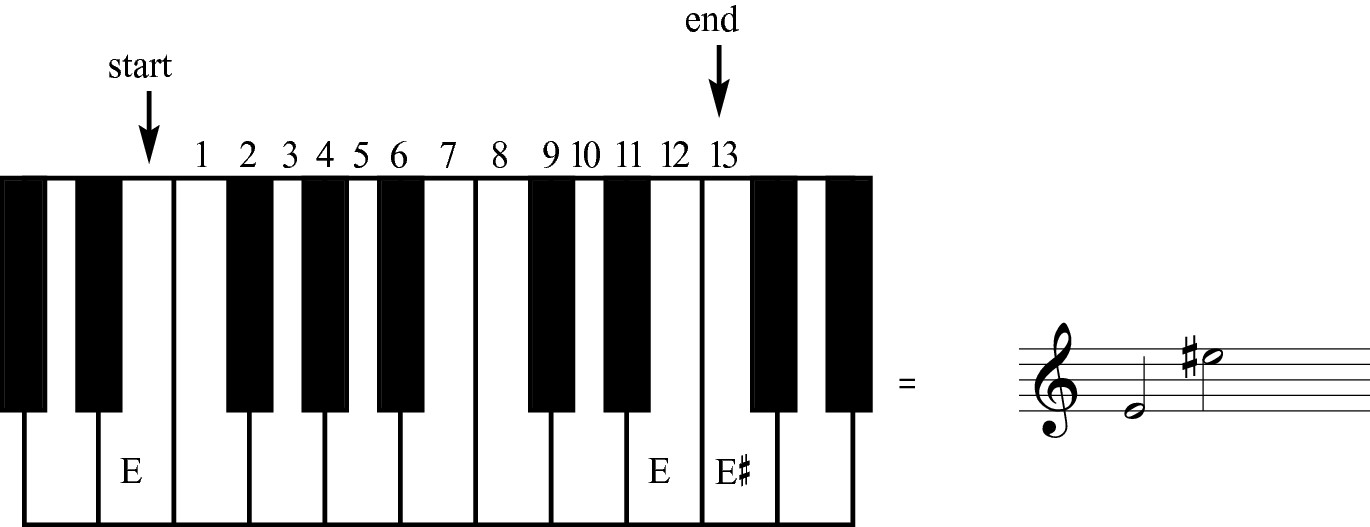
To make a perfect octave augmented, you increase the distance between the notes by one more half step. Figure 9-9 shows an augmented octave from E to E sharp. It was augmented by raising the top note a half step so that 13 half steps come between the first note and the last. You could also make an augmented octave by lowering the bottom E note a half step to E flat.
Figure 9-9: These two notes make an augmented octave.
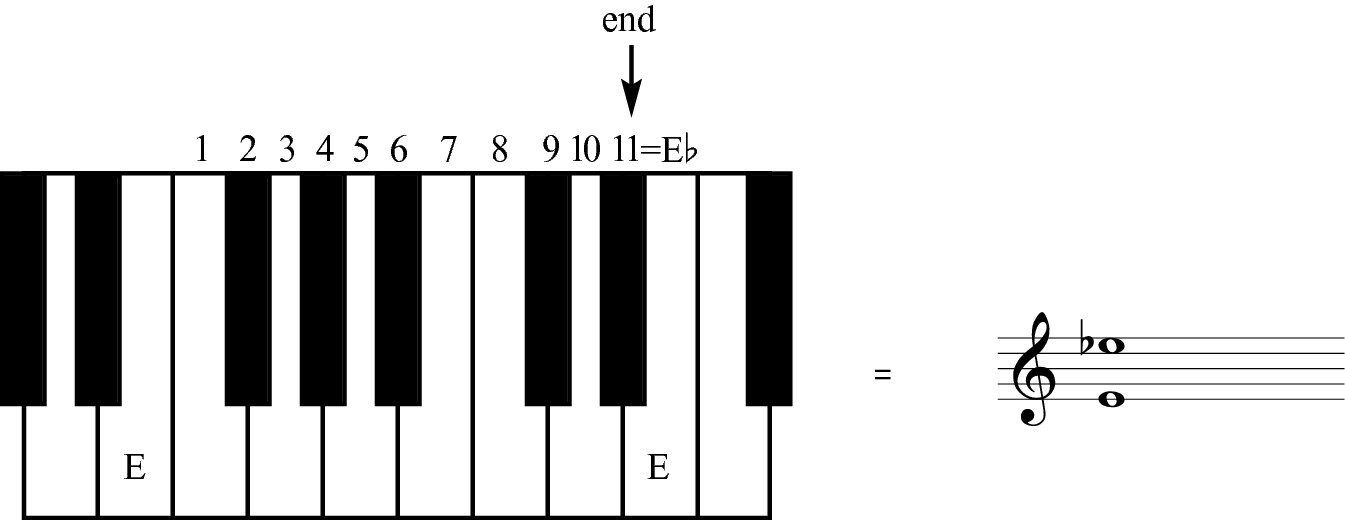
To make the same octave diminished, you decrease the distance between the notes by one half step. For example, Figure 9-10 illustrates lowering the top note a half step so that only 11 half steps come between the first note and the last. You could also raise the bottom note by a half step to make another diminished octave.
Figure 9-10: These two notes make a diminished octave.
Fourths
Fourths are pairs of notes separated by four lines and spaces. All fourths are perfect in quality, containing five half steps between notes — except for the fourth from F natural to B natural, which contains six half steps (making it an augmented fourth). Compare the note pairs in Figure 9-11 on the keyboard to see what we mean.
Figure 9-11: Fourths as seen on the staff with the special (augmented) case of the F natural and the B natural circled.
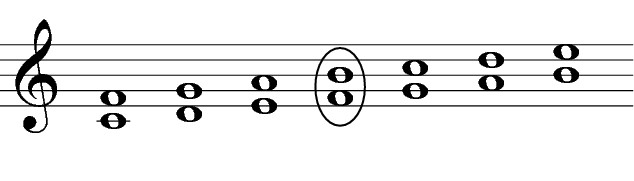
Figure 9-12 shows the connection between each fourth on a keyboard. Note that unlike the rest, the F natural and B natural require six half steps.
Figure 9-12: On the keyboard, every natural fourth is a perfect fourth (except for the interval between F natural and B natural).
Because augmented fourths are a half step larger than perfect fourths, you can create a perfect fourth between the notes F natural and B natural by either raising the bottom note to F sharp or lowering the top note to B flat.
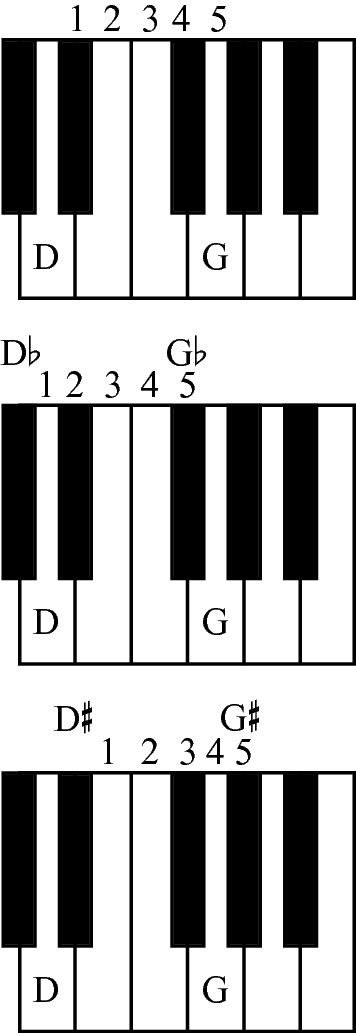
If the natural fourth is perfect, adding the same accidental (either a sharp or a flat) to both notes doesn’t change the interval’s quality. It stays a perfect fourth. The same number of half steps (five) occurs between D natural and G natural that occurs between D sharp and G sharp, or D flat and G flat, as shown in Figures 9-13 and 9-14. If one note changes but the other doesn’t, the quality of the interval does change.
Figure 9-13: Adding accidentals to both notes in a perfect fourth interval doesn’t change it from being a perfect fourth.
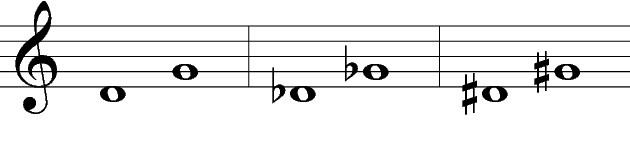
Figure 9-14: You can see on a keyboard the same principle shown in Figure 9-13.
Fifths
Fifths are pairs of notes separated by five lines and spaces (as shown in Figure 9-15). Fifths are pretty easy to recognize in notation, because they’re two notes that are exactly two lines or two spaces apart.
Figure 9-15: Fifths have an interval quantity of five lines and spaces.
All fifths are perfect fifths, meaning that the interval contains seven half steps. However, as you may have guessed, the interval between B to F is a diminished fifth, which turns out to have the same sound as an augmented fourth. Only six half steps occur between those two notes whether you’re going from F natural to B natural or B natural to F natural.
You can create a perfect fifth between F natural and B natural by adding one more half step — either by turning the B natural to a B flat or by raising the F natural to an F sharp. This time, because the notes are flipped around from the order they appeared in the interval of fourths, both changes increase the size of the interval.
Again, just as in a perfect fourth, if a fifth is perfect (every case except F natural and B natural), adding the same accidentals to both notes in the interval doesn’t change its quality. And, as with fourths, if only one of the notes is altered with an accidental, the quality does change.
Recognizing Seconds, Thirds, Sixths, and Sevenths
Seconds, thirds, sixths, and sevenths all share the characteristic of using the terms major, minor, augmented, and diminished to identify their quality. (Check out the earlier section “Quality: Considering half steps” for more information.)
A major interval made smaller by one half step becomes minor, whereas a major interval made larger by one half step becomes augmented. A minor interval made larger by one half step becomes major, and a minor interval made smaller by one half step becomes diminished.
Clear as mud, right? Well, don’t worry. We tell you everything you need to know in the following sections. Also, Table 9-1 summarizes the intervals from unison to octave. Notice in the table that the identity of the interval itself depends on the quantity of the interval number — that is, how many lines and spaces are included in the total interval.
|
Table 9-1 Intervals from Unison to Octave |
|
|
Half Steps between Notes |
Interval Name |
|
0 |
Perfect unison/diminished second |
|
1 |
Augmented unison/minor second |
|
2 |
Major second/diminished third |
|
3 |
Augmented second/minor third |
|
4 |
Major third/diminished fourth |
|
5 |
Perfect fourth/augmented third |
|
6 |
Augmented fourth/diminished fifth |
|
7 |
Perfect fifth/diminished sixth |
|
8 |
Augmented fifth/minor sixth |
|
9 |
Major sixth/diminished seventh |
|
10 |
Augmented sixth/minor seventh |
|
11 |
Major seventh/diminished octave |
|
12 |
Augmented seventh/perfect octave |
|
13 |
Augmented octave |
Seconds
When you have two notes with an interval quantity of two lines and spaces, you have a second, as you can see in Figure 9-16. Seconds are pretty easy to recognize — they’re the two notes perched right next to each other, one on a line and one in a space.
Figure 9-16: These three sets of notes are all seconds.
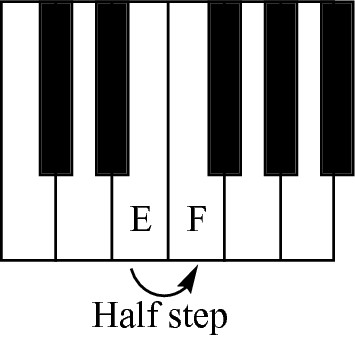
If one half step (one piano key or one guitar fret) exists between seconds, the interval is a minor second (m2). If two half steps (one whole step, or two adjacent piano keys or guitar frets) exist between seconds, the interval is a major second (M2).
For example, the interval between E natural and F natural is a minor second, because one half step occurs between those two notes (see Figure 9-17).
Figure 9-17: The interval between E and F is a minor second, because it only contains one half step.
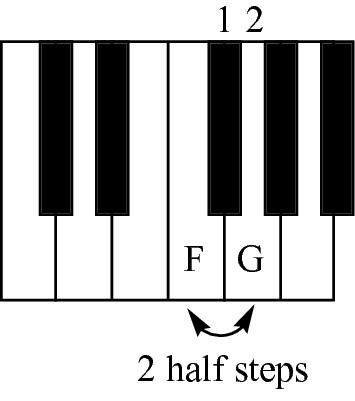
Meanwhile, the interval between F and G is a major second, because two half steps (one whole step) exist between those two notes, as illustrated in Figure 9-18.
Figure 9-18: The interval between F and G is a major second, because it contains two half steps.
A major second is made minor by decreasing its quantity by one half step. You can decrease its quantity either by lowering the top note a half step or raising the bottom note a half step. Both moves reduce the distance between the notes to one half step (one piano key or one guitar fret), as Figure 9-19 shows.
Figure 9-19: Turning a major second into a minor second.
A minor second can be turned into a major second by increasing the interval size by one half step. You can increase the interval size either by raising the top note a half step or by lowering the bottom note a half step. Both moves make the distance between the notes two half steps (two piano keys or three guitar frets).
The only place that half steps occur between white-key seconds is from E natural to F natural and B natural to C natural — the two spots on the keyboard where there are no black keys between the two white keys.
Adding the same accidental to both notes of a natural second doesn’t change its quality. All the seconds shown in Figure 9-20 are major seconds.
Figure 9-20: Major seconds.
All the seconds shown in Figure 9-21 are minor seconds.
Figure 9-21: Minor seconds.
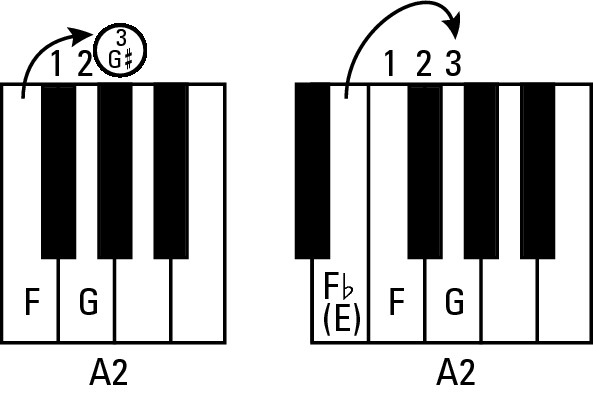
An augmented second is one half step larger than a major second. In other words, three half steps exist between each note. You turn a major second into an augmented second either by raising the top note or lowering the bottom note one half step, as shown in Figures 9-22 and 9-23.
Figure 9-22: Turning a major second interval into an augmented second.
Figure 9-23: Turning a major second interval into an augmented second on the piano: F to G sharp, and F flat to G.
A diminished second is one half step smaller than a minor second — meaning no steps occur between each note. They’re the same note. A diminished second is an enharmonic equivalent of a perfect unison. You’re playing the same two notes, but the notation for the pair is different.
Thirds
Thirds occur when you have an interval that contains three lines and spaces as Figure 9-24 does.
Figure 9-24: Thirds are located on adjacent lines or spaces.
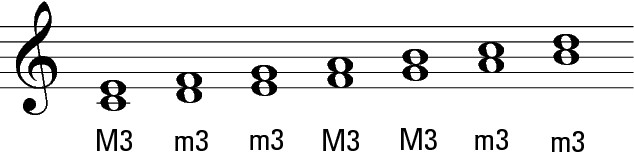
If a third contains four half steps, it’s called a major third (M3). Major thirds occur from C to E, F to A, and G to B. If a third contains three half steps, it’s called a minor third (m3). Minor thirds occur from D to F, E to G, A to C, and B to D.
Figure 9-25 shows major and minor thirds on the musical staff.
Figure 9-25: Major and minor thirds on the staff.
A major third can be turned into a minor third if you decrease its interval size by one half step, making the total three half steps between notes. You can decrease its interval size either by lowering the top note a half step or raising the bottom note a half step (see Figure 9-26).
Figure 9-26: Turning a major third into a minor third.
A minor third can be turned into a major third by adding one more half step to the interval, either by — you guessed it — raising the top note a half step or by lowering the bottom note a half step, as shown in Figure 9-27.
Figure 9-27: Turning a minor third into a major third.
As with seconds, fourths, and fifths, the same accidental added to both notes of a third (both major and minor) doesn’t change its quality; and adding an accidental to just one of the notes of a third does change its quality.
An augmented third is a half step larger than a major third, with five half steps between notes. Starting from a major third, raise the upper note a half step or lower the bottom note a half step. Figure 9-28 shows augmented thirds. An augmented third is also the enharmonic equivalent of a perfect fourth — they’re the same note, but the notation is different.
Figure 9-28: Turning a major third into an augmented third.
A diminished third is a half step smaller than a minor third. Beginning with a minor third, either raise the bottom note a half step or lower the upper note a half step, making for an interval of two half steps (see Figure 9-29).
Figure 9-29: Turning a minor third into a diminished third.
Sixths and sevenths
When you have two notes with an interval quantity of six lines and spaces, as in Figure 9-30, you have a sixth. The notes in a sixth are always separated by two lines and a space or two spaces and a line.
Figure 9-30: Harmonic sixth intervals.
When you have two notes with an interval quantity of seven lines and spaces, as in Figure 9-31, you have a seventh. Sevenths always consist of a pair of notes that are both on lines or spaces. They’re separated by three lines or three spaces.
Figure 9-31: Harmonic seventh intervals.
Building Intervals
The first step in building any interval when creating a piece of music is to create the desired quantity, or number size, above or below a given note. Then you determine the quality. We detail each of these steps in the following sections.
Determining quantity
Determining quantity is easy, especially on paper. For, say, a unison interval, just pick a note. Then, right next to the first note, put another one exactly like it.
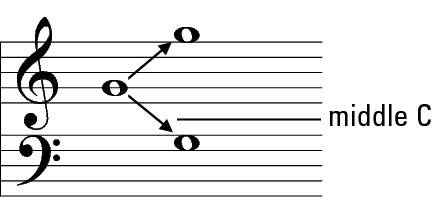
Want to make your interval an octave? Put the second note exactly seven lines and spaces above or below the first, making for a total interval quantity of eight lines and spaces, as shown in Figure 9-32.
Figure 9-32: Octaves of the note G (spanning the two clefs, with middle C indicated).
How about a fourth? Put the second note three spaces and lines above or below the first note, making for a total interval quantity of four lines and spaces. And a fifth? Put the second note four spaces and lines above or below the first note, making for a total interval quantity of five lines and spaces.
Determining quality
The second step to building an interval is to decide what the quality of the interval will be. Say, for example, your starting note is an A flat. And suppose you want your interval to be a perfect fifth above A flat. First, you count out the quantity needed for the fifth interval, meaning you count an additional four spaces above the starting note, making for a total quantity of five lines and spaces, as shown in Figure 9-33.
Figure 9-33: Figuring out the quantity needed to build a perfect fifth above A flat.
Next, you have to alter the second note in order to make it a perfect fifth. Because all fifths are perfect so long as both notes have the same accidental (except for darned B and F), in order to make this pair a perfect fifth, you have to flat the second note so it matches the first, as shown in Figure 9-34.
Figure 9-34: Flatting the second note to match the first makes a perfect fifth.
If you want to make the second note an augmented fifth (aug5, or sometimes A5) below A, you count down an additional four lines and spaces from A to make a total quality of five lines and spaces, and then you write the note, which is D. See Figure 9-35.
Figure 9-35: Building an augmented fifth below A starts with finding the quantity.
Now you alter your added note to make the interval augmented. As you now know, a fifth is an augmented fifth when an additional half step is added to the interval (7 + 1 = 8 half steps), so you would lower the bottom note to a D flat, as shown in Figure 9-36.
Figure 9-36: Adding the accidental makes the interval augmented.
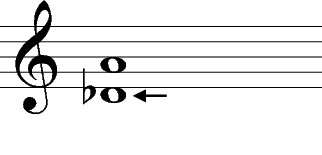
To make the second note a diminished fifth (dim5, or sometimes D5) above A, you count up an additional four lines and spaces, to make a total quality of five lines and spaces, and then write the note, which is E.
Finally, you alter your added note to make the interval diminished. A fifth is a diminished fifth when a half step is removed from the perfect fifth (7 – 1 = 6 half steps), so you would lower the top note to an E flat, as shown in Figure 9-37.
Figure 9-37: Adding the accidental makes the fifth diminished.
Note that a diminished fifth is the same as an augmented fourth — both intervals are made up of six half steps.
Showing Major and Perfect Intervals in the C Major Scale
A scale is really nothing more than a specific succession of intervals, starting from the first note of the scale, or the tonic note. Getting comfortable with intervals and their qualities is the first step to mastering scales and chords. (See Chapters 11 and 12 for much more on major and minor scales.)
Table 9-2, using the C major scale as an example, illustrates the relationship between the first note and every interval used in a major scale.
|
Table 9-2 Intervals in the C Major Scale |
||
|
Note |
Interval from Tonic |
Note Name |
|
First note (tonic) |
Perfect unison |
C |
|
Second note |
Major 2nd (M2) |
D |
|
Third note |
Major 3rd (M3) |
E |
|
Fourth note |
Perfect 4th (P4) |
F |
|
Fifth note |
Perfect 5th (P5) |
G |
|
Sixth note |
Major 6th (M6) |
A |
|
Seventh note |
Major 7th (M7) |
B |
|
Eighth note |
Perfect octave (P8) |
C |
Figure 9-38 shows the intervals from Table 9-2 on the musical scale. These intervals are found in the same order in any major scale. In the major scale, only major and perfect intervals occur above the tonic note. Knowing this can make identifying the qualities of intervals much easier. If the top note of an interval is in the major scale of the bottom note, it must be major (if it’s a second, third, sixth, or seventh) or perfect (if it’s a unison, fourth, fifth, or octave).
Figure 9-38: Simple intervals in the C major scale.
Listen to Track 62 to hear simple intervals in the C major scale.