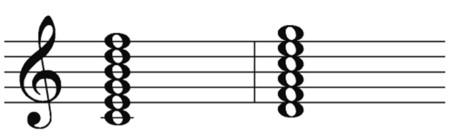
Figure 10-1: Two stacks of thirds, one on the lines and the other in the spaces.
Chapter 10
Chord Building
Getting a grip on major, minor, augmented, and diminished triads
Looking at all the different kinds of seventh chords
Reviewing the triads and sevenths
Inverting and changing voicing for triads and sevenths
A chord is, quite simply, three or more notes played together or, in the case of arpeggiated chords, one after another. By this simple definition, banging a coffee cup or your elbow on top of three or more piano keys at the same time makes a chord — it probably doesn’t sound particularly musical, but it’s still technically a chord.
To the uninitiated and experienced performer alike, chord construction can sometimes seem like magic. There’s something absolutely beautiful and amazing about the way the individual notes in a chord work to enhance one another. Most people don’t appreciate a properly played chord until they hear the way “wrong” notes sound against each other — for example, your coffee cup pushing onto the piano keyboard in a poorly constructed chord.
In most Western music, chords are constructed from consecutive intervals of a third — that is, each note in a chord is a third apart from the one before and/or after it (see Chapter 9 if you need a refresher on your intervals). Figure 10-1 illustrates two stacks of thirds to show you what we mean.
With chords based on intervals of a third, all the notes are either going to be line notes or space notes, resting one on top of another like the examples in Figure 10-1.
Creating Triads with Three Pitches
Triads, which consist of any three pitches from the same scale, are the most common type of chord used in music. Here are the different types of triads you’ll likely work with:
Major
Minor
Augmented
Diminished
In the following sections, we provide information on these triads, but first we introduce what triads are and what they’re made of.
Roots, thirds, and fifths
The term triad refers to chords that contain three different pitches and are built of thirds. The bottom note of a triad is called the root; many beginning music students are taught to think of a triad as being a tree, with the root of a triad being its, well, root. Chords carry the letter name of the root note, as in the root of a C chord, shown in Figure 10-2.
Figure 10-2: The root of a C chord (either C could be the root).
Play Track 63 to hear the root of a C chord.
The second note of a triad is the third (see Chapter 9 for more information about intervals). The third of a chord is referred to as such because it’s a third interval away from the root of the chord. Figure 10-3 shows the root and major third of a C chord.
Figure 10-3: The root and major third of a C major chord.
Play Track 64 to hear the root and major third of a C chord.
The third of a chord is especially important in constructing chords, because it’s the quality of the third that determines whether you’re dealing with a major or minor chord. (We discuss quality more in Chapter 9.)
The last note of a triad is the fifth. This note is referred to as a fifth because it’s a fifth from the root, as shown in Figure 10-4.
Figure 10-4: The root and fifth of a C major chord.
Play Track 65 to hear the root and fifth of a C major chord.
Combine the root, third, and fifth, and you have a triad, such as those shown in Figure 10-5.
Figure 10-5: C major triads.
Play Track 66 to hear a C major triad.
The following sections walk you through building a variety of different triads: major, minor, augmented, and diminished. Table 10-1 has a handy chart to help you keep the formulas straight.
|
Table 10-1 Building Triads |
|
|
Building Triads by Counting Half Steps |
|
|
Major = |
Root position + 4 half steps + 3 half steps (7 half steps above root) |
|
Minor = |
Root position + 3 half steps + 4 half steps (7 half steps above root) |
|
Augmented = |
Root position + 4 half steps + 4 half steps (8 half steps above root) |
|
Diminished = |
Root position + 3 half steps + 3 half steps (6 half steps above root) |
|
Building Triads with Major Scale Degrees |
|
|
Major = |
1, 3, 5 |
|
Minor = |
1, f3, 5 |
|
Augmented = |
1, 3, s5 |
|
Diminished = |
1, f3, f5 |
Major triads
Because they’re made of intervals, triads are affected by interval quality (see Chapter 9 for a refresher on quantity and quality). The quantities of the notes that make up the triad are intervals of root, third, and fifth, but it’s the interval quality of each note that changes the voicing of the triad.
A major triad contains a root, a major third above the root, and a perfect fifth above the root. You can build major triads in two ways. We describe each method in the following sections.
Half-step counting method
You can count out the half steps between notes to build a major triad using this formula:
Root position + 4 half steps + 3 half steps (or 7 half steps above root)
Figure 10-6 shows C major on the piano keyboard. The pattern stays the same no matter the root, but it looks trickier when you move away from C. Notice the pattern of half steps between the root, the third, and the fifth.
Figure 10-6: C major on the keyboard.
First, major third, and fifth method
The second way to construct major triads is to simply take the first, third, and fifth notes from a major scale.
For example, if someone asks you to write down an F major chord, you first write out the key signature for F major, as shown in Figure 10-7. (Review Chapter 8 for more on key signatures.)
Figure 10-7: The key signature for F major.
Then you write your triad on the staff, using F as your root, as seen in Figure 10-8.
Figure 10-8: Add the F major triad.
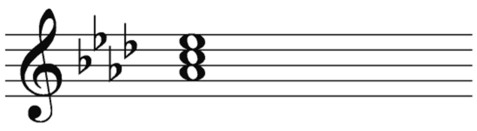
If you were to build an A flat major chord, you would first write down the key signature for A flat major and then build the triad, as shown in Figure 10-9.
Figure 10-9: The A flat major triad.
Minor triads
A minor triad is made up of a root, a minor third above the root, and a perfect fifth above the root. As with major triads, you can build minor triads two different ways, as noted in the following sections.
Half-step counting method
As with major triads, you can count out the half steps between notes to build a minor chord using this formula:
Root position + 3 half steps + 4 half steps (7 half steps above root)
Figure 10-10 shows C minor on the piano keyboard, and Figure 10-11 shows it on the staff. In Figure 10-10, notice the pattern of half steps between the root, the third, and the fifth.
Figure 10-10: C minor on the keyboard.
Figure 10-11: C minor on the staff.
First, minor third, and fifth method
The second way to construct minor triads is to just take the first, the minor or flat third (which means you lower the third degree of the major third one half step), and fifth intervals from a major scale.
For example, for an F minor chord, you write down the key signature for F major and then build the triad, as in Figure 10-12.
Figure 10-12: The F minor triad lowers the third one half step.
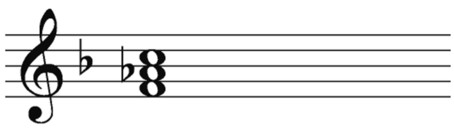
If you were to build an A flat minor chord, you would write the A flat key signature and add the notes, flatting the third, as shown in Figure 10-13.
Figure 10-13: The A flat minor triad lowers the third one half step.
Augmented triads
Augmented triads are major triads that have had the fifth raised a half step, creating a slightly dissonant sound.
An augmented triad is a stack of major thirds with four half steps between each interval.
You can build a C augmented triad (written as Caug) by counting out the half steps between intervals, like this:
Root position + 4 half steps + 4 half steps (8 half steps above root)
C augmented is shown in Figures 10-14 and 10-15.
Figure 10-14: C augmented on the keyboard.
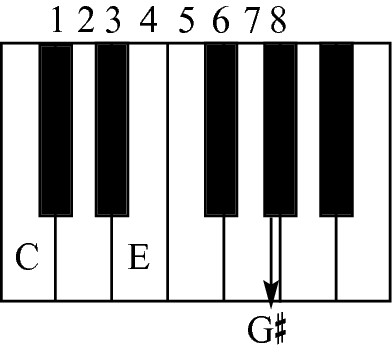
Figure 10-15: C augmented on the staff.
Using the method of starting with the major key signature first and then building the chord, the formula you want to remember for building augmented chords is
Augmented triad = 1 + 3 + sharp 5
So the first major scale degree and third major scale degree stay the same in the chord, but the fifth major scale degree is raised a half step.
It’s important to note here that sharp 5 doesn’t mean that the note will necessarily be a sharp. Instead, it means that the fifth note occurring in the scale degree is raised, or sharped, a half step.
Therefore, if someone asks you to write down an augmented F triad, you first write the key signature for F and then write your triad on the staff, using F as your root and raising the fifth position one half step, as shown in Figure 10-16.
Figure 10-16: The F augmented triad.
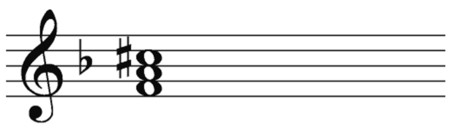
If you were to build an A flat augmented triad, you would go through the same process and come up with a triad that looks like the one in Figure 10-17. Note that the perfect fifth of A flat major is an E flat. Given A flat’s key signature, you have to “natural” the fifth to get to that E natural.
Figure 10-17: The A flat augmented triad.
Diminished triads
Diminished triads are minor triads that have had the fifth lowered a half step.
Diminished triads are stacks of minor thirds with three half steps between each interval.
You can build a C diminished triad (written as Cdim) by counting out the half steps between intervals, like this:
Root position + 3 half steps + 3 half steps (6 half steps above root)
C diminished is shown in Figures 10-18 and 10-19.
Figure 10-18: C diminished on the keyboard.
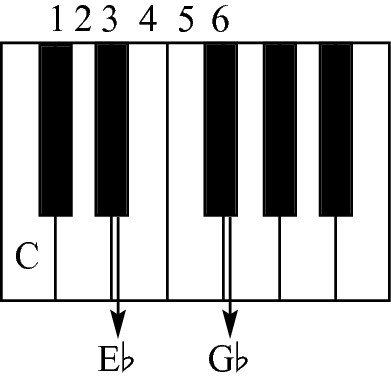
Figure 10-19: C diminished on the staff.
Using the method of starting with the major key signature first and then building the chord, the formula you want to remember for building diminished chords is
Diminished triad = 1 + flat 3 + flat 5
So the first major scale degree stays the same, but the third major scale degree and the fifth major scale degree are both lowered one half step.
It’s important to note here that the terms flat 3 and flat 5 don’t mean these notes will necessarily be flats. These notes are only the third and fifth notes occurring in the scale degree lowered a half step.
Therefore, if someone asks you to write down an F diminished triad, you first write the key signature for F, and then you write your triad on the staff, using F as your root and lowering the third and fifth intervals one half step, as shown in Figure 10-20.
Figure 10-20: The F diminished triad.
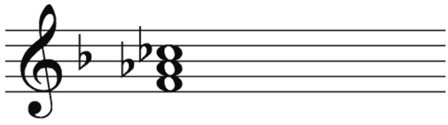
If you were to build an A flat diminished triad, you would go through the same process and come up with a triad that looks like the one in Figure 10-21.
Figure 10-21: The A flat diminished triad.
Note that the perfect fifth of A flat major is an E flat — flatting the fifth makes it a double flat.
Expanding to Seventh Chords
When you add another third above the fifth of a triad, you’ve gone beyond the land of triads. You now have a seventh chord. Seventh chords got their name because the last third interval is a seventh interval above the root.
Several kinds of seventh chords exist. The six most commonly used seventh chords are as follows:
Major sevenths
Minor sevenths
Dominant sevenths
Minor 7 flat 5 chords (also sometimes called half-diminished)
Diminished sevenths
Minor-major sevenths
The easiest way to understand how sevenths are built is to think of each as a triad with a seventh tacked onto it. Looking at sevenths this way, you can see that seventh chords are really just variations on the four triads discussed earlier in this chapter. The names of the chords tell you how to put the seventh together with the triad.
The following sections walk you through building a variety of different sevenths: major, minor, dominant, diminished, and more. Table 10-2 gathers all this info on how to build sevenths.
|
Table 10-2 Building Sevenths |
|
|
Building Sevenths by Counting Half Steps |
|
|
Major = |
Root + 4 half steps + 3 half steps + 4 half steps (11 half steps above root) |
|
Minor = |
Root + 3 half steps + 4 half steps + 3 half steps (10 half steps above root) |
|
Dominant = |
Root + 4 half steps + 3 half steps + 3 half steps (10 half steps above root) |
|
Minor 7 flat 5 = |
Root + 3 half steps + 3 half steps + 4 half steps (10 half steps above root) |
|
Diminished = |
Root + 3 half steps + 3 half steps + 3 half steps (9 half steps above root) |
|
Minor-major = |
Root + 3 half steps + 4 half steps + 4 half steps (11 half steps above root) |
|
Building Sevenths with Major Scale Degrees |
|
|
Major = |
1, 3, 5, 7 |
|
Minor = |
1, f3, 5, f7 |
|
Dominant = |
1, 3, 5, f7 |
|
Minor 7 flat 5 = |
1, f3, f5, f7 |
|
Diminished = |
1, f3, f5, F7 |
|
Minor-major = |
1, f3, 5, 7 |
Major sevenths
A major seventh chord consists of a major triad with a major seventh added above the root. Figure 10-22 shows how to first build a major triad using the C major example from earlier in the chapter.
Figure 10-22: C major triad.
Now add a major seventh to the top of the pile, as is done in Figure 10-23. The result is
C major seventh = C major triad + major seventh interval
Figure 10-23: C major seventh (CM7 or Cmaj7).
B natural is a major seventh from the root of the triad. Notice that it’s also a major third (four half steps) away from the fifth of the triad.
Minor sevenths
A minor seventh chord consists of a minor triad with a minor seventh added above the root. Using the C minor example from earlier in the chapter, you first build a minor triad like the one in Figure 10-24.
Figure 10-24: C minor triad (Cm or Cmi).
Now add a minor seventh to the top of the pile, as is done in Figure 10-25. The result is
C minor seventh = C minor triad + minor seventh
Figure 10-25: C minor seventh (Cm7).
B flat is a minor seventh (ten half steps) from the root of the triad. It’s also a minor third (three half steps) away from the fifth of the triad.
To build a minor seventh using major scale degrees, you pick the first, flatted third, fifth, and flatted seventh degrees from the scale.
Dominant sevenths
A dominant seventh chord, sometimes called a major-minor seventh chord, consists of a major triad with a minor seventh added above the root, as shown in Figure 10-26. The formula for this seventh is
C dominant seventh = C major triad + minor seventh
Figure 10-26: C dominant seventh (C7).
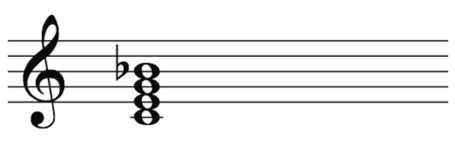
Ten half steps fall between the root and the minor seventh, and three half steps fall between the fifth of the triad and the minor seventh.
The dominant seventh is the only seventh chord that doesn’t truly give away the relationship between the triad and the seventh in its name. You just have to remember it. And don’t confuse major seventh and dominant seventh chords. The major seventh is always written as M7, whereas the dominant seventh is written simply as 7 (occasionally, dom7). For example, G major seventh is written GM7, and the dominant is written G7.
To build a dominant seventh using major scale degrees, you pick the first, third, fifth, and flatted seventh degrees from the scale.
Minor 7 flat 5 chords
A minor 7 flat 5 chord (or half-diminished seventh) is a diminished triad with a minor seventh added above the root. Its name, minor 7 flat 5, tells you everything you need to know about how this chord is supposed to be put together.
Minor 7 refers to the seventh being a minor seventh, or ten half steps, from the root, as shown in Figure 10-27.
Figure 10-27: The root and minor seventh of a C minor 7 flat 5 chord.
Flat 5 refers to the diminished triad, which shares a flatted third with a minor chord but also has a flatted fifth, as shown in Figure 10-28.
Figure 10-28: C diminished triad.
Put the two together, and you have the C minor 7 flat 5 (half-diminished) chord, as shown in Figure 10-29.
Figure 10-29: C minor 7 flat 5 chord.
To build a minor 7 flat 5 (half-diminished) chord using major scale degrees, you pick the first, flatted third, flatted fifth, and flatted seventh degrees from the scale.
Diminished sevenths
The diminished seventh chord is a stack of three consecutive minor thirds. The name is also is a dead giveaway on how the chord is to be built. Just as with the major seventh, which is a major triad with a major seventh, and the minor seventh, which is a minor triad with a minor seventh, a diminished seventh is a diminished triad with a diminished seventh from the root tacked onto it. You can see a diminished seventh in Figure 10-30. The formula for the diminished seventh is as follows:
C diminished seventh = C diminished triad + diminished seventh
Figure 10-30: C diminished seventh (Cdim7).
Note that the seventh in a diminished seventh is double-flatted from the major seventh, so the diminished seventh of Cdim7 is a double-flatted B. Just as with intervals, though, spelling counts — no matter what accidentals appear, a C seventh chord has to have some form of C, E, G, and B.
To build a diminished seventh using major scale degrees, you pick the first, flatted third, flatted fifth, and double-flatted seventh degrees from the scale.
Minor-major sevenths
The name minor-major sevenths isn’t supposed to be confusing. The first part of the name tells you that the first part of the chord, the triad, is a minor chord, and the second part of the name tells you that the second part of the chord, the seventh, is a major seventh above the root.
Therefore, to build a minor-major seventh chord, start with your minor chord, as shown in Figure 10-31.
Figure 10-31: C minor triad.
Then add your major seventh, as in Figure 10-32. The formula is as follows:
C minor-major seventh = C minor + major seventh interval
Figure 10-32: C minor-major seventh (Cm/M7).
To build a minor-major seventh using major scale degrees, you pick the first, flatted third, fifth, and seventh degrees from the scale.
Looking at All the Triads and Sevenths
This section lays out all the types of triads and sevenths we discuss in this chapter in order of appearance and for every key. Figures 10-33 through 10-47 illustrate the triads and sevenths.
A
Play Track 67 to hear the triads and sevenths of A: A major, A minor, A augmented, A diminished, A major seventh, A minor seventh, A dominant seventh, A minor 7 flat 5, A diminished seventh, and A minor-major seventh.
Figure 10-33: A triads and sevenths.
A flat
Play Track 68 to hear the triads and sevenths of A flat: A flat major, A flat minor, A flat augmented, A flat diminished, A flat major seventh, A flat minor seventh, A flat dominant seventh, A flat minor 7 flat 5, A flat diminished seventh, and A flat minor-major seventh.
Figure 10-34: A flat triads and sevenths.
B
Play Track 69 to hear the triads and sevenths of B: B major, B minor, B augmented, B diminished, B major seventh, B minor seventh, B dominant seventh, B minor 7 flat 5, B diminished seventh, and B minor-major seventh.
Figure 10-35: B triads and sevenths.
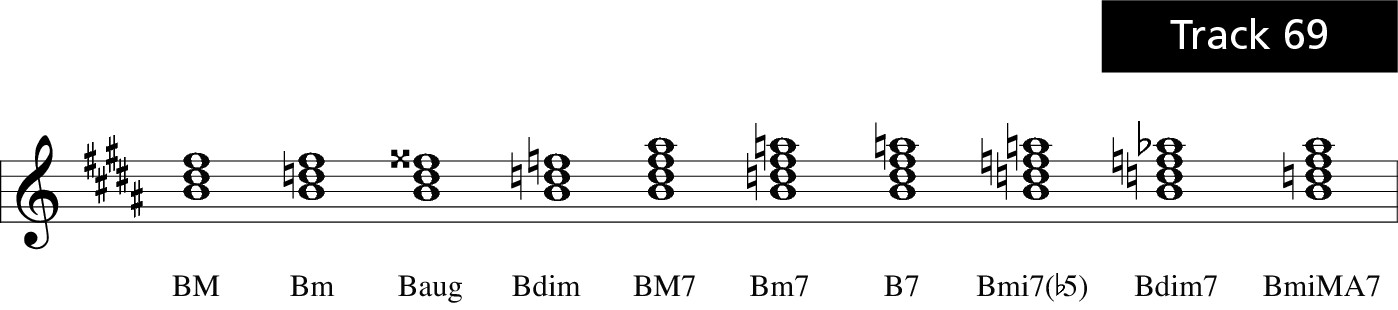
B flat
Play Track 70 to hear the triads and sevenths of B flat: B flat major, B flat minor, B flat augmented, B flat diminished, B flat major seventh, B flat minor seventh, B flat dominant seventh, B flat minor 7 flat 5, B flat diminished seventh, and B flat minor-major seventh.
Figure 10-36: B flat triads and sevenths.
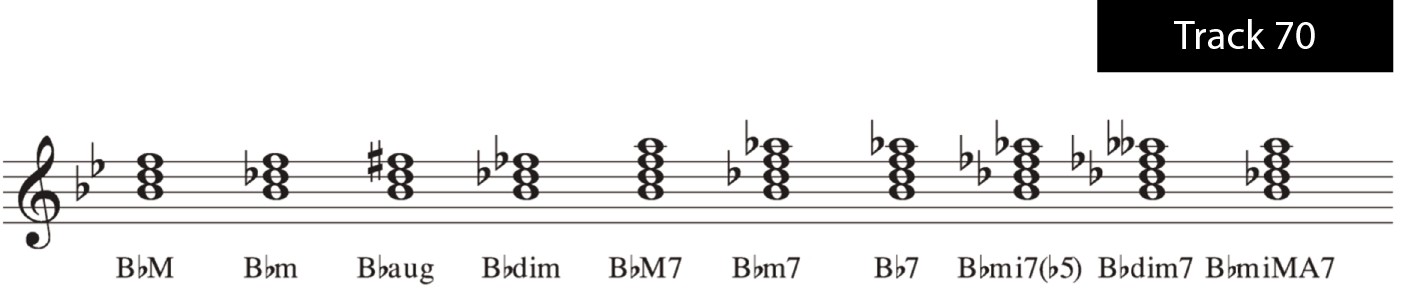
C
Play Track 71 to hear the triads and sevenths of C: C major, C minor, C augmented, C diminished, C major seventh, C minor seventh, C dominant seventh, C minor 7 flat 5, C diminished seventh, and C minor-major seventh.
Figure 10-37: C triads and sevenths.
C flat
Play Track 72 to hear the triads and sevenths of C flat: C flat major, C flat minor, C flat augmented, C flat diminished, C flat major seventh, C flat minor seventh, C flat dominant seventh, C flat minor 7 flat 5, C flat diminished seventh, and C flat minor-major seventh.
Note: C flat is an enharmonic equivalent of B. The chords here sound exactly like the B chords, but in the interest of being complete, we include C flat as well.
Figure 10-38: C flat triads and sevenths.
C sharp
Play Track 73 to hear the triads and sevenths of C sharp: C sharp major, C sharp minor, C sharp augmented, C sharp diminished, C sharp major seventh, C sharp minor seventh, C sharp dominant seventh, C sharp minor 7 flat 5, C sharp diminished seventh, and C sharp minor-major seventh.
Figure 10-39: C sharp triads and sevenths.
D
Play Track 74 to hear the triads and sevenths of D: D major, D minor, D augmented, D diminished, D major seventh, D minor seventh, D dominant seventh, D minor 7 flat 5, D diminished seventh, and D minor-major seventh.
Figure 10-40: D triads and sevenths.
D flat
Play Track 75 to hear the triads and sevenths of D flat: D flat major, D flat minor, D flat augmented, D flat diminished, D flat major seventh, D flat minor seventh, D flat dominant seventh, D flat minor 7 flat 5, D flat diminished seventh, and D flat minor-major seventh.
Figure 10-41: D flat triads and sevenths.
E
Play Track 76 to hear the triads and sevenths of E: E major, E minor, E augmented, E diminished, E major seventh, E minor seventh, E dominant seventh, E minor 7 flat 5, E diminished seventh, and E minor-major seventh.
Figure 10-42: E triads and sevenths.
E flat
Play Track 77 to hear the triads and sevenths of E flat: E flat major, E flat minor, E flat augmented, E flat diminished, E flat major seventh, E flat minor seventh, E flat dominant seventh, E flat minor 7 flat 5, E flat diminished seventh, and E flat minor-major seventh.
Figure 10-43: E flat triads and sevenths.
F
Play Track 78 to hear the triads and sevenths of F: F major, F minor, F augmented, F diminished, F major seventh, F minor seventh, F dominant seventh, F minor 7 flat 5, F diminished seventh, and F minor-major seventh.
Figure 10-44: F triads and sevenths.
F sharp
Play Track 79 to hear the triads and sevenths of F sharp: F sharp major, F sharp minor, F sharp augmented, F sharp diminished, F sharp major seventh, F sharp minor seventh, F sharp dominant seventh, F sharp minor 7 flat 5, F sharp diminished seventh, and F sharp minor-major seventh.
Figure 10-45: F sharp triads and sevenths.
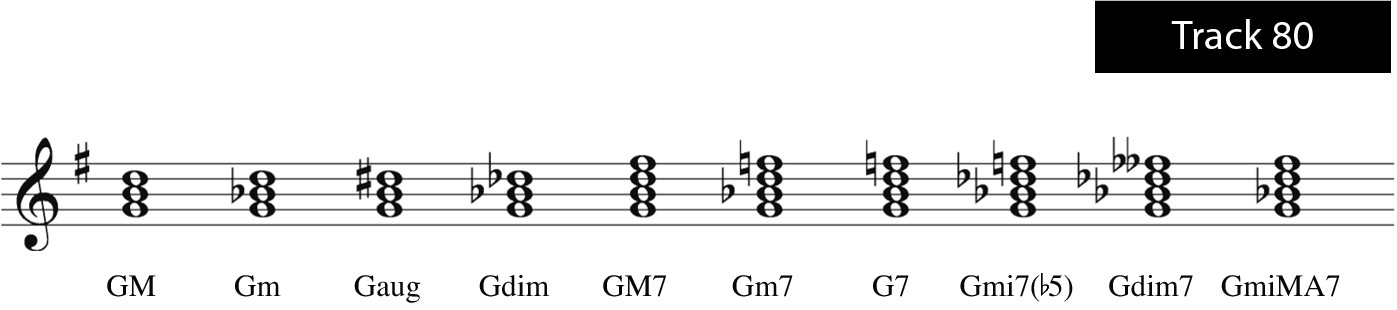
G
Play Track 80 to hear the triads and sevenths of G: G major, G minor, G augmented, G diminished, G major seventh, G minor seventh, G dominant seventh, G minor 7 flat 5, G diminished seventh, and G minor-major seventh.
Figure 10-46: G triads and sevenths.
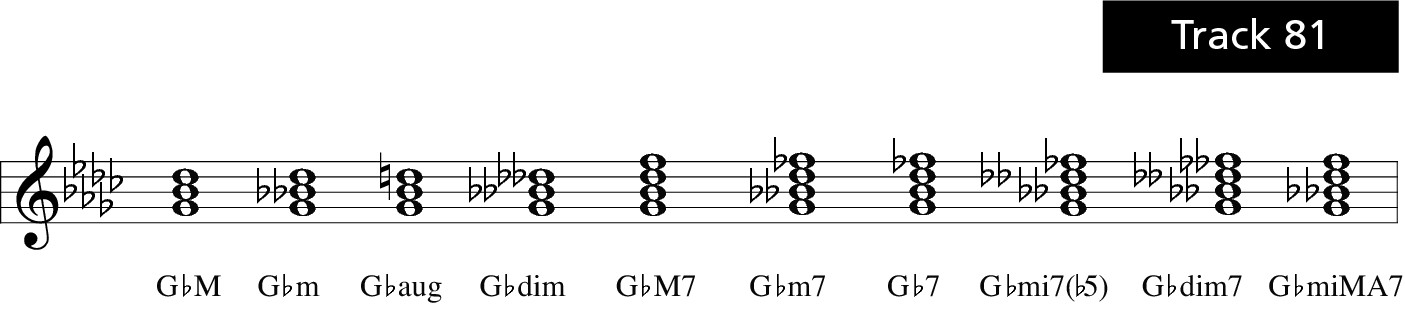
G flat
Play Track 81 to hear the triads and sevenths of G flat: G flat major, G flat minor, G flat augmented, G flat diminished, G flat major seventh, G flat minor seventh, G flat dominant seventh, G flat minor 7 flat 5, G flat diminished seventh, and G flat minor-major seventh.
Figure 10-47: G flat triads and sevenths.
Manipulating Triads through Voicing and Inversion
Here’s a riddle: When is a triad not a perfect little stack of thirds built on top of a root? Answer: when its voicing is open, or when it’s inverted. Voicing, or spacing as it’s referred to in some classical circles, simply refers to the way a chord is arranged.
Taking a look at open and close voicing
Sometimes, the notes of a triad are spread out over two or more octaves, with the different parts rearranged so that, for example, the root may carry the highest-sounding note, or the third, or the fifth can carry the lowest-sounding note. The notes are still the same (C, E, G, for example) — they’re just located an octave or even octaves above or below where you would expect them in a normal triad. When all the notes of a chord are in the same octave, the chord is considered to be in a close voicing.
Figure 10-48 shows a C major chord with close voicing.
Figure 10-48: C major chord with close voicing.
The chord in Figure 10-49, however, is also a C major chord, but with open voicing, meaning that the notes in the chord aren’t all located in the same octave.
Figure 10-49: C major chord with open voicing.
Both chords in Figures 10-48 and 10-49 have the same notes contained in the triad, but in the latter case the third has been raised a full octave from its close position. Both chords are still considered to be in the root position, because the root note, C, is still the lowest note of the triad.
Identifying inverted chords
If the lowest-sounding pitch of a chord is not the root, the chord is considered to be inverted. Here are the possible inversions of a triad:
First inversion: If the third of a chord is the lowest-sounding note, the chord is in first inversion. Figure 10-50 shows the C major chord in first inversion, with close (same octave) and open (different octaves) voicing.
Second inversion: When the fifth of a chord is the lowest-sounding note, the chord is in second inversion. Figure 10-51 shows the C major chord in second inversion.
Third inversion: When the seventh of a chord is the lowest-sounding note, that chord is in third inversion. Figure 10-52 shows the C major 7 chord in third inversion.
Figure 10-50: C major chord in first inversion, close and open voicing.
Figure 10-51: C major chord in second inversion, close and open voicing.
Figure 10-52: C major 7 chord in third inversion, close and open voicing.
So how do you identify inverted chords? Simple: They aren’t arranged in stacks of thirds. To find out which chord it is, you have to rearrange the chord into thirds again. Only one way exists to rearrange a chord into thirds, so you don’t have to guess on the order of the notes. You may need a little patience, though.
Look at, for instance, the three inverted chords shown in Figure 10-53.
Figure 10-53: Inverted chords.
If you try moving the notes up or down octaves (in order to rearrange them so they’re all in stacks of thirds), they end up being an F sharp major triad, a G diminished seventh, and a D major triad (see Figure 10-54).
Figure 10-54: Rearranging the inverted chords into stacks of thirds.
From rearranging the chords, you can tell that the first example was an F sharp major in second inversion, because the fifth was the lowest-sounding note in the chord. The second example was a G diminished seventh, also in second inversion, because the fifth of the chord was at the bottom of the stack. The third example was a D major triad in first inversion, because the third of the chord was the lowest-sounding note.