Newton’s Third Law of Motion
Newton’s third law is sometimes called the law of action and reaction. It states that for every action force, there is an equal and opposite reaction force. For example, let’s say your physics book weighs 6 N. If you set it on a level table, the book exerts 6 N of force on the table. By Newton’s third law, the table must exert 6 N back up on the book. If the table could not return the 6 N of force on the book, the book would sink into the table. We call the force the table exerts on the book the normal force. Normal is another word for perpendicular, because the normal force always acts perpendicularly to the surface that is applying the force (in this case, the table). The force the book exerts on the table and the force the table exerts on the book are called an action-reaction pair.
Newton’s third law is the law of action and reaction.
The normal force FN is the reaction force that a surface exerts on an object and is perpendicular to the surface.
Friction
Friction is a resistive force between two surfaces that are in contact with each other. Friction always opposes the relative motion between the two surfaces. There are two types of friction: static friction and kinetic friction. Static friction is the resistive force between two surfaces that are not moving relative to each other, but that would be moving if there were no friction. A block at rest on an inclined board would be an example of static friction acting between the block and the board. If the block began to slide down the board, the friction between the surfaces would no longer be static, but would be kinetic, or sliding, friction. Sliding friction is typically less than static friction for the same two surfaces in contact.
We can define a ratio that quantifies the roughness between two surfaces in contact with each other. This ratio is the frictional force between the surfaces divided by the normal force acting on the surfaces, and is called the coefficient of friction. The coefficient of friction is represented by the Greek letter µ (mu). Equations for the coefficients of static and kinetic friction are

The frictional force between two surfaces is actually due to the interaction between the electrons in the atoms contained in the two surfaces.
where fs is the static frictional force, fk is the kinetic frictional force, and FN is the normal force*. Sometimes the normal force is represented by N, but as this is easily confused with the newton (N), the unit for force, FN will be used to represent the normal force throughout this book. (Note: There are times when these equations are not quite valid, but we don’t have to worry about those cases for the SAT Subject Test: Physics.)
Example: A 2 kg block rests on a rough horizontal table as shown below. A rope is attached to the block and is pulled with a force of 8 N. As a result, the block accelerates at 2.5 m/s2. What is the coefficient of kinetic friction µk between the block and the table?
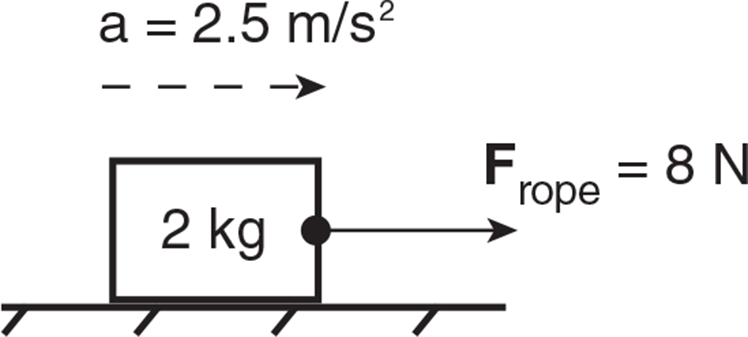
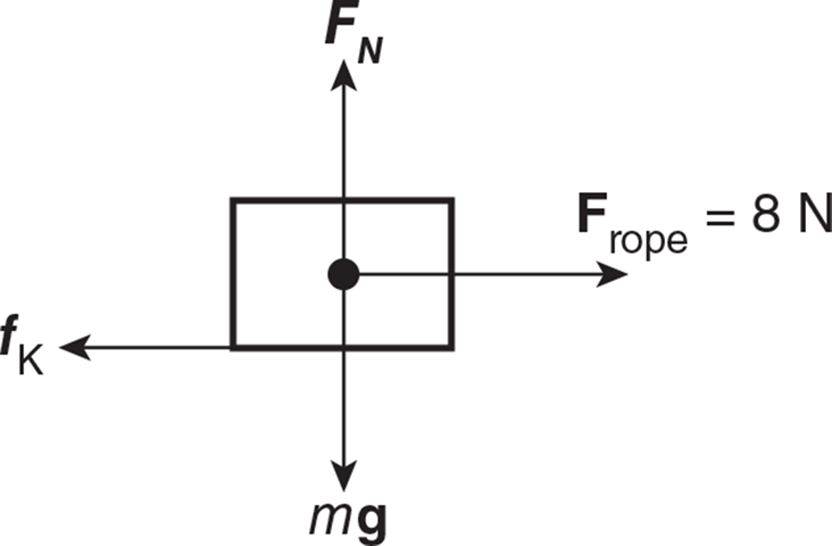
Solution: First, let’s draw all of the forces acting on the block:
Quick Quiz
True or False: The frictional force must equal the weight of the object on which it is acting.
Answer:
False, although it can be proportional to the weight, since sometimes a heavier object creates more friction.
In the vertical direction, the normal force FN must be equal and opposite to the weight W down. Thus:
In the horizontal direction, the net force is the difference between the force Frope the rope exerts on the block and the force of friction fk on the block:
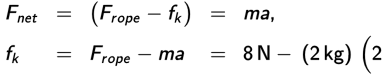
The coefficient of friction is

Notice that the coefficient of friction doesn’t have any units, since it is the ratio of two forces. This is the coefficient of kinetic friction, since the block is moving.
Inclined Plane
If the surface on which the block rests is not horizontal but inclined at an angle, the normal force is not equal and opposite the weight of the block. Let’s look at an example.
Example: A 3 kg block is placed on a rough inclined plane. The coefficient of static friction between the block and the plane is 0.2, and the angle of incline is 30°. Will the block slide down the plane, or remain at rest? (sin 30° = cos 60° = 0.5; cos 30° = sin 60° = 0.87)
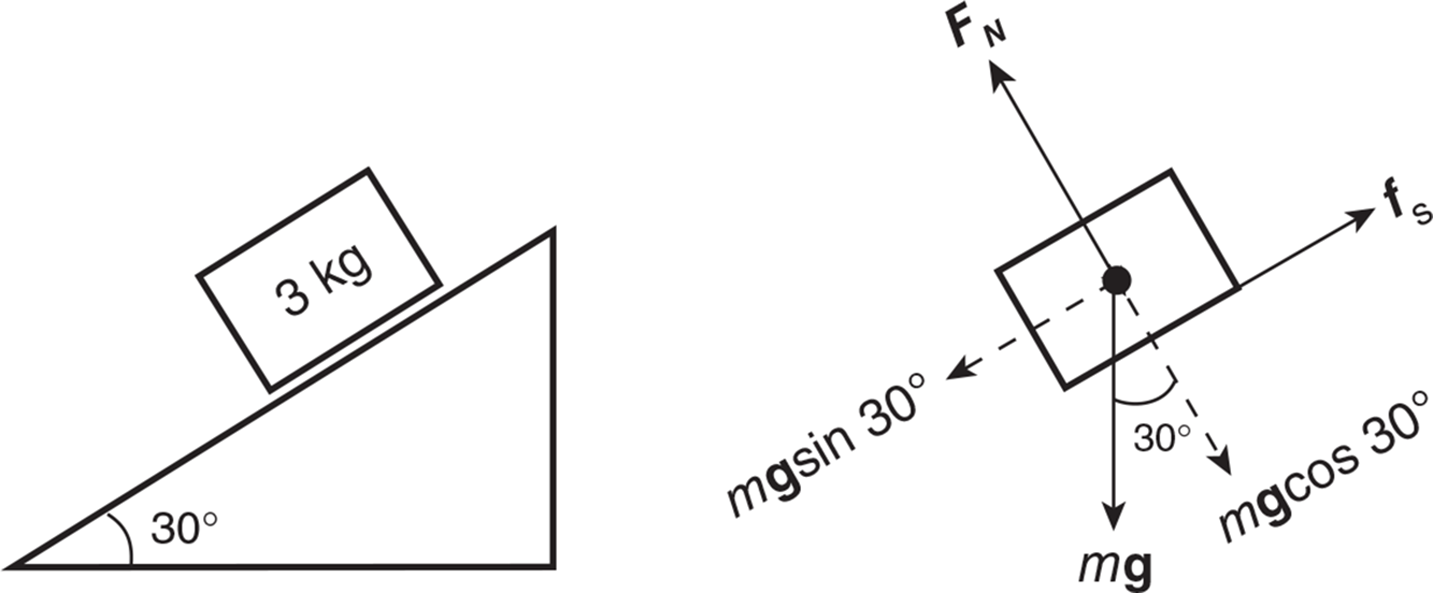
Solution: We see in the free-body force diagram that the frictional force points up the incline to oppose the motion (or impending motion) of the block. What we really want to know is whether or not the component of the weight directed down the incline (mgsin 30°) is greater than the magnitude of the frictional force fs directed up the incline. Calculating each of those forces, we get:
The normal force FN is equal and opposite to the component of the weight that is perpendicular to the ramp, expressed as mg cos 30°. So:

Thus, the force down the incline is greater than the force up the incline, and the block will overcome friction to slide down the incline.