Energy is the ability to do work, and when work is done, there is always a transfer of energy. Energy can take on many forms, such as potential energy, kinetic energy, and heat energy. The unit for energy is the same as the unit for work, the joule. This is because the amount of work done on a system is exactly equal to the change in energy of the system. This is called the work-energy theorem. Let’s look at two examples of the work-energy theorem.
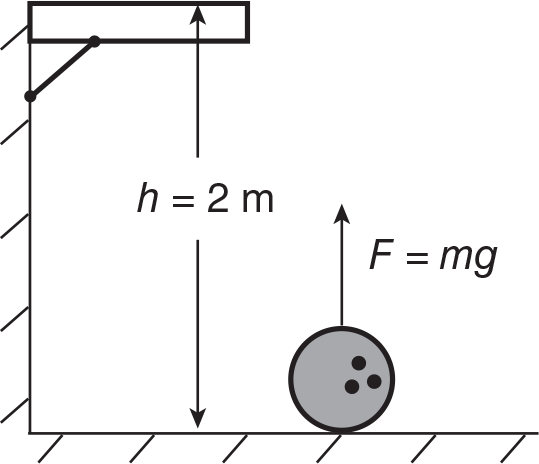
Potential energy is the energy a system has because of its position or configuration. When you stretch a rubber band, you store energy in the rubber band as elastic potential energy. When you lift a mass upward against gravity, you do work on the mass and therefore change its energy. The work you do on the mass gives the mass potential energy relative to the ground. To lift it, you must apply a force equal to the weight mg of the mass through a displacement height h.
The work done in lifting the mass is
which must also equal its potential energy,
Example: A 5 kg bowling ball is lifted straight up to a shelf 2 meters above the floor. What is the work done on the bowling ball, and how much potential energy does the ball have when it is on this shelf?

Solution: The work done in lifting the bowling ball to a height of 2 m is
The potential energy of the ball must also be 100 J relative to the floor, since all of the work done on the ball went into increasing its potential energy.
Kinetic energy is the energy an object has because it is moving. The kinetic energy of a moving object depends on its mass and the square of its velocity:
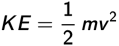
But in order for a mass to gain kinetic energy, work must be done on the mass to push it up to a certain speed or to slow it down. The work-energy theorem states that the change in kinetic energy of an object is exactly equal to the work done on it, assuming there is no change in the object’s potential energy.
Example: A 500 kg car is accelerated from rest by a force of 2,000 N for a displacement of 400 m. What is the speed of the car at the end of 400 m?

Solution: The work done on the car is equal to its change in kinetic energy. The work done is
Thus, the 800,000 J is also equal to the change in kinetic energy of the car:
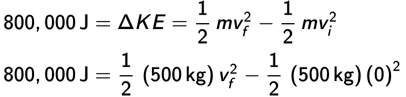
Solving for vf, we get 56.6 m/s.