
Up until this chapter, we’ve been reviewing motion in a straight line. The law of inertia states that if an object is moving, it will continue moving in a straight line at a constant velocity until a net force causes it to speed up, slow down, or change direction. Imagine a ball moving in a straight line in space, but tied to a string as shown in the figure below.

The ball will continue to move in a straight line until it reaches the end of the string, at which time it will be pulled to a central point O and begin moving in a circle. As long as the string is pulled toward this central point, the ball will continue moving in a circle at a constant speed. An object moving in a circle at a constant speed is said to be in uniform circular motion (UCM). Notice that even though the speed is constant, the velocity vector is not constant, since it is always changing direction due to the central force that the string applies to the ball, which we will call the centripetal force Fc. Centripetal means “center-seeking.”
There are three vectors associated with uniform circular motion: velocity (v), centripetal force (Fc), and centripetal acceleration (ac). These vectors are drawn in the diagram below.

Notice that the velocity vector is tangent to the path of the ball and points in the direction the ball would move if the string were to break at that instant. The centripetal force and acceleration are both pointing toward the center. Although the centripetal force does not change the speed of the ball, it is always pulling the ball away from its inertial straight-line path and toward the center of the circle. Thus, the centripetal force accelerates the ball toward the center of the circle, constantly changing its direction.
The time it takes for the ball to complete one revolution is called the period (T). Since period is a time, we will measure it in seconds, minutes, hours, or even years. On the other hand, frequency (f) is the number of revolutions the ball makes per unit time. Units for frequency would include:

Units for frequency can be any time unit divided into revolutions or cycles. Another name for rev/s is hertz. We can relate all of these quantities in the equations that follow.
The constant speed of any object can be found by
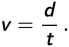
For an object moving in a circle and completing one revolution, the speed of the object can be found by
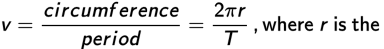
and the centripetal acceleration is

Newton’s second law states that the net force and acceleration must be in the same direction and are related by the following equation:
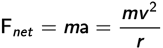
Some other examples of centripetal force are the gravitational force keeping a satellite in orbit, and friction between a car’s tires and the road that causes the car to turn in a circle.
Example:
A 100 kg racecar moves around a flat circular track of radius 50 m with a constant speed. The car makes one revolution around the track every 10 seconds. Find

Solution:

