The Dynamics of Harmonic Motion

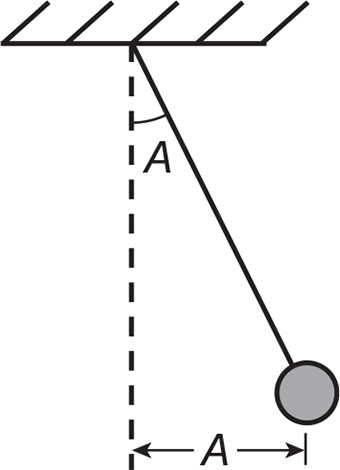
As an object vibrates, it has both a period and a frequency. Recall that the period of vibration is the time it takes for one complete cycle of motion (i.e., the time it takes for the object to return to its original position). For a pendulum, this would be the time for one complete swing, forward and back. The frequency is the number of cycles per unit time, such as cycles per second, or hertz. The period and frequency of a pendulum depend only on the length of the pendulum and the acceleration due to gravity. The lowest point in the swing of a pendulum is called the equilibrium position, and the maximum displacement from equilibrium is called the amplitude. The amplitude can be measured by the maximum angle or by the linear horizontal distance from equilibrium, as shown below.

Since the pendulum vibrates about the equilibrium position, there must be a force that is trying to restore it back toward the center of the swing. This force is called the restoring force, and it is greatest at the amplitude and zero as the pendulum passes through the equilibrium position. Newton’s second law tells us that if there is a net force, there must be an acceleration, and if the force is maximum at the amplitude, the acceleration must be maximum at the amplitude as well. The velocity, however, is zero at the amplitude and maximum as it passes through the equilibrium position. It might be helpful to think of the swing of a pendulum in terms of energy. At maximum amplitude, the pendulum mass has maximum potential energy and no kinetic energy. As it passes through the equilibrium position, all of the potential energy has been converted to kinetic energy.

We can apply these same concepts to a mass vibrating at the end of a spring. On the following figure, we’ve labeled the equilibrium position, the amplitude, maximum force and acceleration, and maximum velocity.

The period and frequency of a mass vibrating on a spring depend on the stiffness of the spring. For a stiffer spring, it takes more force to stretch the spring to a particular length. The amount of force needed per unit length is called the spring constant (k), measured in newtons per meter. The relationship between force, stretched length, and k for an ideal (or linear) spring is called Hooke’s law:

F_spring = kx,

where x is the stretched length of the spring. For an ideal spring, the stretch is proportional to the force. If we pull with twice the force, the spring will stretch twice as far.

A linear spring follows Hooke’s law: The force is proportional to the distance the spring is stretched.

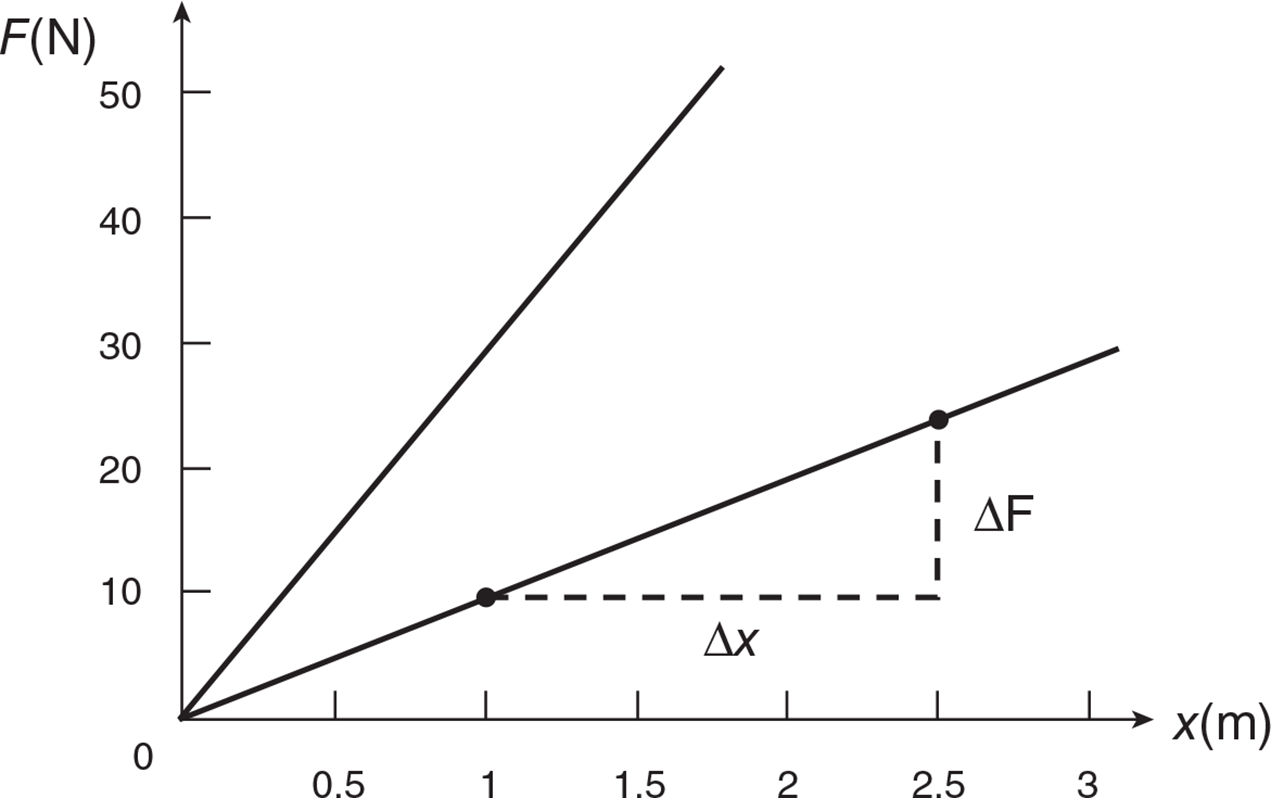
Example: The graph below represents the force F vs. stretched length x for two springs.

• 1. Which is the stiffer spring? Explain.
  2. What is the spring constant for Spring 2?

Solution:

• 1. Spring 1 is the stiffer spring, since it takes more force to stretch it the same length as Spring 2.
  2. We can find the spring constant k for Spring 2 by taking the ratio of the force to the stretch for a particular interval. In other words, we can find the slope of the F vs. x graph for Spring 2.

Quick Quiz

Which of the following occur at the same time for a swinging pendulum?

maximum force, maximum velocity, maximum acceleration, amplitude, equilibrium position

Answer:

The maximum force and acceleration occur when the pendulum is at its amplitude, and the maximum velocity occurs at the equilibrium position.