The standard gates we have worked with so far that rotate around the z axis are the Z, S, S†, T and T† gates, which rotate π, π/2, -π/2, π/4, -π/4 or 180°, 90°, -90°, 45°, and -45° respectively. To implement Rk in IBM QX, as in Python, we will need a way to rotate around the z axis, about the x-y plane, by the number of degrees of our choice, not just a selection of π, π/2, -π/2, π/4, -π/4. To do this, we will use one of the advanced IBM QX gates. Via the quantum composer, click Advanced to see the gates:
Then look at the description of the U1 gate:

In OpenQASM, this gate can be created by using the U gate with parameters 0,0,lambda, where lambda will correspond to the number of radians to rotate by (you can convert from degrees to radians by multiplying by π/180):

You can use the U1 gate in the quantum composer by dragging it to the score, and the user interface will bring up a dialog to select the number of radians that the gate should perform the rotation about the z axis (in the x-y plane) for:
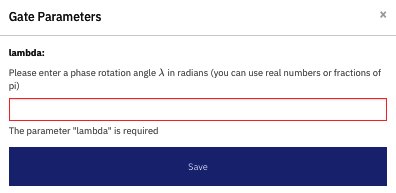
In the end, we will want not only the U1 gate but the controlled U1 gate, CU1, which will perform the role of the controlled Rk gate. This is not available directly in the IBM QX GUI, although with some mathematics we could figure out the equivalent of the CU1 gate in terms of U1 and CNOT gates. Specifically, CU1(λ, control, target) is equivalent to the following:
u1(lambda/2) control;
cx control,target;
u1(-lambda/2) target;
cx control,target;
u1(lambda/2) target;
Here, lambda is in radians. Luckily the CU1 gate is available directly from Qiskit, so that makes things easy: it can simply be called with cu1(lambda,control,target). To find the value of lambda to plug in for a given k, we need to plug in the value for k into the λ = 2π/2k equation.