Specific sets of classic gates, for example the the NOT and AND gates, can be used to construct all other classic logic gates and thus form a set of universal classic gates. Other such sets exist; in fact, the NAND, negative and, gate alone is a universal classic gate. In quantum computation, to obtain a universal gate set we will need a multi-qubit gate, which is applied on 2-qubits of an n-qubit register. The CNOT gate is one such gate. CNOT is the 2-qubit controlled not gate. Its first input is known as the control qubit, the second as the target qubit, and the state of the target qubit is flipped on output if and only if the control qubit is |1>. The application of CNOT can under many scenarios generate entanglement. CNOT combined with single qubit gates can approximate, arbitrarily well, any (unitary) operation on a quantum computer. Quantum gates can be combined to form quantum circuits, the analog to classic circuits composed of logic gates connected by wires. The full set of gates that the IBM QX supports forms a (non-minimal) universal quantum gate set, such that we can combine the gates in a quantum circuit to create any multi-qubit logic gate we desire.
The H gate is also known as a Hadamard gate and is defined as follows:

The X, Y, and Z gates are also known as Pauli gates and are defined as follows:

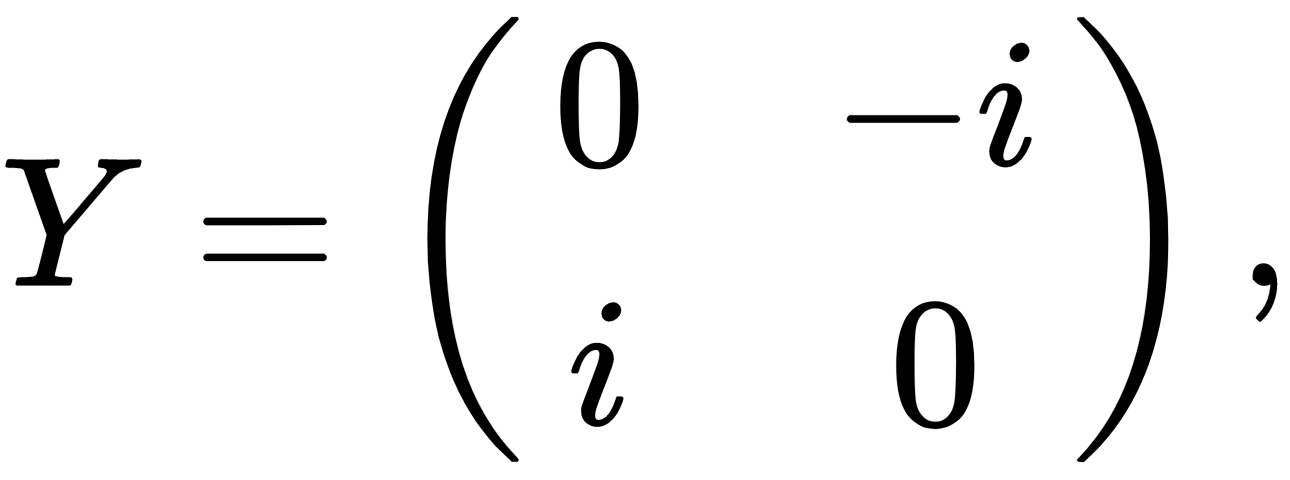
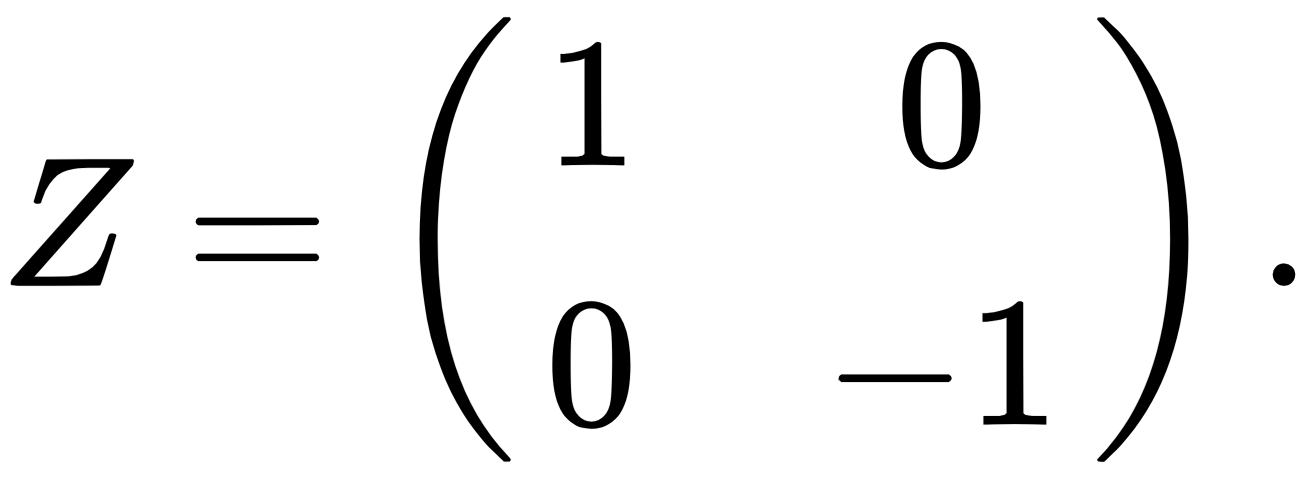
The I gate is also known as an Identity gate and is defined as follows:

The S gate is also known as a Phase gate and is defined as follows:

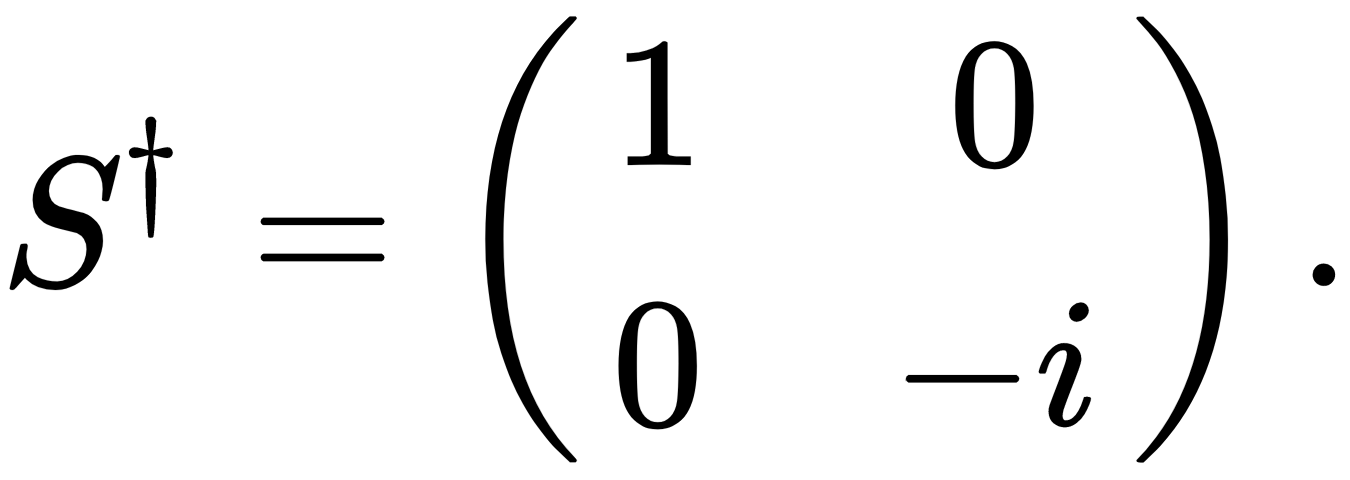
The T gate is also known as a π/8 gate and is defined as follows:
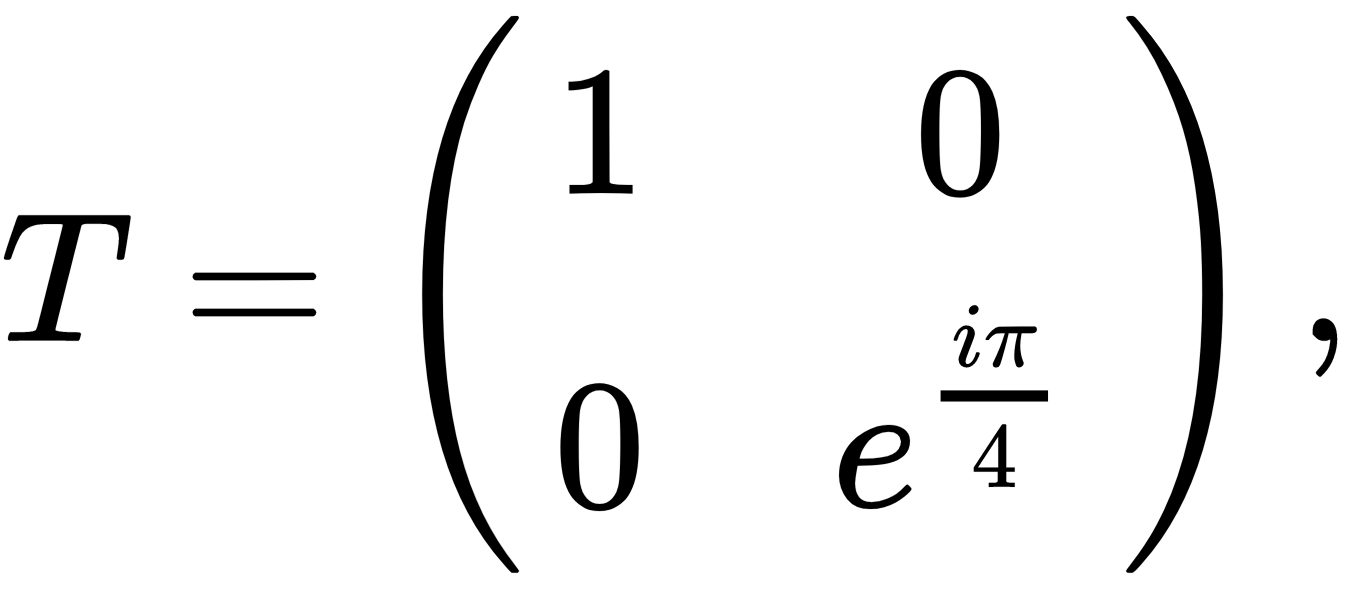
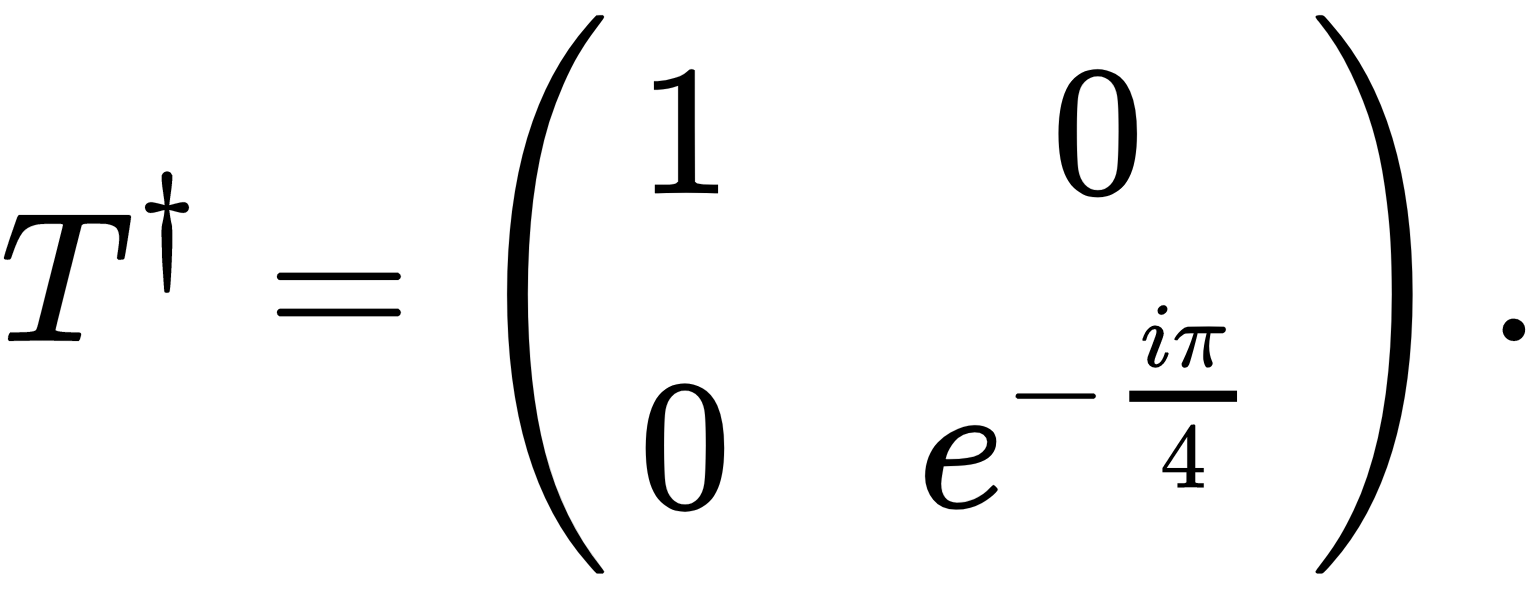
The CNOT gate is also known as a quantum NOT gate and is defined as follows:
