CNOT gate

The CNOT gate stands for the controlled-not gate and always operates on two qubits at once. This gate provides the quantum analogue of the classic XOR gate. The first qubit acts as a control qubit, and never changes as a result of the gate's operation. If this first qubit is |"1">, then a NOT operation is applied to the second qubit. If this first qubit is |"0">, then nothing is done to the second qubit.

This is easy enough to illustrate in a table for states |"00">, |"01">, |"10">, and |"11">:

Starting state	CNOT operating on stating state
|"00">	|"00">
|"01">	|"01">
|"10">	|"11">
|"11">	|"10">

 

The second qubit depends upon the first qubit, so if the first qubit's state changes before input to CNOT, the second qubit will shift. Since this gate is dealing with two qubits, it is not possible to visualize it generally on the Bloch sphere. We will need to make do with words.

If our control qubit is a starting state that is in a superposition between |"0"> and |"1">, things get more difficult to envision in a chart, but we can still think of them in words/algebra or in code. We'll start out in words/algebra and then see how this plays out in code.

First, let's have our control qubit in a state that is halfway between zero and one, the |"+"> qubit. Recall that 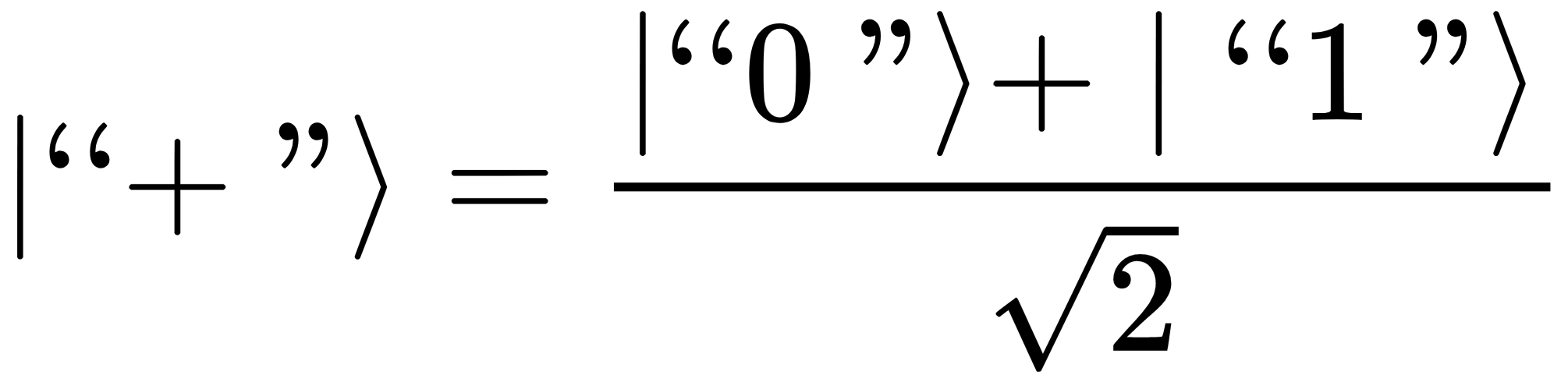 and measuring a |"+"> qubit will result in |"0"> approximately 50% of the time and |"1"> approximately 50% of the time.

We can also create the |"+"> state from |"0"> by operating the Hadamard gate on |"0"> as |"+">. Programming a physical quantum computer often requires starting with qubits in the |"0"> state, so keeping in mind how to apply gates |"0"> to reach other desired starting states is an important skill in quantum programming. It's part of the reason we've focused so much on visualizing the process of obtaining one qubit from another with a variety of gates.

We'll take our second qubit to be the |"0"> state. So we can write our two-qubit state, we start out with (naming it "starting") as:

The |"starting"> state isn't entangled, as we can separate it out into two qubits, the first qubit being |"+"> and the second qubit being |"0">. For the next step, we'll use the fact that 

to rewrite the |"starting"> state as:

I've just chosen to write them together so that, in the next step, when we apply the CNOT gate, it is easier to see what happens.

Now, let's apply the CNOT gate to |"starting"> to get a final state called "final":

So, our final state is this:

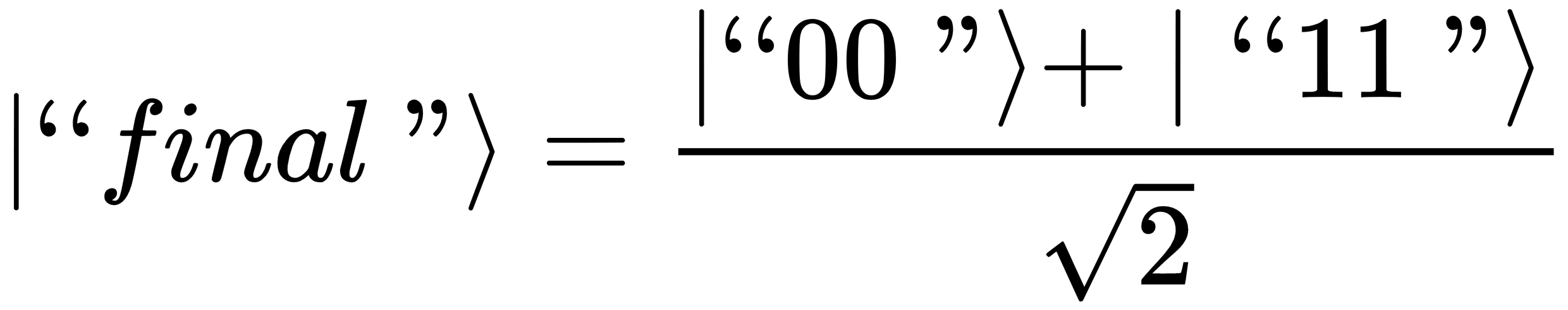
We saw in the last chapter, under the Separable states section, that this state is a non-separable state, so we can no longer talk about the two qubits apart from each other. We saw in the last chapter, under the Entanglement section, that a state that is non-separable is an entangled state. So, we've generated an entangled state from two non-entangled qubits using the CNOT gate. If we measure this entangled state, as we saw in the last chapter, we will get |"00"> approximately 50% of the time and |"11"> approximately 50% of the time.