In quantum mechanics and quantum computing, bra-ket notation is often used to denote a quantum state. For example the following are kets:
 and
and  ,
,
Whereas the following are bras:
 and
and 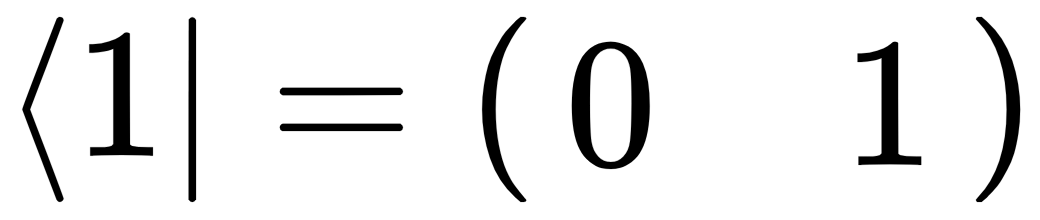 .
.
A ket is simply a matrix in a single column format; whereas a bra is a matrix in a single row format. For the same symbol within a bra or a ket, one is the conjugate transpose of the other. So, <0|* = |0> and |0>* = <0|, and <1|* = |1> and |1>* = <1|. Since the bra and the ket are different shapes (the bra is a 1 by n matrix, whereas the ket is an n by 1 matrix), in general, just because you can multiply a third matrix by one does not mean you can multiply it by the other.