It turns out that any computation you do in a quantum computer can be undone prior to measurement, to get back to exactly what you started with, without knowing what the inputs were. Quantum computing is reversible, which is remarkable because some of the logical operations we might perform in a classical computer can't be reversed.
Consider the classical AND function, which is as follows:
|
Bit 1 |
Bit 2 |
AND(Bit1Bit2) |
|
0 |
0 |
AND(00) = 0 |
|
0 |
1 |
AND(01) = 0 |
|
1 |
0 |
AND(10) = 0 |
|
1 |
1 |
AND(11) = 1 |
If this computation were reversible, we could find an UNDO_AND gate that could get us back to where we started, with two bits, from the output bit alone. If we had a function like that, then UNDO_AND(AND(00)) would equal to 00, UNDO_AND(AND(01)) would equal 01, UNDO_AND(AND(10)) would equal 10, and UNDO_AND(AND(11)) would equal 11. Therefore, UNDO_AND(AND(11)) would work because we know the only combination of inputs that produces 1 is 11. But for the other arguments of AND, we'd have no idea how to make the function UNDO_AND because AND(00), AND(01), and AND(11) all produce the same thing—0. So, how is the function UNDO_AND going to decide which of 00, 01, or 11 to return? The answer is we simply can't make an UNDO_AND function. The only way to undo it would be to memorize the inputs and store them elsewhere. The classical AND gate is not reversible; the information about the inputs is not discernible from the output.
But in quantum computing, every gate is reversible. Depending on the gate, the method of reversing the gate is different. The following table illustrates each gate and how to reverse it:
|
Gate |
Reverse |
|
I |
I |
|
X |
X |
|
Y |
Y |
|
Z |
Z |
|
H |
H |
|
S |
S† |
|
S† |
S |
|
T |
T† |
|
T† |
T |
|
CNOT |
CNOT |
Here we can note that for most gates we have seen so far, the method to undo or reverse the gate is simply to apply the same gate again. The exceptions being, that for the S and T gates, the undo is the corresponding dagger gate S† and T†, undo is the corresponding gate without the dagger. These methods can be combined to reverse any circuit. When written in a circuit diagram it often then looks as if the reverse circuit is a mirror image of the original. When written in words/algebra it is the same, for example, for a single qubit gate XYZS†T†HHTSZYX |"0"> = |"0"> and XYZS†T†HHTSZYX |"1"> = |"1">. The mirror starts right between the H gates in this example, and it is an exact mirror except for the cases of S and T, which switch to their dagger variants.
Here is an example of using every one of the gates we have used so far in a reversible circuit over five qubits:
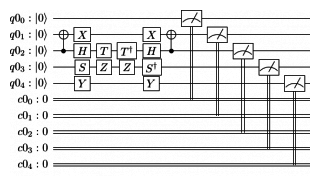
In this example, all the qubits start off at |"0">, so they all end up measuring |"0"> and placing 00000 in the classical register, but the circuit would work for any combination of inputs. |"11111"> would place 11111 in the classical register, |"10101"> would place 10101, and so on. We always get out exactly what we put in because we have followed the prescription for undoing the circuit. This prescription will work for any circuit, no matter how complicated.