We can represent a periodic (that is, repeating) oscillation that is smooth (that is, it has no breaks) by a sine function.
Any sine wave can be written as follows:
f is the number of oscillations per one 
(for the rest of this chapter, let's consider time in units of seconds, so x = 1 corresponds to one second), A is the amplitude or height of the wave, and Φ is the phase, indicating where in the cycle the wave is, in degrees (°). A full cycle is 360°.
We can plot this with the following code:
import numpy as np
import matplotlib.pyplot as plot
def plot_wave(A,f,phi,name=''):
plot.clf()
x = np.arange(0, 1, 0.01);
y = A*np.sin(2*np.pi*f*x + np.pi/180*phi)
plot.plot(x,y)
plot.xlabel('x')
plot.ylabel('y')
plot.title(name)
plot.grid(True, which='both')
plot.axhline(y=0, color='k')
plot.show()
We can plot a wave with an amplitude of 1, a frequency of 1, and a phase of 0, with the following line of code:
plot_wave(1,1,0,'sine wave, A=1, f=1, omega=0')
We can create a similar wave that is a quarter of a cycle out of phase with our original sine wave, or Φ = 360° / 4 = 90°. We can create the wave with the same code, so long as we input these parameters:
plot_wave(1,1,90,'cosine wave, A=1, f=1, omega=0')
Alternatively, there is a shorthand for this type of wave, cos, called the cosine wave. Displayed next to each other, we have the sine wave in green and the cosine wave in blue:
If we add these two waves, the sine and the cosine, together, we'd get the following:
Now, imagine that instead we have a wave with the same amplitude as the original sine wave, only 180° out of phase. Displayed next to each other, with the original sine in green and the 180° out-of-phase version in blue, we have the following:
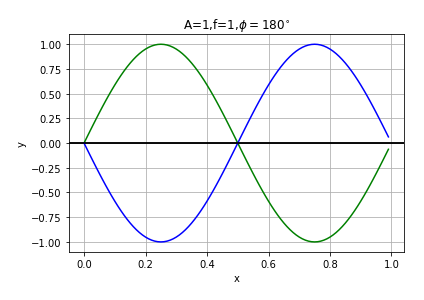
Every time the original wave has a positive value, this wave has the exact same value, only negative. So they completely cancel each other out. If we added the two, we would just get a line at zero, so we say that these two waves destructively interfere:
