IN THE DAYS before Copernicus discovered that the earth revolves around the sun, the common belief was that the sun, along with the rest of the universe, revolved around the earth. The earth was the fixed center of everything. At a still earlier time in India, this geocentric position was given to people. That is, each person, psychologically speaking, was recognized as being the center of the universe. Although this sounds like an egotistical point of view, it was not since every person was recognized as a divine manifestation.
A beautiful Hindu painting shows Lord Krishna dancing in the moonlight on the bank of the Yamuna. He moves in the center of a circle of fair Vraja women. They are all in love with Krishna and they are dancing with him. Krishna is dancing with all of the souls of the world—man is dancing with himself. To dance with god, the creator of all things, is to dance with ourselves. This is a recurrent theme of eastern literature.
This is also the direction toward which the new physics, quantum mechanics and relativity, seems to point. From the revolutionary concepts of relativity and the logic-defying paradoxes of quantum mechanics an ancient paradigm is emerging. In vague form, we begin to glimpse a conceptual framework in which each of us shares a paternity in the creation of physical reality. Our old self-image as impotent bystander, one who sees but does not affect, is dissolving.
We are watching perhaps the most engaging act in our history. Amid the powerful purr of particle accelerators, the click of computer printouts, and dancing instrument gauges, the old “science” that has given us so much, including our sense of helplessness before the faceless forces of bigness, is undermining its own foundations.
With the awesome authority that we have given it, science is telling us that our faith has been misplaced. It appears that we have attempted the impossible, to disown our part in the universe. We have tried to do this by relinquishing our authority to the Scientists. To the Scientists we gave the responsibility of probing the mysteries of creation, change, and death. To us we gave the everyday routine of mindless living.
The Scientists readily assumed their task. We readily assumed ours, which was to play a role of impotence before the ever-increasing complexity of “modern science” and the ever-spreading specialization of modern technology.
Now, after three centuries, the Scientists have returned with their discoveries. They are as perplexed as we are (those of them who have given thought to what is happening).
“We are not sure,” they tell us, “but we have accumulated evidence which indicates that the key to understanding the universe is you.”
This is not only different from the way that we have looked at the world for three hundred years, it is opposite. The distinction between the “in here” and the “out there” upon which science was founded, is becoming blurred. This is a puzzling state of affairs. Scientists, using the “in here—out there” distinction, have discovered that the “in here—out there” distinction may not exist! What is “out there” apparently depends, in a rigorous mathematical sense as well as a philosophical one, upon what we decide “in here”.
The new physics tells us that an observer cannot observe without altering what he sees. Observer and observed are interrelated in a real and fundamental sense. The exact nature of this interrelation is not clear, but there is a growing body of evidence that the distinction between the “in here” and the “out there” is illusion.
The conceptual framework of quantum mechanics, supported by massive volumes of experimental data, forces contemporary physicists to express themselves in a manner that sounds, even to the uninitiated, like the language of mystics.
Access to the physical world is through experience. The common denominator of all experiences is the “I” that does the experiencing. In short, what we experience is not external reality, but our interaction with it. This is a fundamental assumption of “complementarity”.
Complementarity is the concept developed by Niels Bohr to explain the wave-particle duality of light. No one has thought of a better one yet. Wave-like characteristics and particle-like characteristics, the theory goes, are mutually exclusive, or complementary aspects of light. Although one of them always excludes the other, both of them are necessary to understand light. One of them always excludes the other because light, or anything else, cannot be both wave-like and particle-like at the same time.fn1
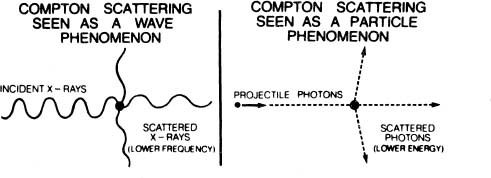
How can mutually exclusive wave-like and particle-like behaviors both be properties of one and the same light? They are not properties of light. They are properties of our interaction with light. Depending upon our choice of experiment, we can cause light to manifest either particle-like properties or wave-like properties. If we choose to demonstrate the wave-like characteristics of light, we can perform the double-slit experiment which produces interference. If we choose to demonstrate the particle-like characteristics of light, we can perform an experiment which illustrates the photoelectric effect. We can cause light to manifest both wave-like properties and particle-like properties by performing Arthur Compton’s famous experiment.
In 1923, Compton played the world’s first game of billiards with subatomic particles, and, in the process, confirmed Einstein’s seventeen-year-old photon theory of light. His experiment was not conceptually difficult. He simply fired x-rays, which everybody knows are waves, at electrons. To the surprise of most people, the x-rays bounced off the electrons as if they (the x-rays) were particles! For example, the x-rays which struck the electrons glancing blows were deflected only slightly from their paths. They did not lose much energy in the collision. However, those x-rays which collided more nearly head-on with electrons were deflected sharply. These x-rays lost a considerable amount of their kinetic energy (the energy of motion) in the collision.
Compton could tell just how much energy the deflected x-rays lost by measuring their frequencies before and after the collision. The frequencies of those x-rays involved in near head-on collisions were noticeably lower after the collision than before it. This meant that they had less energy after the collision than they had before the collision. Compton’s x-rays were impacting with electrons exactly the way that billiard balls impact with other billiard balls.

Compton’s discovery was intimately related to quantum theory. Compton could not have revealed the particle-like behavior of x-rays if Planck had not discovered his fundamental rule that higher frequency means higher energy. This rule permitted Compton to prove that the x-rays in his experiment lost energy in a particle-like collision (because their frequencies were lower after the collision than before the collision).
The conceptual paradox in Compton’s experiment shows how deeply the wave-particle duality is embedded in quantum mechanics. Compton proved that electromagnetic radiations, like x-rays, have particle-like characteristics by measuring their frequencies! Of course, “particles” don’t have frequencies. Only waves have frequencies. The phenomenon which Compton discovered is called Compton scattering, in honor of what happens to the x-rays.
In short, we can demonstrate that light is particle-like with the photoelectric effect, that it is wave-like with the double-slit experiment, and that it is both particle-like and wave-like with Compton scattering. Both of these complementary aspects of light (wave and particle) are necessary to understand the nature of light. It is meaningless to ask which one of them, alone, is the way light really is. Light behaves like waves or like particles depending upon which experiment we perform.
The “we” that does the experimenting is the common link that connects light as particles and light as waves. The wave-like behavior that we observe in the double-slit experiment is not a property of light, it is a property of our interaction with light. Similarly, the particle-like characteristics that we observe in the photoelectric effect are not a property of light. They, too, are a property of our interaction with light. Wave-like behavior and particle-like behavior are properties of interactions.
Since particle-like behavior and wave-like behavior are the only properties that we ascribe to light, and since these properties now are recognized to belong (if complementarity is correct) not to light itself, but to our interaction with light, then it appears that light has no properties independent of us! To say that something has no properties is the same as saying that it does not exist. The next step in this logic is inescapable. Without us, light does not exist.
Transferring the properties that we usually ascribe to light to our interaction with light deprives light of an independent existence. Without us, or by implication, anything else to interact with, light does not exist. This remarkable conclusion is only half the story. The other half is that, in a similar manner, without light, or, by implication, anything else to interact with, we do not exist! As Bohr himself put it:
. . . an independent reality in the ordinary physical sense can be ascribed neither to the phenomena nor to the agencies of observation.1
By “agencies of observation”, he may have been referring to instruments, not people, but philosophically, complementarity leads to the conclusion that the world consists not of things, but of interactions. Properties belong to interactions, not to independently existing things, like “light”. This is the way that Bohr solved the wave-particle duality of light. The philosophical implications of complementarity became even more pronounced with the discovery that the wave-particle duality is a characteristic of everything.
When we left off telling the story of quantum mechanics, the tale had progressed as follows: In 1900, Max Planck, studying black-body radiation, discovered that energy is absorbed and emitted in chunks, which he called quanta. Until that time, radiated energy, like light, was thought to be wave-like. This was because Thomas Young, in 1803, showed that light produces interference (the double-slit experiment), and only waves can do that.
Einstein, stimulated by Plank’s discovery of quanta, used the photoelectric effect to illustrate his theory that not only are the processes of energy absorption and emission quantized, but that energy itself comes in packages of certain sizes. Thus physicists were confronted with two sets of experiments (repeatable experiences) each of which seemed to disprove the other other. This is the famous wave-particle duality which is fundamental to quantum mechanics.
While physicists were trying to explain how waves can be particles, a young French prince, Louis de Broglie, dropped a bomb which demolished what was left of the classical view. Not only are waves particles, he proposed, but particles are also waves!
De Broglie’s idea (which was contained in his doctoral thesis) was that matter has waves which “correspond” to it. The idea was more than philosophical speculation. It was also mathematical speculation. Using the simple equations of Planck and Einstein, de Broglie formulated a simple equation of his own.fn2 It determines the wavelength of the “matter waves” that “correspond” to matter. It says simply that the greater the momentum of a particle, the shorter is the length of its associated wave.
This explains why matter waves are not evident in the macroscopic world. De Broglie’s equation tells us that the matter waves corresponding to even the smallest object that we can see are so incredibly small compared to the size of the object that their effect is negligible. However, when we get down to something as small as a subatomic particle, like an electron, the size of the electron itself is smaller than the length of its associated wave!
Under these circumstances, the wave-like behavior of matter should be clearly evident, and matter should behave differently than “matter” as we are used to thinking of it. This is exactly what happens.
Only two years after de Broglie presented this hypothesis, an experimenter named Clinton Davisson, working with his assistant, Lester Germer, at the Bell Telephone Laboratories, verified it experimentally. Both Davisson and de Broglie got Nobel Prizes, and physicists were left to explain not only how waves can be particles, but also how particles can be waves.
The famous Davisson-Germer experiment, which was done by accident, showed electrons reflecting off a crystal surface in a manner that could be explained only if the electrons were waves. But, of course, electrons are particles.
Today, electron diffraction, an apparent contradiction in terms, is a common phenomenon. When a beam of electrons is sent through tiny openings, like the spaces between the atoms in a metal foil, which are as small or smaller than the wavelengths of the electrons (isn’t this ridiculous—“particles” don’t have wavelengths!), the beam diffracts exactly the way a beam of light diffracts. Although, classically speaking, it can’t happen, here is a picture of it.
It was disconcerting enough when light, which is made of waves, began to behave like particles, but when electrons, which are particles, began to behave like waves, the plot became unbearably thick.
The unfolding of quantum mechanics was (and still is) a drama of high suspense. Werner Heisenberg wrote:
I remember discussions with Bohr [in 1927] which went through many hours till very late at night and ended almost in despair; and when at the end of the discussion I went alone for a walk in the neighboring park I repeated to myself again and again the question: Can nature possibly be as absurd as it seemed to us in these atomic experiments.2
Subsequent experiments were to reveal that not only subatomic particles, but atoms and molecules as well have associated matter waves. The title of Donald Hughes’ pioneer book, Neutron Optics, provides eloquent testimony of the merger between waves and particles to which Prince de Broglie’s doctoral thesis gave birth. Theoretically, in fact, everything has a wavelength—baseballs, automobiles, and even people—although their wavelengths are so small that they are not noticeable.
De Broglie himself was not very helpful in explaining his theory. It predicted what the Davisson-Germer experiment proved: that matter, like electrons, has a wave-like aspect. His equation even foretold the wavelength of these waves. Nonetheless, no one knew what these waves actually were (no one does yet). De Broglie called them waves which “correspond” to matter, but he did not explain what “correspond” meant.
Is it possible for a physicist to predict something, calculate equations which describe it, and still not know what he is talking about?
Yes. As Bertrand Russell put it:
Mathematics may be defined as the subject in which we never know what we are talking about, nor whether what we are saying is true.3
This is why the physicists at Copenhagen decided to accept quantum mechanics as a complete theory even though it gives no explanation of what the world is “really like”, and even though it predicts probabilities and not actual events. They accepted quantum mechanics as a complete theory because quantum mechanics correctly correlates experience. Quantum mechanics, and, according to the pragmatists, all science, is the study of correlations between experiences. De Broglie’s equation correctly correlates experiences.
De Broglie merged the wave-particle paradox which came to light through the genius of Thomas Young (double-slit experiment) and Albert Einstein (photon theory). In other words, he connected the two most revolutionary phenomena of physics, the quantum nature of energy and the wave-particle duality.
De Broglie presented his matter-wave theory in 1924. During the next three years quantum mechanics crystallized into what it essentially is today. The world of Newtonian physics, simple mental pictures, and common sense disappeared. A new physics took form with an originality and force that left the mind reeling.
After de Broglie’s matter waves came the Schrödinger wave equation.
De Broglie’s matter waves seemed to Erwin Schrödinger, the Viennese physicist, a much more natural way of looking at atomic phenomena than Bohr’s planetary model of the atom. Bohr’s model of hard, spherical electrons revolving around a nucleus at specific levels and emitting photons by jumping from one level to another explained the color spectrum of simple atoms, but it said nothing about why each shell contains only a certain number of electrons, no more and no less. It also did not explain how the electrons do their jumping (for example, what is happening to them between shells).fn4
Stimulated by de Broglie’s discovery, Schrödinger hypothesized that electrons are not spherical objects, but patterns of standing waves.
Standing waves are familiar phenomena to anyone who has played with a clothesline. Suppose that we tie one end of a rope to a pole, and then pull it tight. On this rope there are no waves at all, either standing or traveling. Now suppose that we flick our wrist sharply downward and then upward. A hump appears in the rope and travels down the rope to the pole where it turns upside down and returns to our hand. This traveling hump (figure A) is a traveling wave. By sending a series of humps down the rope, we can set up the patterns of standing waves shown below, and more that are not shown.
The simplest of these is the pattern shown in figure B. This pattern is formed by the superposition of two traveling waves, a direct one and a reflected one traveling in the opposite direction. It is the pattern, not the rope, which does not move. The widest point in the standing wave remains “stationary”, and so do the points at the ends of the standing wave. These points are called nodes. There are two of them in the simplest standing pattern, one at our hand and one at the pole where the rope is attached. These stationary patterns, superpositions of traveling waves, are called standing waves.
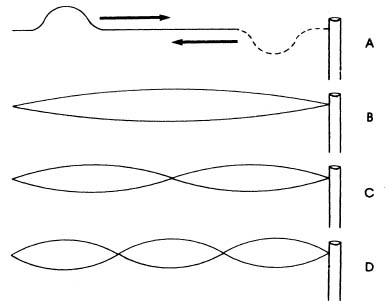
No matter how long or short our rope is, there can be only a whole number of standing waves on it. That is, it can have a pattern of one standing wave, or a pattern of two standing waves, or a pattern of three, four, five, and so on, standing waves, but it can never have a pattern of one and one half standing waves, or a pattern of two and one fourth standing waves. The standing waves must divide the rope evenly into whole sections. Another way to say this is that we can increase or decrease the number of standing waves on a rope only by a whole number of them. This means that the only way that the number of standing waves on a rope can increase or decrease is discontinuously!
Furthermore, standing waves on a rope cannot be just any size. They always will be restricted to those lengths which divide the rope evenly. The actual size of the waves depends upon how long the rope is, but no matter what length the rope, there will be only certain lengths which divide it evenly.
All of this was old stuff in 1925. Plucking a guitar string establishes patterns of standing waves on it. Blowing air into an organ pipe creates standing wave patterns in it. What was new was Schrödinger’s realization that standing waves are “quantized” the same way that atomic phenomena are! In fact, Schrödinger proposed that electrons are standing waves.
In retrospect, this is not as fantastic as it first sounds. At the time, however, it was a stroke of genius. Picture an electron in orbit around a nucleus. Each time the electron completes a journey around the nucleus, it travels a certain distance. That distance is a certain length, like our rope was a certain length. Similarly, only a whole number of standing waves, never a fraction of one, can form in this length. (Length of what is an unanswered question).
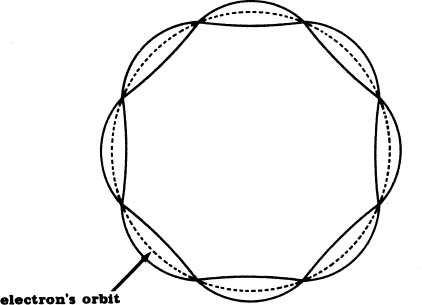
Schrödinger proposed that each of these standing waves is an electron! In other words, he proposed that electrons are the segments of vibrations bounded by the nodes.
So far, we have talked about standing waves on a line, like a clothesline or a guitar string, but standing waves also occur in other mediums, like water. Suppose that we throw a rock into a round pool. Waves radiate from its point of entry. These waves are reflected, sometimes more than once, off different sides of the pool. When the reflected traveling waves interfere with each other they create a complex pattern of standing waves which is our old friend, interference.
Where the crest of one wave meets the trough of another wave, they cancel each other and the surface of the water along this line of interaction is calm. These calm areas are the nodes which separate the standing waves. In the double-slit experiment, the nodes are the dark bands in the pattern of alternating light and dark areas. The light bands are the crests of the standing waves.
Schrödinger chose the model of a small tub of water with its complex and intricate interference pattern to explain the nature of the atom. This model is, as he put it, an “analogue” of electron waves in an atom-sized basin.
The ingenious but nevertheless somewhat artificial assumptions of [Bohr’s model of the atom] . . . are replaced by a much more natural assumption in de Broglie’s wave phenomena. The wave phenomenon forms the real “body” of the atom. It replaces the individual punctiform [pointlike] electrons, which in Bohr’s model swarm around the nucleus.4
Standing waves on clotheslines have two dimensions: length and width. Standing waves in mediums like water, or on the head of a conga drum, have three dimensions: length, width, and depth. Schrödinger analyzed the standing wave patterns of the simplest atom, hydrogen, which has only one electron. In hydrogen alone he calculated, using his new wave equation, a multitude of different possible shapes of standing waves. All of the standing waves on a rope are identical. This is not true of the standing waves in an atom. All of them are three-dimensional and all of them are different. Some of them look like concentric circles. Some of them look like butterflies, and others look like mandalas (next page).
Shortly before Schrödinger’s discovery, another Austrian physicist, Wolfgang Pauli, discovered that no two electrons in an atom can be exactly alike. The presence of an electron with one particular set of properties (“quantum numbers”) excludes the presence of another electron with exactly the same properties (quantum numbers) within the same atom. For this reason, Pauli’s discovery became known as the Pauli exclusion principle. In terms of Schrödinger’s standing wave theory, Pauli’s exclusion principle means that once a particular wave pattern forms in an atom, it excludes all others of its kind.
Schrödinger’s equation, modified by Pauli’s discovery, shows that there are only two possible wave patterns in the lowest of Bohr’s energy levels, or shells. Therefore, there can be only two electrons in it. There are eight different standing-wave patterns possible in the next energy level, therefore there can be only eight electrons in it, and so on.
These are exactly the numbers of electrons that Bohr’s model assigns to these energy levels. In this respect, the two models are alike. In another important way, however, they are different.
Bohr’s theory was entirely empirical. That is, he built it around the experimentally observed facts to explain them. In contrast, Schrödinger built his theory on de Broglie’s matter-wave hypothesis. Not only does it yield mathematical values which have been verified experimentally, but it also provides a consistent explanation for them.
For example, there are only a certain number of electrons in each energy level, because there are only a certain number of standing wave patterns possible at each energy level. The energy level of an atom jumps only from certain specific values to other certain specific values, because standing-wave patterns of only certain dimensions can form with the atom, and none other.
Although Schrödinger was sure that electrons were standing waves, he was not sure what was waving.fn7 He was convinced, nonetheless, that something was waving, and he called it psi a Greek letter pronounced “sigh”. (A “wave function” and a “psi function” are the same thing).
To use the Schrödinger wave equation, we feed it certain characteristics of the atom in question. It then gives us the evolution in time of standing-wave patterns which occur in the atom. If we prepare an atom in an initial state and let it propagate in isolation, that initial state, while propagating in isolation, evolves in time into different standing-wave patterns. The order of these patterns is calculable. The Schrödinger wave equation is the mathematical device which physicists use to calculate the order of these patterns. Said another way, the development of standing wave patterns in an atom is deterministic. Given initial conditions, one pattern always follows another in accordance with the Schrödinger wave equation.fn8
The Schrödinger wave equation also provides a self-consistent explanation of the size of the hydrogen atom. According to it, the wave pattern of a system with one electron and one proton, which is what we call a hydrogen atom, in its lowest energy state, has an appreciable magnitude only within a sphere which is just the diameter of the smallest Bohr orbit. In other words, such a wave pattern turns out to be the same size as the ground state of a hydrogen atom!
Although Schrödinger’s wave mechanics became a pillar of today’s quantum mechanics, the useful aspects of Bohr’s model of subatomic phenomena still are used when the wave theory does not yield appropriate results. In such cases, physicists simply stop thinking in terms of standing waves and start thinking again in terms of particles. No one can say that they are not adaptable in this matter (wave).
Schrödinger was convinced that his equations described real things, and not mathematical abstractions. He pictured electrons as actually being spread out over their wave patterns in the form of a tenuous cloud. If the picture is limited to the one-electron hydrogen atom, whose standing waves have only three dimensions (length, width, and depth), this is possible to imagine. However, the standing waves in an atom with two electrons exist in six mathematical dimensions; the standing waves in an atom with four electrons exist in twelve dimensions, etc. To visualize this is quite an exercise.
At this point Max Born, a German physicist, put the final touch to the new wave interpretation of subatomic phenomena. According to him, it is not necessary or possible to visualize these waves because they are not real things, they are probability waves.
. . . the whole course of events is determined by the laws of probability; to a state in space there corresponds a definite probability, which is given by the de Broglie wave associated with the state.5
To obtain the probability of a given state we square (multiply by itself) the amplitude of the matter wave associated with the state.
The question of whether de Broglie’s equations and Schrödinger’s equations represent real things or abstractions was clear to Born. It did not make sense to him to try to think of a real thing that exists in more than three dimensions.
We have two possibilities. Either we use waves in spaces of more than three dimensions . . . or we remain in three-dimensional space, but give up the simple picture of the wave amplitude as an ordinary physical magnitude, and replace it by a purely abstract mathematical concept . . . into which we cannot enter.6
This is exactly what he did. “Physics,” he wrote,
is in the nature of the case indeterminate, and therefore the affair of statistics.7
This is the same idea (probability waves) that Bohr, Kramers, and Slater had thought of earlier. This time, however, using the mathematics of de Broglie and Schrödinger, the numbers came out right.
Born’s contribution to Schrödinger’s theory is what enables quantum mechanics to predict probabilities. Since the probability of a state is found by squaring the amplitude of the matter wave associated with it, and, given initial conditions, the Schrödinger equation predicts the evolution of these wave patterns, the two taken together give a determinable evolution of probabilities. Given any initial state, physicists can predict the probability that an observed system will be observed to be in any other given state at any particular time. Whether or not the observed system is observed to be in that state, however, even if that state is the most probable state for that time, is a matter of chance. In other words, the “probability” of quantum mechanics is the probability of observing an observed system in a given state at a given time if it was prepared in a given initial state.fn9
Thus it was that the wave aspect of quantum mechanics developed. Just as waves have particle-like characteristics (Planck, Einstein), particles also have wave-like characteristics (de Broglie). In fact, particles can be understood in terms of standing waves (Schrödinger). Given initial conditions, a precise evolution of standing-wave patterns can be calculated via the Schrödinger wave equation. Squaring the amplitude of a matter wave (wave function) gives the probability of the state that corresponds to that wave (Born). Therefore, a sequence of probabilities can be calculated from initial conditions by using the Schrödinger wave equation and Born’s simple formula.
We have come a long way from Galileo’s experiments with falling bodies. Each step along the path has taken us to a higher level of abstraction: first to the creation of things that no one has ever seen (like electrons), and then to the abandonment of all attempts even to picture our abstractions.
The problem is, however, that human nature being what it is, we do not stop trying to picture these abstractions. We keep asking “What are these abstractions of?”, and then we try to visualize whatever that is.
Earlier we dismissed Bohr’s planetary model of the atom with the promise that we later would see “how physicists currently think of an atom”. Well, the time has come, but the task is a thorny one. We gave up our old picture of the atom so easily because we assumed that it would be replaced by one more meaningful, but equally as lucid. Now it develops that our replacement picture is not a picture at all, but an unvisualizable abstraction. This is uncomfortable because it reminds us that atoms were never “real” things anyway. Atoms are hypothetical entities constructed to make experimental observations intelligible. No one, not one person, has ever seen an atom. Yet we are so used to the idea that an atom is a thing that we forget that it is an idea. Now we are told that not only is an atom an idea, it is an idea that we cannot even picture.
Nonetheless, when physicists refer to mathematical entities in English (or German or Danish), the words that they use are bound to create images for laymen who hear them, but who are not familiar with the mathematics to which they refer. Therefore, given this lengthy explanation of why it cannot be done, we come now to how physicists today picture an atom.
An atom consists of a nucleus and electrons. The nucleus is located at the center of the atom. It occupies only a small part of the atom’s volume, but almost all of its mass. This is the same nucleus as in the planetary model. As in the planetary model, electrons move in the general area of the nucleus. In this model, however, the electrons may be anywhere within an “electron cloud”. The electron cloud is made of various standing waves which surround the nucleus. These standing waves are not material. They are patterns of potential. The shape of the various standing waves which comprise the electron cloud tells physicists the probability of finding the point electron at any given place in the cloud.
In short, physicists still think of an atom as a nucleus around which move electrons, but the picture is not so simple as that of a tiny solar system. The electron cloud is a mathematical concept which physicists have constructed to correlate their experiences. Electron clouds may or may not exist within an atom. No one really knows. However, we do know that the concept of an electron cloud yields the probabilities of finding the electron at various places around the nucleus of an atom, and that these probabilities have been determined empirically to be accurate.
In this sense, electron clouds are like wave functions. A wave function also is a mathematical concept which physicists have constructed to correlate their experiences. Wave functions may or may not “actually exist”. (This type of statement assumes a qualitative difference between thought and matter, which may not be a good assumption). However, the concept of a wave function undeniably yields the probabilities of observing a system to be in a given state at a given time if it was prepared in a given way.
Like wave functions, electron clouds generally cannot be visualized. An electron cloud containing only one electron (like the electron cloud of a hydrogen atom) exists in three dimensions. All other electron clouds, however, contain more than one electron and therefore exist in more than three dimensions. The nucleus of the simple carbon atom, for example, with its six electrons, is surrounded by an electron cloud with eighteen dimensions. Uranium, with ninety-two electrons, has an electron cloud of 276 dimensions. (Similarly, a wave function contains three dimensions for each possibility that it represents). The situation, in terms of mental pictures, is clearly unclear.
This ambiguity results from attempting to depict with limited concepts (language) situations which are not bound by the same limitations. It also masks the fact that we do not know what actually is going on in the invisible subatomic realm. The models that we use are “free creations of the human mind”, to use Einstein’s words (see here), that satisfy our innate need to correlate experience rationally. They are guesses about what “really” goes on inside the unopenable watch. It is extremely misleading to think that they actually describe anything.
In fact, a young German physicist, Werner Heisenberg, decided that we never can know what actually goes on in the invisible subatomic realm, and that, therefore, we should “abandon all attempts to construct perceptual models of atomic processes.”8 All that we legitimately can work with, according to this theory, is what we observe directly. All we know is what we have at the beginning of an experiment, and what we have at the end of it. Any explanation of what actually happens between these two states—which are the observables (see here)—is speculation.
Therefore, about the same time (1925), but independently of de Broglie and Schrödinger, the twenty-five-year-old Heisenberg set about developing a means of organizing experimental data into tabular form. He was fortunate in that sixty-six years earlier an Irish mathematician named W. R. Hamilton had developed a method of organizing data into arrays, or mathematical tables, called matrices. At that time, Hamilton’s matrices were considered the fringe of pure mathematics. Who could have guessed that one day they would fit, like a precut piece, into the structure of a revolutionary physics?
To use Heisenberg’s tables, we simply read from them, or calculate from them, what probabilities are associated with what initial conditions. Using this method, which Heisenberg called matrix mechanics, we deal only with physical observables, which means those things that we know at the beginning of an experiment, and those things that we know about it at the end. We make no speculation about what happens in between.
After twenty-five years of struggling for a theory to replace Newtonian physics, physicists suddenly found themselves with two different theories, each one a unique way of approaching the same thing: Schrödinger’s wave mechanics, based on de Broglie’s matter waves, and Heisenberg’s matrix mechanics, based on the unanalyzability of subatomic phenomena.
Within a year after Heisenberg developed his matrix mechanics, Schrödinger discovered that it was mathematically equivalent to his own wave mechanics. Since both of these theories were valuable tools for subatomic research, both of them were incorporated into the new branch of physics which became known as quantum mechanics.
Much later, Heisenberg applied matrix mathematics to the particle collision experiments of high-energy particle physics. Because such collisions always result in a scattering of particles, it was called the Scattering Matrix, which was shortened to the S Matrix. Today, physicists have two ways to calculate the transition probabilities between what they observe at the beginning of a quantum mechanical experiment and what they observe at the end of it.
The first method is the Schrödinger wave equation, and the second method is the S Matrix. The Schrödinger wave equation describes a temporal development of possibilities, one of which suddenly actualizes when we make a measurement in the course of a quantum mechanical experiment. The S Matrix gives directly the transition probabilities between the observables without giving any indication of a development in time, or the lack of it, or anything else. Both of them work.fn10
As important as was Heisenberg’s introduction of matrix mathematics into the new physics, his next discovery shook the very foundations of “the exact sciences”. He proved that, at the subatomic level, there is no such thing as “the exact sciences”.
Heisenberg’s remarkable discovery was that there are limits beyond which we cannot measure accurately, at the same time, the processes of nature. These limits are not imposed by the clumsy nature of our measuring devices or the extremely small size of the entities that we attempt to measure, but rather by the very way that nature presents itself to us. In other words, there exists an ambiguity barrier beyond which we never can pass without venturing into the realm of uncertainty. For this reason, Heisenberg’s discovery became known as the “uncertainty principle”.
The uncertainty principle reveals that as we penetrate deeper and deeper into the subatomic realm, we reach a certain point at which one part or another of our picture of nature becomes blurred, and there is no way to reclarify that part without blurring another part of the picture! It is as though we are adjusting a moving picture that is slightly out of focus. As we make the final adjustments, we are astonished to discover that when the right side of the picture clears, the left side of the picture becomes completely unfocused and nothing in it is recognizable. When we try to focus the left side of the picture, the right side starts to blur and soon the situation is reversed. If we try to strike a balance between these two extremes, both sides of the picture return to a recognizable condition, but in no way can we remove the original fuzziness from them.
The right side of the picture, in the original formulation of the uncertainty principle, corresponds to the position in space of a moving particle. The left side of the picture corresponds to its momentum. According to the uncertainty principle, we cannot measure accurately, at the same time, both the position and the momentum of a moving particle. The more precisely we determine one of these properties, the less we know about the other. If we precisely determine the position of the particle, then, strange as it sounds, there is nothing that we can know about its momentum. If we precisely determine the momentum of the particle, there is no way to determine its position.
To illustrate this strange statement, Heisenberg proposed that we imagine a super microscope of extraordinarily high resolving power—powerful enough, in fact, to be able to see an electron moving around in its orbit. Since electrons are so small, we cannot use ordinary light in our microscope because the wavelength of ordinary light is much too long to “see” electrons, in the same way that long sea waves barely are influenced by a thin pole sticking out of the water.
If we hold a strand of hair between a bright light and the wall, the hair casts no distinct shadow. It is so thin compared to the wavelengths of the light that the light waves bend around it instead of being obstructed by it. To see something, we have to obstruct the light waves we are looking with. In other words, to see something, we have to illuminate it with wavelengths smaller than it is. For this reason, Heisenberg substituted gamma rays for visible light in his imaginary microscope. Gamma rays have the shortest wavelength known, which is just what we need for seeing an electron. An electron is large enough, compared to the tiny wavelength of gamma rays, to obstruct some of them: to make a shadow on the wall, as it were. This enables us to locate the electron.
The only problem, and this is where quantum physics enters the picture, is that, according to Planck’s discovery, gamma rays, which have a much shorter wavelength than visible light, also contain much more energy than visible light. When a gamma ray strikes the imaginary electron, it illuminates the electron, but unfortunately, it also knocks it out of its orbit and changes its direction and speed (its momentum) in an unpredictable and uncontrollable way. (We cannot calculate precisely the angle of rebound between a particle, like the electron, and a wave, like the gamma ray). In short, if we use light with a wavelength short enough to locate the electron, we cause an undeterminable change in the electron’s momentum.
The only alternative is to use a less energetic light. Less energetic light, however, causes our original problem: Light with an energy low enough not to disturb the momentum of the electron will have a wavelength so long that it will not be able to show us where the electron is! There is no way that we can know simultaneously the position and the momentum of a moving particle. All attempts to observe the electron alter the electron.
This is the primary significance of the uncertainty principle. At the subatomic level, we cannot observe something without changing it. There is no such thing as the independent observer who can stand on the sidelines watching nature run its course without influencing it.
In one sense, this is not such a surprising statement. A good way to make a stranger turn and look at you is to stare intently at his back. All of us know this, but we often discredit what we know when it contradicts what we have been taught is possible. Classical physics is based on the assumption that our reality, independently of us, runs its course in space and time according to strict causal laws. Not only can we observe it, unnoticed, as it unfolds, we can predict its future by applying causal laws to initial conditions. In this sense, Heisenberg’s uncertainty principle is a very surprising statement.
We cannot apply Newton’s laws of motion to an individual particle that does not have an initial location and momentum, which is exactly what the uncertainty principle shows us that we cannot determine. In other words, it is impossible, even in principle, ever to know enough about a particle in the subatomic realm to apply Newton’s laws of motion which, for three centuries, were the basis of physics. Newton’s laws do not apply to the subatomic realm.fn11 (Newton’s concepts do not even apply in the subatomic realm). Given a beam of electrons, quantum theory can predict the probable distribution of the electrons over a given space at a given time, but quantum theory cannot predict, even in principle, the course of a single electron. The whole idea of a causal universe is undermined by the uncertainty principle.
In a related context, Niels Bohr wrote that quantum mechanics, by its essence, entails:
. . . the necessity of a final renunciation of the classical ideal of causality and a radical revision of our attitude toward the problem of physical reality.9
Yet there is another startling implication in the uncertainty principle. The concepts of position and momentum are intimately bound up with our idea of a thing called a moving particle. If, as it turns out, we cannot determine the position and momentum of a moving particle, as we always have assumed that we could, then we are forced to admit that this thing that we have been calling a moving particle, whatever it is, is not the “moving particle” we thought it was, because “moving particles” always have both position and momentum.
As Max Born put it:
. . . if we can never actually determine more than one of the two properties (possession of a definite position and of a definite momentum), and if when one is determined we can make no assertion at all about the other property for the same moment, so far as our experiment goes, then we are not justified in concluding that the “thing” under examination can actually be described as a particle in the usual sense of the term.10
Whatever it is that we are observing can have a determinable momentum, and it can have a determinable position, but of these two properties, we must choose, for any given moment, which one we wish to bring into focus. This means, in reference to “moving particles” anyway, that we can never see them the way they “really are”, but only the way we choose to see them!
As Heisenberg wrote:
What we observe is not nature itself, but nature exposed to our method of questioning.11
The uncertainty principle rigorously brings us to the realization that there is no “My Way” which is separate from the world around us. It brings into question the very existence of an “objective” reality, as does complementarity and the concept of particles as correlations.
The tables have been turned. “The exact sciences” no longer study an objective reality that runs its course regardless of our interest in it or not, leaving us to fare as best we can while it goes its predetermined way. Science, at the level of subatomic events, is no longer exact, the distinction between objective and subjective has vanished, and the portals through which the universe manifests itself are, as we once knew a long time ago, those impotent, passive witnesses to its unfolding, the “I”s, of which we, insignificant we, are examples. The Cogs in the Machine have become the Creators of the Universe.
If the new physics has led us anywhere, it is back to ourselves, which, of course, is the only place that we could go.
fn1 Individual events are always particle-like; wave behavior is detected as a statistical pattern, i.e., interference. However, in the words of Paul Dirac (another founder of quantum mechanics) even a single subatomic particle “interferes with itself”. How a single subatomic particle, like an electron, for example, can “interfere with itself” is the basic quantum paradox.
fn2 Planck’s equation: E = hʋ. Einstein’s equation: E = mc2. De Broglie’s equation: λ = h/mv.
fn3 As you hold this photograph in front of you, the beam of electrons (the “transmitted beam”) is coming directly toward you out of the large white spot in the center. Also located in the white spot is the diffracting material (in this case, the electron beam is being diffracted by small grains of gold, i.e., the beam is being directed through a thin polycrystalline gold foil). The rings on the photograph mark the places where the diffracted electron beams struck the film which was placed on the opposite side of the gold foil from the electron source. The white spot in the center of the photograph was caused by undiffracted electrons in the transmitted beam passing through the gold foil and striking the film directly.
fn4 Accurately speaking, Schrödinger’s theory does not explain The Jump, either. In fact, Schrödinger did not like the idea of a “jump”.
fn5 These photographs are of mechanical simulations of probability density distributions of different electron states in the hydrogen atom. In other words, they represent where we are most likely to find the point-like electron when we look for it if the atom is in this or that particular state (there are more states than those shown). Initially, Schrödinger pictured electrons as being tenuous clouds actually assuming these patterns.
fn6 A “quantum jump” can be thought of as a transition from one of these pictures to another without anything in between.
fn7 Schrödinger’s early interpretation that electrons literally were standing waves did not stand up to detailed examination and he had to renounce it. Soon, however, the concept of probability based upon a wave function representing an observed system (and developing according to the Schrödinger wave equation) became a fundamental tool in atomic research and Schrödinger’s famous equation became an integral part of quantum theory. Since the Schrödinger wave equation is non-relativistic, however, it does not work at high energies. Therefore, high-energy particle physicists usually use the S Matrix to calculate transition probabilities. (S Matrix theory is discussed in a later chapter).
fn8 Until the propagating system interacts with a measuring device. That causes an abrupt, unpredictable transition to another state (a quantum jump).
fn9 If the state is prepared in state Ψ(t), the probability that it will be observed to be in state ϕ(t) is | < Ψ(t)| ϕ(t) > |2. If it is prepared in state Ψ(t) then the probability that it will be observed in region Δ at time t is ![]()
fn10 The Schrödinger wave equation works at lower energies, however, since it is nonrelativistic, it does not work for high energies. Therefore, most particle physicists use the S Matrix together, perhaps, with local relativistic quantum fields.
fn11 Strictly speaking, Newton’s laws do not disappear totally in the subatomic realm: they remain valid as operator equations. Also, in some experiments involving subatomic particles Newton’s laws may be taken as good approximations in the description of what is happening.