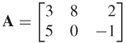
A matrix is a collection of numbers ordered by rows and columns. It is customary to enclose the elements of a matrix in parentheses, brackets, or braces. For example, the following is a matrix:
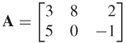
This matrix has two rows and three columns, so it is referred to as a 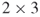 matrix. The elements of a matrix are numbered in the following way:
matrix. The elements of a matrix are numbered in the following way:
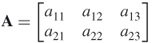
That is, the first subscript in a matrix element refers to the row that the element resides, and the second subscript refers to the column. It is important to remember this convention when matrix algebra is performed.
A vector is a special type of matrix that has only one row (called a row vector) or one column (called a column vector). Below, B is a column vector whereas C is a row vector.
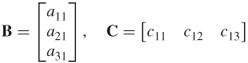
A scalar is a matrix with only one row and one column. It is customary to denote scalars by italicized, lower case letters (e.g., a), to denote vectors by bold, lower case letters (e.g., a), and to denote matrices with more than one row and one column by bold, upper case letters (e.g., A).
A square matrix has as many rows as it has columns. Matrix A is square but matrix B is not square:
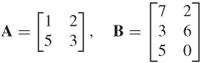
A symmetric matrix is a square matrix in which 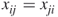 for all
for all 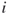 and
and 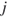 . Matrix A is symmetric; matrix B is not symmetric.
. Matrix A is symmetric; matrix B is not symmetric.
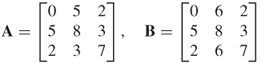
A diagonal matrix is a symmetric matrix where all the off diagonal elements are  . Matrix A is diagonal.
. Matrix A is diagonal.
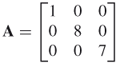
An identity matrix is a diagonal matrix with 1s and only 1s on the diagonal. The identity matrix is almost always denoted as I.
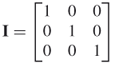
To add two matrices, they both must have the same number of rows and they both must have the same number of columns. The elements of the two matrices are simply added together, element by element, to produce the results. That is, for R = A + B, then
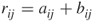
for all 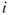 and
and 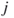 . Thus,
. Thus,
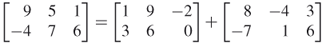
Matrix subtraction works in the same way, except that elements are subtracted instead of added.
There are several rules for matrix multiplication. The first concerns the multiplication between a matrix and a scalar. Here, each element in the product matrix is simply the scalar multiplied by the element in the matrix. That is, for R = aB, then
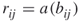
for all 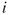 and
and 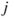 . Thus,
. Thus,
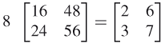
Matrix multiplication involving a scalar is commutative. That is, aB = Ba.
The next rule involves the multiplication of a row vector by a column vector. To perform this, the row vector must have as many columns as the column vector has rows. For example,
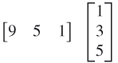
is legal. However,
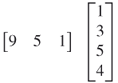
is not legal because the row vector has three columns, whereas the column vector has four rows. The product of a row vector multiplied by a column vector will be a scalar. This scalar is simply the sum of the first row vector element multiplied by the first column vector element plus the second row vector element multiplied by the second column vector element plus the product of the third elements, etc. In algebra, if 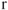 = ab, then
= ab, then
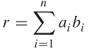
Thus,
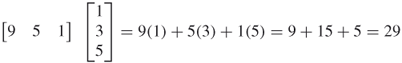
All other types of matrix multiplication involve the multiplication of a row vector and a column vector. Specifically, in the expression R = AB,
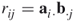
where 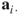 is the
is the 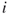 th row vector in matrix A and
th row vector in matrix A and 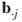 is the
is the 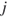 th column vector in matrix B. Thus, if
th column vector in matrix B. Thus, if
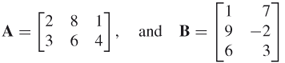
then
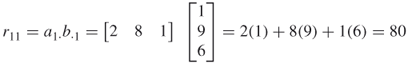
and
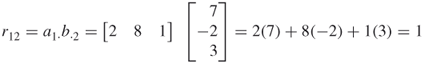
and
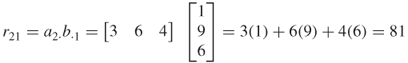
and
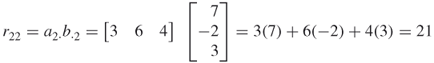
Hence,
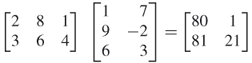
For matrix multiplication to be legal, the first matrix must have as many rows as the second matrix has columns. This, of course, is the requirement for multiplying a row vector by a column vector. The resulting matrix will have as many rows as the first matrix and as many columns as the second matrix. Because A has two rows and three columns, whereas B has three rows and two columns, the matrix multiplication may legally proceed and the resulting matrix will have two rows and two columns.
Because of these requirements, matrix multiplication is usually not commutative. That is, usually AB 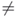 BA. And even if AB is a legal operation, there is no guarantee that BA will also be legal. For these reasons, the terms premultiply and postmultiply are often encountered in matrix algebra, whereas they are seldom encountered in scalar algebra.
BA. And even if AB is a legal operation, there is no guarantee that BA will also be legal. For these reasons, the terms premultiply and postmultiply are often encountered in matrix algebra, whereas they are seldom encountered in scalar algebra.
One special case to be aware of is when a column vector is postmultiplied by a row vector. Consider
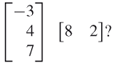
In this case, one simply follows the rules given above for the multiplication of two matrices. Note that the first matrix has one column and the second matrix has one row, so the matrix multiplication is legal. The resulting matrix will have as many rows as the first matrix (three) and as many columns as the second matrix (two). Hence, the result is
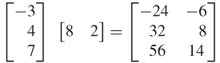
The transpose of a matrix is denoted by a prime (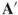 ) or a superscript t or T (
) or a superscript t or T (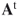 or
or 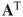 ). The first row of a matrix becomes the first column of the transpose matrix, the second row of the matrix becomes the second column of the transpose, etc. Thus,
). The first row of a matrix becomes the first column of the transpose matrix, the second row of the matrix becomes the second column of the transpose, etc. Thus,
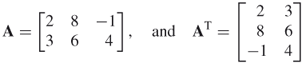
The transpose of a row vector will be a column vector, and the transpose of a column vector will be a row vector. The transpose of a symmetric matrix is simply the original matrix.
In scalar algebra, the inverse of a number is that number, which, when multiplied by the original number, gives a product of 1. Hence, the inverse of 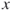 is simple
is simple  or, in slightly different notation,
or, in slightly different notation, 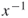 . In matrix algebra, the inverse of a matrix is that matrix, which, when multiplied by the original matrix, gives an identity matrix. The inverse of a matrix is denoted by the superscript
. In matrix algebra, the inverse of a matrix is that matrix, which, when multiplied by the original matrix, gives an identity matrix. The inverse of a matrix is denoted by the superscript 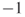 . Hence,
. Hence,
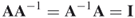
A matrix must be square to have an inverse, but not all square matrices have an inverse. In some cases, the inverse does not exist.
1. |
2.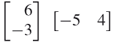 |
3. |
4.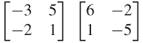 |
5.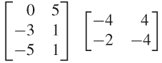 |
6.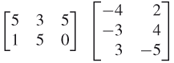 |
7.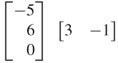 |
8.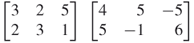 |
9.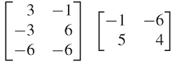 |
10.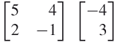 |
11.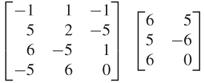 |
12.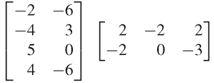 |
13.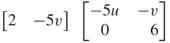 |
14.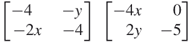 |
| Critical Thinking Question 1 Write an example of a matrix multiplication that is undefined. | Critical Thinking Question 2 In the expression 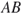 , if , if  is a is a 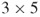 matrix, then what could be the dimensions of matrix, then what could be the dimensions of 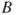 ? ? |