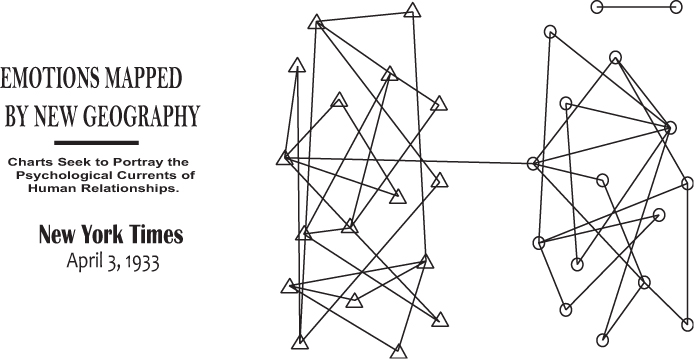
Figure 1.1 Emotions mapped by new geography.
The analysis of networks is not a recent trend. With historical examples dating back several centuries, its use in scientific enquiry has increased over the past few decades in particular. The term network can refer to any number of different types of networks, for example, social networks of people or a network of roads or a computer network. The Oxford dictionary defines a network as a group or system of interconnected people or things, suggesting that a network contains objects or people, and connections or links between these. By studying the objects, the links, and also the structure and dynamics of the network we can discover many important aspects that were previously not known. In this text, we focus on social network analysis. Linton Freeman describes the discipline.
“The social network approach is grounded in the intuitive notion that the patterning of social ties in which actors are embedded has important consequences for those actors. Network analysts, then, seek to uncover various kinds of patterns. And they try to determine the conditions under which those patterns arise and to discover their consequences” (Freeman, 2004).
People do not act in a manner independent from the context of their social interactions and environment. Moreover, there are patterns and behaviors of interaction that are common among people, if one can properly understand the social context in which they occur. This is not restricted to social ties between people. It may include knowledge, resources, tasks, beliefs, roles, organizations, and more, as well as peoples' interactions with these other factors. To better understand what social network analysis is, we provide Freeman's definition of four features that make up social network analysis:
“Beyond commitment to these four features, however, modern social network analysts also recognize that a wide range of empirical phenomena can be explored in terms of their structural patterning” (Freeman, 2004).
This structural perspective in the social sciences dates back to the establishment of the field. Comte (Martineau, 1895) identified two branches of sociology, statics, and dynamics. He further defined statics as the study of the “laws of social interconnection.” This is essentially the theoretical roots of social network analysis. The appeal of the network approach to problems has also appealed to others in a broad range of disciplines from physics to the other social sciences. As such, there are methods and tools that can be exchanged and applied to a wide variety of problems in many different fields. This has greatly enriched the development of the science and the contributions social network analysis has made to many different fields. Others in the early development of social science introduced data, methods, and theory, which we now recognize as social network analysis. Simmel (1909) defined society as existing “where a number of individuals enter into interaction.” The focus of the research of Simmel and his students was on the structure of social patterns.
Hobson, a famous economist at the turn of the twentieth century, presented an affiliation matrix on overlapping directorships of financiers in South Africa. There were five companies and six individuals. This was an early attempt at relational algebra, which we present in Chapter 7. This represents an important step forward in the ability to recognize and construct social network data. It also highlights how non-people nodes can impact our representation of a social network.
We find it interesting that the first evidence of social network data was derived from relational data rather than direct observation, which was not apparent in the literature until the 1920s. Systematic observation of social network data was introduced by Wellman (1926) who recorded data of preschool children during play. Blatz and Bott (1928) identified different forms of interaction among children. This enabled her to focus her observations on interaction specific to a research context.
The idea of different types of interaction, or different types of links, was the beginning of the formation of the underlying theory of meta-networks, proposed by Kathleen Carley years later. Meta-networks are discussed in Chapter 7. Recently, people have begun to refer to a subset of meta-networks as multilevel networks. In addition, Bott would focus on one child at a time to observe the different types of interaction with others. She recorded these data in matrices. Hagman compared the data collection approaches of observation and interview to reveal differences and bias in findings (Hagman, 1933). This became an important issue in social network analysis, studied extensively by Bernard and Killworth in a series of excellent papers on the topic. This issue is discussed in Chapter 8.
Most people credit the beginnings of social network analysis to Jacob Moreno with the graphical social network of interactions between school children in the New York Times (Moreno, 1932, 1934) displayed in Figure 1.1. Moreno initially referred to his research as “psychological geography,” but later changed the name to sociometry and started a journal of the same name in 1938.Moreno's work was largely theoretical and his social networks were more illustrative than mathematical representations. Recognizing this, Moreno teamed up with one of the earliest mathematical sociologists from Columbia University, Paul Lazarsfeld. Lazarsfeld developed a probabilistic model of a social network, which appeared in the first volume of Moreno's journal.
Figure 1.1 Emotions mapped by new geography.
Other groups began to explore social network analysis and structural approaches to social behavior. Lewin was a well-known sociologist who embraced the structural approach. He developed the Research Center for Group Dynamics at MIT with four of his former students including Cartwright and Festinger. Following Lewin's sudden death and MIT's decision to close the research center, the Center moved to the University of Michigan in 1948. Cartwright and Festinger recruited Frank Harary, who had earned his Ph.D. and was teaching in the Department of Mathematics, as a mathematical collaborator. Cartwright and Harary proposed a mathematical statement of the notion of cognitive balance proposed by Heider, which we discuss in Chapter 4. Others working in this research center conducted work on personal influence and the diffusion of rumors. In the 1950s, this group collected a famous multiyear data set on affinity in a university dormitory (Newcomb, 1961).
The Columbia University also made several important contributions to social network analysis. Robert Merton was a sociologist with a background in theory who teamed up with Paul Lazarsfeld, who was a mathematician working as a methodologist. They worked together throughout their careers, mainly in the areas of communication and what developed into market research. They also produced many Ph.D. students who became very influential in the field. Menzel and Katz (1956) investigated the diffusion of drug information among physicians, shaping our understanding of marketing. Peter Blau (1977) proposed homophily, which states that people with similar characteristics are more likely to meet. We present homophily in Chapter 4. Charles Kadushin developed the concept of social circles, which paved the way for subgroup analysis, which we discuss in Chapter 5.
Everett Rogers is another important figure in social network analysis during this time. His dissertation from Iowa State University involved some simple social network analysis methods in the study of the diffusion of innovations. He later introduced the concepts of early adopters and the bell curve and S-curves for the adoption of innovations. He extended his research to preventative health and other applications. As of the writing of this book, Rogers' book on “The Diffusion of Innovations” is the second most cited book in the social sciences. Noah Friedkin and Kathleen Carley extended Rogers' work to the diffusion of ideology, which is important for understanding radicalization. These concepts are presented in Chapter 6. Rogers also produced Ph.D. scholars who have made impressive contributions to the field, such as George Barnett, James Danowski, Peter Monge, Nan Lin, William Richards, and Thomas Valente.
In the 1960s, Davis and Leinhardt became interested in Cartwright and Harary's mathematical treatment of Heider's balance theory. Davis and Leinhardt introduced several formal mathematical models of relations between three actors, known as the triad. Their models dealt with transitivity, which is where actors develop relationships through their shared connection to others. Their work is presented in Chapter 4.
Independently, around the same time frame, mathematicians Paul Erd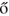
s andAlfréd Rényi made revolutionary discoveries in the evolution of “random graphs.” For our purposes, a graph is synonymous with a network. Erd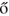s and Rényi use the term graph to refer to the field of mathematics called graph theory. This term was introduced by a chemist, Sylvester, in 1878, as mathematicians were applying their ideas to chemistry. In their eight papers, Erd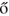s and Rényi evaluate the properties of random graphs with n nodes and l links. For a random graph, G, containing no links, at each time step a randomly chosen link among the possible links is added to G. All of the possible links are equiprobable. A general model used to generate random graphs is as follows: “For a given p, 
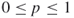, each potential link of G is chosen with probability p, independent of other links. Such a random graph is denoted by G(n,p), where each link is determined by flipping a coin, which has probability p of coming up heads.” In this model of random graphs, each link has an equal probability of occurring or not occurring within the graph. This random graph model also assumes that all nodes in the graph are present at the beginning and the number of nodes in the network is fixed and remains the same throughout the network's life. In addition, all nodes in this model are considered equal and are undistinguishable from each other.
Building upon Cartwright and Harary's work, and utilizing Erd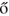s' theory of random graphs as well as the class of uniform distributions associated with these graphs, Holland and Leinhardt (1981) developed a variety of statistical tests for the analysis of social networks. Using a uniform distribution, these tests spread the total probability mass equally over all possible outcomes, thereby giving an equal probability to the existence of a link between any two nodes in the network. These statistical tests were used to develop a reference frame or constant benchmark to which observed data could be compared in order to determine how “structured a particular network was, or how far the network deviated from the benchmark” (Wasserman and Faust, 1994). While this text does not address the statistical treatment of networks, it is important for interested readers to be aware that there are well-developed statistical tests for networks.
One of the most important figures in social network analysis was Harrison White. Harrison was a physicist who became interested in social behavior. He was working at Carnegie Tech, where he met Nobel laureate Herbert Simon. Herbert Simon was a founding father of many scientific fields to include artificial intelligence, organization theory, complex systems, and computer simulation. He was also the first to propose preferential attachment as a mechanism to explain power law distributions in the 1950s. Simon's influence on Harrison White led him to pursue a second Ph.D. in Sociology from Princeton. Harrison then moved to Harvard, where he produced some of the most important leaders in the field of social network analysis including Peter Bearman, Paul Bernard, Phillip Bonacich, Scott Boorman, Ronald Breiger, Kathleen Carley, Mark Granovetter, Joel Levine, and Barry Wellman.He introduced blockmodeling to understand subgroups and interactions between them, which we explore in Chapter 5. He proposed the concept of structural equivalence. These concepts are foundational to understanding network structure. Linton Freeman states, “Contemporary network analysis could never have emerged without Harrison White's contributions” (Freeman, 2004).
Linton Freeman is another prolific scholar in the field of social network analysis. He defined the network centrality measures that form the core metrics of social networks. These measures provide mathematical expressions of informal power, diffusion reach, and direct influence in a network. These concepts represent the foundation of modern social network analysis and are presented in Chapters 2 and 3. Freeman also produced many Ph.D.s who have made numerous important contributions to the field, including Stephen P. Borgatti, Katherine Faust, Sue C. Freeman, Jeffery Johnson, David Krackhardt, and Lee Sailer.
Equally important to the development of social network analysis was the growth of a community of scholars interested in the field. Their collaboration was facilitated greatly by H. Russell Bernard and Alvin Wolfe with their organization of the Sunbelt conferences. Initially, Russ received a grant while he was teaching at the West Virginia University to host a small meeting of mathematicians, sociologists, and anthropologists working in the area of social network analysis in 1974. Several follow-on meetings occurred. By 1980, Russ had moved to the University of Florida and developed a friendship with Alvin Wolfe at the University of South Florida who was also interested in social network analysis. They decided that Florida was a nice place and that people would want to visit, especially to discuss networks. So they organized the first Sunbelt Conferences in Tampa, Florida, in February of 1981 and 1982. They established three rules. There would be no sessions during peak tanning hours. The older guys would sponsor a hospitality social for the younger guys to facilitate interaction in an informal setting. The conferences would be held in a warm, enjoyable place during the winter to attract people to attend. The Sunbelt conferences have grown in size significantly over the years and they now hold sessions throughout the day in multiple parallel tracks; however, it remains one of the most collaborative and accessible conferences in academia, bringing scholars across many disciplines together to collaborate on social network analysis. Later, Barry Wellman formed the academic professional society known as the “International Network of Social Network Analysts” (INSNA), which now organizes Sunbelt as its official annual meeting as well as editing the journal Connections. The final major development in social network analysis was the development of computer software to enable the mathematical calculations of network structure. Linton Freeman teamed up with Martin Everett and Steve Borgatti to produce UCI Net, which is one of the most widely used social network analysis software programs. Pajek is a European software tool that is well suited for displaying large data sets. Kathleen Carley developed the Organizational Risk Analyzer (ORA), which is designed to analyze meta-networks with multiple types of nodes and links, as well as a variety of visualization and overtime analysis features. The practical labs in this text are demonstrated in ORA. Recently, an open-source statistics package, R, featured powerful network analysis tools to include exponential random graph modeling with the statnet package and actor-oriented modeling with the Rsiena package. There are of course many other social network analysis tools. Social network analysis software has certainly enhanced the capability and practical application of the field.
Social network analysis offers more than pictures. It provides an entirely new dimension of analysis for organizational behavior. Traditional analysis focuses on individual attributes. Social networks focus on relationships between individuals. Traditional analysis assumes statistical independence, where social network analysis focuses on dependent observations. Traditional analysis seeks to identify the correlation between significant factors and a response variable. Social network analysis seeks to identify organizational structure. The underlying mathematics behind traditional analysis is calculus, the language of change. The corresponding mathematics behind social network analysis is linear algebra and graph theory. These differences can be significant in terms of how someone looks at social dynamics. We hope you are empowered by this treatment of an exciting and powerful approach to social science.
Blatz, W. E. and Bott, H. M. (1928). Parents and the Pre-School Child. J. M. Dent.
Blau, P. M. (1977). Inequality and Heterogeneity: A Primitive Theory of Social Structure. Free Press.
Freeman, L. (2004). The Development of Social Network Analysis: A Study in the Sociology of Science. Empirical Press.
Hagman, E. (1933). The Companionships of Preschool Children, by Elizabeth Pleger Hagman,… [Foreword by George D. Stoddard.]. University.
Holland, P. and Leinhardt, S. (1981). An exponential family of probability distributions for directed graphs. Journal of the American Statistical Association, 76(373):33–50.
Martineau, H. (1895). La Philosophie positive d'Auguste Comte. Luis Bahl.
Moreno, J. L. (1932). Application of the Group Method to Classification. National Committee on Prisons and Prison Labor.
Moreno, J. L. (1934). Who Shall Survive? Nervous and Mental Disease Publishing Company.
Newcomb, T. M. (1961). The Acquaintance Process. Holt, Rinehart and Winston.
Simmel, G. (1909). The problem of sociology. The American Journal of Sociology, 15(3):289–320.
Wasserman, S. and Faust, K. (1994). Social Network Analysis: Methods and Applications. Cambridge University Press.
Wellman, B. (1926). The Development of Motor Co-ordination in Young Children, an Experimental Study in the Control of Hand and Arm Movements, by Beth Wellman,… the University.