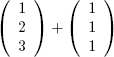Suppose we have a function f() that we wish to apply to all elements of a vector x. In many cases, we can accomplish this by simply calling f() on x itself. This can really simplify our code and, moreover, give us a dramatic performance increase of hundredsfold or more.
One of the most effective ways to achieve speed in R code is to use operations that are vectorized, meaning that a function applied to a vector is actually applied individually to each element.
You saw examples of vectorized functions earlier in the chapter, with the + and * operators. Another example is >.
> u <- c(5,2,8) > v <- c(1,3,9) > u > v [1] TRUE FALSE FALSE
Here, the > function was applied to u[1] and v[1], resulting in TRUE, then to u[2] and v[2], resulting in FALSE, and so on.
A key point is that if an R function uses vectorized operations, it, too, is vectorized, thus enabling a potential speedup. Here is an example:
> w <- function(x) return(x+1) > w(u) [1] 6 3 9
Here, w() uses +, which is vectorized, so w() is vectorized as well. As you can see, there is an unlimited number of vectorized functions, as complex ones are built up from simpler ones.
Note that even the transcendental functions—square roots, logs, trig functions, and so on—are vectorized.
> sqrt(1:9) [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751 2.828427 [9] 3.000000
This applies to many other built-in R functions. For instance, let’s apply the function for rounding to the nearest integer to an example vector y:
> y <- c(1.2,3.9,0.4) > z <- round(y) > z [1] 1 4 0
The point is that the round() function is applied individually to each element in the vector y. And remember that scalars are really single-element vectors, so the “ordinary” use of round() on just one number is merely a special case.
> round(1.2) [1] 1
Here, we used the built-in function round(), but you can do the same thing with functions that you write yourself.
As mentioned earlier, even operators such as + are really functions. For example, consider this code:
> y <- c(12,5,13) > y+4 [1] 16 9 17
The reason element-wise addition of 4 works here is that the + is actually a function! Here it is explicitly:
> '+'(y,4) [1] 16 9 17
Note, too, that recycling played a key role here, with the 4 recycled into (4,4,4).
Since we know that R has no scalars, let’s consider vectorized functions that appear to have scalar arguments.
> f function(x,c) return((x+c)^2) > f(1:3,0) [1] 1 4 9 > f(1:3,1) [1] 4 9 16
In our definition of f() here, we clearly intend c to be a scalar, but, of course, it is actually a vector of length 1. Even if we use a single number for c in our call to f(), it will be extended through recycling to a vector for our computation of x+c within f(). So in our call f(1:3,1) in the example, the quantity x+c becomes as follows:
This brings up a question of code safety. There is nothing in f() that keeps us from using an explicit vector for c, such as in this example:
> f(1:3,1:3) [1] 4 16 36
You should work through the computation to confirm that (4,16,36) is indeed the expected output.
If you really want to restrict c to scalars, you should insert some kind of check, say this one:
> f
function(x,c) {
if (length(c) != 1) stop("vector c not allowed")
return((x+c)^2)
}The vectorized functions we’ve been working with so far have scalar return values. Calling sqrt() on a number gives us a number. If we apply this function to an eight-element vector, we get eight numbers, thus another eight-element vector, as output.
But what if our function itself is vector-valued, as z12() is here:
z12 <- function(z) return(c(z,z^2))
Applying z12() to 5, say, gives us the two-element vector (5,25). If we apply this function to an eight-element vector, it produces 16 numbers:
x <- 1:8 > z12(x) [1] 1 2 3 4 5 6 7 8 1 4 9 16 25 36 49 64
It might be more natural to have these arranged as an 8-by-2 matrix, which we can do with the matrix function:
> matrix(z12(x),ncol=2)
[,1] [,2]
[1,] 1 1
[2,] 2 4
[3,] 3 9
[4,] 4 16
[5,] 5 25
[6,] 6 36
[7,] 7 49
[8,] 8 64But we can streamline things using sapply() (or simplify apply). The call sapply(x,f) applies the function f() to each element of x and then converts the result to a matrix. Here is an example:
> z12 <- function(z) return(c(z,z^2))
> sapply(1:8,z12)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 2 3 4 5 6 7 8
[2,] 1 4 9 16 25 36 49 64We do get a 2-by-8 matrix, not an 8-by-2 one, but it’s just as useful this way. We’ll discuss sapply() further in Chapter 4.