
In this chapter, we study a special class of linear operators, called compact operators.
Why should we study compact operators? One important reason is that they can be approximated by finite rank operators. So they play an important role in the numerical approximation of solutions to operator equations. We had seen that if H is an infinite-dimensional Hilbert space and A ∈ CL(H) with ||A|| < 1, then given y ∈ H, there is a unique x ∈ H such that

which is given by the Neumann series

But all of the operators A, A2, A3, ··· act on the infinite-dimensional H, so that computing these powers may not at all be feasible, and the convergence of the series may be “slow” (see Exercise 2.23, page 87). But now imagine that we can approximate A by finite matrices An and consider instead

where the yn → y as n → ∞, and the unknown xn are obtained by solving the finite linear algebraic equation (I – An)xn = yn. Then we can easily compute xn = (I – An)−1yn, and if xn → x, then we are able to determine x approximately. This wishful thinking can be made a reality if A is “compact”, as we shall see later on in this chapter when we learn Theorem 5.6 (page 218) on Galerkin approximations.
We begin by giving the definition of a compact operator.
Definition 5.1. (Compact operators). Let X, Y be normed spaces. A linear transformation T : X → Y is said to be compact if
for every bounded sequence (xn)n∈N contained in X, (Txn)n∈N has a convergent subsequence.
We will denote the set of all compact operators from X to Y by K(X, Y).
Why do we call such operators compact? The following result answers this question. Recall firstly that a closed and bounded set in an infinite dimensional normed space may fail to be compact (Example 1.26, page 48, and Example 1.28, page 50). So if T ∈ CL(X, Y), and B is the closed unit ball in X with centre 0, then although we know that T(B) is closed and bounded, it needn’t be compact. However, compact operators T are special in the sense that T(B) is guaranteed to be compact!
Theorem 5.1.
Let X, Y be normed spaces, and T : X → Y be a linear transformation. Then the following are equivalent:
(1)T is compact.
(2)The closure T(B) of the image under T of the closed unit ball, B := {x ∈ X : ||x||  1}, is compact.
1}, is compact.
Proof.
(1)  (2): Let (zn)n∈N be a sequence in T(B). Then there is a sequence (yn)n∈N in T(B) such that
(2): Let (zn)n∈N be a sequence in T(B). Then there is a sequence (yn)n∈N in T(B) such that

Let yn = Txn, xn ∈ B, n ∈ N. Since for all n we have ||xn||  1, and because T is compact, (yn)n∈N has a convergent subsequence, say (ynk)k∈N, converging to, say y. As each yn ∈ T(B), we have y ∈ T(B). From (5.1), (znk)k∈N converges to y too. Hence T(B) is compact.
1, and because T is compact, (yn)n∈N has a convergent subsequence, say (ynk)k∈N, converging to, say y. As each yn ∈ T(B), we have y ∈ T(B). From (5.1), (znk)k∈N converges to y too. Hence T(B) is compact.
(2)  (1): Let (xn)n∈N be a bounded sequence in X, and let M > 0 be such that for all n ∈ N, ||xn||
(1): Let (xn)n∈N be a bounded sequence in X, and let M > 0 be such that for all n ∈ N, ||xn||  M. Then (xn/M)n∈N is in B, and (T(xn)/M)n∈N is in T(B) ⊂ T(B). As T(B) is compact, (T(xn)/M)n∈N has a convergent subsequence. Thus (Txn)n∈N has a convergent subsequence. Consequently, T is compact.
M. Then (xn/M)n∈N is in B, and (T(xn)/M)n∈N is in T(B) ⊂ T(B). As T(B) is compact, (T(xn)/M)n∈N has a convergent subsequence. Thus (Txn)n∈N has a convergent subsequence. Consequently, T is compact.

Corollary 5.1.
Every compact operator is continuous, that is K(X, Y) ⊂ CL(X, Y).
Proof. Let B := {x ∈ X : ||x||  1}. If T is compact, then T(B) is compact, and in particular, bounded. So T(B) ⊂ T(B) is bounded too. So there is some M > 0 such that ||Tz||
1}. If T is compact, then T(B) is compact, and in particular, bounded. So T(B) ⊂ T(B) is bounded too. So there is some M > 0 such that ||Tz||  M for all z ∈ B. But this gives ||Tx||
M for all z ∈ B. But this gives ||Tx||  M ||x|| for all x ∈ X. (This is trivially true when x = 0, and if x ≠ 0, then by taking z = x/||x|| ∈ B, we have ||Tz||
M ||x|| for all x ∈ X. (This is trivially true when x = 0, and if x ≠ 0, then by taking z = x/||x|| ∈ B, we have ||Tz||  M, yielding the desired inequality.) So T ∈ CL(X, Y).
M, yielding the desired inequality.) So T ∈ CL(X, Y).

Is it true that K(X, Y) = CL(X, Y)? No:
Example 5.1. (Not all continuous linear transformations are compact). Let X be any infinite dimensional inner product space, for example ℓ2. We will show that the identity operator I ∈ CL(X) is not compact.
Let {u1, u2, u3, ···} be any orthonormal set in X. (Start with any countably infinite independent set, and use Gram-Schmidt.) Then ||un|| = 1 for all n ∈ N, and so the sequence (un)n∈N is bounded. However, the sequence (Iun)n∈N has no convergent subsequence, since for all n, m ∈ N with n ≠ m, we have ||Iun – Ium||2 = ||un – um||2 = 1 + 0 + 0 + 1 = 2, and this can’t be made as small as we please. Hence I is not compact, but is continuous.

In contrast to the above, it turns out that all finite rank operators are compact. Recall that an operator T is called a finite rank operator if its range, ran(T), is a finite-dimensional vector space. For ease of exposition, we will just prove this when Y is an inner product space.
Theorem 5.2. Let X be a normed space and Y be an inner product space. Suppose that T ∈ CL(X, Y) is such that ran(T) is finite dimensional.
Then T is compact.
Proof. Let {u1, ···, um} be an orthonormal basis for ran(T). Let (xn)n∈N be a bounded sequence in X. Suppose that M > 0 is such that ||xn||  M for all n ∈ N. We want to show that (Txn)n∈N has a convergent subsequence. (We will show that
M for all n ∈ N. We want to show that (Txn)n∈N has a convergent subsequence. (We will show that

for some subsequence (xnk)k∈N.) For all n ∈ N and each ℓ ∈ {1, . . . , m},
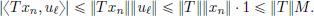
(xn)n∈N has some subsequence (xn(1))n∈N such that 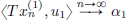 .
.
(xn(1))n∈N has some subsequence (xn(2))n∈N such that  .
.
(xn(m–1))n∈N has some subsequence (xn(m))n∈N such that  .
.
Claim: (Txn(m))n∈N converges to α1u1 + ··· αmum.

it follows that (Txn(m))n∈N is a convergent subsequence of the sequence (Txn)n∈N. Consequently T is compact.

In elementary linear algebra, not only were all linear transformations from Cn to Cm continuous, they were even compact!
Example 5.2. (L(Cn, Cm) = CL(Cn, Cm) = K(Cn, Cm)).
If A ∈ Cn×m, then TA ∈ CL(Cn, Cm) given by TAx = Ax, x ∈ Cn, is finite-rank because ran TA ⊂ Cm, and so TA is compact. In particular, the identity map I : Cd → Cd is compact.

We had seen that K(X, Y) ⊂ CL(X, Y). But CL(X, Y) is a vector space, with the usual pointwise operations. So it is natural to ask if K(X, Y) is a subspace of CL(X, Y). The answer is “yes”, and this is what we show next.
Theorem 5.3. 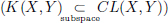 .
.
If X, Y are normed spaces, then K(X, Y) is a subspace of CL(X, Y).
Proof.
(S1)0 is compact since (0xn)n∈N = (0)n∈N is convergent for all bounded sequences (xn)n∈N in X.
(S2)If T, S are compact, and (xn)n∈N is bounded, then (Tn)n∈N has some subsequence (Txnk)k∈N that is convergent, and (Sxnk)k∈N has some subsequence (Sxnkℓ)ℓ∈N that is convergent. So ((T + S)xnkℓ)ℓ∈N is convergent. Thus T + S is compact.
(S3)If T, S are compact, α ∈ K and (xn)n∈N is bounded, then (Tn)n∈N has some subsequence (Txnk)k∈N that is convergent, and so it follows that  is convergent. Thus αT is compact.
is convergent. Thus αT is compact.

Since CL(X, Y) is a normed space, we can even ask if K(X, Y) is a closed subspace of CL(X, Y). We now show that if Y is a Banach space, then K(X, Y) is a closed subspace of CL(X, Y), or briefly:
“Limits of compact operators are compact.”
Theorem 5.4. Let X be a normed space, Y a Banach space, and (Tn)n∈N be a sequence in K(X, Y) that converges in CL(X, Y) to T ∈ CL(X, Y). Then T is compact.
Proof. Suppose that (xn)n∈N is a bounded sequence in X, and let M > 0 be such that for all n ∈ N, ||xn||  M. Since T1 is compact, (T1xn)n∈N has a convergent subsequence (T1xn(1))n∈N, say. Again, since (xn(1))n∈N is a bounded sequence, and T2 is compact, (T2xn(1))n∈N has a convergent subse-quence, say (T2xn(2))n∈N. We continue in this manner to obtain the following:
M. Since T1 is compact, (T1xn)n∈N has a convergent subsequence (T1xn(1))n∈N, say. Again, since (xn(1))n∈N is a bounded sequence, and T2 is compact, (T2xn(1))n∈N has a convergent subse-quence, say (T2xn(2))n∈N. We continue in this manner to obtain the following:

Consider the diagonal sequence x1, x2(1), x3(2), ··· .
By meditating on the above picture, one can convince oneself that
 , ··· is a subsequence of
, ··· is a subsequence of 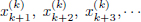 .
.
As  , ··· converges, its subsequence,
, ··· converges, its subsequence,

converges too, and so ( converges.
converges.

Hence 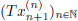 is a Cauchy sequence in Y and since Y is complete, it converges in Y. So, starting from the bounded sequence (xn)n∈N in X, we have found a subsequence
is a Cauchy sequence in Y and since Y is complete, it converges in Y. So, starting from the bounded sequence (xn)n∈N in X, we have found a subsequence 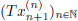 of the sequence (Txn)n∈N, that converges in Y. Consequently, T is compact.
of the sequence (Txn)n∈N, that converges in Y. Consequently, T is compact.

Corollary 5.2. Let X be a normed space, Y a Hilbert space, and (Tn)n∈N be a sequence of finite rank operators in CL(X, Y) that converges in CL(X, Y) to T ∈ CL(X, Y). Then T is compact.
Example 5.3. (When is a diagonal operator on ℓ2 compact?)
Let X = Y = ℓ2, (λn)n∈N be a bounded in K, and Λ ∈ CL(ℓ2) be “given by”

Then we had seen in Exercise 2.17 (page 76) that ||Λ|| =  |λn|.
|λn|.
Claim: Λ is compact if and only if 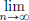 λn = 0.
λn = 0.
(If part): Consider for n ∈ N, the operators Λn ∈ CL(ℓ2) given by

Each Λn is a finite rank operator because ran Λn ⊂ span{e1, ··· , en}, where ek is the sequence with kth term equal to 1, and all others equal to 0. Hence Λn is compact. Then
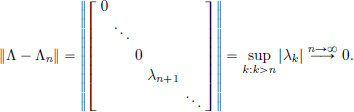
Consequently, Λ, being the uniform limit of a sequence of compact operators, is compact.
(Only if part): Suppose that Λ is compact, but it is not the case that
(λn)n∈N is convergent with limit 0, that is,

that is,

Taking N = 1, there exists n1 > 1 such that |λn1| 
 .
.
Taking N = n1, there exists n2 > n1 such that |λn2| 
 .
.
· · ·
Proceeding in this manner, we can construct inductively a subsequence (λnk)k∈N of (λn)n∈N such that for all k ∈ N, |λnk| 
 . Now consider the bounded sequence (enk)k∈N in ℓ2. We have (Λenk)n∈N = (λnk enk)k∈N. But for all
. Now consider the bounded sequence (enk)k∈N in ℓ2. We have (Λenk)n∈N = (λnk enk)k∈N. But for all  . This shows that (λnk enk)k∈N has no convergent subsequence, contradicting the compactness of Λ.
. This shows that (λnk enk)k∈N has no convergent subsequence, contradicting the compactness of Λ.

Exercise 5.1. (Hilbert Schmidt operators are compact.)
Let H be a Hilbert space with an orthonormal basis (u1, u2, u3, ···}.
Let T ∈ CL(H) be Hilbert-Schmidt, that is,  .
.
(1)If m ∈ N, then define Tm : H → H by Tmx =  .
.
Prove that Tm ∈ CL(H) and that  .
.
Hint: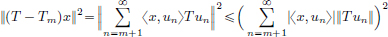 . and use the Cauchy-Schwarz inequality in ℓ2.
. and use the Cauchy-Schwarz inequality in ℓ2.
(2)Show that every Hilbert-Schmidt operator T is compact.
Hint:Using (1), conclude that T is the limit in CL(H) of the sequence of finite rank operators Tm, m ∈ N.
Exercise 5.2. Let H be a Hilbert space, and x0, y0 ∈ H be fixed.
Define x0  y0 : H → H by (x0
y0 : H → H by (x0  y0)(x) = 〈x, y0〉x0, x ∈ H.
y0)(x) = 〈x, y0〉x0, x ∈ H.
(1)Show that x0  y0 ∈ CL(H) and that ||x0
y0 ∈ CL(H) and that ||x0  y0||
y0||  ||x0||||y0||.
||x0||||y0||.
(2)Is x0  y0 compact?
y0 compact?
(3)Let A, B ∈ CL(H). Show that A(x0  y0)B = (Ax0)
y0)B = (Ax0)  (B*y0).
(B*y0).
Recall that CL(H) has the structure of a complex algebra with multiplication of T, S ∈ CL(H) taken as composition T  S ∈ CL(H). What is the relation of K(H q as a subset of CL(H) with respect to this operation of multiplication? The answer is that K(H) forms an “ideal” in CL(H).
S ∈ CL(H). What is the relation of K(H q as a subset of CL(H) with respect to this operation of multiplication? The answer is that K(H) forms an “ideal” in CL(H).
Definition 5.2. (Ideal in an algebra).
An ideal I of an algebra R is a subset I of R having the properties:
(I1) 0 ∈ I.
(I2) If a, b ∈ I, then a + b ∈ I.
(I3) If a ∈ I and r ∈ R, then ar ∈ I and ra ∈ I.
For example, if R = Z, the set of all integers, then I = 2Z, the set of all even integers, is an ideal in R. In algebra, ideals are important, since they serve as kernels of algebra homomorphisms.
Theorem 5.5. Let H be a Hilbert space. Then we have:
(1)If T ∈ K(H) is compact and S ∈ CL(H), then TS is compact.
(2)If T ∈ CL(H) is compact, then T* is compact.
(3)If T ∈ CL(H) is compact and S ∈ K(H), then ST is compact.
Proof.
(1)Let (xn)n∈N be a bounded sequence in H. Suppose M > 0 is such that ||xn||  M for all n ∈ N. Since S ∈ CL(H), it follows that (Sxn)n∈N is also a bounded sequence (||Sxn||
M for all n ∈ N. Since S ∈ CL(H), it follows that (Sxn)n∈N is also a bounded sequence (||Sxn||  ||S||||xn||
||S||||xn||  ||S||M). As T is compact, (T(Sxn))n∈N = (TSxn)n∈N has a convergent subsequence. Thus TS is compact.
||S||M). As T is compact, (T(Sxn))n∈N = (TSxn)n∈N has a convergent subsequence. Thus TS is compact.
(2)As T ∈ K(H) and T* ∈ CL(H), by part (1) above, TT* is compact.
Let (xn)n∈N be a bounded sequence in X and ||xn||  M for all n.
M for all n.
Then (TT*xn)n∈N has some convergent subsequence, say (TT*xnk)k∈N. Hence, given an  > 0,
> 0,
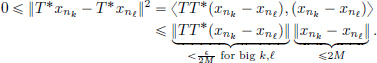
So (T*xnk)k∈N is a Cauchy sequence, and as H is a Hilbert space, it is convergent. Consequently, T* is compact.
(3)Since T is compact, by part (2), it follows that T* is also compact.
Moreover, as S* ∈ CL(H), we have T*S* is compact, using part (1). From part (2) again, we get (T* S*)* = S**T** = ST is compact.

Summary: The set K(H) is a closed ideal of CL(H).
Example 5.4. (Compact operators on infinite dimensional Hilbert spaces are never invertible.) Let H be an infinite dimensional Hilbert space, and T ∈ K(H). If T were invertible in CL(H), then T−1 ∈ CL(H), so that I = TT−1 ∈ K(H), which is false, since we had seen that the identity operator on an infinite dimensional Hilbert space is not compact.

Exercise 5.3. Let T ∈ CL(H), where H is an infinite-dimensional Hilbert space.
(1)Give an example of H and T such that T2 is compact, but T isn’t.
(2)Show that if T is self-adjoint and T2 is compact, then T is compact.
Exercise 5.4. Determine if the following statements are true for all S, T ∈ CL(H), where H is an infinite dimensional Hilbert space.
(1)If S and T are compact, then S + T is compact.
(2)If S + T is compact, then S or T is compact.
(3)If S or T is compact, then ST is compact.
(4)If ST is compact, then S is compact or T is compact.
Exercise 5.5. Let H be a Hilbert space. Let A ∈ CL(H) be fixed.
We define Λ ∈ CL(CL(H)) by Λ(T) = A*T + TA, T ∈ CL(H).
Show that the subspace K(H) of CL(H) is Λ-invariant, that is, ΛK(H) ⊂ K(H).
Compact operators play an important role in numerical analysis since they can be approximated by finite rank operators. This means that when we want to solve an operator equation involving a compact operator, then we can replace the compact operator by a sufficiently good finite-rank approximation, reducing the operator equation to an equation involving finite matrices. The solution can then be found using linear algebra. In this section we will prove Theorems 5.6 and 5.7, which form the basis of the Galerkin Method in numerical analysis.
Consider the equation (I – K)x = y, where K is a given operator on a Hilbert space H, y ∈ H is a given vector, and x ∈ H is the unknown. Suppose we consider instead the equation (I – K0)x0 = y0, where K0 is close to K, and y0 is close to y. The following result describes how big ||x – x0|| can get.

Theorem 5.6.
Let
(1)H be a Hilbert space,
(2)K ∈ CL(H) be such that I – K is invertible in CL(H),
(3)K0 ∈ CL(H) be such that  := ||(K – K0)(I – K)−1|| < 1.
:= ||(K – K0)(I – K)−1|| < 1.
Then for every y, y0 ∈ H, there exist unique x, x0 ∈ X such that
(a) (I – K)x = y,
(b) (I – K0)x0 = y0, and
(c)  .
.
Note that from part (c) we see that the upper estimate on ||x – x0|| is small when y ≈ y0 and K ≈ K0. So the result is telling us that if we have a scheme of approximating the operator K and the vector y, then we can solve the equation
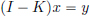
approximately by solving instead the equation
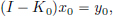
and moreover, we have a handle on how large the error ||x – x0|| can get. Later on, in Theorem 5.7 we will see that for compact operators K, such an approximating scheme for producing K0 does exist.
Proof. As ||(K – K0) (I – K)−1|| < 1, by the Neumann Series Theorem, we have I + (K – K0)(I – K)−1 is invertible, and so

is invertible as well. Moreover,


and so

Let y, y0 ∈ X. Since I – K and I – K0 are invertible, there are unique x, x0 ∈ X such that (I – K)x = y and (I – K0)x0 = y0. Also,
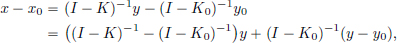
and so 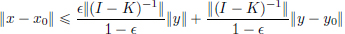 , as desired.
, as desired.

Question: If K is compact, y ∈ H, then how do we find approximations K0 to K and y0 to y?
Answer: Via projections.
Theorem 5.7. (Galerkin approximation).
Let
(1)H be a Hilbert space,
(2)K be a compact operator on H,
(3)(Pn)n∈N be a sequence of projections (P2n = P*n = ∈ CL(H)) of finite rank such that Pn converges strongly to I (for all x ∈ H,  Pnx = x).
Pnx = x).
Then PnKPn 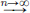 K in CL(H).
K in CL(H).
We remark that a mere strong convergence assumption results in uniform convergence, and this miracle happens since we have a compact operator at hand. We also remark that a standard way of producing such a sequence of projections is via choosing an orthonormal basis {u1, u2, u3, ···} for H, and then we can take Pn to be the projection onto the closed finite dimensional subspace Y = span{u1, ···, un}:

Proof. We’ll prove the following claims:
(1)PnK 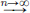 K in CL(H) (projection approximation),
K in CL(H) (projection approximation),
(2)KPn 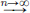 K in CL(H) (Sloan approximation),
K in CL(H) (Sloan approximation),
(3)PnKPn 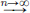 K in CL(H) (Galerkin approximation).
K in CL(H) (Galerkin approximation).
(1): For all x ∈ H, we have
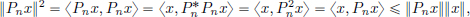
and so ||Pnx||  ||x|| for all x, that is, ||Pn||
||x|| for all x, that is, ||Pn||  1. Suppose that it is not the case that PnK – K converges to 0 in CL(H) as n → ∞. This means that
1. Suppose that it is not the case that PnK – K converges to 0 in CL(H) as n → ∞. This means that

Thus there exists an  > 0 such that for all N ∈ N, there exists an n > N, such that ||PnK – K|| >
> 0 such that for all N ∈ N, there exists an n > N, such that ||PnK – K|| >  .
.
Hence there exists an  > 0 such that for all N ∈ N, there exists an n > N, such that sup{||(PnK – K)x|| : x ∈ H, ||x||
> 0 such that for all N ∈ N, there exists an n > N, such that sup{||(PnK – K)x|| : x ∈ H, ||x||  1} >
1} >  .
.
So there exists an  > 0 such that for all N ∈ N, there exists an n > N, such that there exists an x ∈ H with ||x||
> 0 such that for all N ∈ N, there exists an n > N, such that there exists an x ∈ H with ||x||  1, but ||(PnK – K)x|| >
1, but ||(PnK – K)x|| >  .
.
The last statement allows us to construct a sequence (xnk)k∈N in X such that ||xnk|| 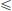 1 and ||(PnkK – K)xnk|| >
1 and ||(PnkK – K)xnk|| >  as follows.
as follows.
Taking N = 1, there exists an n1 > 1 and an xn1 ∈ H with ||xn1||  1 but ||(Pn1K – K)xn1|| >
1 but ||(Pn1K – K)xn1|| >  .
.
Taking N = n1, there exists an n2 > n1 and an xn2 ∈ H with ||xn2||  1 but ||(Pn2K – K)xn2|| >
1 but ||(Pn2K – K)xn2|| >  .
.
Taking N = n3, there exists an n3 > n2 and an xn3 ∈ H with ||xn3||  1 but ||(Pn3K – K)xn3|| >
1 but ||(Pn3K – K)xn3|| >  .
.
Thus (xnk)k∈N is bounded and ||(PnkK – K)xnk|| >  for all ks.
for all ks.
As (xnk)k∈N is bounded and K is compact, there exists a subsequence, say (Kxnkℓ)ℓ∈N, of (Knk)k∈N, that is convergent to y, say. Then we have
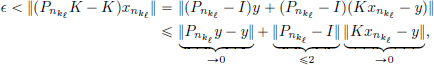
a contradiction. This completes the proof of (1).
(2): As K is compact, so is K*. Thus by (1),  in CL(H). But
in CL(H). But  , and so KPn
, and so KPn 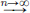 K in CL(H).
K in CL(H).

This completes the proof

So, in Theorem 5.6, what is y0, K0? We can take K0 = PnKPn, where Pn is the orthogonal projection onto span{u1, ···, un}, and y0 = Pny. We note that ||y0 – y|| = ||Pny – y|| is small for large n, and ||K – PnKPn|| is small for large n. Thus  = ||(K – K0)(I – K)−1|| is small. So if we look at the equation (I – PnKPn)x0 = Pny instead of (I – K)x = y, then ||x – x0|| can be made as small as we please by taking n large enough. We give a simple toy example.
= ||(K – K0)(I – K)−1|| is small. So if we look at the equation (I – PnKPn)x0 = Pny instead of (I – K)x = y, then ||x – x0|| can be made as small as we please by taking n large enough. We give a simple toy example.
Example 5.5.
Consider the operator  on ℓ2. For all x = (xn)n∈N ∈ ℓ2,
on ℓ2. For all x = (xn)n∈N ∈ ℓ2,

So ||K|| 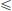
 , and I – K is invertible in CL(ℓ2).
, and I – K is invertible in CL(ℓ2).
K is Hilbert-Schmidt as  . So K is compact.
. So K is compact.
Let  . To find approximate solutions of the equation
. To find approximate solutions of the equation

we fix an n ∈ N, and solve instead x – PnKPnx = Pny, that is, the system

The approximate solutions for n = 1, 2, 3, 4, 5 are given (correct up to four decimal places) by

while the exact unique solution to the equation (I – K)x = y is given by

To 4 decimal places, this is x = (0.5, 0.3333, 0.2500, 0.2000, 0.1667, ···).

In elementary linear algebra, one learns about the Spectral Theorem, which says that every Hermitian matrix T ∈ Cd×d is diagonalisable, with a basis of orthonormal eigenvectors u1, ··· , ud ∈ Cd, and corresponding real eigenvalues λ1 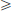 ···
··· 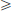 λd, so that
λd, so that
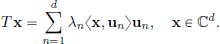
Towards seeking a generalisation to the Hilbert space case, we’ll now show that while the spectrum of a general self-adjoint operator may be quite complicated, for a compact self-adjoint operator, things are quite similar to the finite-dimensional case.
Theorem 5.8. (Spectral Theorem for compact, self-adjoint operators).
Let H be a Hilbert space and T = T* ∈ K(H) have infinite rank.
Then there exist orthonormal eigenvectors un, n ∈ N, with corresponding eigenvalues λn, n ∈ N, such that  λn = 0, and for all x ∈ H,
λn = 0, and for all x ∈ H,
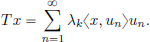
We had already seen that the eigenvalues of a self-adjoint operator must be real, and that the eigenvectors corresponding to distinct eigenvalues are orthogonal. It is also clear that for any eigenvalue λ of T, we have that |λ|  ||T||, since if v ∈ H\{0} is a corresponding eigenvector, then
||T||, since if v ∈ H\{0} is a corresponding eigenvector, then
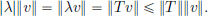
Let us make a few more observations which will be used in proving the spectral theorem.
Lemma 5.1. If T = T* ∈ CL(H), then ||T|| =  .
.
Proof. Let M :=  .
.
If x ∈ H is such that ||x|| = 1, then we have by Cauchy-Schwarz that  . Thus M
. Thus M  ||T||.
||T||.
It remains to show the reverse inequality. For any x, y ∈ H,

and so  . We note that by the definition of M,
. We note that by the definition of M,
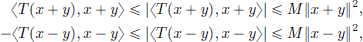
and so from the above, together with the Parallelogram Law, we obtain

Let θ ∈ R be such that 〈T x, y〉 = |〈T x, y〉|eiθ. Replacing y by eiθy yields

If Tx = 0 or x = 0, then ||Tx|| 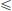 M ||x|| is trivially true.
M ||x|| is trivially true.
If Tx ≠ 0 and x ≠ 0, then with  in the above, we obtain
in the above, we obtain
||Tx||||x|| 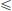 M ||x||2 and so ||Tx||
M ||x||2 and so ||Tx|| 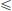 M ||x||. Thus ||T||
M ||x||. Thus ||T|| 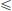 M.
M.

Moreover if T is compact, then this bound M is achieved, thanks to the following result. Indeed, if x is the unit-norm eigenvector corresponding to the eigenvalue λ whose modulus |λ| = ||T||, then

Lemma 5.2. If H is a nontrivial Hilbert space and T = T* ∈ K(H), then either ||T|| or −||T|| is an eigenvalue of T.
Proof. If T = 0, then this is trivial. So let us suppose that T is nonzero. From the previous lemma, it follows that there is a sequence (x′n)n∈N of unit norm vectors in H such that 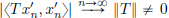 . But as 〈Tx′n, x′n〉 is real, we have 〈Tx′n, x′n〉 is either |〈Tx′n, x′n〉| or −|〈Tx′n, x′n〉|. Thus either for infinitely many n, 〈Tx′n, x′n〉 is positive (and then the subsequence (〈Txn, xn〉)n∈N with these ns converges to ||T||), or for infinitely many n, 〈Tx′n, x′n〉 is negative (and then the subsequence (〈Txn, xn〉)n∈N with these ns converges to −||T||). So 〈Txn, xn〉
. But as 〈Tx′n, x′n〉 is real, we have 〈Tx′n, x′n〉 is either |〈Tx′n, x′n〉| or −|〈Tx′n, x′n〉|. Thus either for infinitely many n, 〈Tx′n, x′n〉 is positive (and then the subsequence (〈Txn, xn〉)n∈N with these ns converges to ||T||), or for infinitely many n, 〈Tx′n, x′n〉 is negative (and then the subsequence (〈Txn, xn〉)n∈N with these ns converges to −||T||). So 〈Txn, xn〉 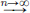 λ, where λ is either ||T|| or −||T||. We have
λ, where λ is either ||T|| or −||T||. We have

So Txn – λxn 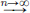 0. As T is compact, there is a subsequence, say (Txnk)k∈N of (Txn)n∈N that converges, say, to y ∈ H. Then (xnk)k∈N converges to y/λ, because λxnk = Txnk – (Txnk – λxnk)
0. As T is compact, there is a subsequence, say (Txnk)k∈N of (Txn)n∈N that converges, say, to y ∈ H. Then (xnk)k∈N converges to y/λ, because λxnk = Txnk – (Txnk – λxnk) 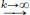 y – 0 = y.
y – 0 = y.
Thanks to the continuity of T, we obtain
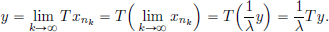
Hence Ty = λy, and y ≠ 0 since 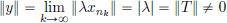 .
.

Lemma 5.3. Let H be a Hilbert space, T = T* ∈ CL(H), and Y be a T-invariant closed subspace of H. Then:
(1)Y⊥ is also T-invariant.
(2)The restriction T|Y⊥ : Y⊥ → Y⊥ of T to the Hilbert space Y⊥ is also self-adjoint.
(3)If T is in addition compact, then T|Y⊥ is also compact.
Proof.
(1)Let z ∈ Y⊥. For all y ∈ Y, we have that Ty ∈ Y (Y is T-invariant!), and so 〈Tz, y〉 = 〈z, T*y〉 = 〈z, Ty〉 = 0. Thus Tz ∈ Y⊥.
(2)Y⊥, being a closed subspace of a Hilbert space, is itself a Hilbert space. As Y⊥ is T-invariant, the restriction T|Y⊥ : Y⊥ → Y⊥ is well-defined. Let us denote this restriction by  . For z1, z2 ∈ Y⊥,
. For z1, z2 ∈ Y⊥,
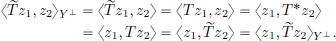
Thus T|Y⊥ is self-adjoint.
(3)Finally, suppose that T is compact. Let (zn)n∈N be a bounded sequence in Y⊥. Then ||zn||Y⊥ = ||zn||. So (zn)n∈N is a bounded sequence in H. As T is compact, (Tzn)n∈N = ( zn)n∈N has a subsequence (
zn)n∈N has a subsequence ( xnk)k∈N that is convergent in H. In particular, (
xnk)k∈N that is convergent in H. In particular, ( xnk)k∈N is Cauchy in H, and hence also Cauchy in Y⊥ (because ||
xnk)k∈N is Cauchy in H, and hence also Cauchy in Y⊥ (because || zn –
zn –  zm|| = ||
zm|| = || zn –
zn –  zm||Y⊥). As Y⊥ is complete, it follows that (
zm||Y⊥). As Y⊥ is complete, it follows that ( xnk)k∈N is convergent in Y⊥. So T|Y⊥ is compact.
xnk)k∈N is convergent in Y⊥. So T|Y⊥ is compact.

Proof. (Of the spectral theorem). Let H1 := H and T1 := T.
By Lemma 5.2, there exists an eigenvalue λ1 of T1 and a corresponding eigenvector u1 such that ||u1|| = 1 and |λ1| = ||T1||.
Set H2 = (span{u1})⊥. Then H2 is a closed subspace of H1, and it is also T-invariant: TH2 ⊂ H2. Let T2 := T|H2. Then T2 is self-adjoint and compact. There exist an eigenvalue λ2 of T2 and a corresponding eigenvector u2 such that ||u2|| = 1 and |λ2| = ||T2||. So

Clearly, {u1, u2} are orthonormal, Tu1 = λ1u1 and Tu2 = λ2u2.
Now let H3 := (span{u1, u2})⊥. Then H3 is a closed subspace of H, H3 ⊂ H2, and as span{u1, u2} is T-invariant, we obtain TH3 ⊂ H3. Let T3 := T|H3. Then T3 is self-adjoint and compact. Thus there exist an eigenvalue λ3 of T3 and a corresponding eigenvector u3 ∈ H3, such that ||u3|| = 1 and |λ3| = ||T3||. As u3 ∈ H3 ⊂ H2, we have that

Continuing in this manner, we get a sequence λ1, λ2, λ3, ··· of eigenvalues of T, and a corresponding set of eigenvectors u1, u2, u3, ··· , such that

The process would stop at some n if Hn := (span{u1, ···, un−1})⊥ would become {0}, but we will now show that thanks to the infinite rank assumption on T, this case is impossible. Suppose, on the contrary, that Hn = {0}.
For any x ∈ H, we have 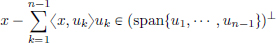 .
.
As Hn = {0}, we obtain  .
.
So ran T is spanned by Tu1, ··· , Tun, a contradiction to the assumption that T has infinite rank. Thus one has an infinite sequence of eigenvectors u1, u2, u3, ··· with eigenvalues λ1, λ2, λ3, ··· .
Let us now show that (|λn|)n∈N converges to 0. As it is decreasing, it converges to  . If
. If  > 0, then for n ≠ m,
> 0, then for n ≠ m,

But this contradicts the fact that T is compact, since the sequence (Tun)n∈N should have some convergent (and hence Cauchy) subsequence. So (|λn|)n∈N converges to 0, and hence (λn)n∈N also converges to 0.
For all x ∈ H, we have 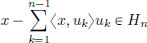 , and so
, and so
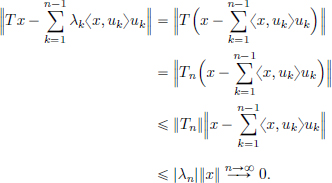
The last inequality above follows from Bessel’s Inequality (Exercise 4.15, page 172). Hence  for all x ∈ H.
for all x ∈ H.

Exercise 5.6.
Let H be an infinite dimensional Hilbert space, and T = T* ∈ K(H) be one-to-one. Show that the eigenvectors of T form an orthonormal basis for H.
Exercise 5.7. Let H be a Hilbert space. Suppose that T = T* ∈ K(H) has infinite rank, and is positive, that is, 〈T x, x〉 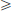 0 for all x ∈ H.
0 for all x ∈ H.
Prove that T has a square root, that is, an operator  ∈ CL(H) such that (
∈ CL(H) such that ( )2 = T.
)2 = T.