 .
.Solution to Exercise 0.1, page ix
We have  .
.
On the other hand, 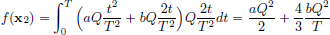 .
.
Clearly f(x2) > f(x1), and so the mining operation x1 is preferred to x2 because it incurs a lower cost.
Solutions to the exercises from Chapter 1
Solution to Exercise 1.1, page 7
True. Indeed we have:
(V1)For all x, y, z > 0, x  (y
(y  z) = x
z) = x  (yz) = x(yz) = (xy)z = (xy)
(yz) = x(yz) = (xy)z = (xy)  z = (x
z = (x  y)
y)  z.
z.
(V2)For all x > 0, x  1 = x1 = x = 1x = 1
1 = x1 = x = 1x = 1  x.
x.
(So 1 serves as the zero vector in this vector space!)
(V3)If x > 0, then 1/x > 0 too, and x  (1/x) = x(1/x) = 1 = (1/x)x = (1/x)
(1/x) = x(1/x) = 1 = (1/x)x = (1/x)  x.
x.
(Thus 1/x acts as the inverse of x with respect to the operation  .)
.)
(V4)For all x, y > 0, x  y = xy = yx = y
y = xy = yx = y  x.
x.
(V5)For all x > 0, 1 · x = x1 = x.
(V6)For all x > 0 and all  .
.
(V7)For all x > 0 and all  .
.
(V8)For all x, y > 0,  .
.
We remark that V is isomorphic to the one dimensional vector space R (with the usual operations): indeed, it can be checked that the maps log : V → R and exp : R → V are linear transformations, and are inverses of each other.
Solution to Exercise 1.2, page 7
We prove this by contradiction. Suppose that C[0, 1] has dimension d. Consider functions xn(t) = tn, t ∈ [0, 1], n = 1, ··· , d. Since polynomials are continuous, we have xn ∈ C[0, 1] for all n = 1, ··· , d.
First we prove that xn, n = 1, ··· , d, are linearly independent in C[0, 1]. Suppose not. Then there exist αn ∈ R, n = 1, ··· , d, not all zeros, such that α1 · x1 + ··· + αd · xd = 0. Let m ∈ {1, ··· , d} be the smallest index such that αm ≠ 0. Then for all t ∈ [0, 1], αmtm + ··· + αdtd = 0. In particular, for all t ∈ [0, 1], we have 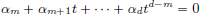 .
.
Thus for all n ∈ N we have 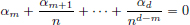 .
.
Passing the limit as n → 8, we obtain αm = 0, a contradiction. So the functions xn, n = 1, ··· , d, are linearly independent in C[0, 1].
Next, we get the contradiction to C[0, 1] having dimension d. Since any independent set of cardinality d in a d-dimensional vector space is a basis for this vector space, {xn : n = 1, ··· , d} is a basis for C[0, 1]. Since the constant function 1 (taking value 1 everywhere on [0, 1]) belongs to C[0, 1], there exist βn ∈ R, n = 1, ··· , d, such that 1 = β1 · x1 + ··· + βd · xd. In particular, putting t = 0, we obtain the contradiction that 1 = 0: 1 = 1(0) = (β1 · x1 + ··· + βd · xd)(0) = 0.
Solution to Exercise 1.3, page 7
(“If ” part.) Suppose that ya = yb = 0. Then we have:
(S1)If x1, x2 ∈ S, then x1 + x2 ∈ S. As x1, x2 ∈ C1[a, b], also x1 + x2 ∈ C1[a, b]. Moreover, x1(a) + x2(a) = 0 + 0 = 0 = ya and x1(b) + x2(b) = 0 + 0 = 0 = yb.
(S2)If x ∈ S and α ∈ R, then α · x ∈ S. Indeed, as x ∈ C1[a, b], and α ∈ R,
we have α·x ∈ C1[a, b], and (α·x)(a) = α0 = 0 = ya, (α·x)(b) = α0 = 0 = yb.
(S3)0 ∈ S, since 0 ∈ C1[a, b] and 0(a) = 0 = ya = yb = 0(b).
Hence, S is a subspace of a vector space C1[a, b]
(“Only if ” part.) Suppose that S is a subspace of C1[a, b]. Let x ∈ S.
Then 2 · x ∈ S. Therefore, (2 · x)(a) = ya, and so ya = (2 · x)(a) = 2x(a) = 2ya.
Thus ya = 0. Moreover, (2 · x)(b) = yb, and so yb = (2 · x)(b) = 2x(b) = 2yb.
Hence also yb = 0.
Solution to Exercise 1.4, page 10

Solution to Exercise 1.5, page 14
From the triangle inequality, we have that ||x|| = ||y + x − y||  ||y|| + ||x − y||, for all x, y ∈ X. So for all x, y ∈ X, ||x|| − ||y||
||y|| + ||x − y||, for all x, y ∈ X. So for all x, y ∈ X, ||x|| − ||y||  ||x − y||.
||x − y||.
Interchanging x, y, we get  .
.
So for all x, y ∈ X, − (||x|| − ||y||)  ||x − y||.
||x − y||.
Combining the results from the first two paragraphs, we obtain |||x|| − ||y|||  ||x − y|| for all x, y ∈ X.
||x − y|| for all x, y ∈ X.
Solution to Exercise 1.6, page 14
No, since for example (N2) fails if we take x = 1 and α = 2:
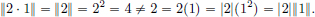
Solution to Exercise 1.7, page 15
We verify that (N1), (N2), (N3) are satisfied by || · ||Y:
(N1)For all y ∈ Y, ||y||Y = ||y||X  0.
0.
If y ∈ Y and ||y||Y = 0, then ||y||X = 0, and so y = 0 ∈ X.
But 0 ∈ Y, and so y = 0 ∈ Y.
(N2)If y ∈ Y and α ∈ R, then α · y ∈ Y and 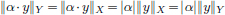 .
.
(N3)If y1, y2 ∈ Y, then y1 + y2 ∈ Y.
Also,  .
.
Solution to Exercise 1.8, page 15
(1) We first consider the case 1  p < ∞, and then p = ∞. Let 1
p < ∞, and then p = ∞. Let 1  p < ∞.
p < ∞.
(N1)If x = (x1, ··· , xd) ∈ Rd then  .
.
If x ∈ Rd and ||x||p = 0, then ||x||pp = 0. that is,  .
.
So |xn| = 0 for 1  n
n  d, that is, x = 0.
d, that is, x = 0.
(N2)Let x = (x1 , ··· , xd) ∈ Rd, and α ∈ R.
Then 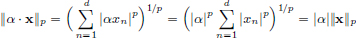 .
.
(N3)Let x = (x1, ··· , xd) ∈ Rd and y = (y1 , ··· , yd) ∈ Rd.
If p = 1, then we have |xn + yn|  |xn| + |yn| for 1
|xn| + |yn| for 1  n
n  d.
d.
By adding these, ||x + y||1  ||x||1 + ||y||1, establishing (N3) for p = 1.
||x||1 + ||y||1, establishing (N3) for p = 1.
Now consider the case 1 < p < ∞.
If x + y = 0, then ||x + y||p = ||0||p = 0  ||x||p + ||y||p trivially.
||x||p + ||y||p trivially.
So we assume that x + y ≠ 0. By Hölder’s Inequality, we have

where we used q(p − 1) = p in order to obtain the last equality.
Similarly, 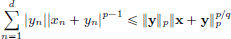 . Consequently,
. Consequently,

Dividing throughout by 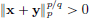 , we obtain
, we obtain  . This completes the proof that (Rd, || · ||p) is a normed space for 1
. This completes the proof that (Rd, || · ||p) is a normed space for 1  p < ∞.
p < ∞.
Now we consider the case p = ∞.
(N1)If x = (x1 , ··· , xd) ∈ Rd, then ||x||∞ = max{|x|, ··· , |xd|}  0.
0.
If x ∈ Rd and ||x||∞ = 0, then max{|x1|, ··· , |xd|} = 0, and so |xn| = 0 for 1  n
n  d, thart is, x = 0.
d, thart is, x = 0.
(N2)Let x = (x1 , ··· , xd) ∈ Rd, and α ∈ R.
Then  .
.
(N3)Let x = (x1, ··· , xd) ∈ Rd and y = (y1, ··· , yd) ∈ Rd.
We have  for 1
for 1  n
n  d.
d.
So it follows that ||x + y||∞  ||x||∞ + ||y||∞, establishing (N3) for p = ∞.
||x||∞ + ||y||∞, establishing (N3) for p = ∞.
(2) See the following pictures.
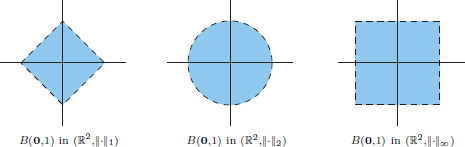
(3) We have for x = (a, b) ∈ R2 that

So  .
.
We have  . We have
. We have

giving 1/p  hp
hp  0 for all p, and so hp → 0 as p → ∞.) So it follows by the Sandwich Theorem1 that
0 for all p, and so hp → 0 as p → ∞.) So it follows by the Sandwich Theorem1 that  .
.
The balls Bp(0, 1) grow to B∞(0, 1) as p increases.
Solution to Exercise 1.9, page 16
(1)If x, y ∈ B(0, 1), then for all α ∈ (0, 1), (1 − α) · x + α · y ∈ B(0, 1) too, since


(3)B(0, 1) is not convex: taking x = (1, 0), y = (0, 1) and α = 1/2, we obtain  , and so
, and so  .
.
Solution to Exercise 1.10, page 16
We’ll verify that (N1), (N2), (N3) hold.
(N1)If x ∈ C[a, b], then |x(t)|  0 for all t ∈ [0, 1], and so
0 for all t ∈ [0, 1], and so  .
.
Let x ∈ C[a, b] be such that ||x||1 = 0. If x(t) = 0 for all t ∈ (a, b), then by the continuity of x on [a, b], it follows that x(t) = 0 for all t ∈ [a, b] too, and we are done! So suppose that it is not the case that for all t ∈ (a, b), x(t) = 0. Then there exists a t0 ∈ (a, b) such that x(t0) ≠ 0. As x is continuous at t0, there exists a δ > 0 small enough so that a < t0 − δ, t0 + δ < b, and such that for all t ∈ [a, b] such that t0 − δ < t < t0 + δ, |x(t) − x(t0)| < |x(t0)|/2. Then for t0 − δ < t < t0 + δ, we have, using the “reverse” Triangle Inequality from Exercise 1.5, page 14, that

So  .
.
This is a contradiction. Hence x = 0.
(N2)For x ∈ C[a, b], α ∈ R,  .
.
(N3)Let x, y ∈ C[a, b]. Then
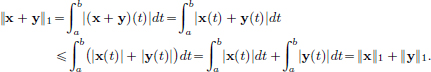
Solution to Exercise 1.11, page 17
(N1)For x ∈ Cn[a, b], clearly  .
.
If x ∈ Cn[a, b] is such that ||x||n,∞ = 0, then ||x||∞ + ··· + ||x(n)||∞ = 0, and since each term in this sum is nonnegative, we have ||x||∞ = 0, and so x = 0.
(N2)Let x ∈ Cn[a, b] and α ∈ R. Then
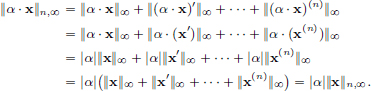
(N3)Let x, y ∈ Cn[a, b]. For all 0  k
k  n, ||x(k) + y(k)||∞
n, ||x(k) + y(k)||∞  ||x(k)||∞ + ||y(k)||∞, by the Triangle Inequality for || · ||∞ Consequently,
||x(k)||∞ + ||y(k)||∞, by the Triangle Inequality for || · ||∞ Consequently,

Solution to Exercise 1.12, page 17
(1)Let k1, k2, m1, m2, n1, n2 ∈ Z, p ł m1, m2, n1, n2 and  .
.
If k1 > k2, then pk1−k2m1n2 = m2n1, which implies that p | m2n1, and as p is prime, this would mean p | m1 or p | n1, a contradiction. Hence k1  k2. Similarly, we also obtain k2
k2. Similarly, we also obtain k2  k1.
k1.
Thus k1 = k2. Consequently,  , and so | · |p is well-defined.
, and so | · |p is well-defined.
(2)If 0 ≠ r ∈ Q, then we can express r as 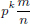 , with k, m, n ∈ Z, and p
, with k, m, n ∈ Z, and p  m, n.
m, n.
We see that  . If r = 0, then |r|p = |0|p = 0 by definition.
. If r = 0, then |r|p = |0|p = 0 by definition.
Thus |r|p  0 for all r ∈ R. Also if r ≠ 0, then |r|p > 0. Hence |r|p = 0 implies that r = 0.
0 for all r ∈ R. Also if r ≠ 0, then |r|p > 0. Hence |r|p = 0 implies that r = 0.
(3)The claim is obvious if r1 = 0 or r2 = 0. Suppose that r1 ≠ 0 and r2 ≠ 0.
Let 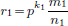 and
and  .
.
So  . As p
. As p  m1, p
m1, p  m2, and p is prime, we have p
m2, and p is prime, we have p  m1m2.
m1m2.
Similarly p  n1n2. Thus
n1n2. Thus  .
.
(4)The inequality is trivially true if r1 = 0 or r2 = 0 or if r1 + r2 = 0.
Assume r1 ≠ 0, r2 ≠ 0, and r1 + r2 ≠ 0.
Let  , with k1, k2, m1, m2, n1, n2 ∈ Z, p
, with k1, k2, m1, m2, n1, n2 ∈ Z, p  m1, m2, n1, n2. We have
m1, m2, n1, n2. We have
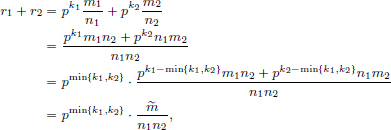
where  := pk1−min{k1,k2} m1n2 + pk2−min{k1,k2} n1m2 (≠ 0, since r1 + r2 ≠ 0). By the Fundamental Theorem of Arithmetic, there exists a unique integer
:= pk1−min{k1,k2} m1n2 + pk2−min{k1,k2} n1m2 (≠ 0, since r1 + r2 ≠ 0). By the Fundamental Theorem of Arithmetic, there exists a unique integer 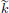
 0 and an integer m such that
0 and an integer m such that  and p
and p  m. Clearly p
m. Clearly p  n1n2.
n1n2.
Hence r1 + r2 =  , with p
, with p  m, n1n2.
m, n1n2.
So 

This yields the Triangle Inequality:
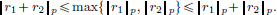
Solution to Exercise 1.13, page 17
(N1)Clearly  for all M = [mij] ∈ Rm×n.
for all M = [mij] ∈ Rm×n.
If ||M||∞ = 0, then |mij| = 0 for all 1  i
i  m, 1
m, 1  j
j  n, that is, M = [mij] = 0, the zero matrix.
n, that is, M = [mij] = 0, the zero matrix.
(N2)For M = [mij] ∈ Rm×n and α ∈ R, we have

(N3)For P = [pij], Q = [qij] ∈ Rm×n, |pij + qij|  |pij| + |qij|
|pij| + |qij|  ||P||∞ + ||Q||∞.
||P||∞ + ||Q||∞.
As this holds for all i, j, ||P + Q||∞ =  .
.
Solution to Exercise 1.14, page 19
Consider the open ball B(x, r) = {y ∈ X : ||x − y|| < r} in X. If y ∈ B(x, r), then ||x − y|| < r. Define r′ = r − ||x − y|| > 0. We claim that B(y, r′) ⊂ B(x, r). Let z ∈ B(y, r′). Then ||z − y|| < r′ = r − ||x − y|| and so ||x − z||  ||x − y|| + ||y − z|| < r. Hence z ∈ B(x, r). The following picture illustrates this.
||x − y|| + ||y − z|| < r. Hence z ∈ B(x, r). The following picture illustrates this.
Solution to Exercise 1.15, page 19
The point 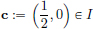 , but for each r > 0, the point
, but for each r > 0, the point 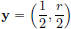 belongs to the ball B(c, r), but not to I, since ||y − c||2 =
belongs to the ball B(c, r), but not to I, since ||y − c||2 = 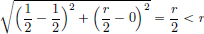 , but
, but  ≠ 0. See the following picture.
≠ 0. See the following picture.

Solution to Exercise 1.16, page 19
Using the following picture, it can be seen that the collections O1, O2, O∞ of open sets in the normed spaces (R2, || · ||1), (R2, || · ||2), (R2, || · ||∞), respectively, coincide.

Solution to Exercise 1.17, page 20
If Fi, i ∈ I, is a family of closed sets, then X\Fi, i ∈ I, is a family of open sets. Hence  is open. So
is open. So  is closed.
is closed.
If F1, ··· , Fn are closed, then X\F1, ··· , X\Fn are open, and so the intersection  of these finitely many open sets is open as well.
of these finitely many open sets is open as well.
Thus  is closed.
is closed.
For showing that the finiteness condition cannot be dropped, we’ll consider the normed space X = R, and simply rework Example 1.15, page 20, by taking complements.
We know that Fn := R\(−1/n, 1/n), n ∈ N, is closed and the union of these, 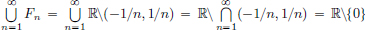 which is not closed, since if it were, its complement R\(R\{0}) = {0} would be open, which is false.
which is not closed, since if it were, its complement R\(R\{0}) = {0} would be open, which is false.
Solution to Exercise 1.18, page 20
Consider the closed ball B(x, r) = {y ∈ X : ||x − y||  r} in X. To show that B(x, r) is closed, we’ll show its complement, U := {y ∈ X : ||x − y|| > r}, is open. If y ∈ U, then ||x − y|| > r. Define r′ = ||x − y|| − r > 0. We claim that B(y, r′) ⊂ U. Let z ∈ B(y, r′). Then ||z − y|| < r′ = ||x − y|| − r and so ||x − z||
r} in X. To show that B(x, r) is closed, we’ll show its complement, U := {y ∈ X : ||x − y|| > r}, is open. If y ∈ U, then ||x − y|| > r. Define r′ = ||x − y|| − r > 0. We claim that B(y, r′) ⊂ U. Let z ∈ B(y, r′). Then ||z − y|| < r′ = ||x − y|| − r and so ||x − z||  ||x − y|| − ||y − z|| > ||x − y|| − (||x − y||− r) = r. Hence z ∈ U.
||x − y|| − ||y − z|| > ||x − y|| − (||x − y||− r) = r. Hence z ∈ U.
Solution to Exercise 1.19, page 20
(1)False.
For example, in the normed space R, consider the set [0, 1). Then [0, 1) is not open, since every open ball B with centre 0 contains at least one negative real number, and so B has points not belonging to [0, 1).
On the other hand, this set [0, 1) is not closed either, as its complement is C := (−∞, 0) ∪ [1, ∞), which is not open, since every open ball B′ with centre 1 contains at least one positive real number strictly less than one, and so B′; contains points that do not belong to C.
(2)False. R is open in R, and it is also closed.
(3)True. Ø and X are both open and closed in any normed space X.
(4)True. [0, 1) is neither open nor closed in R.
(5)False.
0 ∈ Q, but every open ball centred at 0 contains irrational numbers; just consider 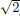 /n, with a sufficiently large n.
/n, with a sufficiently large n.
(6)False.
Consider the sequence (an)n∈N given by a1= , and for n > 1, an+1 =
, and for n > 1, an+1 = 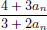 . Then it can be shown, using induction on n, that (an)n∈N is bounded below by
. Then it can be shown, using induction on n, that (an)n∈N is bounded below by 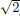 , and that (an)n∈N is monotone decreasing. (Example 1.19, page 31.) So (an)n∈N is convergent with a limit L satisfying
, and that (an)n∈N is monotone decreasing. (Example 1.19, page 31.) So (an)n∈N is convergent with a limit L satisfying  , and so L2 = 2.
, and so L2 = 2.
As L must be positive (the sequence is bounded below by  ), it follows that L =
), it follows that L =  . So every ball with centre
. So every ball with centre  and a positive radius contains elements from Q (terms an for large n), showing that R\Q is not open, and hence Q is not closed.
and a positive radius contains elements from Q (terms an for large n), showing that R\Q is not open, and hence Q is not closed.
(Alternately, let c ∈ R have the decimal expansion c = 0.101001000100001 ···. The number c is irrational because2 it has a nonterminating and nonrepeating decimal expansion. The sequence of rational numbers obtained by truncation, namely 0.1, 0.101, 0.101001, 0.1010010001, 0.101001000100001, ··· converges with limit c, and so every ball with centre c and a positive radius contains elements from Q, showing again that R \ Q is not open, and hence Q is not closed.)
(7)True.  As each (n, n + 1) is open, so is their union.
As each (n, n + 1) is open, so is their union.
Hence Z = R\(R\Z) is closed.
We have already seen in Exercise 1.14, page 19, that the interior of S, namely the open ball B(0, 1) = {x ∈ X : ||x|| < 1} is open. Also, it follows from Exercise 1.18, page 20, that the exterior of the closed ball B(0, 1), namely the set U = {x ∈ X : ||x|| > 1} is open as well. Thus, the complement of S, being the union of the two open sets B(0, 1) and U, is open. Consequently, S is closed.
If X = {0}, then {0} is clearly closed, since X\{0} = Ø is open.
Now suppose that X ≠ {0}, and let x ∈ X. We want to show that U := X\{x} is open. Let y ∈ U := X\{x}, and set r := ||x – y|| > 0. We claim that the open ball B(y, r) is contained in U. If z ∈ B(y, r), then ||y – z|| < r, and so ||z – x||  ||x – y|| – ||y – z||
||x – y|| – ||y – z||  r – ||y – z|| > r – r = 0. Hence z ≠ x, and so z ∈ X\{x} = U. Consequently U is open, and so {x} = X\U is closed.
r – ||y – z|| > r – r = 0. Hence z ≠ x, and so z ∈ X\{x} = U. Consequently U is open, and so {x} = X\U is closed.
If F is empty, then it is closed.
If F is not empty, then F = {x1, ··· , xn} =  {xi}, for some x1, ···, xn ∈ X.
{xi}, for some x1, ···, xn ∈ X.
As F is the finite union of the closed sets {x1}, ···, {xn}, F is closed too.
Let x, y ∈ R and x < y. By the Archimedean property of R, there is a positive integer n such that n > 1/(y – x), that is n(y – x) > 1. Also, there are positive integers m1, m2 such that m1 > nx and m2 > –nx, so that –m2 < nx < m1. Thus we have nx ∈ [–m2, –m2 + 1) ∪ [–m2 + 1, –m2 + 2)∪···∪[m1 – 1, m1). Hence there is an integer m such that m – 1  nx < m. We have nx < m
nx < m. We have nx < m  1 + nx < ny, and so dividing by n, we have x < q := m/n < y. Consequently, between any two real numbers, there is a rational number.
1 + nx < ny, and so dividing by n, we have x < q := m/n < y. Consequently, between any two real numbers, there is a rational number.
Let x ∈ R and let  > 0. Then there is a rational number y such that x –
> 0. Then there is a rational number y such that x –  < y < x +
< y < x +  , that is, |x – y| <
, that is, |x – y| <  . Hence Q is dense in R.
. Hence Q is dense in R.
Let x ∈ R and let  > 0. If x ∈ R\Q, then taking y = x, we have |x – y| = 0 <
> 0. If x ∈ R\Q, then taking y = x, we have |x – y| = 0 <  . If on the other hand, x ∈ Q, then let n ∈ N be such that n >
. If on the other hand, x ∈ Q, then let n ∈ N be such that n >  /
/ so that with y := x +
so that with y := x +  /n, we have y ∈ R\Q, and |x – y| =
/n, we have y ∈ R\Q, and |x – y| =  /n <
/n <  . So R\Q is dense in R.
. So R\Q is dense in R.
Let x = (xn)n∈N ∈ ℓ2, and  > 0. Let N ∈ N be such that
> 0. Let N ∈ N be such that 
Then y := (x1, ···, xN, 0, ···) ∈ c00, and 
Thus ||x – y||2 <  . Consequently, c00 is dense in ℓ2.
. Consequently, c00 is dense in ℓ2.
Consider the set D of all finitely supported sequences with rational terms. Then D is a countable set since it is a countable union of countable sets. We now show that D is dense in ℓ1. Let x := (xn)n∈N ∈ ℓ1 and let r > 0.
Let N ∈ N be large enough so that 
As Q is dense in R, there exist q1, ···, qN ∈ Q such that 
With x′ := (q1, ···, qN, 0, ···) ∈ D, 
By the Binomial Theorem, we have

Putting s = t, we get 1 = (t + (1 – t))n 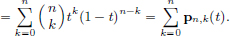
Keeping s fixed, and differentiating (7.1) with respect to t yields

Multiplying throughout by t gives
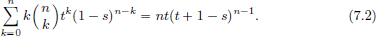
With 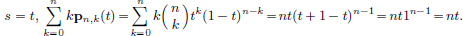
Differentiating (7.2) with respect to t yields
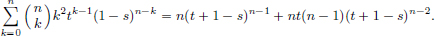
Multiplying throughout by t yields

Setting s = t now gives
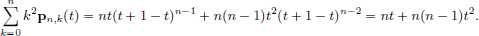
Hence
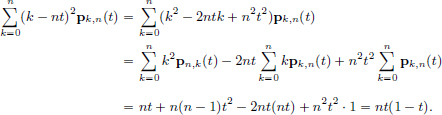
(1)We check that the relation ~ is reflexive, symmetric and transitive.
(ER1)(Reflexivity) If ||·|| is a norm on X, then for all x ∈ X, we have that 1 · ||x|| = ||x|| = 1 · ||x||, and so ||·|| ~ ||·||.
(ER2)(Symmetry) If ||·||a ~ ||·||b, then there exist positive m, M such that for all x ∈ X, m||x||b  ||x||a
||x||a  M ||x||b. A rearrangement of this gives (1/M)||x||a
M ||x||b. A rearrangement of this gives (1/M)||x||a  ||x||b
||x||b  (1/m)||x||a, x ∈ X, and so ||·||2 ~ ||·||1.
(1/m)||x||a, x ∈ X, and so ||·||2 ~ ||·||1.
(ER3)(Transitivity) If ||·||a ~ ||·||b and ||·||b ~ ||·||c, then there exist positive constants Mab, Mbc, mab, mbc such that for all x ∈ X, we have that mab||x||b  ||x||a
||x||a  Mab||x||b and mbc ||x||c
Mab||x||b and mbc ||x||c  ||x||b
||x||b  Mbc ||x||c.
Mbc ||x||c.
Thus mabmbc||x||c  mab||x||b
mab||x||b  ||x||a
||x||a  Mab||x||b
Mab||x||b  MabMbc ||x||c, and so ||·||a ~ ||·||c.
MabMbc ||x||c, and so ||·||a ~ ||·||c.
(2)Suppose that ||·||a ~ ||·||b. Because ~ is an equivalence relation, it is enough to just prove that if U is open in (X, ||·||b), then U is open in (X, ||·||a) too, and similarly, if (xn)n∈N is Cauchy (respectively) convergent in (X, ||·||b), then it is Cauchy (respectively convergent) in (X, ||·||a) as well. Let m, M > 0 be such that for all x ∈ X, m||x||b  ||x||a
||x||a  M||x||b.
M||x||b.
Let U be open in (X, ||·||b), and x ∈ U. Then as U is open in (X, ||·||b), there exists an r > 0 such that Bb(x, r) := {y ∈ X : ||y – x||b < r} ⊂ U. But if y ∈ X satisfies ||y – x||a < mr, then ||y – x||b  (1/m)||y – x||a < (1/m)mr = r, and so y ∈ Bb(x, r) ⊂ U. Hence Ba(x, mr) := {y ∈ X : ||y – x||a < mr} ⊂ U. So it follows that U is open in (X, ||·||a) too.
(1/m)||y – x||a < (1/m)mr = r, and so y ∈ Bb(x, r) ⊂ U. Hence Ba(x, mr) := {y ∈ X : ||y – x||a < mr} ⊂ U. So it follows that U is open in (X, ||·||a) too.
Now suppose that (xn)n∈N is a Cauchy sequence in (X, ||·||b). Let  > 0. Then there exists an N ∈ N such that for all n > N, ||xn – xm||b <
> 0. Then there exists an N ∈ N such that for all n > N, ||xn – xm||b <  /M. Hence for all n > N, ||xn – xm||a
/M. Hence for all n > N, ||xn – xm||a  M ||xn – xm||b < M · (
M ||xn – xm||b < M · ( /M) =
/M) =  .
.
Consequently, (xn)n∈N is a Cauchy sequence in (X, ||·||a) as well.
If (xn)n∈N is a convergent sequence in (X, ||·||b) with limit L, then for  > 0, there exists an N ∈ N such that for all n > N, ||xn – L||b <
> 0, there exists an N ∈ N such that for all n > N, ||xn – L||b <  /M. Thus for all n > N, ||xn – L||a
/M. Thus for all n > N, ||xn – L||a  M ||xn – L||b < M · (
M ||xn – L||b < M · ( /M) =
/M) =  . So (xn)n∈N is convergent with limit L in (X, ||·||a) too.
. So (xn)n∈N is convergent with limit L in (X, ||·||a) too.
(1)Let L > 0 be such that for all x, y ∈ R, |f(x) – f(y)| = 
Then in particular, with 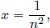 n ∈ N, and y = 0, we obtain
n ∈ N, and y = 0, we obtain 
Thus n  L for all n ∈ N, which is absurd. So f is not Lipschitz.
L for all n ∈ N, which is absurd. So f is not Lipschitz.
(2)x1(0) = 0 and x2(0) = 02/4 = 0, and so x1, x2 satisfy the initial condition.
For all t  0,
0, 
So x1, x2 are both solutions to the given Initial Value Problem.
Let F be closed, and (xn)n∈N be a sequence in F which converges to x. Suppose that x ∉ F. Since F is closed, there is an open ball B(x, r) := {x ∈ X : ||x – x|| < r} with r > 0, which is contained in X\F. But with  := r > 0, there exists an N ∈ N such that for all n > N, ||xn – x|| < r. In particular, ||xN+1 – x|| < r, so that F ∋ xN+1 ∈ B(x, r) ⊂ X\F, a contradiction. Hence x ∈ F.
:= r > 0, there exists an N ∈ N such that for all n > N, ||xn – x|| < r. In particular, ||xN+1 – x|| < r, so that F ∋ xN+1 ∈ B(x, r) ⊂ X\F, a contradiction. Hence x ∈ F.
Now suppose that for every sequence (xn)n∈N in F, convergent in X with a limit x ∈ X, we have that the limit x ∈ F. We want to show that X\F is open. Suppose it isn’t. Then3 ¬[∀x ∈ X\F, ∃r > 0 such that B(x, r) ⊂ X\F]. In other words, ∃x ∈ X\F such that ∀r > 0, B(x, r) ∩ F ≠ Ø. So with r = 1/n, n ∈ N, we can find an xn ∈ B(x, r) ∩ F. Then we obtain a sequence (xn)n∈N in F satisfying ||xn – x|| < 1/n for all n ∈ N. Thus (xn)n∈N converges to x. But x ∉ F, contradicting the hypothesis. Hence X\F is open, that is, F is closed.
Let (xn)n∈N in c00 be given by 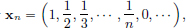 n ∈ N.
n ∈ N.
Then with 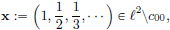 we have
we have
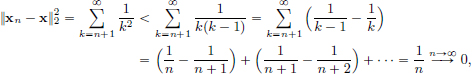
showing that c00 is not closed.
(1)Suppose that F is a closed set containing S. Let L be a limit point of S.
Then there exists a sequence (xn)n∈N in S\{L} which converges to L.
As each xn ∈ S\{L} ⊂ S ⊂ F, and since F is closed, it follows that L ∈ F.
So all the limit points of S belong to F. Hence S ⊂ F.
S is closed. Suppose that (xn)n∈N is a sequence in S that converges to L.
We would like to prove that L ∈ S. If L ∈ S, then L ∈ S, and we are done.
So suppose that L ∉ S. Now for each n, we define the new term x′n as follows:
1°If xn ∈ S, then x′n := xn.
2°If xn ∉ S, then xn must be a limit point of S, and so B(xn, 1/n) must contain some element, say x′n, of S.
Hence we have 
Thus (x′n)n∈N is a sequence in S\{L} which converges to L, and so L is a limit point of S, that is, L ∈ S. Consequently S is closed.
(2)We first note that if y ∈ Y, then there exists a (yn)n∈N in Y that converges to y. Indeed, this is obvious if y is a limit point of Y, and if y ∈ Y, then we may just take (yn)n∈N as the constant sequence with all terms equal to y. We have:
(S1)Let x, y ∈ Y. Let (xn)n∈N, (yn)n∈N be sequences in Y that converge to x, y, respectively. Then xn + yn ∈ Y ⊂ Y for each n ∈ N, and (xn + yn)n∈N converges to x + y. But as Y is closed, it follows that x + y ∈ Y too.
(S2)Let α ∈ K, y ∈ Y. Let (yn)n∈N be a sequence in Y that converges to y. Then α · yn ∈ Y ⊂ Y for each n ∈ N, and (α · yn)n∈N converges to α · y.
But as Y is closed, it follows that α · y ∈ Y too.
(S3)0 ∈ Y ⊂ Y.
Hence Y is a closed subspace.
(3)The proof is similar to part (2). Let x, y ∈ C. Then there exist sequences (xn)n∈N and (yn)n∈N in C that converge to x, y, respectively. If α ∈ (0, 1), then (1 – α)x + αy = (1 – α) 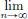 xn + α
xn + α 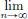 yn =
yn = 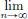 ((1 – α)xn + αyn).
((1 – α)xn + αyn).
As (1 – α)xn + αyn ∈ C ⊂ C for all n ∈ N, and since C is closed, it follows that (1 – α)x + αy ∈ C too.
(4)Suppose that D is dense in X. Let x ∈ X\D. If n ∈ N, then the ball B(x, 1/n) must contain an element dn ∈ D. The sequence (dn)n∈N converges to x because ||x – dn|| < 1/n, n ∈ N. Hence x is a limit point of D, that is, x ∈ D.
So X\D ⊂ D. Also D ⊂ D. Thus X = D ∪ (X\D) ⊂ D ⊂ X, and so X = D. Now suppose that X = D. If x ∈ X\D = D\D, then x is a limit point of D, and so there is a sequence (dn)n∈N in D that converges to x. Thus given an  > 0, there is an N such that ||x – dN|| <
> 0, there is an N such that ||x – dN|| <  , that is, dN ∈ D ∩ B(x,
, that is, dN ∈ D ∩ B(x,  ).
).
On the other hand, if x ∈ D, and  > 0, then x ∈ B(x,
> 0, then x ∈ B(x,  ) ∩ D.
) ∩ D.
Hence D is dense in X.
Let (xn)n∈N) ℓ1. Then  and so
and so 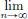 |xn| = 0.
|xn| = 0.
Thus there exists an N ∈ N such that |xn|  1 for all n
1 for all n  N. For all n
N. For all n  N, |xn|2 = |xn| · |xn|
N, |xn|2 = |xn| · |xn|  |xn| · 1 = |xn|. By the Comparison Test4,
|xn| · 1 = |xn|. By the Comparison Test4, 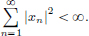
Hence (xn)n∈N ∈ ℓ2.
 while the Harmonic Series
while the Harmonic Series 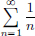 diverges.
diverges.
(ℓ1, ||·||2) is not a Banach space: Let us suppose, on the contrary, that it is a Banach space, and we will arrive at a contradiction by showing a Cauchy sequence which is not convergent in (ℓ1, ||·||2).
Consider for n ∈ N, 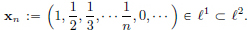 Then (xn)n∈N converges in ℓ2 to
Then (xn)n∈N converges in ℓ2 to  because
because 
So (xn)N is a Cauchy sequence in (ℓ2, ||·||2), and so it is also Cauchy in (ℓ1, ||·||2). As we have assumed that (ℓ1, ||·||2) is a Banach space, it follows that the Cauchy sequence (xn)n∈N must be convergent to some element x′ ∈ ℓ1 ⊂ ℓ2. But by the uniqueness of limits (when we consider (xn)n∈N as a sequence in ℓ2), we must have x = x′ ∈ ℓ1, which is false, since we know that the Harmonic Series diverges. This contradiction proves that (ℓ1, ||·||2) is not a Banach space.
Let (an)n∈N be a Cauchy sequence in c0. Then this is also a Cauchy sequence in ℓ∞, and hence convergent to a sequence in ℓ∞, say a. We’ll show that a ∈ c0. We write  and
and 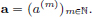 Let
Let  > 0. Then there exists an N ∈ N such that ||aN – a||∞ <
> 0. Then there exists an N ∈ N such that ||aN – a||∞ <  . In particular, for all m ∈ N,
. In particular, for all m ∈ N,  <
<  . But as aN ∈ c0, we can find an M such that for all m > M,
. But as aN ∈ c0, we can find an M such that for all m > M,  Consequently, for m > M, we have from the above that
Consequently, for m > M, we have from the above that  Thus a ∈ c0 too.
Thus a ∈ c0 too.
Given  > 0, let N ∈ N be large enough so that for all n > N, ||xn – x|| <
> 0, let N ∈ N be large enough so that for all n > N, ||xn – x|| <  . Then for all n > N, we have ||xn|| – ||x||
. Then for all n > N, we have ||xn|| – ||x||  ||xn – x|| <
||xn – x|| <  , and so it follows that the sequence (||xn||)n∈N is R is convergent, with limit ||x||.
, and so it follows that the sequence (||xn||)n∈N is R is convergent, with limit ||x||.
First consider the case 1  p < ∞.
p < ∞.
(N1)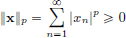 for all x = (x1, x2, x3, ···) ∈ ℓp.
for all x = (x1, x2, x3, ···) ∈ ℓp.
If  then |xn| = 0 for all n, and so x = 0.
then |xn| = 0 for all n, and so x = 0.
(N2)||α · x||p =  = |α| ||x||p, for x ∈ ℓp, α ∈ K.
= |α| ||x||p, for x ∈ ℓp, α ∈ K.
(N3)Let x = (x1, x2, ···) and y = (y1, y2, ···) belong to ℓp. Let d ∈ N.
By the Triangle Inequality for the ||·||p-norm on Rd,
Passing the limit as d tends to ∞ yields ||x + y||p  ||x||p + ||y||p.
||x||p + ||y||p.
Now consider the case p = ∞.
(N1)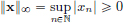 for all x = (x1, x2, x3, ···) ∈ ℓ∞.
for all x = (x1, x2, x3, ···) ∈ ℓ∞.
If  then |xn| = 0 for all n, that is, x = 0.
then |xn| = 0 for all n, that is, x = 0.
(N2)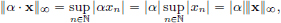 for x ∈ ℓ∞, α ∈ K.
for x ∈ ℓ∞, α ∈ K.
(N3)Let x = (x1, x2, ···) and y = (y1, y2, ···) belong to ℓ∞.
Then for all k, |xk + yk|  |xk| + |yk|
|xk| + |yk|  ||x||∞ + ||y||ℓ, and so
||x||∞ + ||y||ℓ, and so

From Exercise 1.11, page 17, taking n = 1, (C1[a, b], ||·||1,∞) is a normed space. We show that (C1[a, b], ||·||1,∞) is complete. Let (xn)n∈N be a Cauchy sequence in C1[a, b]. Then ||xn – xm||∞  ||xn – xm||∞ + ||x′n – x′m||1,∞, and so (xn)n∈N is a Cauchy sequence in (C[a, b], ||·||∞), and hence convergent to, say, x ∈ C[a, b]. Also, ||x′n – x′m||∞
||xn – xm||∞ + ||x′n – x′m||1,∞, and so (xn)n∈N is a Cauchy sequence in (C[a, b], ||·||∞), and hence convergent to, say, x ∈ C[a, b]. Also, ||x′n – x′m||∞  ||xn – xm||∞ + ||x′n – x′m||1,∞ = ||xn – xm||1,∞, shows that (x′n)n∈N is a Cauchy sequence in (C[a, b], ||·||∞), and hence convergent to say, y ∈ C[a, b]. We will now show that x ∈ C1[a, b], and x′ = y. Let t ∈ [a, b]. By the Fundamental Theorem of Calculus,
||xn – xm||∞ + ||x′n – x′m||1,∞ = ||xn – xm||1,∞, shows that (x′n)n∈N is a Cauchy sequence in (C[a, b], ||·||∞), and hence convergent to say, y ∈ C[a, b]. We will now show that x ∈ C1[a, b], and x′ = y. Let t ∈ [a, b]. By the Fundamental Theorem of Calculus,  and so
and so

Passing the limit as n goes to ∞ gives, for all t ∈ [a, b], 
By the Fundamental Theorem of Calculus, x′ = y ∈ C[a, b]. So x ∈ C1[a, b]. Finally, we’ll show that (xn)n∈N converges to x in C1[a, b]. Let  > 0, and let N be such that for all m, n > N, ||xn – xm||1,∞ <
> 0, and let N be such that for all m, n > N, ||xn – xm||1,∞ <  . Then for all t ∈ [a, b], we have |xn(t) – xm(t)| + |x′n(t) – x′m(t)|
. Then for all t ∈ [a, b], we have |xn(t) – xm(t)| + |x′n(t) – x′m(t)|  |xn – xm|∞ + |x′n – x′m|∞ = ||xn – xm||1,∞ <
|xn – xm|∞ + |x′n – x′m|∞ = ||xn – xm||1,∞ <  . Letting m go to ∞, it follows that for all n > N, |xn(t) – x(t)| + |x′n(t) – x′(t)
. Letting m go to ∞, it follows that for all n > N, |xn(t) – x(t)| + |x′n(t) – x′(t) 
 As the choice of t ∈ [a, b] was arbitrary, it follows that
As the choice of t ∈ [a, b] was arbitrary, it follows that

that is, ||xn – xm||1,∞  2
2 .
.
Let (xn)n∈N be any Cauchy sequence in X. We construct a subsequence (xnk)k∈N inductively, possessing the property that if n > nk, then ||xn – xnk|| < 1/2k, k ∈ N. large enough so that if n, m  n1, then ||xn – xm|| < 1/2. Suppose xn1, ···, xnk have been constructed. Choose nk+1 > nk such that if n, m
n1, then ||xn – xm|| < 1/2. Suppose xn1, ···, xnk have been constructed. Choose nk+1 > nk such that if n, m  nk+1, then ||xn – xm|| < 1/2k+1. In particular for n
nk+1, then ||xn – xm|| < 1/2k+1. In particular for n  nk+1, ||xn – xnk+1|| Z 1/2k+1.
nk+1, ||xn – xnk+1|| Z 1/2k+1.
Now define u1 = xn1, uk+1 = xnk+1 – xnk, k ∈ N.
We have 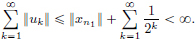 Thus
Thus  converges.
converges.
But the partial sums of  are
are 
So (xnk)k∈N converges in X, to, say x ∈ X. As (xnk)k∈N is a convergent subsequence of the Cauchy sequence (xn)n∈N, it now follows that (xn)n∈N is itself convergent with the same limit x. Indeed, given  > 0, first let N be such that for all n, m > N, ||xn – xm|| <
> 0, first let N be such that for all n, m > N, ||xn – xm|| <  /2, and next let nK > N be such that ||xnK – x|| <
/2, and next let nK > N be such that ||xnK – x|| <  /2, which yields that for all n > N,
/2, which yields that for all n > N,

(N1)For (x, y) ∈ X × Y, ||(x, y)|| = max{||x||, ||y||}  0.
0.
If ||(x, y)|| = 0, then 0  ||x||
||x||  max{||x||, ||y||} = {||x, y)|| = 0, and so ||x|| = 0, giving x = 0. Similarly, y = 0 too, and so (x, y) = 0X×Y.
max{||x||, ||y||} = {||x, y)|| = 0, and so ||x|| = 0, giving x = 0. Similarly, y = 0 too, and so (x, y) = 0X×Y.
(N2)For α ∈ K, and (x, y) ∈ X × Y,
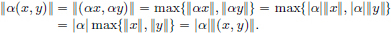
(N3)Let (x1, y1), (x2, y2) ∈ X × Y. Then
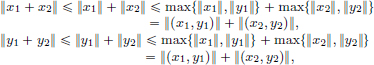
and so max{||x1 + x2||, ||y1 + y2||}  ||(x1, y1)|| + {||x2, y2)||. Thus
||(x1, y1)|| + {||x2, y2)||. Thus
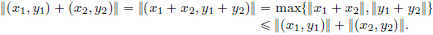
Hence (x, y)  max{||x||, ||y||}, (x, y) ∈ X × Y, defines a norm on X × Y.
max{||x||, ||y||}, (x, y) ∈ X × Y, defines a norm on X × Y.
Let ((xn, yn))n∈N be Cauchy in X × Y. As ||x||  max{||x||, ||y||} = ||(x, y)||, (xn)n∈N is Cauchy in X. As X is Banach, (xn)n∈N converges to some x ∈ X. Similarly (yn)n∈N converges to a y ∈ Y. Let
max{||x||, ||y||} = ||(x, y)||, (xn)n∈N is Cauchy in X. As X is Banach, (xn)n∈N converges to some x ∈ X. Similarly (yn)n∈N converges to a y ∈ Y. Let  > 0. Then there exists an Nx such that for all n > Nx, ||xn – x|| <
> 0. Then there exists an Nx such that for all n > Nx, ||xn – x|| <  , and there is an Ny such that for all n > Ny, ||yn – y|| <
, and there is an Ny such that for all n > Ny, ||yn – y|| <  . So with N := max{Nx, Ny}, for all n > N, we have ||xn – x|| <
. So with N := max{Nx, Ny}, for all n > N, we have ||xn – x|| <  and ||yn – y|| <
and ||yn – y|| <  . Thus ||(xn, yn) – (x, y)|| = ||(xn – x, yn – y)|| = max{||xn – x||, ||yn – y||} <
. Thus ||(xn, yn) – (x, y)|| = ||(xn – x, yn – y)|| = max{||xn – x||, ||yn – y||} <  , showing that ((xn, yn))n∈N converges to (x, y) in X × Y. So X × Y is Banach.
, showing that ((xn, yn))n∈N converges to (x, y) in X × Y. So X × Y is Banach.
Since K is compact in Rd, it is closed and bounded. Let R > 0 be such that for all x ∈ K, ||x||2  R. In particular, for every x ∈ K ∩ F, we have ||x||2
R. In particular, for every x ∈ K ∩ F, we have ||x||2  R. Thus K ∩ F is bounded. Also, since both K and F are closed, it follows that even K ∩ F is closed. Hence K ∩ F is closed and bounded, and so by Theorem 1.10, page 45, we conclude that K∩F is compact.
R. Thus K ∩ F is bounded. Also, since both K and F are closed, it follows that even K ∩ F is closed. Hence K ∩ F is closed and bounded, and so by Theorem 1.10, page 45, we conclude that K∩F is compact.
Clearly Sd–1 is bounded. It is also closed, and we prove this below. Let (xn)n∈N be a sequence in Sd–1 which converges to L in Rd. Let L = (L1, ···, Ld) and  for n ∈ N. Then
for n ∈ N. Then 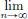 xn(k) = Lk (k = 1, ..., d).
xn(k) = Lk (k = 1, ..., d).
Since xn ∈ Sd–1 for each n ∈ N, we have 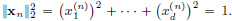 Passing the limit as n → ∞, we obtain
Passing the limit as n → ∞, we obtain  Hence L ∈ Sd–1. So Sd–1 is closed. As Sd–1 is closed and bounded, it follows from Theorem 1.10, page 45, that it is compact.
Hence L ∈ Sd–1. So Sd–1 is closed. As Sd–1 is closed and bounded, it follows from Theorem 1.10, page 45, that it is compact.
(1)Let (Rn)n∈N be a sequence in O(2).
Using  then
then  and
and 
So each of the sequences (an)n∈R, (bn)n∈R, (cn)n∈R, (dn)n∈R is bounded.
By successively refining subsequences of these sequences, we can choose a sequence of indices n1 < n2 < n3 <···, such that the sequences (ank)k∈N, (bnk)k∈N, (cnk)k∈N, (dnk)k∈N are convergent, to, say, a, b, c, d, respectively.
Hence (Rnk)k∈N is convergent with the limit 
From (Rn) Rn = I (n ∈ N), it follows that also R
Rn = I (n ∈ N), it follows that also R R = I, that is, R ∈ O(2).
R = I, that is, R ∈ O(2).
(2)The hyperbolic rotations  belong to O(1, 1) because
belong to O(1, 1) because

But ||R(t)||∞  | cosh(t)| = cosh t → ∞ as t → ∞, showing that O(1, 1) is not bounded. Hence O(1, 1) can’t be compact (as every compact set is necessarily bounded).
| cosh(t)| = cosh t → ∞ as t → ∞, showing that O(1, 1) is not bounded. Hence O(1, 1) can’t be compact (as every compact set is necessarily bounded).
Let  Since K ⊂ [0, 1], clearly K is bounded.
Since K ⊂ [0, 1], clearly K is bounded.
Moreover, 
Thus R\K, being the union of open intervals, is open, that is, K is closed. Since K is closed and bounded, it is compact.
If 1 ∈ C[0, 1] denotes the constant function taking value 1 everywhere, then
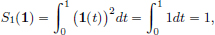
and so 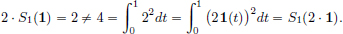
So (L2) is violated, showing that S1 is not a linear transformation.
On the other hand, S2 is a linear transformation. For all x1, x2 ∈ C[0, 1],

and so (L1) holds. Moreover, for all α ∈ R and x ∈ C[0, 1] we have

and so (L2) holds as well.
(1)Let α1, α2 ∈ R be such that α1f1 + α2f2 = 0, that is,

In particular, with t = 0, we obtain α1 = 0. Thus α2eat sin(bt) = 0 for all t ∈ R. With t = π/2b, we see that 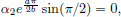 and so α2 = 0. Consequently, f1, f2 are linearly independent.
and so α2 = 0. Consequently, f1, f2 are linearly independent.
(2)First of all, D is a well-defined map from Sf1,f2 to itself, since

Thus DSf1,f2 ⊂ Sf1,f2.
Furthermore, it is clear that D(g1 + g2) = D(g1) + D(g2) for all g1, g2 ∈ C1(R) (and in particular for g1, g2 ∈ Sf1,f2 ⊂ C1(R)), and also D(α · g) = α · D(g) and all g ∈ (R) (and in particular, for all g ∈ Sf1,f2).
Hence D is a linear transformation from Sf1,f2 to itself.
(3)We have Df1 = aeat cos(bt) – eatb sin(bt) = af1 – bf2, and
Df2 = aeat sin(bt) + eatb cos(bt) = bf1 + af2.
So the matrix of D with respect to the basis B = (f1, f2) is 
(4)As det[D]B = a2 + b2 ≠ 0, [D]B is invertible, and 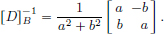
Hence D is invertible, and the inverse D–1 : Sf1,f2 → Sf1,f2 has the matrix [D–1]B (with respect to B) given by [D–1]B = [D]–1]B found above.
(5)We note that 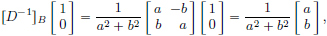 and so
and so

By the definition of D, 
So  any constant.
any constant.
Similarly, as  we have
we have

and so 
So 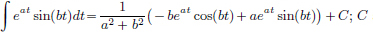 any constant.
any constant.
(1)We have 
(As expected, the arc length is simply the length of the line segment [0, 1].)
(2)We have 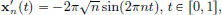 and so
and so
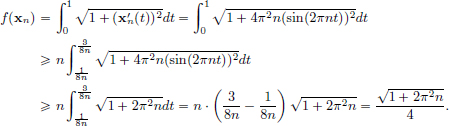
(3)Suppose that f is continuous at 0. Then with  := 1 > 0, there exists a δ > 0 such that whenever x ∈ C1[0, 1] and ||x – 0|| < δ, we have |f(x) – f(0)| < 1.
:= 1 > 0, there exists a δ > 0 such that whenever x ∈ C1[0, 1] and ||x – 0|| < δ, we have |f(x) – f(0)| < 1.
We have  for all
for all 
Hence for such n there must hold that |f(xn) – f(0)| = |f(xn) – 1| < 1.
So for all  we have
we have 
 |f(xn)|
|f(xn)|  |f(xn) – 1| + 1 < 1 + 1 = 2,
|f(xn) – 1| + 1 < 1 + 1 = 2,
which is a contradiction. Hence f is not continuous at 0.
Let x0, x ∈ C1[a, b]. Using the triangle inequality in (R2, ||·||2), we obtain
and so

Thus given  > 0, if we set δ :=
> 0, if we set δ :=  , then we have for all x ∈ C1[0, 1] satisfying ||x – x0||1,∞ < δ that |f(x) – f(x0)|
, then we have for all x ∈ C1[0, 1] satisfying ||x – x0||1,∞ < δ that |f(x) – f(x0)|  ||x – x0||1,∞ < δ =
||x – x0||1,∞ < δ =  .
.
So f is continuous at x0. As the choice of x0 was arbitrary, f is continuous.
Let x0 ∈ X. Given  > 0, set δ :=
> 0, set δ :=  . Then for all x ∈ X satisfying ||x – x0|| < δ, we have | ||x|| – ||x0|| |
. Then for all x ∈ X satisfying ||x – x0|| < δ, we have | ||x|| – ||x0|| |  ||x – x0|| < δ =
||x – x0|| < δ =  . Thus ||·|| is continuous at x0. As x0 ∈ X was arbitrary, it follows that ||·|| is continuous on X.
. Thus ||·|| is continuous at x0. As x0 ∈ X was arbitrary, it follows that ||·|| is continuous on X.
f–1({–1, 1}) = {nπ : n ∈ Z}, f–1({1}) = {2nπ : n ∈ Z}, f–1([–1, 1]) = R, and 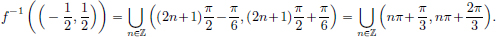
Since cos is periodic with period 2π (that is, f(x) = f(x + 2π) for all x ∈ R), we have f(R) = f([0, 2π]) = f([δ, δ + 2π]) = [–1, 1].
(“If” part) Suppose that for every closed F in Y, f–1(F) is closed in X.
Now let V be open in Y. Then Y\V is closed in Y.
Thus f–1(Y\V) = f–1(Y)\f–1(V) = X\f–1(V) is closed in X.
Hence f–1(V) = X\(X\f–1(V)) is open in X.
So for every open V in Y, f–1(V) is open in X.
By Theorem 2.1, page 63, f is continuous on X.
(“Only if” part) Suppose that f is continuous.
Let F be closed in Y, that is, Y\F is open in Y.
Hence f–1(Y\F) = f–1(Y\f–1(F) = X\f–1(F) is open in X.
Consequently, we have that f–1(F) is closed in X.
If x ∈ (g  f)–1(W), then (g
f)–1(W), then (g  f)(x) ∈ W, that is, g(f(x)) ∈ W. So f(x) ∈ g–1(W), that is, x ∈ f–1(g–1(W)). Thus (g
f)(x) ∈ W, that is, g(f(x)) ∈ W. So f(x) ∈ g–1(W), that is, x ∈ f–1(g–1(W)). Thus (g  f)–1(W) ⊂ f–1 (g–1(W)).
f)–1(W) ⊂ f–1 (g–1(W)).
If x ∈ f–1(g–1(W)), then f(x) ∈ g–1(W), that is, (g  f)(x) = g(f(x)) ∈ W. Hence x ∈ (g
f)(x) = g(f(x)) ∈ W. Hence x ∈ (g  f)–1(W). So we have f–1(g–1(W)) ⊂ (g
f)–1(W). So we have f–1(g–1(W)) ⊂ (g f)–1(W).
f)–1(W).
Consequently, (g  f)–1(W) = f–1(g–1(W)).
f)–1(W) = f–1(g–1(W)).
(1)True.
Since (–∞, 1) is open in R and f : X → R is continuous, it follows that {x ∈ X : f(x) < 1} = f–1(–∞, 1) is open in X by Theorem 2.1, page 63.
(2)True.
Because (1, ∞) is open in R, and f : X → R is continuous, it follows by Theorem 2.1, page 63, that {x ∈ X : f(x) > 1} = f–1 (1, ∞) is open in X.
(3)False.
Take for example X = R with the usual Euclidean norm, and consider the continuous function f(x) = x for all x ∈ R. Then {x ∈ X : f(x) = 1} = {1}, which is not open in R.
(4)True.
(–∞, 1] is closed in R because its complement is (1, ∞), which is open in R. As f : X → R is continuous, {x ∈ X : f(x)  1} = f–1 (–∞, 1] is closed in X by Corollary 2.1, page 64.
1} = f–1 (–∞, 1] is closed in X by Corollary 2.1, page 64.
(5)True.
Since {1} is closed in R and since f : X → R is continuous, it follows by Corollary 2.1, page 64, that {x ∈ X : f(x) = 1} = f–1{1} is closed in X.
(6)True.
Each of the sets f–1{1} and f–1{2} are closed, and so their finite union, namely {x ∈ X : f(x) = 1 or 2} is closed as well.
(7)False.
Take for example X = R with the usual Euclidean norm, and consider the continuous function f(x) = 1 (x ∈ R). Then {x ∈ X : f(x) = 1} = R, which is not bounded, and hence can’t be compact.
For all x ∈ X, we have f(2x) = –f(x), and so

Since the sequence 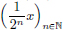 converges to 0, it follows that
converges to 0, it follows that
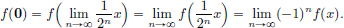
So we obtain that ((–1)nf(x))n∈N is convergent with limit f(0). Thus the subsequence (f(x))n∈N = ((–1)2nf(x))n∈N of ((–1)f(x))n∈N is also convergent with limit f(0). Hence f(x) = f(0) for all x ∈ X. As f(0) = f(2 · 0) = –f(0), it follows that f(0) = 0. Hence f(x) = 0 for all x ∈ X. So if f is continuous and it satisfies the given identity then it must be the constant function x  0 : X → Y.
0 : X → Y.
Conversely, the constant function x  0 : X → Y is indeed continuous and also f(2x) + f(x) = 0 + 0 = 0 for all x ∈ X.
0 : X → Y is indeed continuous and also f(2x) + f(x) = 0 + 0 = 0 for all x ∈ X.
The determinant of M = [mij] is given by the sum of expressions of the type

where p : {1, 2, 3, ···, n} → {1, 2, 3, ···, n} is a permutation. Since each of the maps M  m1p(1) m2p(2) m3p(3) ... mnp(n) is easily seen to be continuous using the characterisation of continuous functions provided by Theorem 2.3, page 64, it follows that their linear combination is also continuous.
m1p(1) m2p(2) m3p(3) ... mnp(n) is easily seen to be continuous using the characterisation of continuous functions provided by Theorem 2.3, page 64, it follows that their linear combination is also continuous.
{0} is closed in R, and so its inverse image det–1{0} = {M ∈ Rn×n : det M = 0} under the continuous map det is also closed. Thus its complement, namely the set {M ∈ Rn×n : det M ≠ 0}, is open. But this is precisely the set of invertible matrices, since M ∈ Rn×n is invertible if and only if det M ≠ 0.
We’d seen in Exercise 1.21, page 21, that a singleton set in any normed space is closed. So {0} is closed in Rm. As the linear transformation TA : Rn → Rm is continuous, its inverse image under TA, T–1A({0}) = {x ∈ Rn : Ax = 0} = ker A, is closed in Rn.
Let V be a subspace of Rn, and let {v1, · · ·, vk} be a basis for V. Extend this to a basis {v1, · · ·, vk, vk+1, · · ·, vn} for R. By using the Gram-Schmidt orthogonalisation procedure, we can find an orthonormal5 set of vectors {u1, · · ·, un} such that for each k ∈ {1, · · ·, n}, the span of the vectors v1, · · ·, vk coincides with the span of u1, · · ·, uk. Now define A ∈ R(n–k)×n as follows:

It is clear from the orthonormality of the ujs that Au1 = · · · = Auk = 0, and so it follows that also any linear combination of u1, · · ·, uk lies in the kernel of A. In other words, V ⊂ ker A.
On the other hand, if x = α1u1 + · · · + αnun, where α1, · · ·, αn are scalars and if Ax = 0, then it follows that

So x = α1u1 + · · · + αkuk ∈ V. Hence ker A ⊂ V.
Consequently V = ker A, and by the result of the previous exercise, it now follows that V is closed.
(1)The linearity of T follows immediately from the properties of the Riemann integral. Continuity follows from the straightforward estimate

(2)The partial sums sn of the series converge to f. Thus, since the continuous map T preserves convergent sequences, it follows that

We have for all t ∈ R that
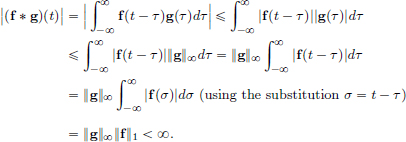
Thus ||f ∗ g||∞  ||g||∞||f||1 for all g ∈ L∞(R). So f∗ is well-defined. Linearity is easy to see. From the above estimate, it follows that the linear transformation f∗ is continuous as well.
||g||∞||f||1 for all g ∈ L∞(R). So f∗ is well-defined. Linearity is easy to see. From the above estimate, it follows that the linear transformation f∗ is continuous as well.
Consider the reflection map  : L2(R) → L2(R). Then it is straightforward to check that R ∈ L(L2(R)), and moreover it is continuous since ||f||2 =
: L2(R) → L2(R). Then it is straightforward to check that R ∈ L(L2(R)), and moreover it is continuous since ||f||2 =  2 for all f ∈ L2(R). Clearly Y = ker(I – R), and so, being the inverse image of the closed set {0} under the continuous map I – R, it follows that Y is closed.
2 for all f ∈ L2(R). Clearly Y = ker(I – R), and so, being the inverse image of the closed set {0} under the continuous map I – R, it follows that Y is closed.
For 

and so Λ ∈ CL(ℓ2) and ||Λ|| 
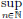 |λn|.
|λn|.
Moreover, for ℓ2 ∋ en := (0, · · ·, 0, 1, 0, · · ·) ∈ ℓ2 (sequence with all terms equal to 0 and nth term equal to 1), we have

for all n, and so ||Λ|| is an upper bound for {|λn| : n ∈ N}. Hence ||Λ|| 
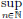 |λn|.
|λn|.
From the above, it now follows that ||Λ|| = 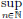 |λn|.
|λn|.
If λn = 1 –, 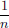 n ∈ N, then ||Λ|| =
n ∈ N, then ||Λ|| = 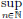
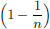 = 1.
= 1.
Suppose that x = (an)n∈N ∈ ℓ2 is such that ||x||2  1 and ||Λx||2 = ||Λ|| = 1.
1 and ||Λx||2 = ||Λ|| = 1.
If 0 = a2 = a3 = · · ·, then Λx = 0, and this contradicts the fact that ||Λx||2 = 1.
So at least one of the terms a2, a3, · · · must be nonzero.
a contradiction. So the operator norm is not attained for this particular Λ.
Let x = (xn)n∈N ∈ ℓp, and let  > 0.
> 0.
Then there exists an N such that  |xk|p <
|xk|p <  p. Let sn :=
p. Let sn := 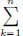 xkek.
xkek.
Then for n > N, x – sn = (0, · · ·, 0, xn+1, xn+2, xn+3, · · ·).
So  giving ||x – sn||p <
giving ||x – sn||p <  .
.
So (sn)n∈N converges in ℓp to x, that is, x =  xnen.
xnen.
The map x = (x1, x2, x3, · · ·)  xn : ℓp → K is easily seen to be linear.
xn : ℓp → K is easily seen to be linear.
It’s continuous as for all x ∈ ℓp, |φn(x)| = |xn| = (|xn|p)1/p  = |x|p.
= |x|p.
If x =  , where the ξis and
, where the ξis and  s are scalars, then applying φn,
s are scalars, then applying φn,

As the choice of n was arbitrary, ξn =  for all n.
for all n.
(1)Let x = (xn)n∈N ∈ ℓ∞. Then for all n ∈ N, |xn|  ||x|∞.
||x|∞.
Thus  = ||x||∞.
= ||x||∞.
Consequently Ax ∈ ℓ∞. So A is a well-defined map.
The linearity is easy to check.
Also, we see that for all x ∈ ℓ∞ that ||Ax||∞ = 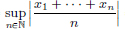
 ||x||∞.
||x||∞.
So A ∈ CL(ℓ∞), and ||A||  1. Also, with 1 := (1, 1, 1, · · ·) ∈ ℓ∞, we have
1. Also, with 1 := (1, 1, 1, · · ·) ∈ ℓ∞, we have
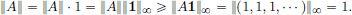
Consequently, ||A|| = 1.
(2)Let x = (xn)n∈N ∈ c, and let its limit be denoted by L.
We’ll show that Ax ∈ c as well.
We will prove that Ax is convergent with the same limit L! (Intuitively, this makes sense since for large n, all xns look alike,  L, and the average of these is approximately L, since the first few terms do not “contribute much” if we take a large collection to take an average.)
L, and the average of these is approximately L, since the first few terms do not “contribute much” if we take a large collection to take an average.)
Let  > 0. Then there exists an N1 ∈ N such that for all n > N1, |xn – L| <
> 0. Then there exists an N1 ∈ N such that for all n > N1, |xn – L| <  /2. Since (xn)n∈N is convergent, it is bounded, and so there exists an M > 0 such that for all n ∈ N, |an|
/2. Since (xn)n∈N is convergent, it is bounded, and so there exists an M > 0 such that for all n ∈ N, |an|  M.
M.
Choose N ∈ N such that N > max 
(This ghastly choice of N is arrived at by working backwards. Since we wish to make  less than
less than  for n > N, we manipulate this, as shown in the chain of inequalities below, and then choose N large enough to achieve this.)
for n > N, we manipulate this, as shown in the chain of inequalities below, and then choose N large enough to achieve this.)
So N > N1 and  Then for all n > N, we have:
Then for all n > N, we have:
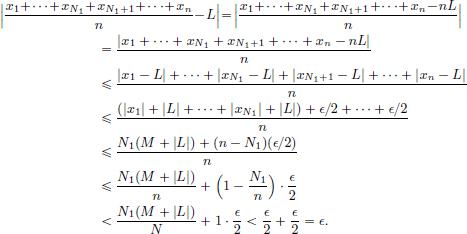
So  is a convergent sequence with limit L.
is a convergent sequence with limit L.
Hence Ax ∈ c. Consequently Ac ⊂ c, and c is an invariant subspace of A.
(If part:) Since  |λn| > 0, we have |λk|
|λn| > 0, we have |λk| 
 |λn| > 0, and so λk ≠ 0 for all k.
|λn| > 0, and so λk ≠ 0 for all k.
Moreover,  < ∞, and so V : ℓ2 → ℓ2 given by
< ∞, and so V : ℓ2 → ℓ2 given by

belongs to CL(ℓ2). Moreover for all (an)n∈N we have

and so VΛ = I = ΛV. Hence Λ is invertible in CL(ℓ2), with Λ–1 = V.
(Only if part:) Let Λ be invertible in CL(ℓ2). Then there exists a Λ–1 ∈ CL(ℓ2) such that Λ–1Λ = I = ΛΛ–1. So ||x||2 = ||Λ–1Λx||2  ||Λ–1||||Λx||2, for all x ∈ ℓ2.
||Λ–1||||Λx||2, for all x ∈ ℓ2.
Hence ||Λx||2 
 for all x ∈ ℓ2. So with x := ek (kth term 1, others 0),
for all x ∈ ℓ2. So with x := ek (kth term 1, others 0),

Thus 
We have
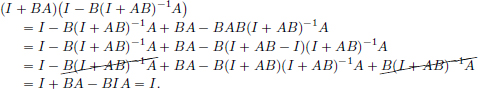
Similarly,
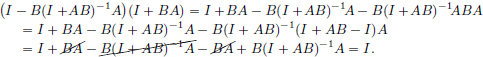
(1)If there exist matrices A, B such that AB – BA = I, then

a contradiction.
(2)If n = 1, then ABn – BnA = AB – BA = I = 1 · B0 = nBn–1.
If for some n ∈ N, we have ABn – BnA = nBn–1, then

and so the result follows by induction.
Suppose that AB – BA = I. Then for all n ∈ N, ABn – BnA = nBn–1. Taking operator norm on both sides yields

We claim that Bn–1 ≠ 0 for all n ∈ N. Indeed, if n = 1, then B0 := I ≠ 0. If Bn–1 ≠ 0 for some n ∈ N, then Bn = 0 gives the contradiction that

and so we must have Bn ≠ 0 too. By induction, our claim is proved. Thus in (7.3), we may cancel ||Bn−1|| > 0 on both sides of the inequality, obtaining n  2||A||||B|| for all n ∈ N, which is absurd. Consequently, our original assumption that AB − BA = I must be false.
2||A||||B|| for all n ∈ N, which is absurd. Consequently, our original assumption that AB − BA = I must be false.
(3)If Ψ ∈ C∞(R), then
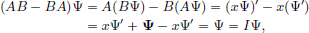
and so AB − BA = I.
Solution to Exercise 2.23, page 87
(1)For x = (x1, x2) ∈ R2, we have, using the Cauchy-Schwarz inequality, that

So 
By the Neumann Series Theorem, (I − K)−1 exists in CL(R2).
So there is a unique solution x ∈ R2 to (I − K)x = y, given by x = (I − K)−1y.
(2)We have 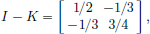 and so
and so 
Thus 
(3)A computer program yielded the following numerical values:

Solution to Exercise 2.24, page 88
If n = 1, then (I − A)P1 = (I − A)(I + A)(I + A2) = I − A4 = I − A21 + 1.
If the claim is true for some k ∈ N, then
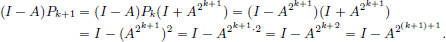
So the claim follows by induction for all n ∈ N.
(I − A2n+1)n∈N converges to I in L(X) since ||A|| < 1 and

Also, since ||A|| < 1, I − A is invertible in CL(X). We have

and so ((I − A)−1 (I − A2n+1))n∈N = ((I − A)−1(I − A)Pn)n∈N = (Pn)n∈N is convergent with limit (I − A)−1.
Solution to Exercise 2.25, page 88
(1)Let T0 ∈ GL(X). Then T0−1 ∈ CL(X), and also r := ||T0−1|| ≠ 0.
If T ∈  , and in particular,
, and in particular,

and so by the Neumann Series Theorem, I + (T − T0)T0−1 belongs to GL(X).
But as T0 ∈ GL(X) too, it now follows that

This completes the proof that GL(X) is an open subset of CL(X).
(2)Let T0 ∈ GL(X) and  > 0. Set
> 0. Set 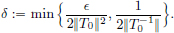
Let T ∈ CL(X) be such that ||T − T0|| < δ.
Then in particular ||T −  and so by part (1), T ∈ GL(X), with
and so by part (1), T ∈ GL(X), with
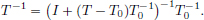
Moreover, we have
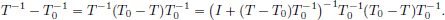
Thus using the estimate from the Neumann Series Theorem,

Solution to Exercise 2.26, page 92
A2 = B2 = 0, and so A, B are nilpotent.
Hence  and
and 
We note that 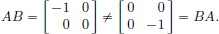
Also, 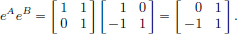
We have  and
and  Thus
Thus
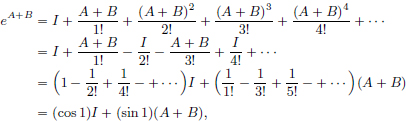
and so 
Solution to Exercise 2.27, page 94
Suppose that the Banach space has an infinite countable Hamel basis {x1, x2, x3, ··· }. We can ensure that for all n ∈ N, we have ||xn|| = 1. Let Fn := span{x1, x2, ···, xn}. Then each Fn is a finite dimensional normed space (with the induced norm from X), and so it is a Banach space. It follows that Fn is a closed subspace of X. By the Baire Lemma, there is an n ∈ N such that Fn contains an open set U, and in particular, an open ball B(X, 2r) for some r > 0. The vector y := rxn+1 + x belongs to B(X, 2r) since ||y − x|| = ||rxn+1|| = r < 2r. Since y, x ∈ B(X, 2r) ⊂ Fn, and as Fn is a subspace, we conclude that (y − x)/r ∈ Fn too, that is, xn+1 ∈ Fn = span{x1, ···, xn}, a contradiction.
Solution to Exercise 2.28, page 96
In light of the Open Mapping Theorem, such a function must necessarily be nonlinear. If the function is constant on an open interval I, then the image f(I) will be a singleton, which is not closed. The following function does the job:

If I := (−1, 1), then f(I) = {0}, which is not open. f is surjective and continuous, and its graph is depicted in the following picture.
Solution to Exercise 2.29, page 96
From Exercise 1.38, page 44, X × Y is a Banach space. Since G(T) is a closed subspace of the Banach space X × Y, it is a Banach space too. Let us now consider the map p : G(T) → X defined by p(X, Tx) = x for x ∈ X. Then p is a linear transformation:

for α ∈ K, x, x1, x2 ∈ X. Moreover, p continuous because

p is also injective since if p(X, Tx) = 0, then x = 0.
Furthermore, if x ∈ X, then x = p(x, Tx), showing that p is surjective too.
Thus, p ∈ CL(G(T), X) is bijective, and hence invertible in CL(G(T), X), with inverse p−1 ∈ CL(X, G(T)). Hence for all x ∈ X,

showing that T ∈ CL(X, Y).
Solution to Exercise 2.30, page 102
We have

Solution to Exercise 2.31, page 102
(1)We know that σ (T) ⊂ {λ ∈ C : |λ|  ||T||}, and so ||T|| is an upper bound for {|λ| : λ ∈ σ(T)}. Thus
||T||}, and so ||T|| is an upper bound for {|λ| : λ ∈ σ(T)}. Thus 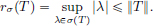
(2)We have σ(TA) = {eigenvalues of A} = {1}, and so rσ(TA) = 1.
On the other hand, with  we have ||x1||2 = 1, and so
we have ||x1||2 = 1, and so

Solution to Exercise 2.32, page 103
Suppose that λ2 ∉ σ(T2). Then λ2 ∈ ρ(T2), that is, λ2 I − T2 is invertible in CL(X). From the identity (λ2I − T2) = (λI − T)(λI + T) = (λI + T)(λI − T), we then obtain 
But then Q = QI = Q(λI − T)P = IP = P, and so P = Q ∈ CL(X) is the inverse of λI − T, a contradiction to the fact that λ ∈ σ(T).
Solution to Exercise 2.33, page 103
If en ∈ ℓ2 denotes the sequence with the nth term equal to 1, and all others equal to 0, then Λen = λnen, and so each λn is an eigenvalue of Λ with eigenvector en ≠ 0. Thus {λn : n ∈ N} ⊂ σp(Λ).
Next we will show that σ(Λ) ⊂ {λn : n ∈ N} {0}. To this end, suppose that μ ∉ {λn : n ∈ N}
{0}. To this end, suppose that μ ∉ {λn : n ∈ N} {0}. Then we claim that μI − Λ is invertible in CL(ℓ2). By a previous exercise, we know that in order to show the invertibility of
{0}. Then we claim that μI − Λ is invertible in CL(ℓ2). By a previous exercise, we know that in order to show the invertibility of
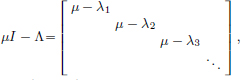
it is enough to show that |μ − λn| is bounded away from 0. To see this, note that since  there is an N large enough such that |λn| < |μ|/2 for all n > N, and so
there is an N large enough such that |λn| < |μ|/2 for all n > N, and so
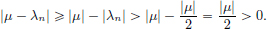
But also |μ − λ1|, ···, |μ − λN| are all positive, so that we do have

Hence μI − Λ ∈ CL(ℓ2) is invertible in CL(ℓ2), that is, μ ∈ ρ(Λ).
Thus σ(Λ) ⊂ {λn : n ∈ N} {0}.
{0}.
But the spectrum σ(Λ) is closed, and since it contains σp(Λ) ⊃ {λn : n ∈ N}, it must contain the limit of (λn)n∈N, which is {0}.
So we also obtain {λn : n ∈ N} {0} ⊂ σp(Λ)
{0} ⊂ σp(Λ) {0} ⊂ σ(Λ).
{0} ⊂ σ(Λ).
Thus σ(Λ) = {λn : n ∈ N} {0}.
{0}.
Consequently, {λn : n ∈ N} ⊂ σp(Λ) ⊂ {λn : n ∈ N} {0} = σ(Λ).
{0} = σ(Λ).
Solution to Exercise 2.34, page 103
(1)Suppose that λ ∈ σap(T). Then there exists a sequence (xn)n∈C of vectors in X such that ||xn|| = 1 for all n ∈ N, and 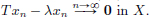
We will just prove that λ ∉ ρ(T), and so by definition it will follow that then λ ∈ σ(T). Suppose, on the contrary, that λ ∈ ρ(T). Then T − λI is invertible in CL(X). Thus

a contradiction. Consequently, λ ∉ ρ(T), that is, λ ∈ σ(T).
(2)For k ∈ N, let ek denote the sequence in ℓ2 whose kth term is 1 and all other terms are zeros. Then ||ek||2 = 1, and Λek = λkek, so that

that is,  Consequently,
Consequently, 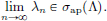
Solution to Exercise 2.35, page 103
Let λ ∈ C and Ψ ∈ DQ be such that xΨ(x) = λΨ(x) for almost all x ∈ R, that is, (x − λ)Ψ(x) = 0 for almost all x ∈ R. Now x − λ ≠ 0 for all x ∈ R\{λ}. Hence for almost all x ∈ R, Ψ(x) = 0, that is, Ψ = 0 in L2(R). Consequently, λ can’t be an eigenvalue of Q, and so σp(Q) = ∅.
Solution to Exercise 2.36, page 105
For simplicity we’ll assume K = R. If a = (an)n∈N ∈ ℓ1, then define the functional φa ∈ CL(c0, R) = (c0)′ by

Then a  φa : ℓ1 → (c0)′ is an injective linear transformation, and it is also continuous because |φa(b)|
φa : ℓ1 → (c0)′ is an injective linear transformation, and it is also continuous because |φa(b)|  ||b||∞ ||a||1 for all b ∈ c0, and ||φa||
||b||∞ ||a||1 for all b ∈ c0, and ||φa||  ||a||1. To see the surjectivity of this map, we need to show that given φ ∈ (c0)′, there exists an a ∈ ℓ1 such that φ = φa. Let en ∈ c0 being the sequence with nth term 1 and all others 0. Set a = (φ(e1), φ(e2), φ(e3), ···). We’ll show that a ∈ ℓ1, and that φ = φa.
||a||1. To see the surjectivity of this map, we need to show that given φ ∈ (c0)′, there exists an a ∈ ℓ1 such that φ = φa. Let en ∈ c0 being the sequence with nth term 1 and all others 0. Set a = (φ(e1), φ(e2), φ(e3), ···). We’ll show that a ∈ ℓ1, and that φ = φa.
Define the scalars αn, n ∈ N, by 
Then for all n we have αnφ(en) = |φ(en)|.
We have ||(α1, ···, αn, 0, ···)||∞  1, and so
1, and so

for all n ∈ N. Hence a ∈ ℓ1.
Finally, we need to show φ = φa . Let b = (bn)n∈N ∈ c0 and  > 0. Then there exists an N such that for all n > N, |bn| <
> 0. Then there exists an N such that for all n > N, |bn| <  . Set b
. Set b = (b1, ···, bN, 0, ···) ∈ c0. Then ||b − b
= (b1, ···, bN, 0, ···) ∈ c0. Then ||b − b ||∞ = ||(0, ··· , 0, bN+1, ···)||∞
||∞ = ||(0, ··· , 0, bN+1, ···)||∞ 
 . Moreover, we have that
. Moreover, we have that
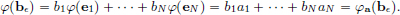
Hence

As the choice of  > 0 was arbitrary, it follows that φ(b) = φa(b) for all b ∈ c0, that is, φ = φa.
> 0 was arbitrary, it follows that φ(b) = φa(b) for all b ∈ c0, that is, φ = φa.
Solution to Exercise 2.37, page 105
(1)BV [a, b] is a vector space: We prove that BV [a, b] is a subspace of the vector space R[a,b] of all real valued functions on [a, b] with pointwise operations.
(S1)The zero function 0 belongs to BV [a, b].
Indeed, for any partition 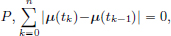 and so var(0) = 0 < ∞.
and so var(0) = 0 < ∞.
(S2)Let μ1, μ2 ∈ BV [a, b]. Then we have

and so μ1 + μ2 ∈ BV [a, b].
(S3)Let α ∈ R and μ ∈ BV [a, b]. Then

and so αμ ∈ BV [a, b].
(2)We show that μ  ||μ|| defines a norm on BV [a, b].
||μ|| defines a norm on BV [a, b].
(N1)If μ ∈ BV [a, b], then ||μ|| = |μ(a)| + var(μ)  0.
0.
Let μ ∈ BV [a, b] be such that ||μ|| = 0. Then var(μ) = 0, and |μ(a)| = 0.
Hence μ(a) = 0. Suppose that μ ≠ 0. Then there exists a c ∈ [a, b] such that μ(c) ≠ 0. Clearly c ≠ a, since μ(a) = 0. Now consider the partition
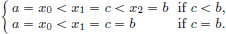
Then var 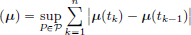
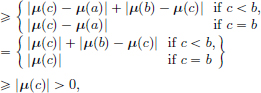
a contradiction. Hence μ = 0.
(N2)Let α ∈ R and μ ∈ BV [a, b]. Then αμ ∈ BV [a, b], and we have seen earlier that varαμ = |α|var(μ). Hence

(N3)Let μ1, μ2 ∈ BV [a, b]. Then μ1 + μ2 ∈ BV [a, b], and we’ve seen above that var(μ1 + μ2)  var(μ1) + var(μ2). Thus
var(μ1) + var(μ2). Thus
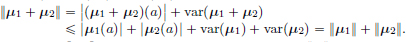
Consequently BV [a, b] is a normed space with the norm ||·||.
(3)Let x ∈ C[a, b] and μ ∈ BV [a, b]. Given  > 0, let δ > 0 be such that for every partition P satisfying δP < δ, we have
> 0, let δ > 0 be such that for every partition P satisfying δP < δ, we have

Then

As the choice of  > 0 was arbitrary, it follows that
> 0 was arbitrary, it follows that 
(4)For all x ∈ C[a, b], |φµx|  ||x||∞ var(μ).
||x||∞ var(μ).
From the linearity of the Riemann-Stieltjes integral, it follows that φµ is a linear transformation from C[a, b] to R. From the above estimate, we also see that φµ is continuous. Consequently φµ ∈ CL(C[a, b), R) = (C[a, b])′.
Moreover ||φµ||  var(μ).
var(μ).
(5)We will show that (x  x(a)) = φµ, where
x(a)) = φµ, where 
First of all, μ ∈ BV [a, b], since var(μ) = 1 < ∞.
Let x ∈ C[a, b], and  > 0. Let δ > 0 be such that for all t such that t − a < δ, we have |x(t) − x(a)| <
> 0. Let δ > 0 be such that for all t such that t − a < δ, we have |x(t) − x(a)| <  .
.
Then for all partitions P with δP < δ, we have

where the last inequality follows from the fact that |a − t1|  δP < δ.
δP < δ.
So  (μ is not unique: for any c ∈ R, μ + c also works!)
(μ is not unique: for any c ∈ R, μ + c also works!)
Solution to Exercise 2.38, page 109
On the one dimensional subspace Y :=span{x∗} ⊂ X, we have a continuous linear map φ : Y → C. (Simply define φ(αx∗) = α, then |φ(αx∗)| = |α| = ||αx∗||/||x∗||, and so ||φ|| = 1/||x∗|| < ∞.) By the Hahn-Banach Theorem, there exists an extension φ∗ ∈ CL(X, C) of φ, and so φ∗(x∗) = φ(x∗) = 1 ≠ 0. (Alternatively, one could just use Corollary 2.7, page 109, with x = x∗ and y = 0: there exists a functional φ∗ ∈ CL(X, C) such that φ∗(x∗) ≠ φ∗(0) = 0.)
Solution to Exercise 2.39, page 115
Consider the collection P of all linearly independent subsets S ⊂ X. Consider the partial order which is simply set inclusion ⊂. Then every chain in P has an upper bound, as explained below.
If C is a chain in P, then  is an upper bound of C.
is an upper bound of C.
We just need to show the linear independence of this set U. To this end, let v1, ···, vn be any set of vectors from U for which there exist scalars α1, ···, αn in F such that α1v1 + ··· + αnvn = 0. Let the sets S1, ···, Sn ∈ C be such that v1 ∈ S1, ···, vn ∈ Sn. As C is a chain, we can arrange the finitely many Sks in “ascending order”, and there exists a k∗ ∈ {1, ···, n} such that S1, ···, Sn ⊂ Sk∗. Then v1, ···, vn ∈ Sk∗. But by the linear independence of Sk∗, we conclude that α1 = ··· = αn = 0. Thus U is linearly independent, showing that every chain in P has an upper bound.
By Zorn’s Lemma, P has a maximal element B. We claim that span B = X. For if not, then there exists an x ∈ X\span B. We will show B′ := B ∪ {x} is linearly independent. Suppose that α1, ···, αn, α ∈ K and v1, ···, vn ∈ B are such that αx + α1v1 + ··· + αnvn = 0. First we note that α = 0, since otherwise

which is false. As α = 0, the equality αx + α1v1 + ··· + αnvn = 0 now becomes α1v1 + ··· + αnvn = 0. But by the independence of the set B, we conclude that α1 = ··· = αn = 0 too. Hence B′ is linearly independent, and so B′ belongs to P. As B′ = B ∪ {x}  B, we obtain a contradiction (to the maximality of B). Consequently, span B = X, and as B ∈ P, B is also linearly independent.
B, we obtain a contradiction (to the maximality of B). Consequently, span B = X, and as B ∈ P, B is also linearly independent.
Solution to Exercise 2.40, page 115
Let B = {vi : i ∈ I}. Every x ∈ X has a unique decomposition

for some finite number of indices i1, ···, in ∈ I and scalars α1, ···, αn in F. Define F(x) = α1f(vi1) + ··· + αnf(vin). It is clear that F(vi) = f(vi), i ∈ I. Let us check that F : X → Y is linear.
(L1)Given x1, x2 ∈ X, there exist scalars α1, ···, αn and β1, ···, βn (possibly several of them equal to zero) and indices i1, ···, in ∈ I, such that

(L2)Let α ∈ F. Given x ∈ X, there exist β1, ··· , βn ∈ F and i1, ···, in ∈ I, such that x = β1vi1 + ··· + βnvin. Then αx = (αβ1)vi1 + ··· + (αβn)vin.

Solution to Exercise 2.41, page 115
Let B be a Hamel basis for X. As X is infinite dimensional, B is an infinite set. Let {vn : n ∈ N} be a countable subset of B. Let y∗ ∈ Y be any nonzero vector.
Let f : B → Y be defined by 
By the previous exercise, this f extends to a linear transformation F from X to Y. We claim that F ∉ CL(X, Y). Suppose that it does. Then there exists an M > 0 such that for all x ∈ X, ||F(x)||  M||x||. But if we put x = vn, n ∈ N, this yields n||vn||||y∗|| = ||f(vn)|| = ||F(vn)||
M||x||. But if we put x = vn, n ∈ N, this yields n||vn||||y∗|| = ||f(vn)|| = ||F(vn)||  M ||vn||, and so for all n ∈ N, n
M ||vn||, and so for all n ∈ N, n  M/||y∗||, which is absurd. Thus F is a linear transformation from X to Y, but is not continuous.
M/||y∗||, which is absurd. Thus F is a linear transformation from X to Y, but is not continuous.
Solution to Exercise 2.42, page 115
If R were finite dimensional, say d-dimensional over Q, then there would exist a one-to-one correspondence between R and Qd. But Qd is countable, while R isn’t, a contradiction. So R is an infinite dimensional vector space over Q.
Suppose that R has a countable basis B = {vn : n ∈ N} over Q.
We will define an injective map 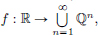 yielding a contradiction.
yielding a contradiction.
Set f(0) := 0 ∈ Q1. If x ≠ 0, then x has a decomposition x = q1v1 + ··· + qnvn, where q1, ···, qn ∈ Q and qn ≠ 0. In this case, set f(x) = (q1, ···, qn) ∈ Qn. It can be seen that if f(x) = f(y), for some x, y ∈ R, then x = y. So f is injective.
As  is countable, follows that R is countable too, a contradiction.
is countable, follows that R is countable too, a contradiction.
Hence B can’t be countable.
Solution to Exercise 2.43, page 115
The set R is an infinite dimensional vector space over Q. Let {vi : i ∈ I} be a Hamel basis for this vector space. Fix any i∗ ∈ I.
We define a function f : B → R on the basis elements: 
Let F be an extension of f from B to R, as provided by Exercise 2.40, page 115. Then F is linear, and in particular, additive. So F(x + y) = F(x) + F(y) for all x, y ∈ R.
We now show that F is not continuous on R: for otherwise, for any vi ≠ vi∗, if (qn)n∈N is a sequence in Q converging to the real number vi/vi∗ (vi∗ ≠ 0 since it is a basis vector), then we would have

a contradiction!
Solution to Exercise 2.44, page 116
(1)By the Algebra of Limits, the map l is linear.
Let (xn)n∈N ∈ c. For all n ∈ N, |xn|  ||(xn)n∈N||∞.
||(xn)n∈N||∞.
Passing the limit as 
Thus l ∈ CL(c, K).
(2)Y is a subspace of ℓ∞. Indeed we have:
(S1)Clearly (0)n∈N ∈ Y, since 
(S2)Let (xn)n∈N, (yn)n∈N ∈ Y.
Then 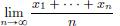 and
and  exist.
exist.
As 
we conclude that  exists as well.
exists as well.
Thus (xn)n∈N + (yn)n∈N ∈ Y too.
(S3)Let (xn)n∈N ∈ Y and α ∈ K. Then  exists.
exists.
As  it follows that
it follows that
 exists, and so α · (xn)n∈N ∈ Y.
exists, and so α · (xn)n∈N ∈ Y.
Consequently, Y is a subspace of ℓ∞.
(3)For all x ∈ ℓ∞, x − Sx ∈ Y : Let x = (xn)n∈N ∈ ℓ∞. Then we have

We have 
As x ∈ ℓ∞, it follows that  and so x − Sx ∈ Y.
and so x − Sx ∈ Y.
(4)If x = (xn)n∈N ∈ c, then Ax ∈ c, where A denotes the averaging operator (Exercise 2.19, page 77).
Hence 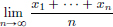 exists, and so x ∈ Y. Consequently, c ⊂ Y.
exists, and so x ∈ Y. Consequently, c ⊂ Y.
(5)Define L0 : Y → K by L0(xn)n∈N = 
Then it is easy to check that L0 : Y → K is a linear transformation.
Moreover, if x ∈ Y, then 
But 
Hence |L0x|  ||x||∞. Consequently, L0 ∈ CL(Y, K).
||x||∞. Consequently, L0 ∈ CL(Y, K).
We had seen that if x ∈ c, then Ax ∈ c, and that l(Ax) = l(x).
Hence for all x ∈ c, L0(x) = l(Ax) = l(x), that is, L0|c = l.
Using the Hahn-Banach Theorem, there exists an L ∈ CL(ℓ∞, K) such that L|Y = L0 (and ||L|| = ||L0||).
In particular, if x ∈ c, then x ∈ Y and so Lx = L0x = lx. Thus L|c = l.
Also, if x = (xn)n∈N ∈ ℓ∞, then x − Sx ∈ Y.
Thus Lx = LSx for all x ∈ ℓ∞, that is, L = LS.
(6)We have 

Consequently, 
Solutions to the exercises from Chapter 3
Solution to Exercise 3.1, page 124
f is a continuous linear transformation. Thus it follows that f′(x0) = f for all x0, and in particular also for x0 = 0.
Solution to Exercise 3.2, page 125
Suppose that f′(x0) = L ∈ CL(X, Y). Let M > 0 be such that ||Lh||  M||h||, for all h ∈ X. Let
M||h||, for all h ∈ X. Let  > 0. Then there exists a δ1 > 0 such that whenever x ∈ X satisfies 0 < ||x − x0|| < δ1, we have
> 0. Then there exists a δ1 > 0 such that whenever x ∈ X satisfies 0 < ||x − x0|| < δ1, we have

So if x ∈ X satisfies ||x − x0|| < δ1, then ||f(x) − f(x0) − L(x − x0)|| 
 ||x − x0||.
||x − x0||.
Let 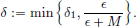 Then for all x ∈ X satisfying ||x − x0|| < δ, we have
Then for all x ∈ X satisfying ||x − x0|| < δ, we have
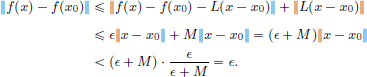
Hence f is continuous at x0.
Solution to Exercise 3.3, page 125
(Rough work: We have for x ∈ C1[0, 1] that

where L : C1[0, 1] → R is the map given by Lh = 2x′0(1)h′(1), h′ ∈ C1[0, 1]. So we make the guess that f′(x0) = L.)
Let us first check that L is a continuous linear transformation. L is linear because:
(L1)For all h1, h2 ∈ C1[0, 1], we have

(L2)For all h ∈ C1 [0, 1] and α ∈ R, we have

Also, L is continuous since for all h ∈ C1[0, 1], we have

So L is a continuous linear transformation. Moreover, for all x ∈ C1[0, 1],

so that 
Given  > 0, set δ =
> 0, set δ =  . Then if x ∈ C1[0, 1] satisfies 0 < ||x − x0||1, ∞ < δ, we have
. Then if x ∈ C1[0, 1] satisfies 0 < ||x − x0||1, ∞ < δ, we have

Solution to Exercise 3.4, page 125
Given  > 0, let
> 0, let  ′ > 0 be such that
′ > 0 be such that  ′||x2 − x1|| <
′||x2 − x1|| <  . Let δ′ > 0 such that whenever 0 < ||x − γ(t0)|| < δ′, we have
. Let δ′ > 0 such that whenever 0 < ||x − γ(t0)|| < δ′, we have

Let δ 0 be such that δ ||x2 − x1|| < δ′. For all t ∈ R satisfying 0 < |t − t0| < δ,
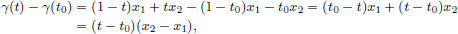
and so ||γ(t) − γ(t0)|| = |t − t0|||x2 − x1||  δ||x2 − x1|| < δ′. Thus for all t ∈ R satisfying 0 < |t − t0| < δ, we have
δ||x2 − x1|| < δ′. Thus for all t ∈ R satisfying 0 < |t − t0| < δ, we have
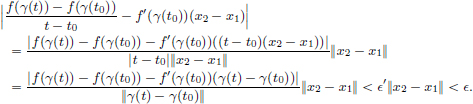
Thus f  γ is differentiable at t0 and
γ is differentiable at t0 and 
Let x1, x2 ∈ X be such that g(X1) ≠ g(X2). With γ the same as above, we have for all t ∈ R that

So g  γ is constant. Thus (g
γ is constant. Thus (g  γ)(1) = g(x2) = g(x1) = (g
γ)(1) = g(x2) = g(x1) = (g  γ)(0), a contradiction. Consequently, g is constant.
γ)(0), a contradiction. Consequently, g is constant.
Solution to Exercise 3.5, page 128
Suppose that f′(x0) = 0. Then for every 
In particular, setting h = x0, we have 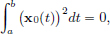 giving x0 = 0 ∈ C[a, b].
giving x0 = 0 ∈ C[a, b].
Vice versa, if x0 = 0, then
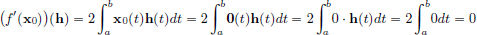
for all h ∈ C[a, b], that is, f′(0) = 0.
Consequently, f′(x0) = 0 if and only if x0 = 0.
So we see that if x∗ is a minimiser, then f′(x∗) = 0, and so from the above x∗ = 0. We remark that 0 is easily seen to be the minimiser because
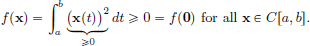
Solution to Exercise 3.6, page 129
If x1, x2 ∈ S, α ∈ (0, 1), then x1, x2 ∈ C1[a, b]. So (1 − α)x1 + αx2 ∈ C1[a, b]. Moreover, as x1(a) = x2(a) = ya and x1b = x2(b) = yb, we also have that
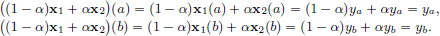
Thus (1 − α)x1 + αx2 ∈ S. Consequently, S is convex.
Solution to Exercise 3.7, page 129
For x1, x2 ∈ X and α ∈ (0, 1) we have by the triangle inequality that

Thus || · || is convex.
Solution to Exercise 3.8, page 129
(If part:) Let x1, x2 ∈ C and α ∈ (0, 1). Then we have that (x1, f(x1) ∈ U(f) and (x2, f(x2)) ∈ U(f). Since U(f) is convex,

Consequently, (1 − α)f(x1) + αf(x2) = y  f(x) = f((1 − α) · x1 + α · x2). Hence f is convex.
f(x) = f((1 − α) · x1 + α · x2). Hence f is convex.
(Only if part:) Let (x1, y1), (x2, y2) ∈ U(f) and α ∈ (0, 1). Then we know that y1  f(x1) and y2
f(x1) and y2  f(x2) and so
f(x2) and so

Consequently,  that is,
that is,
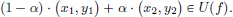
So U(f) is convex.
Solution to Exercise 3.9, page 129
We prove this using induction on n. The result is trivially true when n = 1, and in fact we have equality in this case. Suppose the inequality has been established for some n ∈ N. If x1, ···, xn, xn+1 are n + 1 vectors, and  then
then

and so the claim follows for all n.
Solution to Exercise 3.10, page 130
We have for all x ∈ R
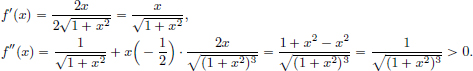
Thus f is convex.
(Alternately, one could note that  is a norm on R2, and so it is convex. Now fixing y = 1, and keeping x variable, we get convexity of
is a norm on R2, and so it is convex. Now fixing y = 1, and keeping x variable, we get convexity of 
Solution to Exercise 3.11, page 132
For x1, x2 ∈ C1[0, 1] and α ∈ (0, 1), we have, using the convexity of function  (Exercise 3.10, page 130), that
(Exercise 3.10, page 130), that
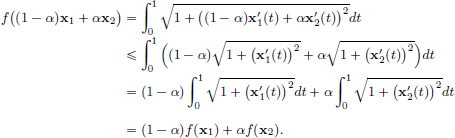
Solution to Exercise 3.12, page 133
(If:) Suppose that x0(t) = 0 for all t ∈ [0, 1]. Then we have that for all h ∈ C[0, 1],

and so f′(x0) = 0.
(Only if:) Now suppose that f′(x0) = 0. Thus for every h ∈ C[0, 1], we have
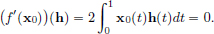
In particular, taking h := x0 ∈ C[0, 1], we obtain 
So 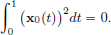 As x0 is continuous on [0, 1], it follows that x0 = 0.
As x0 is continuous on [0, 1], it follows that x0 = 0.
By the necessary condition for x0 to be a minimiser, we have that f′(x0) = 0 and so x0 must be the zero function 0 on [0, 1]. Furthermore, as f is convex and f′(0) = 0, it follows that the zero function is a minimiser. Consequently, there exists a unique solution to the optimisation problem, namely the zero function 0 ∈ C[0, 1]. The conclusion is also obvious from the fact that for all x ∈ C[0, 1],

Solution to Exercise 3.13, page 141
We have 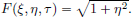 Then
Then 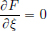 and
and 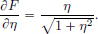
The Euler-Lagrange equation is 
Upon integrating, we obtain 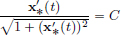 on [a, b] for some constant C.
on [a, b] for some constant C.
Thus  , for all t ∈ [a, b].
, for all t ∈ [a, b].
So A  0, and
0, and  for each t ∈ [a, b]. As
for each t ∈ [a, b]. As  is continuous, we can conclude that
is continuous, we can conclude that  must be either everywhere equal to
must be either everywhere equal to 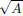 , or everywhere equal to −
, or everywhere equal to −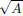 . In either case,
. In either case,  is constant, and so x∗ is given by x∗(t) = αt + β, t ∈ [a, b]. Since x∗(a) = xa and x∗(b) = xb, we have
is constant, and so x∗ is given by x∗(t) = αt + β, t ∈ [a, b]. Since x∗(a) = xa and x∗(b) = xb, we have

and  for all t ∈ [a, b].
for all t ∈ [a, b].
That this x∗ ∈ S is indeed a minimiser can be concluded by noticing that the map x  L(γx) : S → R is convex, thanks to the convexity of
L(γx) : S → R is convex, thanks to the convexity of 
 for all η ∈ R (Exercise 3.10, page 130).
for all η ∈ R (Exercise 3.10, page 130).
(The fact that x∗ is a minimiser, is of course expected geometrically, since the straight line is the curve of shortest length between two points in the Euclidean plane.)
Solution to Exercise 3.14, page 141
We have 
Solution to Exercise 3.15, page 141
With  we have
we have

Then 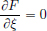 and
and 
The Euler-Lagrange equation is 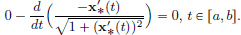
Upon integrating, we obtain  on [a, b] for some constant C.
on [a, b] for some constant C.
Thus 
So A  0, and
0, and  for each t ∈ [a, b]. As
for each t ∈ [a, b]. As  is continuous, we can conclude that
is continuous, we can conclude that  must be either everywhere equal to
must be either everywhere equal to 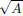 , or everywhere equal to −
, or everywhere equal to −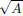 . In either case,
. In either case,  is constant, and so x∗ is given by x∗(t) = αt + β, t ∈ [a, b]. Since x∗(a) = xa and x∗(b) = xb, we have
is constant, and so x∗ is given by x∗(t) = αt + β, t ∈ [a, b]. Since x∗(a) = xa and x∗(b) = xb, we have

and  for all t ∈ [a, b]
for all t ∈ [a, b]
We will now show that this x∗ is a maximiser of x  L(γx) : S → R, that is, it is a minimiser of x
L(γx) : S → R, that is, it is a minimiser of x  −L(γx). Note that the map
−L(γx). Note that the map  is convex because
is convex because
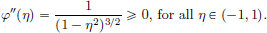
Hence x  −L(γx) : S → R is convex too, and this proves our claim.
−L(γx) : S → R is convex too, and this proves our claim.
Solution to Exercise 3.16, page 142
We have  Thus
Thus

So the Euler-Lagrange equations are

that is,

Solution to Exercise 3.17, page 143
(1)With  we have that
we have that

We have 
So the Euler-Lagrange equation is

We have

Similarly 
Thus the Euler-Lagrange equation becomes (using uxy = uyx)
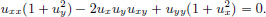
If u = Ax + By + C, then uxx = 0, uxy = 0 and uyy = 0, so that all the three
summands on the left-hand side of the Euler-Lagrange equation vanish, and so we see that the Euler-Lagrange equation is satisfied.
If u = tan–1 (y/x), then we have
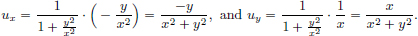
Thus uxx = 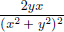 , uxy = uyx =
, uxy = uyx = 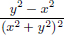 , and uyy =
, and uyy = 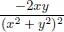 .
.
Hence
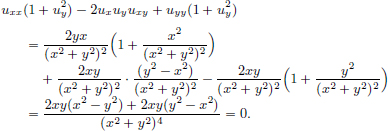
With s := 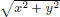 and t = tan–1(y/x) = u, we have tan t =
and t = tan–1(y/x) = u, we have tan t = 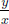 , and so
, and so
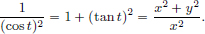
Thus x = 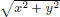 · cos t = s · cos t. Then
· cos t = s · cos t. Then
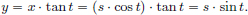
Vice versa, if x = s · cos t, y = s · sin t and u = t, then

and so s = 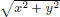 . Also
. Also 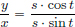 = tan t, and so u = tan–1(y/x) = t.
= tan t, and so u = tan–1(y/x) = t.
Using the Maple command given in the exercise we obtain the following:

(2)If L(X1, X2, U, V1, V2) :=  , then I(u) =
, then I(u) =  .
.
We have 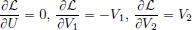 .
.
So the Euler-Lagrange equation is:
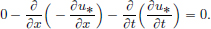
Thus u∗ satisfies the wave equation  = 0.
= 0.
We can check this by direct differentiation that the given u in terms of f satisfies the wave equation. We have

Differentiating again with respect to t, we obtain
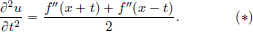
Similarly, by differentiating u with respect to x we obtain

Differentiating again with respect to x, we obtain
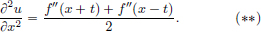
It follows from (∗) and (∗∗) that 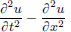 = 0.
= 0.
Let us check that the boundary conditions are satisfied.
Note that u(0, t) =  = 0 since f is odd.
= 0 since f is odd.
Now we would like to check u(1, t) = 0 too.
Using the oddness and 2-periodicity of f, we have

So u(1, t) = 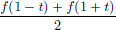 = 0.
= 0.
Finally, we can check if the initial conditions is satisfied.
We have u(x, 0) =  = f(x) for all x.
= f(x) for all x.
Also, from our previous calculation, we have

for all x.
For a fixed t, the graph of f(· –t) is just a shifted version of the graph of f by t units to the right. As t increases, the graph travels to the right, representing a travelling wave, moving to the right with a speed 1. Similarly the graph of f(·+t) with increasing t represents a travelling wave moving to the left with speed 1. The solution of the wave equation is an average of these two travelling waves moving in opposite directions, and the shape of the wave is determined by the initial shape of the string.
We have (suppressing the argument (q, p) everywhere)
Also,

Finally, we will prove the Jacobi Identity. In order to simplify the notation, we will use subscripts to denote partial derivatives, for example Fp will mean  .First we note that
.First we note that
Similarly, by making cyclic substitutions F → G → H above, we obtain
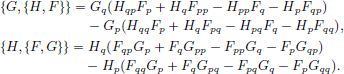
Thanks to the symmetry of the left-hand side of the expression in Jacobi’s Identity in F, G, H, it is enough to show that after collecting all the Fq, Fp terms, their overall coefficients are zero.
The overall coefficient of Fq is

Since Gpq = Gqp and Hpq = Hqp, we see that the above expression is 0.
The overall coefficient of Fp is
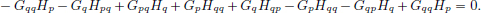
This completes the proof of the Jacobi Identity.
We have {Q, P} =  = 1 · 1 – 0 · 0 = 1.
= 1 · 1 – 0 · 0 = 1.
With x := 1 = (t  1), and y := (t
1), and y := (t  t), 2||x||2∞ + 2||y||2∞ = 2 · 12 + 2 · 12 = 4, while ||x + y||2∞ + ||x – y||2∞ = ||1 + t||2∞ + ||1 – t||2∞ = 22 + 12 = 5. So ||·||∞ does not obey the Parallelogram Law, and hence ||·||∞ cannot be a norm induced by some inner product on C[0, 1].
t), 2||x||2∞ + 2||y||2∞ = 2 · 12 + 2 · 12 = 4, while ||x + y||2∞ + ||x – y||2∞ = ||1 + t||2∞ + ||1 – t||2∞ = 22 + 12 = 5. So ||·||∞ does not obey the Parallelogram Law, and hence ||·||∞ cannot be a norm induced by some inner product on C[0, 1].
Let x, y, z ∈ X. Then

Adding these, we obtain

Geometric interpretation in R2: If x, y, z are the vertices of a triangle ABC, then 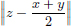 is the length of the median AD (see the picture).
is the length of the median AD (see the picture).
The Appollonius Identity gives AB2 + AC2 =  BC2 + 2AD2.
BC2 + 2AD2.

Let  > 0. Let N1 ∈ N be such that for all n > N1, ||xn – x|| <
> 0. Let N1 ∈ N be such that for all n > N1, ||xn – x|| <  .
.
Let N2 ∈ N be such that for all n > N2, ||yn – y|| < 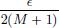 , where the number M :=
, where the number M :=  ||xn|| < ∞ (this exists since (xn)n∈N, being convergent, is bounded).
||xn|| < ∞ (this exists since (xn)n∈N, being convergent, is bounded).
Consequently, for all n > N := max{N1, N2},

Hence (〈xn, yn〉)n∈N is convergent in K, with limit 〈x, y〉.
If the ellipse has major and minor axis lengths as 2a and 2b, respectively, then observe that the perimeter is given by

where the last expression is obtained by rotating the ellipse through 90°, obtaining a new ellipse with the same perimeter.

Using Cauchy-Schwarz Inequality we obtain
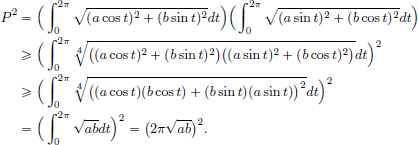
Thus P  2π√ab. Since the areas of the circle and the ellipse are equal, it follows that πr2 = πab, where r denotes the radius of the circle. Hence r = √ab. So we have P
2π√ab. Since the areas of the circle and the ellipse are equal, it follows that πr2 = πab, where r denotes the radius of the circle. Hence r = √ab. So we have P  2π√ab = 2πr, that is, the perimeter P of the ellipse is at least as large as the circumference of the circle.
2π√ab = 2πr, that is, the perimeter P of the ellipse is at least as large as the circumference of the circle.
(IP1)If A ∈ Rm×n, then 〈A, A〉 = tr(A A) =
A) =  aki aki =
aki aki =  a2ki
a2ki  0.
0.
If A ∈ Rm×n and 〈A, A〉 = 0, then  a2ki = 0, and so for all
a2ki = 0, and so for all
k ∈ {1, ···, m} and all i ∈ {1, ···, n}, aki = 0, that is, A = 0.
(IP2)For all A1, A2, B ∈ Rm×n,

For all A, B ∈ Rm×n and α ∈ R,

(IP3)For all A, B ∈ Rm×n,

This is a Hilbert space, since finite-dimensional normed spaces are complete.
Let x, y ∈ X. Then

Also,
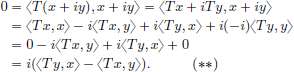
From (∗) and (∗∗) it follows that for all x, y ∈ X, 〈Tx, Ty〉 = 0.
In particular, with y = Tx, we get 〈Tx, Tx〉 = 0, that is, ||Tx||2 = 0.
Hence for all x ∈ X, Tx = 0, that is, T = 0.
We have 〈Tx, x〉 = 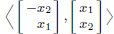 = –x2x1 + x1x2 = 0, for all x =
= –x2x1 + x1x2 = 0, for all x =  ∈ R2.
∈ R2.
There is no contradiction to the previous part since the vector space R2 is a vector space over the real scalars.
R is an equivalence relation on C:
(ER1)If x = (xn)n∈N ∈ C, then  ||xn – xn||X =
||xn – xn||X =  0 = 0, and so (x, x) ∈ R.
0 = 0, and so (x, x) ∈ R.
(ER2)If x = (xn)n∈N, y = (yn)n∈N ∈ C, and (x, y) ∈ R, then  ||xn –yn||X = 0.
||xn –yn||X = 0.
So  ||yn – xn||X =
||yn – xn||X =  |–1| ||xn – yn||X =
|–1| ||xn – yn||X =  ||xn – yn||X = 0.
||xn – yn||X = 0.
Hence (y, x) ∈ R.
(ER3)Let x = (xn)n∈N, y = (yn)n∈N, z = (zn)n∈N be in C, such that (x, y) ∈ R and (y, z) ∈ R. Then  ||xn – yn||X = 0 and
||xn – yn||X = 0 and  ||yn – zn||X = 0.
||yn – zn||X = 0.
As 0  ||xn – zn||X
||xn – zn||X  ||xn – yn||X + ||yn – zn||X , we get
||xn – yn||X + ||yn – zn||X , we get  ||xn – zn||X = 0.
||xn – zn||X = 0.
So (x, z) ∈ R.
Consequently, R is an equivalence relation on C.
 is well-defined:
is well-defined:
If [(xn)n∈N] = [(x′n)n∈N] and [(yn)n∈N] = [(y′n)n∈N], then we wish to show that [(xn + yn)n∈N] = [(x′n + y′n)n∈N]. We have that (xn + yn)n∈N ∈ C, since (xn)n∈N, (yn)n∈N ∈ C and ||xn + yn – (xm + ym)||X  ||xn – xm||X + ||yn – ym||X.
||xn – xm||X + ||yn – ym||X.
Similarly, (x′n + y′n)n∈N ∈ C.
Furthermore, 0  ||(xn + yn) – (x′n + y′n)||X + ||xn + x′n||X + ||yn + y′n)||X, and so
||(xn + yn) – (x′n + y′n)||X + ||xn + x′n||X + ||yn + y′n)||X, and so
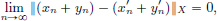
that is, ((xn + yn)n∈N, (x′n + y′n)||n∈N) ∈ R. So [(xn + yn)n∈N] = [(x′n + y′n)||n∈N].
 is well-defined:
is well-defined:
Let α ∈ K and [(xn)n∈N] = [x′n)n∈N]. Since ||αxn – αxm||X = |α|||xn – xm||X, clearly (αxn)n∈N ∈ C. Similarly, (αx′n)n∈N ∈ C. We have

and so ((αxn)n∈N, (αx′n)n∈N) ∈ R. So [(αxn)n∈N] = [(αx′n)n∈N].
 is well-defined:
is well-defined:
Since Cauchy sequences are bounded, given (xn)n∈N, (yn)n∈N in C, we have that Mx := 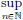 ||xn||X < ∞ and My :=
||xn||X < ∞ and My := 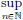 ||yn||X < ∞.
||yn||X < ∞.
Let N be large enough so that if m, n > N, then

Thus for m, n > N,

So (〈xn, yn〉X)n∈N is a Cauchy sequence in K, and as K (= R or C) is complete, it follows that  〈xn, yn〉X exists.
〈xn, yn〉X exists.
Now suppose that [(xn)n∈N] = [(x′n)n∈N] and [(yn)n∈N] = [(y′n)n∈N].
Given  > 0, let N be such that for all n > N,
> 0, let N be such that for all n > N,

where Mx′ = 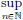 ||x′n||X < ∞. For n > N, we have
||x′n||X < ∞. For n > N, we have

Passing the limit as n → ∞, we obtain 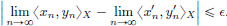
〈·, ·〉 defines an inner product on X:
(IP1)If 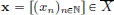 , then
, then  .
.
Let 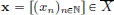 be such that
be such that  = 0.
= 0.
Then  〈xn, xn〉X =
〈xn, xn〉X =  ||xn||2X = 0.
||xn||2X = 0.
(0)n∈N ∈ C and  ||xn – 0||X =
||xn – 0||X =  ||xn||X = 0 (using the above).
||xn||X = 0 (using the above).
Thus [(xn)n∈N] = [(0)n∈N].
(IP2)For all x1, x2, y ∈ X,

For all α ∈ K and x, y ∈ X, we have

(IP3)For all x, y ∈ X, 〈x, y〉X =  .
.

ι is a linear transformation:

ι is injective:
If ι(x) = [(x)n∈N] = [(0)n∈N], then ||x|| =  ||x – 0|| = 0, and so x = 0.
||x – 0|| = 0, and so x = 0.
ι preserves inner products: For x, y ∈ X, 〈ι(x), ι(y)〉X =  〈x, y〉X = 〈x, y〉X.
〈x, y〉X = 〈x, y〉X.
As span{v1} = span{x1} = span{u1}, it follows that v1 = α1u1.
Thus 1 = ||v1|| = |α1|||u1|| = |α1| · 1 = |α1|.
For n > 1, vn ∈ span{v1, ···, vn} = span{x1, ···, xn} = span{u1, ···, un}.
So there are scalars β1, ···, βn–1, αn such that vn = β1u1 + ··· + βn–1un–1 + αnun. We also know that for all k < n, 〈vn, vk〉 = 0. So it follows that 〈vn, v〉 = 0 for all v ∈ span{v1, ···, vn–1} = span{x1, ···, xn–1} = span{u1, ···, un–1}. Thus 〈vn, uk〉 = 0 for all k < n. This gives β1 = ··· = βn–1 = 0, and vn = αnun. Moreover, 1 = ||vn|| = |αn| ||un|| = |αn| · 1 = |αn|.
Let us first note that the derivative of an even monomial t2k is odd, and that of an odd monomial t2k+1 is even. From here it follows that the derivative of a polynomial with only even monomials is a polynomial consisting of only odd monomials, while that of a polynomial with only odd monomials is a polynomial with only even monomials.
By the Binomial Theorem, we see that the polynomial (t2 – 1)n is the sum of even monomials of the form ckt2k, for suitable scalars ck, k = 0, ···, n.
So 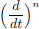 (t2 – 1)n will be a polynomial p with:
(t2 – 1)n will be a polynomial p with:
(1) only even monomials if n is even,
(2) only odd monomials if n is odd.
In the former case, when n is even, p, being the sum of even functions will be even, while in the latter case, p, being the sum of odd functions, will be odd. Thus Pn is even when n is even, and odd if n is odd.
If n is odd, then each of the terms ckt2k–n is an odd polynomial, and hence so is their sum. Consequently, Pn is odd if n is odd.
We have Pn(–1) = (–1)nPn(1) = (–1)n · 1 = (–1)n for all n  0.
0.
With y(t) := (t2 – 1)n, we have y′(t) = n(t2 – 1)n–1 · 2t. So

By differentiating the left-hand side of (∗), we obtain

and by differentiating the right-hand side of (∗), we have

Equating the final expressions from the above calculations, we obtain

Multiplying by 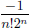 , we get (1 – t2)P″n(t) – 2tP″n(t) + n(n + 1)Pn(t) = 0.
, we get (1 – t2)P″n(t) – 2tP″n(t) + n(n + 1)Pn(t) = 0.
t2 – 1 is zero at ±1. By Rolle’s Theorem, it follows that (d/dt)(t2 – 1) is zero at some t(1) ∈ (–1, 1). But we had seen that (d/dt)(t2 – 1) is also zero at the end points ±1. So by Rolle’s Theorem applied to the function (d/dt)(t2 – 1) on the two intervals [–1, t(1)] and [t(1), 1], we get the existence of points t1(2) ∈ (–1, t(1)) and t2(2) ∈ (t(1), 1), where (d/dt)2(t2 – 1) is zero. Proceeding in this manner, we get the existence of points t1(n), ···, tn(n) ∈ (–1, 1) where (d/dt)n(t2 – 1)n vanishes. So Pn has at least n zeros on (–1, 1). But Pn has degree n, and hence it can have at most n zeros in C. This shows that all the zeros of Pn are real, and all of them lie in the open interval (–1, 1).
The set {eij : 1  i
i  m, 1
m, 1  j
j  n}, where eij is the matrix with 1 in the ith row and jth column, and all other entries 0, is a basis for Rm×n. To see that this basis is in fact orthonormal, observe that the map ι : Rm×n → Rmn given by A = [aij]
n}, where eij is the matrix with 1 in the ith row and jth column, and all other entries 0, is a basis for Rm×n. To see that this basis is in fact orthonormal, observe that the map ι : Rm×n → Rmn given by A = [aij]  (a11, ···, a1n, a21, ···, a2n, ···, am1, ···, amn) (that is, lay out the rows of A next to each other in one long row), is an isomorphism that preserves inner products:
(a11, ···, a1n, a21, ···, a2n, ···, am1, ···, amn) (that is, lay out the rows of A next to each other in one long row), is an isomorphism that preserves inner products:
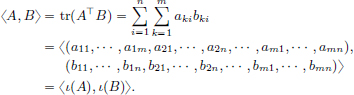
{ι(eij) : 1  i
i  m, 1
m, 1  j
j  n} is orthonormal, and so it follows that the set {eij : 1
n} is orthonormal, and so it follows that the set {eij : 1  i
i  m, 1
m, 1  j
j  n} is orthonormal as well.
n} is orthonormal as well.
(1)We have H0 = ex2e–x2 = 1. For n  0,
0,

Thus if Hn is a polynomial, then 2xHn, H′n are polynomials too, and so is Hn+1 = 2xHn – H′n. Since H0 = 1 is a nonzero polynomial of degree 0, it follows by induction on n that each Hn, n  0 is a polynomial. Moreover, if Hn has degree d, and its leading term is cdxd, then H′n has degree d – 1, while 2xHn has degree d + 1 with the leading term 2cdxd+1. Consequently, the recurrence relation together with H0 = 1 also reveals that Hn has the leading term 2nxn, and in particular has degree n.
0 is a polynomial. Moreover, if Hn has degree d, and its leading term is cdxd, then H′n has degree d – 1, while 2xHn has degree d + 1 with the leading term 2cdxd+1. Consequently, the recurrence relation together with H0 = 1 also reveals that Hn has the leading term 2nxn, and in particular has degree n.
Using the recursion relation, we get H1 = 2x, H2 = 4x2 – 2, H3 = 8x3 – 12x.
(2)Let m < n. Then we have
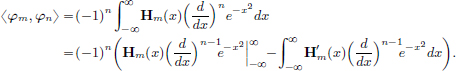
As (d/dx)n–1e–x2 is a sum of terms of the form ckxke–x2, and because Hm is a polynomial, it follows that the first summand in the right-hand side is 0.
So we have 〈φm, φn〉 = (–1)n+1  .
.
We can continue this process of integration by parts, until we arrive at

But as Hm has degree m < n, (d/dx)n Hm = 0, so that 〈φm, φn〉 = 0.
The case m > n also follows from here, since the inner product is conjugate symmetric. Finally,

(The last equality can be justified as follows. With I := 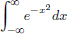 , we have
, we have

So I = 
(3)For n  0, we have
0, we have

(4)First let us note that if n  1, then we have
1, then we have

Hence for n  1,
1,
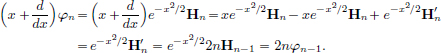
(5)We have for all φ

Hence for all n  0,
0,
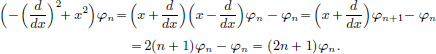
(6)We have  and
and  .
.
From the previous part, we have (–(d/dx)2 + x2)φn = (2n + 1)φn, giving

We have

In Schrödinger’s equation, a2 =  , and so
, and so 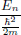 = a(2n + 1).
= a(2n + 1).
So En =  , for n
, for n  0.
0.
Since  diverges,
diverges,  does not converge absolutely.
does not converge absolutely.
If sn is the nth partial sum of  , then for n > m, we have
, then for n > m, we have

and this can be made as small as we please since  .
.
Hence (sn)n∈N is Cauchy in H, and since H is a Hilbert space, it converges.
For all N ∈ N, we have

Thus 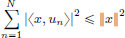 , and as N was arbitrary,
, and as N was arbitrary,  .
.
Let y ∈ Y ∩ Y⊥. As y ∈ Y⊥, we know that for all y′ ∈ Y , 〈y, y′〉 = 0. Taking y′ := y ∈ Y, we obtain 0 = 〈y, y′〉 = 〈y, y〉 = ||y||2, and so ||y|| = 0, giving y = 0. So Y ∩ Y⊥ ⊂ {0}. Also, since Y, Y⊥ are subspaces, it follows that each contains the zero vector 0. So Y ∩ Y⊥ = {0}.
(1)If y ∈ Y, then for each x ∈ Y⊥, 〈y, x〉 = 〈x, y〉∗ = 0, and so y ∈ (Y⊥)⊥. Thus Y ⊂ (Y⊥)⊥.
(2)Let x ∈ Z⊥. Then 〈x, z〉 = 0 for all z ∈ Z. As Y ⊂ Z, we also have 〈x, y〉 = 0 in particular for all y ∈ Y. Hence x ∈ Y⊥. This shows that Z⊥ ⊂ Y⊥.
(3)As Y ⊂ Y, it follows from part (2) that  .
.
Now let x ∈ Y⊥. Then 〈x, y〉 = 0 for all y ∈ Y.
If y′ ∈ Y, then there exists a sequence (yn)n∈N in Y such that  yn = y′. Thus 〈x, y′〉 =
yn = y′. Thus 〈x, y′〉 =  = 0.
= 0.
Hence  , showing that
, showing that  as well.
as well.
(4)Suppose that x ∈ Y⊥.
As Y is dense in X, there is a sequence (yn)n∈N in Y converging to x in X. Thus 〈x, x〉 =  〈x, yn〉 =
〈x, yn〉 =  0 = 0.
0 = 0.
(5)Suppose x = (xn)n∈N ∈ 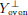 . Since e2n ∈ Yeven for each N, x2n = 〈x, e2n〉 = 0. Hence the subspace
. Since e2n ∈ Yeven for each N, x2n = 〈x, e2n〉 = 0. Hence the subspace  ⊂ Yodd, where Yodd denotes the subspace of ℓ2 all sequences whose evenly indexed terms are 0.
⊂ Yodd, where Yodd denotes the subspace of ℓ2 all sequences whose evenly indexed terms are 0.
Vice versa, if x ∈ Yodd, it is clear that for all y ∈ Yeven, 〈x, y〉 = 0. Thus Yodd ⊂  .
.
Consequently,  = Yodd.
= Yodd.
Similarly,  = Yeven. And so,
= Yeven. And so,  .
.
(6)We know that c00 is dense in ℓ2. (Just truncate the series to the desired accuracy to get a finitely supported approximation!)
So  . But then
. But then 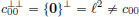 .
.
Let  .
.
Then E(m, b) =  .
.
Thus the problem of finding the least square regression line is:

It follows from Theorem 4.5, page 174, that a minimiser Y∗ is given by
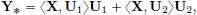
where {U1, U2} is any orthonormal basis for the subspace Y := span{Y1, Y2} of Rn with the usual Euclidean inner product. By the Gram-Schmidt Orthonormalisation Procedure, U1 =  , and U2 =
, and U2 =  .
.

For the given data, using the above formulae, we obtain m = –0.3184 million tonnes coal per °C, and b = 10.4667 million tonnes of coal. The y-intercept is b = 10.4667 million tonnes of coal, and this is the inland energy consumption when the mean temperature is 0°C (that is when it is freezing!). The x-intercept is 10.4667/0.3184 = 32.8728, which is the mean temperature when the inland consumption is 0 (that is, no heating required). The slope is m = –0.3184 million tonnes of coal per °C. Thus for each °C drop in temperature, the inland energy consumption increases by 0.3184 million tonnes of coal. Finally, the forecast of the energy consumption for a month with mean temperature 9°C is given by y = mx + b = (–0.3184)(9) + 10.4667 = 7.6011 million tonnes of coal.
Let C := L2+(R). Then C is convex. Thus C is convex too. We will show that g∗ := max{f, 0} ∈ L2+(R) = C ⊂ C satisfies: for all g ∈ C, 〈f – g∗, g – g∗〉  0.
0.
We have f = max{f, 0} + min{f, 0}. So f – g∗ = min{f, 0}. Also,
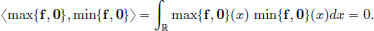
Hence we obtain for all g ∈ C that

So for all g ∈ C, ||f – g∗||  ||f – g||. In particular, for all g ∈ L2+(R) = C ⊂ C, we also have ||f – g∗||
||f – g||. In particular, for all g ∈ L2+(R) = C ⊂ C, we also have ||f – g∗||  ||f – g||.
||f – g||.
We’d seen in Exercise 4.17, page 173, that  . So
. So  , where the last equality follows from Corollary 4.1, page 182, since Y is closed.
, where the last equality follows from Corollary 4.1, page 182, since Y is closed.
For all f ∈ L2(R), it is easy to check that fe := (f +  )/2 is even, and fo := (f –
)/2 is even, and fo := (f –  )/2 is odd. Thus for all g ∈ Y, we have
)/2 is odd. Thus for all g ∈ Y, we have

Thus, by Theorem 4.7, page 180, PYf = fe for all f ∈ L2(R).
By Theorem 4.8, page 180, we have

PY⊥ = I – PY, and so for all f ∈ L2(R), PY⊥f = f –  .
.
We have f = If = PYf + PY⊥f =  .
.
Moreover, by Theorem 4.8, this decomposition is unique.
Y = ker(I – S), and so Y is a closed subspace of H.
For all x ∈ H,  .
.
So  for all x ∈ H. Moreover, for all y ∈ Y, we have
for all x ∈ H. Moreover, for all y ∈ Y, we have

Thus, by Theorem 4.7, page 180, PYx =  for all x ∈ H.
for all x ∈ H.
By Theorem 4.8, page 180, we have

Thus Z⊥ = (Y⊥)⊥ = Y.
PY⊥ = I – PY, and so for all x ∈ H, PY⊥x = x – 
Consider the map  , where
, where  is the indicator function of
is the indicator function of  .
.
As  < ∞, Mf ∈ L2(R).
< ∞, Mf ∈ L2(R).
It is also easy to see that M is linear. The above inequality then establishes that M ∈ CL(L2(R)). We have

Thus YA is closed.
For f ∈ L2(R), 1Af ∈ YA, and moreover, for any g ∈ YA,

Thus PAf = 1Af for all f ∈ L2(R).
Suppose that D⊥ = {0}. Then D = (D⊥)⊥ = {0}⊥ = H. So D is dense in H.
Now suppose that D is dense in H. Then D = H. Thus D⊥ = (D)⊥ = H⊥ = {0}.
Let x ∈ C[–1, 1] and  > 0. By Weierstrass’s Approximation Theorem (Exercise 1.26, page 22), there is a polynomial p ∈ C[–1, 1] such that ||x – p||∞ <
> 0. By Weierstrass’s Approximation Theorem (Exercise 1.26, page 22), there is a polynomial p ∈ C[–1, 1] such that ||x – p||∞ <  .
.
Then 
Hence ||x – p||2 <  . Consequently the polynomials are dense in C[–1, 1] (with the usual inner product).
. Consequently the polynomials are dense in C[–1, 1] (with the usual inner product).

Moreover ι is continuous because ||ι(x)||2 =  for all x ∈ H.
for all x ∈ H.
If x ∈ H is such that ι(x) “ 0, then ||x|| = ||ι(x)|| = 0, and so x = 0.
Hence ι is injective.
If (cn)n∈N ∈ ℓ2, then x := 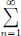 cnun ∈ H, and for all k ∈ N,
cnun ∈ H, and for all k ∈ N,

So ι(x) = (cn)n∈N, showing that ι is surjective too.
As ι ∈ CL(H, ℓ2) is a bijection, it has a continuous inverse ι–1 ∈ CL(ℓ2, H) (by Corollary 2.4 on page 96). Moreover, ||ι(x)|| = ||x|| for all x ∈ H, and so ι is an isometry.
Let x ∈ C[0, 1] be the function t  t.
t.
For n ≠ 0, we have 〈x, Tn〉 =  , using integration by parts.
, using integration by parts.
Also 〈x, T0〉 = 1/2. By Parseval’s Identity,
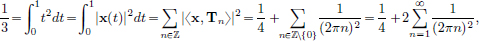
which yields 
Let [(xn)n∈N] ∈ X. Consider the sequence (xn)n∈N in X. Since (xn)n∈N ∈ C, given any  > 0, there exists an N ∈ N such that for all m, n > N, ||xn – xm|| <
> 0, there exists an N ∈ N such that for all m, n > N, ||xn – xm|| <  . Consequently, for all m > N, ||ι(xm) – [(xn)n∈N]||X =
. Consequently, for all m > N, ||ι(xm) – [(xn)n∈N]||X =  ||xm – xn||
||xm – xn|| 
 .
.
Hence  ι(xn) = [(xn)n∈N].
ι(xn) = [(xn)n∈N].
We have

with equality if and only if  .
.
Thus the curve enclosing the maximum area is given by

with 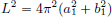 .
.
Let α ∈ [0, 2π) be such that cos α = 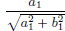 and sin α =
and sin α =  . Then
. Then
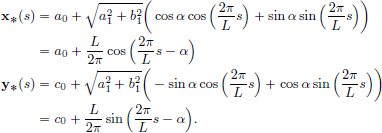
Hence (x∗(s) – a0)2 + (y∗(s) – c0)2 =  .
.
Consequently, s  (x∗(s), y∗(s)) : [0, L] → R2 is the parametric representation of a circle with centre at (a0, c0) ∈ R2 and radius equal to
(x∗(s), y∗(s)) : [0, L] → R2 is the parametric representation of a circle with centre at (a0, c0) ∈ R2 and radius equal to  .
.
(1)Call un the nth vector in the list. If {un : n ∈ N} were an orthonormal basis, then

a contradiction. So the given set is not an orthonormal basis.
(2)Let us call the evenly indexed vectors as vn, and the oddly indexed ones as wn. Then clearly 〈vi, vj〉 = 〈wi, wj〉 = 〈vi, wj〉 = 0 whenever i ≠ j, since there are no overlapping nonzero terms. Also 〈vi, wi〉 = 0.
Finally ||vi|| = ||wi|| = 1. This shows that the given set B is orthonormal. In order to show density, we note that 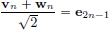 and
and  . Thus span B = span{en : n ∈ N}, and the latter is dense in ℓ2.
. Thus span B = span{en : n ∈ N}, and the latter is dense in ℓ2.
If X is a real vector space, then let KQ := Q, while if X is a complex vector space, then let KQ := Q + iQ. Set

Then D is countable. Let x ∈ X, and  > 0.
> 0.
Then there exists an N such that 
Let cn ∈ KQ, n = 1, ···, N, be such that  .
.
Then with y :=  cnun ∈ B, we have
cnun ∈ B, we have
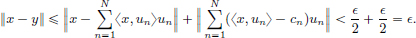
Thus X is separable.
We have for λ ≠ μ that

On the other hand, ||eiλx||2 = 1. Thus

Hence 
Suppose now that X is separable, with a dense subset D = {d1, d2, d3, ···}. Then for each λ ∈ R, there exists a dλ ∈ D such that ||eiλx – dλ|| < 1/√2.
This gives us the existence6 of a map λ  dλ : R → D.
dλ : R → D.
This map is injective since if λ ≠ μ, then
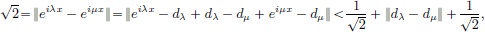
giving ||dλ − dμ|| > 0, and in particular dλ ≠ dμ.
But this is absurd, since R is uncountable, while D is countable!
So 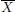 is not separable.
is not separable.
Solution to Exercise 4.33, page 189
For n ∈ N, set 
If Un has more than n − 1 elements, then for any distinct ui1, · · · , uin ∈ Un,

(where the former inequality is by virtue of the fact that the uik ’s belong to Un, and the latter is Bessel’s Inequality). So we obtain ||x||2 < ||x||2, which is absurd. Thus Un has at most n − 1 elements. Hence each Un is finite. But

and as each Un is finite, their union U is at most countable.
Consequently, 〈x, ui〉 is nonzero for at most a countable number of the ui ’s.
Solution to Exercise 4.34, page 190
(1)We have for all x ∈ H that |φy(x)| = |〈x, y〉|  ||x|| ||y||, and so ||φy||
||x|| ||y||, and so ||φy||  ||y||.
||y||.
If y = 0, then ||φy||  ||y|| = 0, and so ||φy|| = 0 = ||y||.
||y|| = 0, and so ||φy|| = 0 = ||y||.
If y ≠ 0, then define z =  , and observe that ||z|| = 1, so that
, and observe that ||z|| = 1, so that

Hence it follows that ||φy|| = ||y||.
(2)Let y ∈ H\{0}. Then for x ∈ H,
and so φiy = −iφy.
Also ||φy|| = ||y|| ≠ 0, so that φy ≠ 0, the zero linear functional.
If the map η  φη : H → CL(H, C) were linear, then in particular, we would have φiy = iφy, and from the above, we would then get iφy = −iφy, giving φy = 0, which is absurd.
φη : H → CL(H, C) were linear, then in particular, we would have φiy = iφy, and from the above, we would then get iφy = −iφy, giving φy = 0, which is absurd.
Solution to Exercise 4.35, page 195
We will show that Y := ran P = ker(I − P), and since the kernel of the continuous linear transformation I − P is closed, it follows that Y is closed.
That ran P = ker(I − P): If y ∈ ran P, then y = Px for some x ∈ H. Then
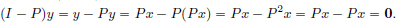
So y ∈ ker(I − P). Hence ran P ⊂ ker(I − P).
On the other hand, if y ∈ ker(I − P), then (I − P)y = 0 and so y = Py ∈ ran P. Thus ker(I − P) ⊂ ran P as well.
It remains to show that P = PY. We will use (ran P)⊥ = ker(P∗) = ker P, where the last equality follows thanks to the self-adjointness of P. Let x ∈ H. Then x = PY x + PY ⊥ x. But PY ⊥ x ∈ Y⊥ = ker P, and so

As PY x ∈ Y = ran P, PY x = Px1 for some x1 ∈ H.
Thus P (PY x) = P (Px1) = P2 x1 = Px1 = PY x. Hence Px = P (PY x) = PY x.
Solution to Exercise 4.36, page 195

and so T1 is self-adjoint, while T2 is skew-adjoint.
Moreover, 
In order to show uniqueness, suppose that T′1, T′2 are self-adjoint and skew-adjoint respectively such that T = T′1 + T′2. Then T1 + T2 = T′1 + T′2, and so we obtain T1 − T′1 = T′2 − T2. As the left-hand side is self-adjoint, and the right-hand side is skew-adjoint, both sides must be zero. (Indeed, if S := T1 − T′1 = T′2 − T2 is the common value, then S = S∗ = −S, and so 2S = 0, that is, S = 0.)
Solution to Exercise 4.37, page 195
 . Define T : ℓ2 → ℓ2 by Tk =
. Define T : ℓ2 → ℓ2 by Tk =  .
.
Then T is well-defined and T ∈ CL(ℓ2). We will show that Λ∗ = T.
For all h = (hn)n∈N and k = (kn)n∈N in ℓ2, we have
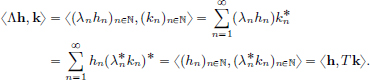
Thus Λ∗ = T.
Solution to Exercise 4.38, page 195
We’ll show that I∗ is given by 
I∗ ∈ CL(L2 [0, 1)] by Example 2.10 (page 70), with 
For h, k ∈ L2 [0, 1], we have
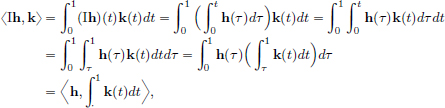
and so I∗ ∈ CL(L2 [0, 1]) is given by 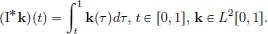
Solution to Exercise 4.39, page 195
T*A = TA∗, where 
Thus T∗A is clockwise rotation through an angle θ in the plane.
Solution to Exercise 4.40, page 196
For x ∈ H, we have 
(Note that x′ ∈ Y⊥n because 〈x′, ui〉 = 0 for all i = 1, · · · ,n.)
So  for all x ∈ H. For all x ∈ H, we have
for all x ∈ H. For all x ∈ H, we have
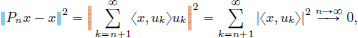
since 
Solution to Exercise 4.41, page 196
(1)If B′ = {u′n: n ∈ N} is another orthonormal basis, then

On the other hand, we also have
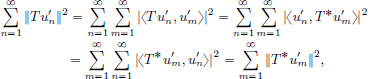
and so 
(2)We will verify simultaneously the norm and subspace axioms:
(N1/S3) For all T ∈ S2 (H) that 
Now let T ∈ S2 (H) and ||T||HS = 0. Then 
So Tun = 0 for all n. But then for all x ∈ H, we have

Consequently T = 0.
Clearly 0 ∈ S2 (H) since ||0||HS = 0 < ∞.
(N2/S2) For all T ∈ S2 (H) and α ∈ K, we have
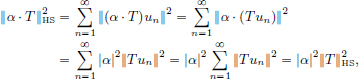
and so ||α · T||HS = |α| ||T||HS.
Note that we’ve also shown for all T ∈ S2 (H), α ∈ K, that α · T ∈ S2 (H).
(N3/S1) Finally, if T1, T2 ∈ S2 (H), then we have
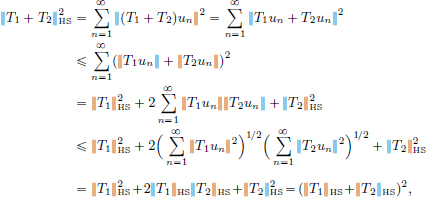
and so ||T1 + T2||HS  ||T1||HS + ||T2||HS.
||T1||HS + ||T2||HS.
Also, this shows that for all T1, T2 ∈ S2 (H), T1 + T2 ∈ S2(H).

and so ||T || = ||T∗||  ||T||HS.
||T||HS.
Solution to Exercise 4.42, page 197
As CL(H) is an algebra, Λ(T) ∈ CL(H). We verify linearity:
(L1) For T1, T2 ∈ CL(H),
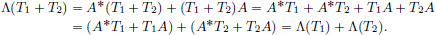
(L2) Λ(αT) = A∗ (αT)+(αT)A = α(A∗ T + T A) = αΛT, T ∈ CL(H), α ∈ K.
Continuity: For T ∈ CL(H),

and so Λ ∈ CL(CL(H)).
If T ∈ CL(H) is such that T = T∗, then
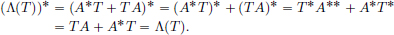
So Λ(T) is self-adjoint.
Solution to Exercise 4.43, page 197
Let (Tn)n∈N be a sequence of self-adjoint operators in CL(H) that converges to T ∈ CL(H). We’d like to show that for all x, y ∈ H, 〈T x, y〉 = 〈x, Ty〉. As we have ||Tnx − T x||  ||Tn − T || ||x||, it follows that (Tnx)n∈N converges to Tx, and similarly, (Tny)n∈N converges to Ty. Thus
||Tn − T || ||x||, it follows that (Tnx)n∈N converges to Tx, and similarly, (Tny)n∈N converges to Ty. Thus

Solution to Exercise 4.44, page 197
Let μ ∈ ρ(T). Then there is an S ∈ CL(H) such that S(μI − T) = I = (μI − T)S. Taking adjoints, we obtain
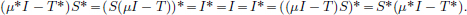
Thus μ∗ I − T∗ is invertible in CL(H), and so μ∗ ∈ ρ(T∗).
So we have proved that  for all T ∈ CL(H).
for all T ∈ CL(H).
Applying this to T∗ instead of T gives:

Consequently for all T ∈ CL(H), μ ∈ ρ(T) if and only if μ∗ ∈ ρ(T∗).
We had seen that R = L∗ and that σ(L) = {z ∈ C : |z|  1}.
1}.
From the above, we obtain σ(R) = C\ρ(R) = C\(ρ(L))∗ = C\ρ(L) = σ(L).
Consequently the spectrum of R is the same as that of L, namely the closed unit
disc {z ∈ C : |z| 1} in the complex plane.
1} in the complex plane.
Solution to Exercise 4.45, page 197
We have for λ ∉ {0, 1},
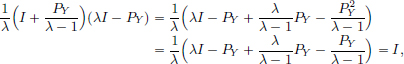
and similarly 
The previous part shows that σ(PY) ⊂ {0, 1}.
We now show that both 0 and 1 are eigenvalues, so that σ(PY) = σp(PY) = {0, 1}.
As Y is a proper subspace, Y ≠ {0}. So there exist nonzero vectors y in Y, and all of these are eigenvectors of PY with eigenvalue 1: PY y = y = 1 · y.
Also, as Y is a proper subspace, Y ≠ H.
If Y⊥ = {0}, then we have that Y = (Y⊥ qK = {0}⊥ = H, a contradiction.
Thus Y⊥ ≠ {0}. But this means that there exist nonzero vectors x in Y⊥.
All of these are eigenvectors of PY with eigenvalue 0, since PY x = 0 = 0 · x.
Solution to Exercise 4.46, page 197
Let λ ∈ σp (U) with eigenvector v ≠ 0.
Then Uv = λv, and so |λ|2 ||v||2 = 〈λv, λv〉 = 〈Uv, Uv〉 = 〈U* Uv, v〉 = 〈Ivv〉 = ||v||2.
Thus |λ| = 1, that is, λ lies on the unit circle with centre 0 in the complex plane.
If v1, v2 ∈ H\{0} are eigenvectors of U corresponding to distinct eigenvalues λ1, λ2, then we have

and so 〈v1, v2〉 = 0.
Solution to Exercise 4.47, page 199
The spectrum of T is real, and hence T + iI is invertible in CL(H). Since (T + iI)(T − iI) = T2 + I = (T − iI)(T + iI), it follows by pre- and post-multiplying with (T + iI)−1 that (T − iI)(T + iI)−1 = (T + iI)−1(T − iI) =: U. Hence we have

So

Thus U is unitary. We have
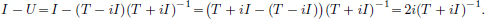
Hence I − U is invertible in CL(H) with inverse 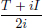 . Similarly,
. Similarly,

So 
Solution to Exercise 4.48, page 199
(1)Suppose that PY  PZ. If y ∈ Y, then
PZ. If y ∈ Y, then
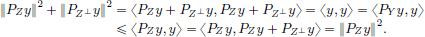
So PZ⊥ y = 0, giving y = PZ y + PZ⊥ y = PZ y + 0 = PZ y ∈ Z. Thus Y ⊂ Z.
(2)Now let Y ⊂ Z and x ∈ H. We have PZ x = PY x + (PZ x − PY x).
We first show that PZx − PYx is perpendicular to PYx.
As x = PY x + PY⊥x = PZ x + PZ⊥x, we have PZ x − PY x = PY⊥x − PZ⊥x.
So 〈PY x, PZ x − PY x〉 = 〈PY x, PY⊥x − PZ⊥x〉 =  = 0.
= 0.
Hence

Consequently, PY  PZ.
PZ.
Solution to Exercise 4.49, page 204
(1)By the Fundamental Theorem of Calculus, 
So 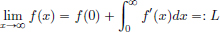 .
.
As f (x)  0 for all x, we must have that L
0 for all x, we must have that L  0. Suppose that L > 0.
0. Suppose that L > 0.
Then there exists an R > 0 such that for all x > R, L −f (x)  |f (x) − L| <
|f (x) − L| <  , and in particular, f (x) >
, and in particular, f (x) >  for all x > R. Hence for all x > R,
for all x > R. Hence for all x > R,

which is absurd. Hence L = 0.
(2)We apply part (1) with f (x) := |Ψ(x)|2.
We note that f′ = (|Ψ|2)′ = (ΨΨ*)′ = Ψ′Ψ* + Ψ(Ψ′)*, and so |f′|  2||Ψ|| ||Ψ′||.
2||Ψ|| ||Ψ′||.
Thus 
So 
To show that  , we apply the above to x
, we apply the above to x  Ψ(−x), and note that if Ψ, Ψ′ ∈ L2 (R), then so do Ψ(−·), (Ψ(−·))′ = −Ψ′(−·).
Ψ(−x), and note that if Ψ, Ψ′ ∈ L2 (R), then so do Ψ(−·), (Ψ(−·))′ = −Ψ′(−·).
Solution to Exercise 4.50, page 205
We have for self-adjoint A, B that
[A, B]∗ = (AB − BA)∗ = B∗ A∗ − A∗B∗ = BA − AB = −(AB − BA) = −[A, B].
Solution to Exercise 4.51, page 205
We have

Similarly, Hence
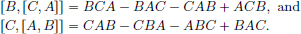
Hence
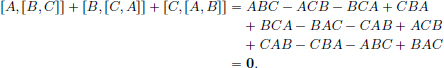
Solution to Exercise 4.52, page 205
If n = 1, then [Q, P] = −[P, Q] = −(−i I) = i
I) = i 1Q1−1, and so the claim is true. If [Qn, P] = i
1Q1−1, and so the claim is true. If [Qn, P] = i nQn−1 for some n ∈ N, then we have
nQn−1 for some n ∈ N, then we have
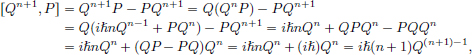
and so the claim follows for all n ∈ N by induction.
Solution to Exercise 4.53, page 207
We have in the classical case that

Thus {Q2, P2} = 4QP.
In the quantum mechanical case, we have, using Exercise 4.52, page 205, that

Thus  (since otherwise QP = PQ, which is false since [Q, P] = i
(since otherwise QP = PQ, which is false since [Q, P] = i I ≠ 0).
I ≠ 0).
QP is not self-adjoint, since if it were self-adjoint, then for all compactly supported Ψ and Φ, we would have

which would give i Φ = [Q, P] Φ = 0, which is clearly false for nonzero Φ! On the other hand, for all Ψ and Φ, we have
Φ = [Q, P] Φ = 0, which is clearly false for nonzero Φ! On the other hand, for all Ψ and Φ, we have

Solution to Exercise 4.54, page 207
We have

and so t  ||ψ(t)||2 is constant, giving ||ψ(t)||2 = ||ψ(0)||2 = 1.
||ψ(t)||2 is constant, giving ||ψ(t)||2 = ||ψ(0)||2 = 1.
Solution to Exercise 4.55, page 207
As V ≡ 0 for x ∈ (0, π), we have  , that is,
, that is, 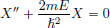 .
.
Depending on the sign of E, the solution is given by

If E = 0, then the conditions X(0) = X(π) = 0 give A = B = 0. So X ≡ 0.
If E < 0, then the conditions X(0) = X(π) imply that A = B = 0 so that X ≡ 0.
So only the case E > 0 remains. The condition X(0) = 0 gives A = 0.
The condition X(π) = 0 implies B sin 
As we want nontrivial solutions, we know B ≠ 0 (otherwise X ≡ 0).
So sin  , giving
, giving 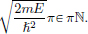
Thus  (discrete/“quantised” energy levels!).
(discrete/“quantised” energy levels!).
We have |Ψ(x, t)| = |X(x)||T (t)| = |X(x)| · |C| = |C| · |B| · | sin(nx)|.
The plots of |Ψ|2 = constant · sin(nx))2 when n = 1, 2 are shown below.

When n = 1, the probability is

When n = 2, the probability is

Solutions to the exercises from Chapter 5
Solution to Exercise 5.1, page 215
(1)Tm is linear:
(L1) For all x1, x2 ∈ H,

(L2) For all x ∈ H and α ∈ K,

So Tm is a linear transformation. Next we prove continuity: for all x ∈ H,

Conclusion: Tm ∈ CL(H).
For x ∈ H we have

(2)As  , we have
, we have 
Thus (Tm)m∈N converges to T in CL(H). Since the range of Tm is contained in the span of Tu1, · · ·, Tum, it follows that Tm has finite rank, and so Tm is compact. As T is the limit in CL(H) of a sequence of compact operators, it follows that T is compact.
Solution to Exercise 5.2, page 216
(1)(L1) For x1, x2 ∈ H, we have
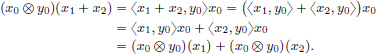
(L2) For α ∈ K and x ∈ H, we have

Continuity: For x ∈ H, we have
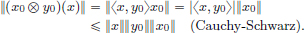
So x0  y0 ∈ CL(H), and ||x0
y0 ∈ CL(H), and ||x0  y0||
y0||  ||x0 || ||y0||.
||x0 || ||y0||.
(2)As ran(x0  y0) ⊂ span{x0}, we have that x0
y0) ⊂ span{x0}, we have that x0  y0 has finite rank, and so it is compact.
y0 has finite rank, and so it is compact.
(3)For all x ∈ H,

Since this is true for all x ∈ H, we conclude that A(x0 y0)B = (Ax0)
y0)B = (Ax0) (B∗ y0).
(B∗ y0).
Solution to Exercise 5.3, page 217
(1)Let H = ℓ2, and T be diagonal with 2 × 2 nilpotent blocks 
More explicitly, T (a1, a2, a3, a4, a5, a6, · · ·) = (a2, 0, a4, 0, a6, 0, · · ·), for all (an)n∈N ∈ ℓ2. Thus T ∈ CL(ℓ2). Also, T2 = 0 is compact.
But if we take the bounded sequence (e2n)n∈N, then (Te2n)n∈N = (e2n−1)n∈N, and this has no convergent subsequence. Hence T is not compact.
(2)Suppose that (xn)n∈N is a bounded sequence in H, and ||xn||  M for all n. Since T2 is compact, (T2xn)n∈N has a convergent subsequence, say (T2 xnk)k∈N. We will show that (T xnk)k∈N is also convergent, by showing that it is Cauchy. We have for j, k that
M for all n. Since T2 is compact, (T2xn)n∈N has a convergent subsequence, say (T2 xnk)k∈N. We will show that (T xnk)k∈N is also convergent, by showing that it is Cauchy. We have for j, k that

and so (T xnk)k∈N is Cauchy. As H is a Hilbert space, it follows that (T xnk)k∈N is convergent. Hence T is compact.
Solution to Exercise 5.4, page 217
(1)True.
Neither I nor −I is compact, but their sum is 0, which is compact.
(3)True.
(4)False.
See the example in the solution to Exercise 5.3, part (1), page 217.
Alternately, we could take two diagonal operators on ℓ2 corresponding to the sequences (1, 0, 1, 0, 1, 0, · · ·) and (0, 1, 0, 1, 0, 1, · · ·).
Solution to Exercise 5.5, page 217
If T ∈ K(H), then as A∗ ∈ CL(H), we have A∗T ∈ K(H). Also, TA ∈ K(H) because T ∈ K(H) and A ∈ CL(H). Since A∗T and TA are in K(H), also their sum A∗T + TA ∈ K(H), that is, Λ(T) ∈ K(H). Thus K(H) is Λ-invariant.
Solution to Exercise 5.6, page 226
We have ker T = {0}. So ran T = (ker T∗)⊥ = (ker T)⊥ = {0}⊥ = H.
So T has infinite rank. Let x ∈ H = ranT, and  > 0. Then there exists a y ∈ ran T, such that ||x − y|| <
> 0. Then there exists a y ∈ ran T, such that ||x − y|| <  /2.
/2.
As y ∈ ran T, we have y = T x′, for some x′ ∈ H, and 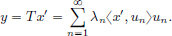
So there exists an N Such that with

we have ||y − z|| <  /2. Consequently, ||x − z||
/2. Consequently, ||x − z||  ||x − y|| + ||y − z|| <
||x − y|| + ||y − z|| <  /2 +
/2 +  /2 =
/2 =  , and so span{un : n ∈ N} is dense in H. Since {un : n ∈ N} is also an orthonormal set, it follows that it is an orthonormal basis for H.
, and so span{un : n ∈ N} is dense in H. Since {un : n ∈ N} is also an orthonormal set, it follows that it is an orthonormal basis for H.
Solution to Exercise 5.7, page 226
We note that each eigenvalue λ of T is nonnegative because if u is a corresponding unit-norm eigenvector, then λ = λ · 1 = λ〈u, u〉 = 〈T u, u〉  0. By the spectral theorem, we know that there exists a sequence of orthonormal eigenvectors u1, u2, u3, · · · of T with corresponding eigenvalues λ1
0. By the spectral theorem, we know that there exists a sequence of orthonormal eigenvectors u1, u2, u3, · · · of T with corresponding eigenvalues λ1  λ2
λ2  λ3
λ3  · · ·
· · ·  0.
0.
We will show that for all x ∈ H,  converges in H.
converges in H.
For N > M, we have,

In the above, we have used Bessel’s Inequality to get the last inequality.
Hence  is Cauchy in H. As H is a Hilbert space,
is Cauchy in H. As H is a Hilbert space,

converges in H. Consequently  x is well-defined for all x ∈ H.
x is well-defined for all x ∈ H.
Also, it is easy to see that  is a linear transformation.
is a linear transformation.
Continuity: For all N ∈ N,

Passing the limit N → ∞, we obtain || x||2
x||2  λ1 ||x||2, and so
λ1 ||x||2, and so  ∈ CL(H).
∈ CL(H).
We have for all x ∈ H that

So ( )2 = T.
)2 = T.
Solutions to the exercises from Chapter 6
Solution to Exercise 6.1, page 232
(1)Since 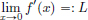 exists, given an
exists, given an  > 0, there exists a δ > 0 such that
> 0, there exists a δ > 0 such that
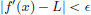
whenever 0 < |h| < δ. Consider the interval [0, h] for some h which satisfies 0 < h < δ. Since f is differentiable in (0, h) and continuous on [0, h], it follows from the Mean Value Theorem that

Thus |θh| < δ and so 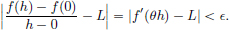
So for all h ∈ (0, δ), 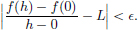
Applying the Mean Value Theorem on [−h, 0], where 0 < h < δ, we also get

for all h ∈ (−δ, 0). Consequently, for all h satisfying 0 < |h| < δ, we have
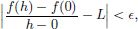
that is, f is differentiable at 0, and 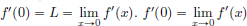
shows that f′ is continuous at 0. It was given that f′ is also continuous on R∗. So f is continuously differentiable on R.
(2)Applying the result from part (1) above, to the function f(n−1) : R → R, we obtain that f(n−1) is continuously differentiable on R, that is, f is n times continuously differentiable on R.
(3)We’ll show that for x > 0,  where pk is a polynomial.
where pk is a polynomial.
This holds for k = 1: f(x) = e−1/x for x > 0, and so 
If the claim holds for some k, then

where  is a polynomial.
is a polynomial.
Now e1/x e−1/x = 1, and since we have  it follows that
it follows that 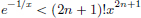 for x > 0. So 0 < x−2n e−1/x < (2n + 1)!x for x > 0. Thus
for x > 0. So 0 < x−2n e−1/x < (2n + 1)!x for x > 0. Thus 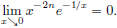 Consequently
Consequently

By the previous part, it follows that f ∈ C∞(R).
Solution to Exercise 6.2, page 232
The equation  says that u is constant along the lines parallel to the x-axis. So for each fixed y, there is a number Cy such that u(x, y) = Cy for all x ∈ R. But u ∈ D(R2) must have compact support, and so it is zero outside a ball B(0, R) with a large enough radius R. So Cy is forced to be 0 for all y! Hence u ≡ 0 is the only solution.
says that u is constant along the lines parallel to the x-axis. So for each fixed y, there is a number Cy such that u(x, y) = Cy for all x ∈ R. But u ∈ D(R2) must have compact support, and so it is zero outside a ball B(0, R) with a large enough radius R. So Cy is forced to be 0 for all y! Hence u ≡ 0 is the only solution.
Solution to Exercise 6.3, page 232
It is clear that if Φ ∈ D(R), then Φ′ ∈ D(R). Moreover,

So we have 
Now suppose that φ ∈ D(R) is such that 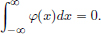
Define Φ by 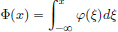 for x ∈ R. Then Φ′ = φ, and so Φ ∈ C∞.
for x ∈ R. Then Φ′ = φ, and so Φ ∈ C∞.
If a > 0 is such that φ is zero outside [−a, a], then we have for x < −a that

On the other hand, for 
So φ also vanishes outside [−a, a], and hence Φ ∈ D(R).
Finally, let φ ∈ Y, and suppose that Φ1, Φ2 ∈ D(R) are such that  Then (Φ1 − Φ2)′ = 0, and so Φ1 − Φ2 = C, where C is a constant. But as Φ1, Φ2 both have compact supports, it follows that C must be zero. Hence Φ1 = Φ2.
Then (Φ1 − Φ2)′ = 0, and so Φ1 − Φ2 = C, where C is a constant. But as Φ1, Φ2 both have compact supports, it follows that C must be zero. Hence Φ1 = Φ2.
Solution to Exercise 6.4, page 233
From the solution to Exercise 6.3, page 232, we know that the Φns are given by

As  there is some a > 0 such that all the φn vanish olutside [−a, a].
there is some a > 0 such that all the φn vanish olutside [−a, a].
Then it follows that each Φn also vanishes outside [−a, a]. Also,

Hence it follows that (Φn)n∈N converges uniformly to 0 as n → ∞. Since  it follows that
it follows that  for k
for k  1. Thus for each k
1. Thus for each k  1, we have that
1, we have that  converges uniformly to 0 (thanks to the fact that
converges uniformly to 0 (thanks to the fact that  This completes the proof that
This completes the proof that 
Solution to Exercise 6.5, page 236
Suppose that such a function δ exists. Let 
For n ∈ N, and let φn : R → R be defined by φn(x) := φ(nx), x ∈ R.
Then φn is smooth, takes values in [0, 1], and vanishes outside [−1/n, 1/n]. So we have
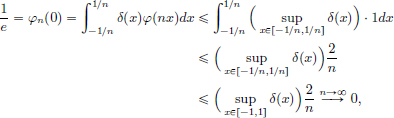
a contradiction.
Solution to Exercise 6.6, page 237
(1)For all φ ∈ D(R), there exists an N ∈ N such that φ = 0 on R\[−n, n].
So the sum in the definition of 〈T, φ〉 is finite: 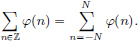
Hence 〈T, φ〉 is well defined for each φ ∈ D(R). The linearity is obvious.
Now suppose that  Then there exists an K ∈ N such that each φn, vanishes outside [−K, K]. Also, for all |k|
Then there exists an K ∈ N such that each φn, vanishes outside [−K, K]. Also, for all |k|  K,
K, 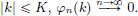
Thus  and so T ∈ D′(R).
and so T ∈ D′(R).
(2)Take any φ ∈ D(R) that is positive in (0, 1q and zero outside [0, 1].
(From Example 6.1, page 230, there is a ψ ∈ D(R) that is positive on (−1, 1) and zero outside [−1, 1]. By shifting and scaling, we see that the function φ defined by φ(x) := ψ(2x − 1), x ∈ R, is one such function.)
Now define φn ∈ D(R), n ∈ N, by 
We have for k ∈ N that 
Thus for all 
Hence for all k  0, we have
0, we have 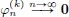 uniformly. However, we have
uniformly. However, we have

(3)There is no contradiction to our conclusion from (1) that T is a distribution, since we observe that there is no compact set K ⊂ R such that for all n ∈ N, φn is zero outside K: Indeed, 
Solution to Exercise 6.7, page 241
The function  is continuously differentiable on R\{0}, and has a jump f(0+) − f(0−) = 1 at 0. For x < 0, H(x) = 0 and so (H(x) cos x)′ = 0.
is continuously differentiable on R\{0}, and has a jump f(0+) − f(0−) = 1 at 0. For x < 0, H(x) = 0 and so (H(x) cos x)′ = 0.
For x > 0, H(x) = 1, and so (H(x) cos x)′ = (cos x)′ = − sin x.
Moreover, 
Consequently, 
The function  is continuously differentiable on R\{0}, and has a jump g(0+) − g(0−) = 0 at 0. For x < 0, H(x) = 0 and so (H(x) sin x)′ = 0.
is continuously differentiable on R\{0}, and has a jump g(0+) − g(0−) = 0 at 0. For x < 0, H(x) = 0 and so (H(x) sin x)′ = 0.
For x > 0, H(x) = 1, and so (H(x) sin x)′ = (sin x)′ = cos x.
Moreover, 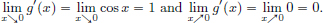
Consequently, 
Solution to Exercise 6.8, page 241
The function  is continuously differentiable on R\{0}, and has a jump f(0+) − f(0−) = 0 at 0. Moreover, for x > 0, |x|/2 = x/2, and so we have (|x|/2)′ = (x/2)′ = 1/2 for x > 0. On the other hand, for x < 0, |x|/2 = −x/2, and so we obtain (|x|/2)′ = (−x/2)′ = −1/2 for x < 0.
is continuously differentiable on R\{0}, and has a jump f(0+) − f(0−) = 0 at 0. Moreover, for x > 0, |x|/2 = x/2, and so we have (|x|/2)′ = (x/2)′ = 1/2 for x > 0. On the other hand, for x < 0, |x|/2 = −x/2, and so we obtain (|x|/2)′ = (−x/2)′ = −1/2 for x < 0.
Also, 
Hence 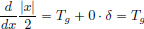 where
where 
Again, g is continuously differentiable on R\{0}.
g has a jump of g(0+) − g(0−) =  − (−
− (−  ) = 1 at 0.
) = 1 at 0.
Also g is constant for x > 0 (respectively for x < 0), and so g′(x) = 0 for x > 0 (respectively for x < 0).
Also, 
Hence 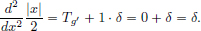
Solution to Exercise 6.9, page 241
(1)Let us first consider the case when ℓ ≡ 0.
Then V = ker ℓ ⊂ ker L implies that ker L = V too, and so L = 0 as well.
Thus we may simply take c = 0, and then clearly L = 0 = 0ℓ is valid.
Now let us suppose that ℓ ≠ 0.
Then there is a vector v0 ∈ V such that ℓ(v0) ≠ 0.
This vector v0 must be nonzero, for otherwise ℓ(v0) = 0.
(To show the desired decomposition of an arbitrary vector as v = cvv0 + w,
with w ∈ ker ℓ, we need to find the appropriate scalar cv, because then we can set w := v − cvv0. To find what cv might work, we apply ℓ on both sides to obtain ℓ(v) = cvℓ(v0) + ℓ(w) = cvℓ(v0) + 0 = cvℓ(v0).
So it seems that  should do the trick!)
should do the trick!)
Given v ∈ V, we now proceed to show that 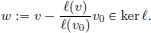
We have  and so w ∈ ker ℓ.
and so w ∈ ker ℓ.
As w ∈ ker ℓ ⊂ ker L, we have L(w) = 0, and

Hence with  we have L = cℓ.
we have L = cℓ.
(2)For φ ∈ D(R), 0 = 〈0, φ〉 = 〈T′, φ〉 = −〈T, φ〉. So {φ′ : φ ∈ D(R)} ⊂ ker T.
Let 1 denote the constant function R ∋ x  1. By Exercise 6.3, page 232
1. By Exercise 6.3, page 232

Finally, by part (1), applied to the vector space V = D(R), with L := T and ℓ := T1, we get the existence of a c ∈ C so that T = cT1 = Tc.
(Here Tc denotes the regular distribution corresponding to the constant function taking value c everywhere on R.)
Solution to Exercise 6.10, page 242
Fix any φ0 ∈ D(R)\{0} which is nonnegative everywhere. For ψ ∈ D(R), set

As ψ and φ0 belong to D(R), so does φ. Moreover,

Thus 
By Exercise 6.3, page 232, there is a unique Φ ∈ D(R) such that Φ′ = φ.
We define S : D(R) → C by 〈S, ψ〉 = −〈T, Φ〉. Let us check that S is linear.
Let ψ1, ψ2 ∈ D(R), and let Φ1, Φ2 ∈ D(R) be such that

Then 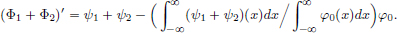
So 
Similarly, 〈S, αψ〉 = α〈S, ψ〉 for all ψ ∈ D(R) and all α ∈ C.
Now we check the continuity of S. Let (ψn)n∈N be a sequence in D(R) such that  . Then there exists an a > 0 such that all the ψn vanish outside [−a, a], and (ψn)n∈N converges uniformly to 0 as n → ∞, giving
. Then there exists an a > 0 such that all the ψn vanish outside [−a, a], and (ψn)n∈N converges uniformly to 0 as n → ∞, giving

Now set 
Then there exists a b > 0 such that each φn vanishes outside [−b, b].
Also, for k  0,
0, 
So for each k  0,
0,  converges uniformly to 0. Thus
converges uniformly to 0. Thus 
Let Φn be the unique element in D(R) such that 
From Exercise 6.4, page 233, we can conclude that 
Consequently, 〈S, ψn〉 = −〈T, Φn〉 → 0 as n → ∞. Hence S ∈ D′(R).
Finally, we’ll show that S′ = T.
If Φ ∈ D(R), then 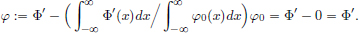
Thus 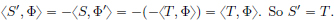
Solution to Exercise 6.11, page 242
Let φ ∈ D(R) be such that φ(0) ≠ 0. (For example we can simply take the test function from Example 6.1, page 230.) Then xn φ ∈ D(R) too, and we have

So δ(n) ≠ 0.
Solution to Exercise 6.12, page 242
It is enough to show the linear independence of δ, δ′, · · ·, δ(n) for each n. Suppose that there are scalars c0, c1, · · ·, cn such that  Let φ ∈ D(R), and for λ > 0, set φλ(x) := φ(λx), for all x ∈ R. Then
Let φ ∈ D(R), and for λ > 0, set φλ(x) := φ(λx), for all x ∈ R. Then

The polynomial  is zero on {λ : λ > 0}, and hence must be identically zero. So c0φ(0) = · · · = cn φ(n)(0) = 0. As the choice of φ was arbitrary, we have that for all test functions φ ∈ D(R),
is zero on {λ : λ > 0}, and hence must be identically zero. So c0φ(0) = · · · = cn φ(n)(0) = 0. As the choice of φ was arbitrary, we have that for all test functions φ ∈ D(R),

But if we look at the φ from Example 6.1, page 230, then φ(0) ≠ 0, and also xnφ, n ∈ N, belongs to D(R), which moreover satisfies

So using φ, xφ, · · ·, xnφ as the test functions in (∗), we obtain c0 = · · · = cn = 0.
Solution to Exercise 6.13, page 242
For any φ ∈ D(Rd), we have

So 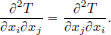
Solution to Exercise 6.14, page 242
 and so it defines a regular distribution on R2.
and so it defines a regular distribution on R2.
For φ ∈ D(R2), with a > 0 such that φ ≡ 0 on R2\(−a, a)2, we have

Thus 
Solution to Exercise 6.15, page 242
If u : R2 → R is a radial function, say u(x) = f(r), where r = ||x||2, then

Thus  Since for all R > 0 we have
Since for all R > 0 we have

we conclude that 
For φ ∈ D(R2) which vanishes outside the ball B(0, R), we have

(log r)(Δφ) is integrable, as logr is locally integrable, and Δφ = 0 outside a ball.

Using Green’s formula in the annulus Ω := {x ∈ R2 :  < ||x||2 < R} (with the boundary ∂Ω being the union of the two circles S(
< ||x||2 < R} (with the boundary ∂Ω being the union of the two circles S( ) = {x : ||x||2 =
) = {x : ||x||2 =  } and S(R) = {x : ||x||2 = R}), for the functions u = log r and v = φ, we obtain
} and S(R) = {x : ||x||2 = R}), for the functions u = log r and v = φ, we obtain

We’ll show below that the first integral on the right-hand side is O( ), and thus it tends to 0 as
), and thus it tends to 0 as  → 0.
→ 0.
As  and ||n(x)||2 = 1, the Cauchy-Schwarz Inequality gives
and ||n(x)||2 = 1, the Cauchy-Schwarz Inequality gives

where  Finally,
Finally, 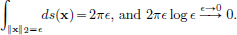
Next we will look at the second integral 
First, 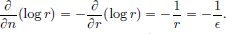 Moreover,
Moreover,

Given η > 0,
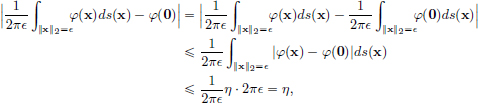
where first  0 > 0 is chosen small enough so that |φ(x) − φ(0)|
0 > 0 is chosen small enough so that |φ(x) − φ(0)|  η if ||x||2
η if ||x||2 
 0, and
0, and  satisfies 0 <
satisfies 0 < 

 0.
0.
Thus 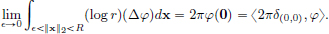
So  Hence
Hence 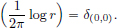
Solution to Exercise 6.16, page 248
u is continuous on R, and continuously differentiable on R\{0}.
For x < 0, we have u′(x) = 0. For x > 0, u′(x) = 1.
Also, 
Thus by the Jump Rule,  in the sense of distributions.
in the sense of distributions.
So u is a weak solution of u′ = H.
Solution to Exercise 6.17, page 251
We view H(x) cosx as the product of the C∞ function cos with the regular distribution H. Using the Product Rule, we have

Similarly,

Solution to Exercise 6.18, page 251
(1)We have
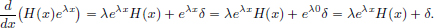
Hence 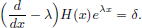
(2)When 
If the claim is true for some n ∈ N, then

So the claim follows for all n ∈ N by induction.
(3)We have


Consequently, 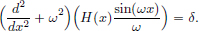
Solution to Exercise 6.19, page 252
We have for all φ ∈ D(R) that

So αδ′ = α(0)δ′ − α′(0)δ. In particular, xδ′ = 0δ′ − 1δ = −δ.
Solution to Exercise 6.20, page 252
For all φ ∈ D(R), we have that

So 
Solution to Exercise 6.21, page 252
With u := e−3yxH(y), we have

For all φ ∈ D(R2), we have
So  Hence
Hence 
Moreover, u(0, y) = e−0 H(y) = 1 · H(y) = H(y).
Solution to Exercise 6.22, page 252
First we note that for all φ ∈ D(R), we have

where 1 is the constant function R ∋ x  1.
1.
Suppose on contrary, it is possible to define an associative and commutative product such that for α ∈ C∞(R) and T ∈ D′(R), it agrees with Definition 6.6, page 249. Then

whereas

and so  violating associativity.
violating associativity.
Solution to Exercise 6.23, page 252
(1)Let  Then we have
Then we have

From Exercise 6.9, page 241, there exists a c ∈ C such that e−λxT = c, that is, T = ceλx.
(2)Since f ∈ C∞, there exists an F ∈ C∞ such that 
(In fact, an explicit expression for one such F (for which F(0) = 0), is given by 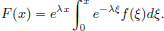 This can be checked by differentiation using the Product Rule and the Fundamental Theorem of Calculus.)
This can be checked by differentiation using the Product Rule and the Fundamental Theorem of Calculus.)
Hence we obtain 
From part (1), T − F = ceλx for some c ∈ C. Hence T = F + ceλx ∈ C∞.
Then 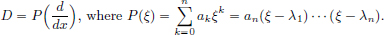
So P(ξ) = (ξ − λ)Q(ξ), where λ = λn, and a suitable polynomial Q.
Correspondingly, with 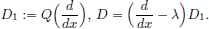
We’ll use induction (on the order n of D) to prove

This is true for n = 1, from part (2) above.
Suppose that the claim is true for all differential operators of order n.
Let D have order n + 1, and write 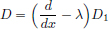 where D1 is order n.
where D1 is order n.
If DT = f ∈ C∞, then  and so D1T = Tg for some g ∈ C∞.
and so D1T = Tg for some g ∈ C∞.
But by the induction hypothesis, it now follows that T = TF, with F ∈ C∞.
(4)If E is also a fundamental solution, then DE = δ.
But also DE∗ = δ, and so D(E − E∗) = 0.
Thus E − E∗ = F, where F is a classical solution of the homogeneous equation DF = 0. So E = E∗ + F.
Conversely, if F is a classical solution of the homogeneous equation DF = 0, then E := E∗ + F is a fundamental solution of D too: indeed, we have that DE = DE∗ + DF = δ + 0 = δ.
So we conclude that: E ∈ D′(R) satisfies DE = δ if and only if

Solution to Exercise 6.24, page 252
If T = cδ, where c ∈ C, then clearly xT = x(cδ) = 0.
Now suppose that T ∈ D′(R) is such that xT = 0.
This means that for all φ ∈ D(R), we have 0 = 〈xT, φ〉 = 〈T, xφ〉.
Hence {xφ : φ ∈ D(R)} ⊂ ker T. We will now identify the set on the left-hand side as ker δ = {ψ ∈ D(R) : ψ(0) = 0}, and then use part (1) of Exercise 6.9, page 241.
First, let us note that if ψ = xφ, where φ ∈ D(R), then ψ ∈ D(R), and moreover, ψ(0) = 0φ(0) = 0. So we have {xφ : φ ∈ D(R)} ⊂ {ψ ∈ D(R) : ψ(0) = 0}.
Next, let us show the reverse inclusion. Let ψ ∈ D(R) be such that ψ(0) = 0.
We have, by the Fundamental Theorem of Calculus:

By differentiating under the integral sign we see that φ ∈ C∞.
If ψ is zero outside [−a, a] for some a > 0, then as 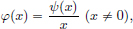
it follows that φ also vanishes outside [−a, a]. Thus φ ∈ D(R).
So we have {ψ ∈ D(R) : ψ(0) = 0} ⊂ {xφ : φ ∈ D(R)} as well.
Thus ker δ = {xφ : φ ∈ D(R)} ⊂ ker T, and by part (1) of Exercise 6.9, page 241 there exists a c ∈ C such that T = cδ.
Solution to Exercise 6.25, page 254
First, we prove by induction that  where pn is a polynomial.
where pn is a polynomial.
This is indeed true for n = 0 and 
If it is true for some n, then

where  is a polynomial.
is a polynomial.
This finishes the proof of our claim.
Now to show e−x2 ∈ S(R), it is enough to show that 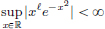 for all nonnegative integers ℓ. For ℓ = 0, this is clear since |e−x2|
for all nonnegative integers ℓ. For ℓ = 0, this is clear since |e−x2|  1 for all x ∈ R.
1 for all x ∈ R.
We have  and so for
and so for 
Since  is a continuous function, there is an M > 0 such that
is a continuous function, there is an M > 0 such that 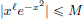
for x ∈ [−1, 1]. Consequently, 
Solution to Exercise 6.26, page 254
Since 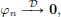 we know that there exists an a > 0 such that all the φn vanish outside [−a, a], and moreover, φn and all its derivatives converge uniformly to 0 on [−a, a]. So for any nonnegative integers m, k, we have that
we know that there exists an a > 0 such that all the φn vanish outside [−a, a], and moreover, φn and all its derivatives converge uniformly to 0 on [−a, a]. So for any nonnegative integers m, k, we have that

So 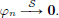
Solution to Exercise 6.27, page 255
We have for φ ∈ S(R) that

From here it follows that if (φn)n∈N is a sequence in S(R) such that  as n → ∞, then 〈Tf, φn〉 → 0. Thus Tf ∈ S′(R).
as n → ∞, then 〈Tf, φn〉 → 0. Thus Tf ∈ S′(R).
Solution to Exercise 6.28, page 256
For φ ∈ S(R), we have that

Note that in the last step, we have used the fact that the Fourier transform of an L′(R) function is bounded on R, and hence it defines a tempered distribution.
1 See for example [Sasane (2015), §2.4].
2 See for example [Sasane (2015), Chapter 6].
3 The symbol ¬ stands for “negation”. It is read as: “It is not the case that · · ·”.
4 See for example [Sasane (2015), page 311].
5  uj = 0, unless i = i, in which case
uj = 0, unless i = i, in which case  ui = 1. Here ·
ui = 1. Here · denotes transpose.
denotes transpose.
6 By the Axiom of Choice!