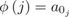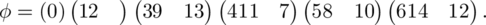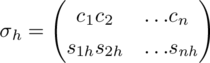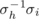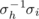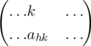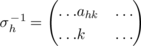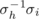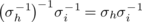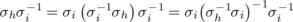Latin squares with particular properties
In Section 2.1, we discussed quasigroups of some special types and their associated latin squares. Also, in Section 2.6, we introduced complete latin squares. Here, we discuss latin squares with various other special properties most of which had not been thought of when [DK1] was published.
9.1 Bachelor squares
The name bachelor square for a latin square which has no orthogonal mate was introduced by Van Rees(1990) who drew attention to Mann’s theorem of 1944 on this subject (which applies to squares of orders 4m + 1 and 4m + 2 [see Theorem 5.1.6]) and who proved for the case of latin squares of order 4m + 3 that (i) such a square can be in a set of at most 2m + 2 MOLS if it contains a latin subsquare of order 2m + 1; and (ii) that there exist latin squares of such orders which cannot be in a set of three MOLS. Statement (i) had earlier been proved by Drake(1977). See Theorem 5.2 of Chapter 2 in [DK2].
Clearly, a latin square which has no transversals is a bachelor square so, in particular, cyclic squares of even order and latin squares of q-step type are bachelor squares. (See Section 4.5.)
It follows as a corollary to Mann’s theorem that if a latin square L is of order 4m + 2 and contains a latin subsquare of order 2m + 1 or if it is of order 4m + 1 and contains a latin subsquare of order 2m then L is a bachelor square. However, this leaves completely open the question for which orders n ≡ 3 mod 4 (other than 3 itself) bachelor squares exist.
The general question “For which orders do bachelor squares exist?” was solved almost simultaneously by Wanless and Webb(2006) and by A.B.Evans(2006) using a similar method: namely, to modify a certain latin square by exchanging the elements in particular cells. However, the proof given by the first two authors has the virtue of elegance and of being applicable to latin squares of all orders, not just those of form 4m + 3. These authors showed that, for every order n > 3, there exists a latin square which contains a cell that is not included in any transversal. We gave their proof in Section 3.5. Since a latin square which has an orthogonal mate has a decomposition into disjoint transversals of which precisely one must pass through every cell, it follows at once that bachelor squares exist of every order except three.
9.2 Homogeneous latin squares
For example, a cyclic latin square of order 4 is 1-homogeneous whereas a latin square of order 4 based on Klein’s Viergruppe Z 2 × Z 2 is 3-homogeneous.
A latin square which is 0-homogeneous has also been called an N 2-square. (In this notation, a latin square which has no latin subsquares of any size is an N ∞-square. We discuss these in Section 9.4.) By combining the results obtained in a series of papers, it was proved in the late 1970s that N 2-squares exist for all orders n except n = 2 and 4. Details of the proof are given on pages 113-116 of [DK2].
To return to h-homogeneous latin squares, it is easy to see that 1-homogeneous latin squares exist only of even orders and that (n − 2)-homogeneous latin squares of order n do not exist since any such square must in fact be (n − 1)-homogeneous. Also, (n − 1)-homogeneous latin squares exist if and only if n is a power of 2. See Heinrich and Wallis(1981). It was shown in Hobbs, Kotzig and Zacs(1982) that (n − 3)-homogeneous latin squares exist if and only if n ∈ {3, 4, 6, 8, 12, 16}. Killgrove(2001) called a 1-homogeneous latin square two-tiled and he proved:
In two unpublished papers by D’Angelo and Turgeon and by Abrham and Kotzig, these authors obtained some further results; in particular, the latter authors show that 4-homogeneous latin squares do not exist if n < 8 but that they do exist of all orders n = 8k. (This leaves open the question whether and/or for which other orders such squares exist.) The former authors mention and/or prove several results: (i) There are 2-homogeneous latin squares of all orders divisible by 4 except 4 itself; (ii) If n = 4k and k ≥ 1, there is an (n − k)- or (n − k + 1)-homogeneous latin square of order n according as k is odd or even; (iii) If A is an h-homogeneous latin square of order m and B is a k-homogeneous latin square of order n, then A × B is an (hk + h + k)-homogeneous latin square of order mn (where A × B denotes the direct product of the quasigroups whose Cayley tables are defined by A and B); (iv) The Cayley table of a group G is an h-homogeneous latin square, where h is the number of elements of order 2 in G (cf. Killgrove’s lemma above). From (iv) it follows that, for each positive integer h ≥ 2, there is an h-homogeneous or (h + 1)-homogeneous latin square of order 2h according as h is odd or even. This last result makes use of the dihedral groups and had already been proved earlier in Heinrich and Wallis(1981) and in Hobbs, Kotzig and Zaks(1982).
So far as the present author is aware, the complete spectrum of integers h for which h-homogeneous latin squares exist is still an open question. But Hobbs and Kotzig(1983) contains a summary of results which were known at the time that paper was written regarding squares of orders up to 26. Another interesting question is: For which integers h do orthogonal h-homogeneous latin squares exist or, alternatively, can it be proved that they do not exist for some values of h? This question is partly answered by remark (iv) above. We notice, for example, that the three mutually orthogonal latin squares which are based on Klein’s Viergruppe are all 3-homogeneous.
9.3 Diagonally cyclic latin squares and Parker squares
A latin square of order n is said to be diagonally cyclic (or sometimes, and more accurately, left diagonally cyclic) if each of its left-to-right broken diagonals contains each of its n symbols and each is a cyclic permutation of the main left-to-right diagonal. If the same statement is true for the right-to-left diagonals also, the square is called totally diagonal or to be a Knut Vik design, see page 219. Two examples of the latter type of square are given in Figure 6.3.1.
The term “diagonally cyclic” is due to Franklin(1984a,b) who was probably the first to discuss construction of such squares explicitly. He also used what he called “bordered cyclic latin squares” (obtained by a prolongation of a diagonally cyclic latin square) to construct orthogonal latin squares and, in particular, pairs of MOLS of order 10. However, Franklin was certainly not the first to conceive and make use of the latter idea.
In the papers already referred to, Franklin frequently abbreviated “diagonally cyclic” to “cyclic”. However, not all left diagonally cyclic latin squares are cyclic in the sense used elsewhere in this book: that is, isotopic to a multiplication group of the cyclic group of the same order. A smallest counter-example, kindly supplied by Ian Wanless, is given in Figure 9.3.1. Wanless remarks that this is the multiplication table of a Steiner quasigroup of order 7 and that it cannot be isotopic to (Z 7, +) because it has too many subsquares, also that it is smallest because (see Theorem 9.3.1) all orthomorphisms of (Z n , +) for n ≤ 5 are linear 1 and so define cyclic groups.

Fig. 9.3.1
A left diagonally cyclic latin square A = ‖aij ‖ is completely determined by its first row (or column) and by the order of the symbols in the main left-to-right diagonal. To see this, suppose that the latter order is ao , a 1, …, an −1. We regard the square as a collection of ordered triples, say (i, j, aij ), as we did on page 14. Then, if (i, j, ak ) is a triple, so is (i + 1, j + 1, ak +1) where arithmetic is modulo n.
In Bedford(1995), that author showed that:
Later, Bedford [see Bedford(1998b)] used the fact that a diagonally cyclic latin square A can be constructed by putting aij = φ(j − i) + i to obtain his example of a non-cyclic latin square of order 15 with property P as defined in Section 9.4. The orthomorphism of (Z 15, +) which he used was
Since each broken diagonal of a left diagonally cyclic latin square of order n is a transversal, such a square can be n times prolonged and this fact has been exploited by very many authors including Parker(1959b) who used it (though not explicitly as he described his construction in the language of orthogonal arrays) to disprove Euler’s conjecture by constructing for the first time a pair of MOLS of order 10 and, more generally, a pair of MOLS of order (3q − 2)/2, where q is any prime power congruent to 3 modulo 4. Yamamoto(1961) and, later, Hedayat and Seiden(1971,1974) under the title of sum composition used the idea of multiple prolongation 2 to construct t MOLS of order n + m from t +1 MOLS of order n and t MOLS of order m (n > 2m). The required procedure is described in detail on pages 436-442 of [DK1]. The method has been generalized and also re-presented in a more easily understood form by Guérin(1966b) and this author has christened it “Yamamoto’s method”. For some related constructions and for a proof that, as t → ∞, the number of non-equivalent pairs of MOLS of order t also tends to infinity, the reader is referred to chapter 6 of Guérin(1966b) and also to Barra and Guérin(1963a,b) and Guérin(1963a,b,1964,1966a).
In Wanless(2004b), that author has made the following definition: We adjoin b infinity symbols to the cyclic group Z
m
to obtain the set Z
m
,b
= Z
m
⋃ {∞1, ∞2, … ∞
b
} and we define z
+ for z ∈ Z
m
,b
by z
+ = z + 1 mod m if z ∈ Z
m
and z
+ = z otherwise. Then a bordered diagonally cyclic latin square (henceforward to be called a Parker square, see below) with rows, columns and symbols indexed by Z
m
,b
is one for which the presence of any triple (i, j, aij
) implies that the triple (i
+, j
+,
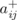 ) also occurs in the square. We say that this Parker square is of Bb
-type if it is based on Z
m
,b
in the above way for m ≥ 1 or if its symbols can be mapped bijectively to Z
m
,b
in such a way that the resulting square has the above properties.
) also occurs in the square. We say that this Parker square is of Bb
-type if it is based on Z
m
,b
in the above way for m ≥ 1 or if its symbols can be mapped bijectively to Z
m
,b
in such a way that the resulting square has the above properties.
It was because of the important role which squares of Bb -type played in the disproof of Euler’s conjecture that Wanless christened them Parker squares. In fact, the pair of MOLS of order 10 obtained by Parker and illustrated in Figure 9.3.2 is of B 3-type. Here, the integers 7, 8, 9 play the roles of ∞1, ∞2, ∞3. This pair of squares could have been constructed directly by sum composition from a triple of MOLS of order 7 of which the first has constant left-to-right diagonals and the remaining two are diagonally cyclic (shown in Figure 9.3.3) and a pair of MOLS of order 3. 3
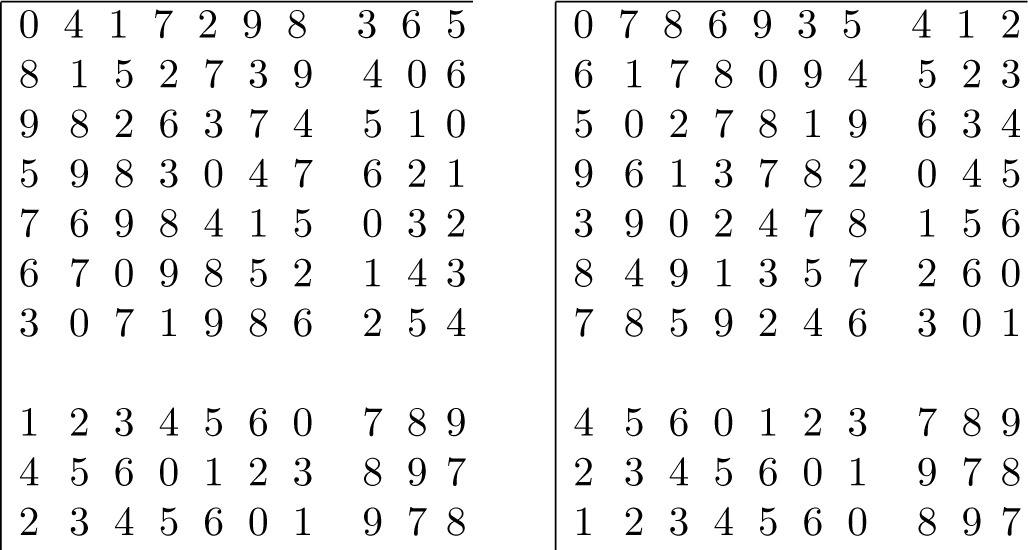
Fig. 9.3.2

Fig. 9.3.3
In his paper of 2004, Wanless has extended Theorem 9.3.1 to provide necessary and sufficient conditions for a Parker square of any given Bi -type to exist by introducing the idea of a partial orthomorphism of (Zm , +). (In the case of a B 1-type Parker square, this is the same as a near orthomorphism. See Section 7.6.)
In the same paper, he has given an example of a B 1-type square and a B 2-type square which are quasigroup isomorphic: that is, there exists an isotopism which transforms one square to the other and which re-labels the rows, columns and symbols in the same way. Thus, Parker squares of different types may lie in the same isomorphism class and, a fortiori, in the same isotopism or main class of latin squares. Also, the B 2-type Parker square given by Wanless illustrates the fact that not all Parker squares can be contracted to diagonally cyclic latin squares.
We note that the diagonally cyclic latin squares in Figure 9.3.3 are orthogonal. A number of authors (including Franklin) have discussed the conditions for a diagonally cyclic latin square to have one or more orthogonal mates which are also diagonally cyclic. Since each such square is orthogonal to the latin square with the property that all the cells of each broken left-to-right diagonal contain the same fixed element, the maximum number of left diagonally cyclic squares of order n which are mutually orthogonal cannot exceed n − 2 by Theorem 5.1.2. Wanless(2004b) has shown more generally that, given arbitrary integers n and b, there cannot be more than n − 1 if b = 1 or min[N(b), (n − b/b] if b > 1 mutually orthogonal Bb -type latin squares of order n. He has further shown that both these bounds can be attained.
The Wanless paper of 2004 contains many further results concerning Parker squares and also it lists a surprisingly large number of papers whose authors had made use of such squares for their constructions up to the time when that paper was published. For example, Owens and Preece(1996) constructed their non-cyclic latin squares of prime order p ≥ 11 with property P (see Section 9.4) by modifying a Parker square of B 1-type. In particular, Wanless himself, in collaboration with Bryant and Maenhaut [see Bryant, Maenhaut and Wanless(2006)] has used such squares to construct infinite families of atomic latin squares (again see Section 9.4 for the definition) which are of B 1-type.
A number of the papers cited by Wanless had also been mentioned earlier in Bedford(1993) and in the latter paper the close connection between left diagonally cyclic latin squares and neofields had been shown: namely, the addition table for a cyclic neofield of even order can always be obtained by the prolongation of an appropriate left diagonally cyclic latin square taking its main diagonal as the transversal.
Parker squares continue to be valuable as a means of obtaining new results.
Finally, let us mention a paper [Cavenagh and Wanless(2010)] in which the authors show that the number of transversals in Cayley tables of cyclic groups of odd order increases exponentially with the order and they remark that, by virtue of Theorem 9.3.1, the number of diagonally cyclic latin squares likewise increases exponentially with the order of the square.
9.4 Non-cyclic latin squares with cyclic properties
One of the rare occasions when the authors of the first edition of the present book were in serious disagreement was when the question arose in the late 1980s (in connection with their research) as to whether a given latin square of prime order p with the property that each of its rows was a cyclic permutation of the first row would necessarily be isotopic to the cyclic group of order p. Dénes was strongly of the opinion that it would while Keedwell was equally strongly of the opinion that it would not. The issue was resolved when the two authors constructed counter-examples in Dénes and Keedwell(1988) for latin squares not only of prime orders but for all orders n ≥ 7. Shortly afterwards, a simpler construction of counter-examples was given in Keedwell(1991).
Next, in the development of the idea of constructing non-cyclic latin squares with cyclic properties, Owens and Preece(1996) constructed, for all prime orders p ≥ 11, a latin square with the stronger property P that the permutation from row i to row j is cyclic for all i and j, j ≠ i. The earlier construction only gave a square which had property P for the permutation from row 0 to row j, 1 ≤ j ≤ n − 1 (in the case of a latin square of order n). Let us remark here that every cyclic latin square of prime order has property P and also has the similar property for columns. On the other hand, no latin square of composite order based on a group has property P. (See below.) Despite this, Bedford(1998b), in an unpublished paper (see Section 9.3), gave an example of a latin square of order 15 which has property P.
The next step came when Wanless(1999) observed that every latin square L of order n defines a 1-factorization of the complete bipartite graph Kn ,n (and in several ways, see Section 8.3). He also observed that a latin square L having property P would not contain any proper latin subsquare M because, if rows i and j of L both contained rows of such a subsquare M, then the permutation from row i to row j of L would include one or more sub-cycles involving only the elements of M. That is, any latin square with property P is an N ∞-square and conversely.
Let L be as above and let one partite set {c 1, c 2, …, cn } of vertices of Kn ,n denote the columns of L and let the second partite set {s 1, s 2, …, sn } denote the symbols. Then each row of L defines a 1-factor as follows: if the symbol sk occurs in column cj of row rh , join cj to sk . Since no two entries in rh are the same, these edges form a 1-factor which corresponds to the permutation
defining row rh
as a permutation from natural order. Also, the 1-factors associated with different rows are disjoint since each column contains each symbol only once. The permutation which maps row rh
to row ri
is then
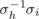 . Each of σh
, σi
defines a 1-factor of Kn
,n
and
. Each of σh
, σi
defines a 1-factor of Kn
,n
and
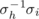 defines a means of traversing the edges of the graph: slh
→ cl
→ sli
→ etc. If property P holds, then
defines a means of traversing the edges of the graph: slh
→ cl
→ sli
→ etc. If property P holds, then
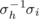 is a full length cycle and all edges of the graph are traversed by the union of the 1-factors corresponding to σh
, σi
. This led Wanless to say that a latin square (or rectangle) with property P is pan-Hamiltonian because of the connection with Hamiltonian decompositions of the complete bipartite graph just described.
is a full length cycle and all edges of the graph are traversed by the union of the 1-factors corresponding to σh
, σi
. This led Wanless to say that a latin square (or rectangle) with property P is pan-Hamiltonian because of the connection with Hamiltonian decompositions of the complete bipartite graph just described.
For example, in Figure 9.4.1 the 1-factors which define the first three rows of L 4 are F 1, F 2, F 3. The unions F 1 ⋃ F 2 and F 1 ⋃ F 3 form Hamiltonian circuits in Kn ,n while F 2 ⋃ F 3 does not. As illustration, the union F 1 ⋃ F 3 gives s 3 → c 1 → s 1 → c 2 → s 4 → c 3 → s 2 → c 4 → s 3. The latin rectangles which are given by the first two rows or the first and third rows are pan-Hamiltonian and so contain no sub-rectangles.
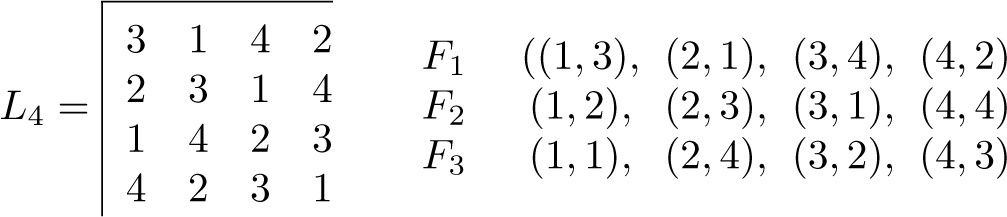
Fig. 9.4.1
Later, Wanless refined the name to row-panHamiltonian since the roles of rows, columns and symbols can be permuted to give parastrophes of L which may be column-panHamiltonian or symbol-panHamiltonian.
In his paper of 1999, Wanless also proved the following three lemmas:
This lemma and with the same proof had earlier been given as a closing remark in the paper of Owens and Preece(1996).
Wanless called a latin square atomic if all six of its parastrophes are pan-Hamiltonian. A latin square is atomic if and only if none of its parastrophes has a proper latin sub-rectangle.
To test whether a given latin square L is atomic, it suffices to check that L, its transpose L (1 2) and the transpose of its row inverse L (2 3)(1 2) = L (1 2 3) are atomic. This follows from the first statement in the proof of Lemma C.
By Theorem 4.2.2, if a latin square L is the Cayley table of a group or of a loop with the inverse property, then all five of its parastrophes are isotopic to it. It follows from Lemma B above that in that case, if L is pan-Hamiltonian then it is in fact atomic. In the Cayley table of a group of order n (which we may assume to be in reduced form), the rows are represented by regular permutations with cycle lengths which divide n and so when and only when 5 n is prime and the group is cyclic, it is pan-Hamiltonian. Thus, the only group-based square which is atomic is that of the cyclic group Cp .
Wanless(1999) used a connection between perfect 1-factorizations of the complete graph Kn +1 and perfect 1-factorizations of Kn ,n which we next describe to obtain two non-isomorphic perfect 1-factorizations of Kp ,p and hence the following result:
“Let p ≥ 11 be a prime. If 2 is a primitive root modulo p, then there exists an atomic square of order p outside the main class of latin squares which contains Cp .”
In a subsequent paper [see Bryant, Maenhaut and Wanless(2006)], these authors used similar ideas to construct five different main classes M !, M 2, M 3, M 4, M 5 of latin squares of prime order which sometimes or always contain atomic latin squares. The squares in M 1 include Cp and so are atomic always. The squares in M 3 include those constructed by Owens and Preece(1996) who showed that they too are atomic. The squares in M 2 include that constructed by Wanless and referred to in the preceding paragraph. These squares are atomic when p is such that it has 2 as primitive root and so also are the squares in M 4 and M 5.
In Maenhaut and Wanless(2004), a complete enumeration of atomic latin squares of order 11 (which is the smallest order for which there are examples distinct from isotopes of Cp ) is given. They belong to seven main classes.
Suppose that the complete graph Kn +1 has a perfect 1-factorization F 1, F 2, …, Fn . We label the vertices of Kn +1 by υ 1, υ 2, …, υn , υ ∞. We denote the 1-factor which contains the edge (υh , υ ∞) by Fh . Let the remaining edges of Fh be …, (υx , υy ), …, etc. Let Kn ,n have partite sets {c 1, c 2, …, cn } and {s 1, s 2, …, sn }. We use Fh to construct a 1-factor F′ h of Kn ,n whose edges are …, (ch , sh ), (cx , sy ), (cy , sx ), …, etc. and thence construct a latin square L whose hth row is given by the involutary permutation σh = (h)(x y)…. If the union of Fh and Fi is a Hamiltonian circuit in Kn +1, then the union of F′ h and F′ i is a Hamiltonian circuit of Kn ,n , since the sequence of vertices → υa → υb → υd → υe →υf →, where (υa , υb ), (υd , υe ), … ∈ Fh and (υb , υd ), (υe , υf ), … ∈ Fi , is replaced by the sequences → ca → sb → cd → se → cf → and → sa → cb → sd → ce → sf → in Kn ,n and the sequence → υh → υ ∞ → υi → by the sequences → ch → sh → and → si → ci →. This construction had earlier been noted and used for various purposes by several authors, in particular see Keedwell(1978), Laufer(1980), Wanless and Ihrig(2005) and page 116 of [DK2]. Note that n + 1 must be even for such a 1-factorization to exist.
As illustration, Figure 9.4.2 gives a perfect 1-factorization of K
6 and the corresponding perfect 1-factorization of K
5,5 and Figure 9.4.3 shows the pan-Hamiltonian latin square L
5 thereby defined. The method of construction shows that this square will always be idempotent and involutary. That is, each row permutation σh
is equal to its own inverse and so L = L
(2 3). By Lemma C, it follows that ν(L) = 2 or 6 for such a square. If rows and symbols are interchanged to obtain the parastroph
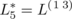 , the latter will be symmetric, idempotent and symbol-panHamiltonian.
, the latter will be symmetric, idempotent and symbol-panHamiltonian.
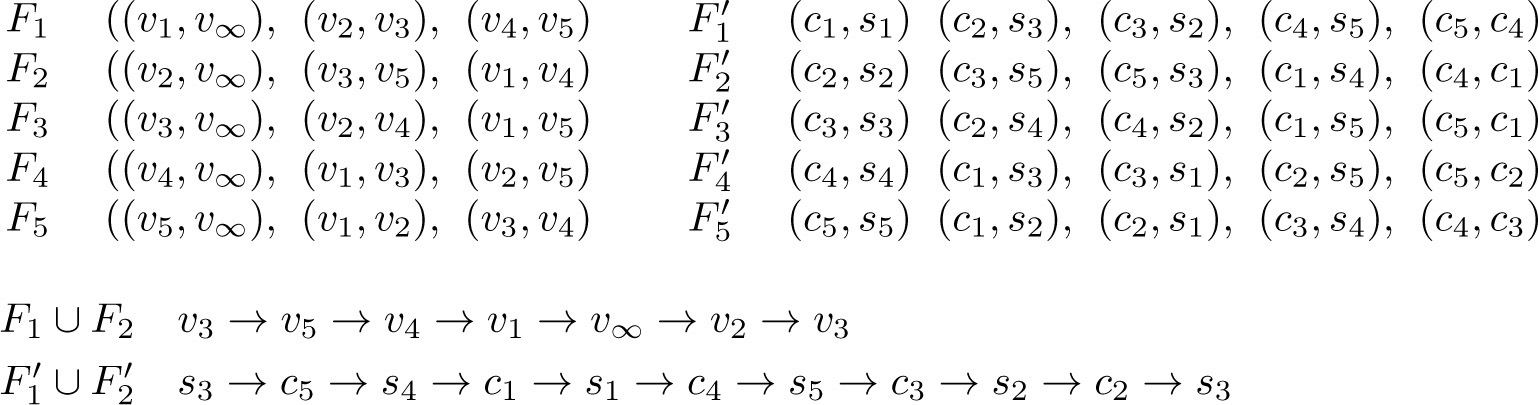
Fig. 9.4.2
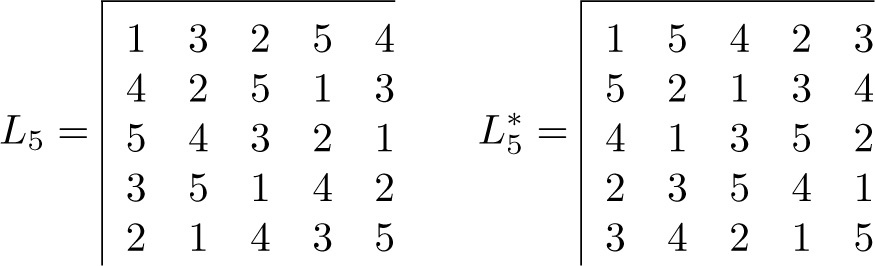
Fig. 9.4.3
Using the above ideas, Wanless(1999) was able to construct an atomic latin square not in the main class which contains Cp for each prime p ≥ 11 for which 2 is a primitive root (as we stated earlier). Wanless also claimed that, by applying his construction procedure to a particular perfect 1-factorization of K 28, he had obtained an atomic latin square of order 27.
In Wanless(2005), the same author used cyclotomic orthomorphisms in finite fields to construct atomic latin squares of other prime power orders but, so far as the present author is aware, no atomic latin square of composite but non-prime-power order has yet been found.
We end this section with a brief discussion of N ∞-squares. Such squares need not be atomic. Andersen and E.Mendelsohn(1982) showed that N ∞-squares exist of all orders n ≠ 2 a 3 b . We outlined their proof in Chapter 4, Section 2 of [DK2]. A further construction of N ∞-squares was devised by Elliott and Gibbons(1992) who obtained subsquare-free latin squares of orders 16 and 18. Later, Maenhaut, Wanless and Webb(2007) showed that if n is odd and divisible by 3, then an N ∞-square of order n exists. (See the bibliography of that paper for some papers on this topic not mentioned here.) Combining this with the earlier paper of Andersen and E.Mendelsohn, we are able to conclude that N ∞-squares exist of all odd orders. However, so far as the present author is aware, the situation regarding even orders is still not completely determined.