Chapter 2. A Crash Course in Python

People are still crazy about Python after twenty-five years, which I find hard to believe.

Michael Palin

All new employees at DataSciencester are required to go through new employee orientation, the most interesting part of which is a crash course in Python.

This is not a comprehensive Python tutorial but instead is intended to highlight the parts of the language that will be most important to us (some of which are often not the focus of Python tutorials). If you have never used Python before, you probably want to supplement this with some sort of beginner tutorial.

The Zen of Python

Python has a somewhat Zen description of its design principles, which you can also find inside the Python interpreter itself by typing “import this.”

One of the most discussed of these is:

There should be one—and preferably only one—obvious way to do it.

Code written in accordance with this “obvious” way (which may not be obvious at all to a newcomer) is often described as “Pythonic.” Although this is not a book about Python, we will occasionally contrast Pythonic and non-Pythonic ways of accomplishing the same things, and we will generally favor Pythonic solutions to our problems.

Several others touch on aesthetics:

Beautiful is better than ugly. Explicit is better than implicit. Simple is better than complex.

and represent ideals that we will strive for in our code.

Getting Python

Note

As instructions about how to install things can change, while printed books cannot, up-to-date instructions on how to install Python can be found in the book’s GitHub repo.

If the ones printed here don’t work for you, check those.

You can download Python from Python.org. But if you don’t already have Python, I recommend instead installing the Anaconda distribution, which already includes most of the libraries that you need to do data science.

When I wrote the first version of Data Science from Scratch, Python 2.7 was still the preferred version of most data scientists. Accordingly, the first edition of the book was based on Python 2.7.

In the last several years, however, pretty much everyone who counts has migrated to Python 3. Recent versions of Python have many features that make it easier to write clean code, and we’ll be taking ample advantage of features that are only available in Python 3.6 or later. This means that you should get Python 3.6 or later. (In addition, many useful libraries are ending support for Python 2.7, which is another reason to switch.)

Virtual Environments

Starting in the next chapter, we’ll be using the matplotlib library to generate plots and charts. This library is not a core part of Python; you have to install it yourself. Every data science project you do will require some combination of external libraries, sometimes with specific versions that differ from the specific versions you used for other projects. If you were to have a single Python installation, these libraries would conflict and cause you all sorts of problems.

The standard solution is to use virtual environments, which are sandboxed Python environments that maintain their own versions of Python libraries (and, depending on how you set up the environment, of Python itself).

I recommended you install the Anaconda Python distribution, so in this section I’m going to explain how Anaconda’s environments work. If you are not using Anaconda, you can either use the built-in venv module or install virtualenv. In which case you should follow their instructions instead.

To create an (Anaconda) virtual environment, you just do the following:

# create a Python 3.6 environment named "dsfs"
conda create -n dsfs python=3.6

Follow the prompts, and you’ll have a virtual environment called “dsfs,” with the instructions:

#
# To activate this environment, use:
# > source activate dsfs
#
# To deactivate an active environment, use:
# > source deactivate
#

As indicated, you then activate the environment using:

source activate dsfs

at which point your command prompt should change to indicate the active environment. On my MacBook the prompt now looks like:

(dsfs) ip-10-0-0-198:~ joelg$

As long as this environment is active, any libraries you install will be installed only in the dsfs environment. Once you finish this book and go on to your own projects, you should create your own environments for them.

Now that you have your environment, it’s worth installing IPython, which is a full-featured Python shell:

python -m pip install ipython
Note

Anaconda comes with its own package manager, conda, but you can also just use the standard Python package manager pip, which is what we’ll be doing.

The rest of this book will assume that you have created and activated such a Python 3.6 virtual environment (although you can call it whatever you want), and later chapters may rely on the libraries that I told you to install in earlier chapters.

As a matter of good discipline, you should always work in a virtual environment, and never using the “base” Python installation.

Whitespace Formatting

Many languages use curly braces to delimit blocks of code. Python uses indentation:

# The pound sign marks the start of a comment. Python itself
# ignores the comments, but they're helpful for anyone reading the code.
for i in [1, 2, 3, 4, 5]:
    print(i)                    # first line in "for i" block
    for j in [1, 2, 3, 4, 5]:
        print(j)                # first line in "for j" block
        print(i + j)            # last line in "for j" block
    print(i)                    # last line in "for i" block
print("done looping")

This makes Python code very readable, but it also means that you have to be very careful with your formatting.

Warning

Programmers will often argue over whether to use tabs or spaces for indentation. For many languages it doesn’t matter that much; however, Python considers tabs and spaces different indentation and will not be able to run your code if you mix the two. When writing Python you should always use spaces, never tabs. (If you write code in an editor you can configure it so that the Tab key just inserts spaces.)

Whitespace is ignored inside parentheses and brackets, which can be helpful for long-winded computations:

long_winded_computation = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 +
                           13 + 14 + 15 + 16 + 17 + 18 + 19 + 20)

and for making code easier to read:

list_of_lists = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

easier_to_read_list_of_lists = [[1, 2, 3],
                                [4, 5, 6],
                                [7, 8, 9]]

You can also use a backslash to indicate that a statement continues onto the next line, although we’ll rarely do this:

two_plus_three = 2 + \
                 3

One consequence of whitespace formatting is that it can be hard to copy and paste code into the Python shell. For example, if you tried to paste the code:

for i in [1, 2, 3, 4, 5]:

    # notice the blank line
    print(i)

into the ordinary Python shell, you would receive the complaint:

IndentationError: expected an indented block

because the interpreter thinks the blank line signals the end of the for loop’s block.

IPython has a magic function called %paste, which correctly pastes whatever is on your clipboard, whitespace and all. This alone is a good reason to use IPython.

Functions

A function is a rule for taking zero or more inputs and returning a corresponding output. In Python, we typically define functions using def:

def double(x):
    """
    This is where you put an optional docstring that explains what the
    function does. For example, this function multiplies its input by 2.
    """
    return x * 2

Python functions are first-class, which means that we can assign them to variables and pass them into functions just like any other arguments:

def apply_to_one(f):
    """Calls the function f with 1 as its argument"""
    return f(1)

my_double = double             # refers to the previously defined function
x = apply_to_one(my_double)    # equals 2

It is also easy to create short anonymous functions, or lambdas:

y = apply_to_one(lambda x: x + 4)      # equals 5

You can assign lambdas to variables, although most people will tell you that you should just use def instead:

another_double = lambda x: 2 * x       # don't do this

def another_double(x):
    """Do this instead"""
    return 2 * x

Function parameters can also be given default arguments, which only need to be specified when you want a value other than the default:

def my_print(message = "my default message"):
    print(message)

my_print("hello")   # prints 'hello'
my_print()          # prints 'my default message'

It is sometimes useful to specify arguments by name:

def full_name(first = "What's-his-name", last = "Something"):
    return first + " " + last

full_name("Joel", "Grus")     # "Joel Grus"
full_name("Joel")             # "Joel Something"
full_name(last="Grus")        # "What's-his-name Grus"

We will be creating many, many functions.

Lists

Probably the most fundamental data structure in Python is the list, which is simply an ordered collection (it is similar to what in other languages might be called an array, but with some added functionality):

integer_list = [1, 2, 3]
heterogeneous_list = ["string", 0.1, True]
list_of_lists = [integer_list, heterogeneous_list, []]

list_length = len(integer_list)     # equals 3
list_sum    = sum(integer_list)     # equals 6

You can get or set the nth element of a list with square brackets:

x = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

zero = x[0]          # equals 0, lists are 0-indexed
one = x[1]           # equals 1
nine = x[-1]         # equals 9, 'Pythonic' for last element
eight = x[-2]        # equals 8, 'Pythonic' for next-to-last element
x[0] = -1            # now x is [-1, 1, 2, 3, ..., 9]

You can also use square brackets to slice lists. The slice i:j means all elements from i (inclusive) to j (not inclusive). If you leave off the start of the slice, you’ll slice from the beginning of the list, and if you leave of the end of the slice, you’ll slice until the end of the list:

first_three = x[:3]                 # [-1, 1, 2]
three_to_end = x[3:]                # [3, 4, ..., 9]
one_to_four = x[1:5]                # [1, 2, 3, 4]
last_three = x[-3:]                 # [7, 8, 9]
without_first_and_last = x[1:-1]    # [1, 2, ..., 8]
copy_of_x = x[:]                    # [-1, 1, 2, ..., 9]

You can similarly slice strings and other “sequential” types.

A slice can take a third argument to indicate its stride, which can be negative:

every_third = x[::3]                 # [-1, 3, 6, 9]
five_to_three = x[5:2:-1]            # [5, 4, 3]

Python has an in operator to check for list membership:

1 in [1, 2, 3]    # True
0 in [1, 2, 3]    # False

This check involves examining the elements of the list one at a time, which means that you probably shouldn’t use it unless you know your list is pretty small (or unless you don’t care how long the check takes).

It is easy to concatenate lists together. If you want to modify a list in place, you can use extend to add items from another collection:

x = [1, 2, 3]
x.extend([4, 5, 6])     # x is now [1, 2, 3, 4, 5, 6]

If you don’t want to modify x, you can use list addition:

x = [1, 2, 3]
y = x + [4, 5, 6]       # y is [1, 2, 3, 4, 5, 6]; x is unchanged

More frequently we will append to lists one item at a time:

x = [1, 2, 3]
x.append(0)      # x is now [1, 2, 3, 0]
y = x[-1]        # equals 0
z = len(x)       # equals 4

It’s often convenient to unpack lists when you know how many elements they contain:

x, y = [1, 2]    # now x is 1, y is 2

although you will get a ValueError if you don’t have the same number of elements on both sides.

A common idiom is to use an underscore for a value you’re going to throw away:

_, y = [1, 2]    # now y == 2, didn't care about the first element

Dictionaries

Another fundamental data structure is a dictionary, which associates values with keys and allows you to quickly retrieve the value corresponding to a given key:

empty_dict = {}                     # Pythonic
empty_dict2 = dict()                # less Pythonic
grades = {"Joel": 80, "Tim": 95}    # dictionary literal

You can look up the value for a key using square brackets:

joels_grade = grades["Joel"]        # equals 80

But you’ll get a KeyError if you ask for a key that’s not in the dictionary:

try:
    kates_grade = grades["Kate"]
except KeyError:
    print("no grade for Kate!")

You can check for the existence of a key using in:

joel_has_grade = "Joel" in grades     # True
kate_has_grade = "Kate" in grades     # False

This membership check is fast even for large dictionaries.

Dictionaries have a get method that returns a default value (instead of raising an exception) when you look up a key that’s not in the dictionary:

joels_grade = grades.get("Joel", 0)   # equals 80
kates_grade = grades.get("Kate", 0)   # equals 0
no_ones_grade = grades.get("No One")  # default is None

You can assign key/value pairs using the same square brackets:

grades["Tim"] = 99                    # replaces the old value
grades["Kate"] = 100                  # adds a third entry
num_students = len(grades)            # equals 3

As you saw in Chapter 1, you can use dictionaries to represent structured data:

tweet = {
    "user" : "joelgrus",
    "text" : "Data Science is Awesome",
    "retweet_count" : 100,
    "hashtags" : ["#data", "#science", "#datascience", "#awesome", "#yolo"]
}

although we’ll soon see a better approach.

Besides looking for specific keys, we can look at all of them:

tweet_keys   = tweet.keys()     # iterable for the keys
tweet_values = tweet.values()   # iterable for the values
tweet_items  = tweet.items()    # iterable for the (key, value) tuples

"user" in tweet_keys            # True, but not Pythonic
"user" in tweet                 # Pythonic way of checking for keys
"joelgrus" in tweet_values      # True (slow but the only way to check)

Dictionary keys must be “hashable”; in particular, you cannot use lists as keys. If you need a multipart key, you should probably use a tuple or figure out a way to turn the key into a string.

defaultdict

Imagine that you’re trying to count the words in a document. An obvious approach is to create a dictionary in which the keys are words and the values are counts. As you check each word, you can increment its count if it’s already in the dictionary and add it to the dictionary if it’s not:

word_counts = {}
for word in document:
    if word in word_counts:
        word_counts[word] += 1
    else:
        word_counts[word] = 1

You could also use the “forgiveness is better than permission” approach and just handle the exception from trying to look up a missing key:

word_counts = {}
for word in document:
    try:
        word_counts[word] += 1
    except KeyError:
        word_counts[word] = 1

A third approach is to use get, which behaves gracefully for missing keys:

word_counts = {}
for word in document:
    previous_count = word_counts.get(word, 0)
    word_counts[word] = previous_count + 1

Every one of these is slightly unwieldy, which is why defaultdict is useful. A defaultdict is like a regular dictionary, except that when you try to look up a key it doesn’t contain, it first adds a value for it using a zero-argument function you provided when you created it. In order to use defaultdicts, you have to import them from collections:

from collections import defaultdict

word_counts = defaultdict(int)          # int() produces 0
for word in document:
    word_counts[word] += 1

They can also be useful with list or dict, or even your own functions:

dd_list = defaultdict(list)             # list() produces an empty list
dd_list[2].append(1)                    # now dd_list contains {2: [1]}

dd_dict = defaultdict(dict)             # dict() produces an empty dict
dd_dict["Joel"]["City"] = "Seattle"     # {"Joel" : {"City": Seattle"}}

dd_pair = defaultdict(lambda: [0, 0])
dd_pair[2][1] = 1                       # now dd_pair contains {2: [0, 1]}

These will be useful when we’re using dictionaries to “collect” results by some key and don’t want to have to check every time to see if the key exists yet.

Truthiness

Booleans in Python work as in most other languages, except that they’re capitalized:

one_is_less_than_two = 1 < 2          # equals True
true_equals_false = True == False     # equals False

Python uses the value None to indicate a nonexistent value. It is similar to other languages’ null:

x = None
assert x == None, "this is the not the Pythonic way to check for None"
assert x is None, "this is the Pythonic way to check for None"

Python lets you use any value where it expects a Boolean. The following are all “falsy”:

  • False

  • None

  • [] (an empty list)

  • {} (an empty dict)

  • ""

  • set()

  • 0

  • 0.0

Pretty much anything else gets treated as True. This allows you to easily use if statements to test for empty lists, empty strings, empty dictionaries, and so on. It also sometimes causes tricky bugs if you’re not expecting this behavior:

s = some_function_that_returns_a_string()
if s:
    first_char = s[0]
else:
    first_char = ""

A shorter (but possibly more confusing) way of doing the same is:

first_char = s and s[0]

since and returns its second value when the first is “truthy,” and the first value when it’s not. Similarly, if x is either a number or possibly None:

safe_x = x or 0

is definitely a number, although:

safe_x = x if x is not None else 0

is possibly more readable.

Python has an all function, which takes an iterable and returns True precisely when every element is truthy, and an any function, which returns True when at least one element is truthy:

all([True, 1, {3}])   # True, all are truthy
all([True, 1, {}])    # False, {} is falsy
any([True, 1, {}])    # True, True is truthy
all([])               # True, no falsy elements in the list
any([])               # False, no truthy elements in the list

Automated Testing and assert

As data scientists, we’ll be writing a lot of code. How can we be confident our code is correct? One way is with types (discussed shortly), but another way is with automated tests.

There are elaborate frameworks for writing and running tests, but in this book we’ll restrict ourselves to using assert statements, which will cause your code to raise an AssertionError if your specified condition is not truthy:

assert 1 + 1 == 2
assert 1 + 1 == 2, "1 + 1 should equal 2 but didn't"

As you can see in the second case, you can optionally add a message to be printed if the assertion fails.

It’s not particularly interesting to assert that 1 + 1 = 2. What’s more interesting is to assert that functions you write are doing what you expect them to:

def smallest_item(xs):
    return min(xs)

assert smallest_item([10, 20, 5, 40]) == 5
assert smallest_item([1, 0, -1, 2]) == -1

Throughout the book we’ll be using assert in this way. It is a good practice, and I strongly encourage you to make liberal use of it in your own code. (If you look at the book’s code on GitHub, you will see that it contains many, many more assert statements than are printed in the book. This helps me be confident that the code I’ve written for you is correct.)

Another less common use is to assert things about inputs to functions:

def smallest_item(xs):
    assert xs, "empty list has no smallest item"
    return min(xs)

We’ll occasionally do this, but more often we’ll use assert to check that our code is correct.

Object-Oriented Programming

Like many languages, Python allows you to define classes that encapsulate data and the functions that operate on them. We’ll use them sometimes to make our code cleaner and simpler. It’s probably simplest to explain them by constructing a heavily annotated example.

Here we’ll construct a class representing a “counting clicker,” the sort that is used at the door to track how many people have shown up for the “advanced topics in data science” meetup.

It maintains a count, can be clicked to increment the count, allows you to read_count, and can be reset back to zero. (In real life one of these rolls over from 9999 to 0000, but we won’t bother with that.)

To define a class, you use the class keyword and a PascalCase name:

class CountingClicker:
    """A class can/should have a docstring, just like a function"""

A class contains zero or more member functions. By convention, each takes a first parameter, self, that refers to the particular class instance.

Normally, a class has a constructor, named __init__. It takes whatever parameters you need to construct an instance of your class and does whatever setup you need:

    def __init__(self, count = 0):
        self.count = count

Although the constructor has a funny name, we construct instances of the clicker using just the class name:

clicker1 = CountingClicker()           # initialized to 0
clicker2 = CountingClicker(100)        # starts with count=100
clicker3 = CountingClicker(count=100)  # more explicit way of doing the same

Notice that the __init__ method name starts and ends with double underscores. These “magic” methods are sometimes called “dunder” methods (double-UNDERscore, get it?) and represent “special” behaviors.

Note

Class methods whose names start with an underscore are—by convention—considered “private,” and users of the class are not supposed to directly call them. However, Python will not stop users from calling them.

Another such method is __repr__, which produces the string representation of a class instance:

    def __repr__(self):
        return f"CountingClicker(count={self.count})"

And finally we need to implement the public API of our class:

    def click(self, num_times = 1):
        """Click the clicker some number of times."""
        self.count += num_times

    def read(self):
        return self.count

    def reset(self):
        self.count = 0

Having defined it, let’s use assert to write some test cases for our clicker:

clicker = CountingClicker()
assert clicker.read() == 0, "clicker should start with count 0"
clicker.click()
clicker.click()
assert clicker.read() == 2, "after two clicks, clicker should have count 2"
clicker.reset()
assert clicker.read() == 0, "after reset, clicker should be back to 0"

Writing tests like these help us be confident that our code is working the way it’s designed to, and that it remains doing so whenever we make changes to it.

We’ll also occasionally create subclasses that inherit some of their functionality from a parent class. For example, we could create a non-reset-able clicker by using CountingClicker as the base class and overriding the reset method to do nothing:

# A subclass inherits all the behavior of its parent class.
class NoResetClicker(CountingClicker):
    # This class has all the same methods as CountingClicker

    # Except that it has a reset method that does nothing.
    def reset(self):
        pass

clicker2 = NoResetClicker()
assert clicker2.read() == 0
clicker2.click()
assert clicker2.read() == 1
clicker2.reset()
assert clicker2.read() == 1, "reset shouldn't do anything"

Iterables and Generators

One nice thing about a list is that you can retrieve specific elements by their indices. But you don’t always need this! A list of a billion numbers takes up a lot of memory. If you only want the elements one at a time, there’s no good reason to keep them all around. If you only end up needing the first several elements, generating the entire billion is hugely wasteful.

Often all we need is to iterate over the collection using for and in. In this case we can create generators, which can be iterated over just like lists but generate their values lazily on demand.

One way to create generators is with functions and the yield operator:

def generate_range(n):
    i = 0
    while i < n:
        yield i   # every call to yield produces a value of the generator
        i += 1

The following loop will consume the yielded values one at a time until none are left:

for i in generate_range(10):
    print(f"i: {i}")

(In fact, range is itself lazy, so there’s no point in doing this.)

With a generator, you can even create an infinite sequence:

def natural_numbers():
    """returns 1, 2, 3, ..."""
    n = 1
    while True:
        yield n
        n += 1

although you probably shouldn’t iterate over it without using some kind of break logic.

Tip

The flip side of laziness is that you can only iterate through a generator once. If you need to iterate through something multiple times, you’ll need to either re-create the generator each time or use a list. If generating the values is expensive, that might be a good reason to use a list instead.

A second way to create generators is by using for comprehensions wrapped in parentheses:

evens_below_20 = (i for i in generate_range(20) if i % 2 == 0)

Such a “generator comprehension” doesn’t do any work until you iterate over it (using for or next). We can use this to build up elaborate data-processing pipelines:

# None of these computations *does* anything until we iterate
data = natural_numbers()
evens = (x for x in data if x % 2 == 0)
even_squares = (x ** 2 for x in evens)
even_squares_ending_in_six = (x for x in even_squares if x % 10 == 6)
# and so on

Not infrequently, when we’re iterating over a list or a generator we’ll want not just the values but also their indices. For this common case Python provides an enumerate function, which turns values into pairs (index, value):

names = ["Alice", "Bob", "Charlie", "Debbie"]

# not Pythonic
for i in range(len(names)):
    print(f"name {i} is {names[i]}")

# also not Pythonic
i = 0
for name in names:
    print(f"name {i} is {names[i]}")
    i += 1

# Pythonic
for i, name in enumerate(names):
    print(f"name {i} is {name}")

We’ll use this a lot.

Randomness

As we learn data science, we will frequently need to generate random numbers, which we can do with the random module:

import random
random.seed(10)  # this ensures we get the same results every time

four_uniform_randoms = [random.random() for _ in range(4)]

# [0.5714025946899135,       # random.random() produces numbers
#  0.4288890546751146,       # uniformly between 0 and 1.
#  0.5780913011344704,       # It's the random function we'll use
#  0.20609823213950174]      # most often.

The random module actually produces pseudorandom (that is, deterministic) numbers based on an internal state that you can set with random.seed if you want to get reproducible results:

random.seed(10)         # set the seed to 10
print(random.random())  # 0.57140259469
random.seed(10)         # reset the seed to 10
print(random.random())  # 0.57140259469 again

We’ll sometimes use random.randrange, which takes either one or two arguments and returns an element chosen randomly from the corresponding range:

random.randrange(10)    # choose randomly from range(10) = [0, 1, ..., 9]
random.randrange(3, 6)  # choose randomly from range(3, 6) = [3, 4, 5]

There are a few more methods that we’ll sometimes find convenient. For example, random.shuffle randomly reorders the elements of a list:

up_to_ten = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
random.shuffle(up_to_ten)
print(up_to_ten)
# [7, 2, 6, 8, 9, 4, 10, 1, 3, 5]   (your results will probably be different)

If you need to randomly pick one element from a list, you can use random.choice:

my_best_friend = random.choice(["Alice", "Bob", "Charlie"])     # "Bob" for me

And if you need to randomly choose a sample of elements without replacement (i.e., with no duplicates), you can use random.sample:

lottery_numbers = range(60)
winning_numbers = random.sample(lottery_numbers, 6)  # [16, 36, 10, 6, 25, 9]

To choose a sample of elements with replacement (i.e., allowing duplicates), you can just make multiple calls to random.choice:

four_with_replacement = [random.choice(range(10)) for _ in range(4)]
print(four_with_replacement)  # [9, 4, 4, 2]

args and kwargs

Let’s say we want to create a higher-order function that takes as input some function f and returns a new function that for any input returns twice the value of f:

def doubler(f):
    # Here we define a new function that keeps a reference to f
    def g(x):
        return 2 * f(x)

    # And return that new function
    return g

This works in some cases:

def f1(x):
    return x + 1

g = doubler(f1)
assert g(3) == 8,  "(3 + 1) * 2 should equal 8"
assert g(-1) == 0, "(-1 + 1) * 2 should equal 0"

However, it doesn’t work with functions that take more than a single argument:

def f2(x, y):
    return x + y

g = doubler(f2)
try:
    g(1, 2)
except TypeError:
    print("as defined, g only takes one argument")

What we need is a way to specify a function that takes arbitrary arguments. We can do this with argument unpacking and a little bit of magic:

def magic(*args, **kwargs):
    print("unnamed args:", args)
    print("keyword args:", kwargs)

magic(1, 2, key="word", key2="word2")

# prints
#  unnamed args: (1, 2)
#  keyword args: {'key': 'word', 'key2': 'word2'}

That is, when we define a function like this, args is a tuple of its unnamed arguments and kwargs is a dict of its named arguments. It works the other way too, if you want to use a list (or tuple) and dict to supply arguments to a function:

def other_way_magic(x, y, z):
    return x + y + z

x_y_list = [1, 2]
z_dict = {"z": 3}
assert other_way_magic(*x_y_list, **z_dict) == 6, "1 + 2 + 3 should be 6"

You could do all sorts of strange tricks with this; we will only use it to produce higher-order functions whose inputs can accept arbitrary arguments:

def doubler_correct(f):
    """works no matter what kind of inputs f expects"""
    def g(*args, **kwargs):
        """whatever arguments g is supplied, pass them through to f"""
        return 2 * f(*args, **kwargs)
    return g

g = doubler_correct(f2)
assert g(1, 2) == 6, "doubler should work now"

As a general rule, your code will be more correct and more readable if you are explicit about what sorts of arguments your functions require; accordingly, we will use args and kwargs only when we have no other option.

Type Annotations

Python is a dynamically typed language. That means that it in general it doesn’t care about the types of objects we use, as long as we use them in valid ways:

def add(a, b):
    return a + b

assert add(10, 5) == 15,                  "+ is valid for numbers"
assert add([1, 2], [3]) == [1, 2, 3],     "+ is valid for lists"
assert add("hi ", "there") == "hi there", "+ is valid for strings"

try:
    add(10, "five")
except TypeError:
    print("cannot add an int to a string")

whereas in a statically typed language our functions and objects would have specific types:

def add(a: int, b: int) -> int:
    return a + b

add(10, 5)           # you'd like this to be OK
add("hi ", "there")  # you'd like this to be not OK

In fact, recent versions of Python do (sort of) have this functionality. The preceding version of add with the int type annotations is valid Python 3.6!

However, these type annotations don’t actually do anything. You can still use the annotated add function to add strings, and the call to add(10, "five") will still raise the exact same TypeError.

That said, there are still (at least) four good reasons to use type annotations in your Python code:
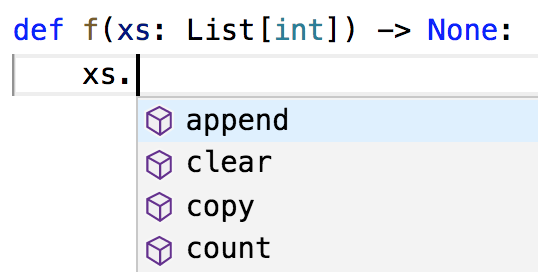
VSCode, but likely your editor does the same.
Figure 2-1. VSCode, but likely your editor does the same

Sometimes people insist that type hints may be valuable on large projects but are not worth the time for small ones. However, since type hints take almost no additional time to type and allow your editor to save you time, I maintain that they actually allow you to write code more quickly, even for small projects.

For all these reasons, all of the code in the remainder of the book will use type annotations. I expect that some readers will be put off by the use of type annotations; however, I suspect by the end of the book they will have changed their minds.

How to Write Type Annotations

As we’ve seen, for built-in types like int and bool and float, you just use the type itself as the annotation. What if you had (say) a list?

def total(xs: list) -> float:
    return sum(total)

This isn’t wrong, but the type is not specific enough. It’s clear we really want xs to be a list of floats, not (say) a list of strings.

The typing module provides a number of parameterized types that we can use to do just this:

from typing import List  # note capital L

def total(xs: List[float]) -> float:
    return sum(total)

Up until now we’ve only specified annotations for function parameters and return types. For variables themselves it’s usually obvious what the type is:

# This is how to type-annotate variables when you define them.
# But this is unnecessary; it's "obvious" x is an int.
x: int = 5

However, sometimes it’s not obvious:

values = []         # what's my type?
best_so_far = None  # what's my type?

In such cases we will supply inline type hints:

from typing import Optional

values: List[int] = []
best_so_far: Optional[float] = None  # allowed to be either a float or None

The typing module contains many other types, only a few of which we’ll ever use:

# the type annotations in this snippet are all unnecessary
from typing import Dict, Iterable, Tuple

# keys are strings, values are ints
counts: Dict[str, int] = {'data': 1, 'science': 2}

# lists and generators are both iterable
if lazy:
    evens: Iterable[int] = (x for x in range(10) if x % 2 == 0)
else:
    evens = [0, 2, 4, 6, 8]

# tuples specify a type for each element
triple: Tuple[int, float, int] = (10, 2.3, 5)

Finally, since Python has first-class functions, we need a type to represent those as well. Here’s a pretty contrived example:

from typing import Callable

# The type hint says that repeater is a function that takes
# two arguments, a string and an int, and returns a string.
def twice(repeater: Callable[[str, int], str], s: str) -> str:
    return repeater(s, 2)

def comma_repeater(s: str, n: int) -> str:
    n_copies = [s for _ in range(n)]
    return ', '.join(n_copies)

assert twice(comma_repeater, "type hints") == "type hints, type hints"

As type annotations are just Python objects, we can assign them to variables to make them easier to refer to:

Number = int
Numbers = List[Number]

def total(xs: Numbers) -> Number:
    return sum(xs)

By the time you get to the end of the book, you’ll be quite familiar with reading and writing type annotations, and I hope you’ll use them in your code.

Welcome to DataSciencester!

This concludes new employee orientation. Oh, and also: try not to embezzle anything.