Das magische Quadrat

Hier kommt noch ein cooles Projekt zum Abschluss dieses Kapitels: das magische Quadrat.

Kennst du magische Quadrate? Das sind Quadrate, die zum Beispiel aus 16 Feldern (4 × 4) bestehen, und in jedem Feld steht eine Zahl. Die Summe der Zahlen jeder Reihe, waagerecht, senkrecht und diagonal, ist dabei genau gleich. Und ebenfalls die Summe der 2×2-Quadrate im Innern des magischen Quadrats. Sowie die Summe der vier Ecken.

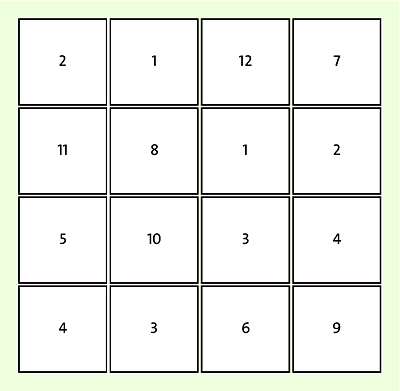
Hier ist ein Beispiel:

Abbildung 7.7    Einfaches magisches Quadrat mit der Summe 22

Addierst du die Reihen, ist die Summe immer 22, ebenso bei allen Spalten, ebenso bei den beiden Diagonalen. Ebenso bei den vier Viererquadraten, aus denen sich das Ganze zusammensetzt, und sogar beim Mittelquadrat. Auch wenn du die vier Ecken addierst, kommt 22 raus. Insgesamt erhältst du beim Zusammenzählen 18 Mal auf verschiedene Weise die Summe 22. Magisch, oder?

Wenn wir jetzt möchten, dass Python uns so ein Quadrat erstellt – mit änderbaren anderen Zahlen als das abgebildete – was brauchen wir dann dafür? Klar, eine Formel, mit der man die einzelnen Zahlen des magischen Quadrats errechnen kann. Formeln kann man nachschlagen – mit Google findet man fast alles. Wir müssen sie uns also nicht selbst ausdenken, wir müssen sie nur in unserem Programm richtig anwenden.

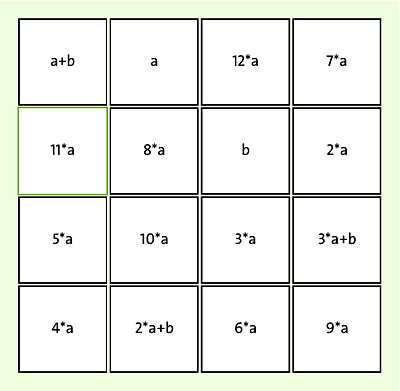
Das Erstellen eines magischen Quadrats funktioniert so: Wir legen zwei ganze Zahlen fest, die wir a und b nennen. Egal welche, beide müssen mindestens 1 sein oder höher. Nun können wir die Inhalte des Quadrats mit der folgenden Formel berechnen, und schon klappt es mit der Magie:

Abbildung 7.8    Das sind die Berechnungsformeln für jede Zelle des magischen Quadrats. a und b sind dabei beliebige ganze Zahlen über 0.

Und noch eine Formel gibt es dazu: Nachdem man die Zahlen a und b festgelegt hat, ergibt sich die magische Summe aller Reihen mit der Berechnung 21 * a + b.

Mehr müssen wir nicht wissen. Wir können jetzt ein Programm schreiben, das uns, nachdem wir a und b festgelegt haben, alle 16 Zahlen des dazu berechneten magischen Quadrates ausgibt, in vier Reihen. Das Abtippen lohnt sich:

a = input("Gib einen Wert für a ein:")
b = input("Gib einen Wert für b ein:")
print "Die Summe aller Reihen, Spalten und Quadrate ist:",a*21+b
# Magisches Quadrat ausgeben:
print "------------------------------------------------------------"
print a+b,a,12*a,7*a
print 11*a,8*a,b,2*a
print 5*a,10*a,3*a,3*a+b
print 4*a,2*a+b,6*a,9*a
print "------------------------------------------------------------"

Erst wird also a eingegeben (eine beliebige Zahl), dann b (ebenfalls beliebig), dann errechnet Python erst einmal die magische Summe (mit der Formel a * 21 + b) und gibt sie aus, danach berechnet es nach unserer Formelvorgabe alle Zahlen für alle Kästchen und gibt sie in vier Reihen aus. Die ausgegebenen Striche dienen nur der Übersicht bei der Ausgabe und kennzeichnen den Anfang und das Ende der Zahlen.

[+]  Kommentare im Code mit »#«

Die vierte Zeile im Code hier ist übrigens eine Kommentarzeile: Du kannst in jedes Python-Programm jederzeit Kommentare einfügen, als eigene Zeile oder direkt nach einem Befehl. Sie beginnen immer mit einem #-Zeichen und enden am Ende der Zeile. Kommentare werden bei der Ausführung des Programms ignoriert. Sie dienen nur dazu, Erläuterungen und Anmerkungen ins Programm einzufügen.

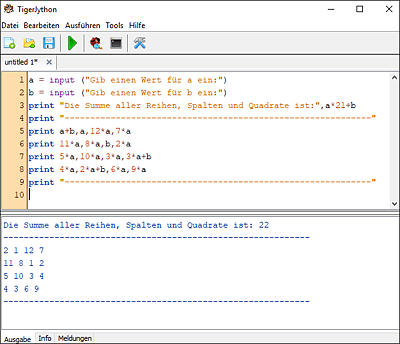
Probiere es erst mal mit den Zahlen 1 und 1 für a und b aus – dann sollte genau das magische Quadrat, das weiter oben abgebildet ist, herauskommen, mit der Summe 22. Wenn nicht, dann ist irgendwo ein Fehler in deinem Programm.

Abbildung 7.9    Das einfachste magische Quadrat (a=1, b=1) sollte so ausgegeben werden.

Jetzt kannst du beliebige Werte testen. Die Zahlen können hoch werden, und du kannst es im Kopf vielleicht gar nicht mehr nachrechnen – aber wenn das Programm korrekt eingegeben wurde, kannst du sicher sein, dass das magische Quadrat funktioniert.