Würfeln ohne Ende

Das können wir am nächsten Beispiel dann noch deutlicher sehen. Bis 100 zählen ist zwar lustig, aber es macht keinen richtigen Sinn. Wie wäre es, wenn wir stattdessen 100 Mal würfeln und am Schluss sehen, was der Durchschnitt der gewürfelten Zahl ist.

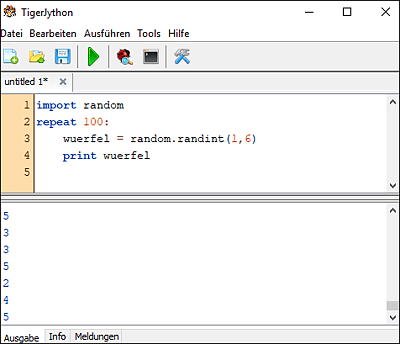
Hundertmal Würfeln ist erst mal kein Problem, denke ich. Nicht vergessen, das random-Modul am Anfang zu importieren, dann geht es los:

Gut, das Ergebnis ist wie erwartet. 100 zufällige Würfelzahlen erscheinen untereinander.

Abbildung 10.2    Hundert Mal Würfeln ist kein Problem.

Um jetzt den Durchschnitt aller Würfe zu ermitteln, musst du natürlich erst einmal alle Würfelzahlen zusammenaddieren. Dazu brauchst du eine Variable für die Summe. Nenne sie am besten einfach summe. Die Anzahl der Würfe kann sich ändern, denn wir können ja mehrere Experimente mit verschiedenen Anzahlen machen. Also sollte die Anzahl auch in eine Variable, die zu Beginn eingegeben wird. Nenne diese Variable einfach anzahl.

Wie sieht das Programm dann aus? Versuche mal, das Würfelprogramm selbst abzuändern: Zuerst wird die Anzahl der Würfe eingegeben und in der Variable anzahl gespeichert, außerdem muss die Variable summe erzeugt und zu Beginn auf 0 gesetzt werden. Dann wird anzahl Male gewürfelt, dabei wird jede Würfelzahl zur Summe addiert, dann wird der Durchschnittswert ermittelt. Durchschnitt? Klar: Das ist die summe geteilt durch die anzahl.

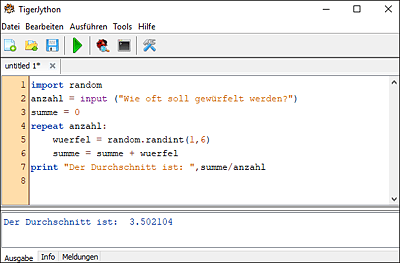
So könnte es aussehen:

import random
anzahl = input("Wie oft soll gewürfelt werden?")
summe = 0
repeat anzahl:
    wuerfel = random.randint(1,6)
    print wuerfel
    summe = summe + wuerfel
print "Der Durchschnitt ist:" , summe / anzahl

Weil wir Zufallszahlen brauchen, wird also zuerst das random-Modul importiert, dann wird die anzahl eingegeben und die summe auf 0 gesetzt. Anschließend wird so oft wie in anzahl eingegeben gewürfelt – das heißt, es wird eine Würfelzahl ermittelt, sie wird zur summe addiert und mit print im Fenster ausgegeben.

Am Schluss wird der Durchschnittswert mit summe / anzahl berechnet und ausgegeben.

Du kannst jetzt verschiedene Anzahlen ausprobieren. Würfelst du nur 5 oder vielleicht 10 Mal, dann schwankt der Durchschnitt noch ziemlich hin und her und kann theoretisch alles zwischen 1 und 6 sein. Je höher die Anzahl der Würfe, desto genauer wird aber der Durchschnittswert.

[+]  Erwartungswert

Wer Wahrscheinlichkeitsrechnung kennt, kann leicht ausrechnen, dass sich der erwartete Durchschnitt bei gleichmäßiger Verteilung der Würfe mit zunehmender Anzahl immer mehr der Zahl 3,5 annähern sollte. Das ist nämlich die genaue Mitte zwischen 1 und 6, und wenn die Zahlen regelmäßig genug verteilt sind, sollte bei Anzahlen über 1.000 in der Regel etwas herauskommen, das sehr nah an der 3,5 liegt.

Bei hohen Anzahlen nervt es dich vielleicht, dass immer jede Würfelzahl im Ausgabefenster angezeigt wird, was eine ganze Weile dauert. Du kannst das verhindern, indem du einfach den Befehl print wuerfel löschst. Jetzt zeigt sich die wahre Rechengeschwindigkeit von Python: Selbst eine Million Würfe (das ist eine 1 mit sechs Nullen) sind in wenigen Sekunden durch und ausgewertet. Wenn man drüber nachdenkt, ist es schon ziemlich erstaunlich, was das Programm da in etwa drei Sekunden leistet.

Abbildung 10.3    Nach einer Million Würfen ist der Durchschnitt sehr nah an der 3,5.

Fazit: Das Ergebnis ist jedes Mal etwas anders, aber es nähert sich immer mehr der Zahl 3,5 an, je öfter gewürfelt wird. Damit verhält sich der Zufallsgenerator aus dem random-Modul genau so wie ein echter idealer Würfel. Gut zu wissen!

Das kann man übrigens auch noch anschaulicher machen. Wie wäre es, wenn das Programm zehn Mal nacheinander 1.000 Würfe macht und die Durchschnitte immer dazu ausgibt, sodass wir zehn Durchschnittswerte untereinander erhalten, die wir vergleichen können? Wie müssen wir das Programm dazu ändern?