Das Probeverfahren

Was muss das Programm machen? Vereinfacht gesagt muss es versuchen, die eingegebene Zahl durch alle Zahlen außer der 1 und sich selbst zu teilen, und prüfen, ob das Ergebnis eine ganze Zahl ist. Wenn das auch nur einmal der Fall ist, ist die Zahl keine Primzahl.

Fangen wir also ganz einfach an. Später wirst du das Programm noch verfeinern und optimieren.

Als Erstes wird die Zahl x eingegeben.

x = input("Gib eine Zahl ein")

Zum Prüfen der Teiler musst du natürlich wieder eine Schleife verwenden. Die Schleife geht alle denkbaren Teiler durch und wird beendet, wenn entweder alle Teiler ohne Ergebnis geprüft wurden – oder wenn ein Teiler »aufgeht«, dann ist es nämlich keine Primzahl.

Wie prüft man nun, ob eine Zahl durch einen Teiler teilbar ist? »Teilbar« ist ja eigentlich jede Zahl, nur eben nicht mit Ganzzahl-Ergebnis. Und das musst du prüfen. Ist das Ergebnis x / teiler eine ganze Zahl?

Du kannst das mit den Mitteln, die du schon kennst, machen. Erinnere dich an den Anfang des Buches mit dem Rechnen auf der Konsole. Es gibt einen Operator (das %-Zeichen), mit dem man den Rest einer Division ermitteln kann (das nennt man auch Modulo). Wenn der Rest 0 ist, dann ist die Zahl glatt teilbar.

if (x % teiler) == 0:
    primzahl = False

Wenn diese Bedingung zutrifft, dann ist x keine Primzahl, weil sie glatt durch einen der teiler teilbar ist (der Rest der Division ergibt 0). Also wird in dem Fall die Variable primzahl auf den Wert False gesetzt (»nicht wahr«). Zu Beginn muss primzahl natürlich auf True gesetzt werden, denn im Ausgangspunkt vermuten wir, dass jede Zahl eine Primzahl ist, bis der Gegenbeweis gefunden wird. Wenn die Variable nach dem Prüfen aller Teiler noch immer auf True steht, ist die Zahl eine Primzahl; wenn sie auf False steht, ist die Zahl keine Primzahl.

Jetzt zur Schleife. Welche Schleife eignet sich besser – eine Zählschleife oder eine while-Schleife?

Nun, man könnte meinen, eine Zählschleife wäre gut geeignet, denn wir wollen ja einfach alle Zahlen von 2 bis x–1 durchprüfen. Dann könnten wir diese Zahlen einfach per Zähler durchgehen und anschließend sehen, ob primzahl auf False gesetzt wurde.

Ja, das würde funktionieren, aber es wäre sehr ineffizient. Angenommen, wir prüfen die Zahl 999. Gleich bei der zweiten Prüfung käme heraus, dass sie durch 3 teilbar ist (also keine Primzahl). Trotzdem würde das Programm noch 995 weitere Teiler ausprobieren, bevor das Ergebnis angezeigt wird. Das kostet unnötig Zeit, vor allem bei großen Zahlen. Wenn die Zahl auch nur durch einen einzigen Teiler teilbar ist, dann kann die Prüfung sofort beendet werden.

Es läuft also wieder auf eine while-Schleife heraus, die dann beendet wird, wenn entweder alle Teiler geprüft wurden oder wenn primzahl == False ist. Oder positiv ausgedrückt: Die while-Schleife läuft solange, wie der teiler kleiner als die Zahl x und der Wert von primzahl wahr ist. Der Teiler beginnt mit 2, und in der Schleife wird er natürlich immer um 1 erhöht, solange wir noch keinen Teiler gefunden haben.

Damit wird die while-Schleife zur Primzahlprüfung von x so aussehen:

teiler = 2
primzahl = True
while (teiler < x) and (primzahl):
    if (x % teiler) == 0:
        primzahl = False
    else:
        teiler = teiler +1

Am Ende nach der Schleife kann dann das Ergebnis ausgegeben werden. Es ist klar: Wenn die Variable primzahl auf True steht (wahr ist), dann handelt es sich um eine Primzahl. Ansonsten handelt es sich um keine Primzahl, und die Variable teiler ist der Gegenbeweis (der erste Teiler, den das Programm gefunden hat und dann die Schleife beendet hat).

if primzahl:
    print x,"ist eine Primzahl."
else:
    print x,"ist keine Primzahl. Teiler:",teiler

Das gesamte Programm sieht jetzt also so aus und funktioniert:

x = input("Gib eine Zahl ein")
teiler = 2
primzahl = True
while (teiler < x) and (primzahl):
    if (x % teiler) == 0:
        primzahl = False
    else:
        teiler = teiler + 1
if primzahl:
    print x , "ist eine Primzahl."
else:
    print x , "ist keine Primzahl. Teiler:" , teiler

Teste das Programm einmal mit kleineren und dann auch mit größeren Zahlen. Es ist absolut zuverlässig und sagt dir sicher, welche Zahl eine Primzahl ist und welche nicht. Bei Nicht-Primzahlen läuft es auch sehr schnell – klar, wenn eine Zahl durch 2 oder 3 teilbar ist, dann braucht die Schleife ja auch nur ein bis zwei Mal durchlaufen werden, und schon ist das Ergebnis da.

Aber bei echten Primzahlen, die richtig hoch sind, spürt man dann doch, dass es eine ganze Weile dauern kann. Gib zum Beispiel mal »9999083« ein (eine Primzahl). Auf meinem Rechner dauert die Prüfung etwa 5 Sekunden. Die Zahl ist sehr hoch: fast zehn Millionen – und deshalb muss das Programm auch fast zehn Millionen Teiler durchprüfen. Zehn Millionen Divisionen und Überprüfungen, da sind 5 Sekunden Rechenzeit immer noch beeindruckend. Aber: Müssen es denn wirklich so viele Überprüfungen sein? Nein – müssen es nicht.

Wenn man darüber etwas nachdenkt, kommt man vielleicht erst einmal zu dem Ergebnis, dass spätestens bei der Hälfte der Zahl eigentlich Schluss sein müsste, denn wenn das Ergebnis der Division kleiner als 2 ist, kann keine sinnvolle Ganzzahl mehr dabei herauskommen. Denkt man weiter nach, reduziert es sich noch viel mehr. Mathematischer Fakt ist: Schon bei der Wurzel der geprüften Zahl kann man mit der Überprüfung Schluss machen, denn ab da wäre der Teiler so groß wie das Divisionsergebnis, und anschließend dreht es sich nur noch um. Wenn also bis zur Wurzel von x kein Teiler gefunden wurde, wird es auch danach keinen mehr geben. Das macht einen riesigen Unterschied. Bei der Zahl 9.999.083 müsste das Programm dann nicht mehr fast zehn Millionen Rechnungen und Überprüfungen machen, sondern nur noch 3.161. So wird das Programm natürlich extrem viel effizienter und schneller.

Wir legen jetzt also einen Maximalwert fest, bis zu dem der Teiler gehen muss, bevor die Schleife beendet ist. Die Variable nennen wir max, und in ihr ist die Wurzel von x. (Die Wurzel können wir auch ohne das Modul math ermitteln, indem wir x ** 0.5 rechnen.) Die Schleife ändert sich also folgendermaßen:

maximum = x ** 0.5
while (teiler <= maximum) and (primzahl):

Achte darauf, dass in der ersten Klammer jetzt <= steht, denn komplett bis einschließlich zur Wurzel von x sollen alle Teiler durchgeprüft werden. Ändere das Programm und prüfe die Zahl 9.999.083 noch einmal. Merkst du, wie viel schneller es jetzt geht? Da kommt das Ergebnis wieder sofort.

So ist das Programm auf jeden Fall auch für hohe Zahlen schnell und brauchbar – jedenfalls bis zu einer Grenze, die sicherlich für alle normalen Maßstäbe akzeptabel ist.

Es gäbe aber durchaus noch mehr Möglichkeiten, das Programm zu optimieren – zum Beispiel könnte man die Zahl gleich am Anfang darauf überprüfen, ob sie gerade ist (also durch 2 teilbar). Wenn ja, dann ist sie sowieso keine Primzahl, und die Überprüfung braucht gar nicht erst begonnen werden. Wenn nein, dann ist es auf jeden Fall eine ungerade Zahl, und die Variable teiler kann bei 3 beginnen und immer um 2 erhöht werden, denn gerade Teiler brauchen wir nicht zu prüfen – sie können bei einer ungeraden Zahl nicht mehr zutreffen. Wenn du möchtest, kannst du das Programm selbst dahin weiter optimieren. Das würde die Zeit der Überprüfung noch einmal halbieren! Du findest Beispiele für alle Optimierungen auch auf der DVD zum Buch oder auf der Webseite des Buches.

Aufgabe

Zum Schluss der Primzahlenberechnung noch eine Aufgabe für dich:

Angenommen, jemand fragt dich nach einer Liste aller Primzahlen von 1 bis 1.000, damit er darin jederzeit nachschlagen kann. Wie kannst du das Primzahltestprogramm so umbauen, dass es diese Liste aller Primzahlen von 1 bis 1.000 erzeugt?

Versuche, diese Aufgabe selber zu lösen. Du brauchst nicht viel Neues dafür. Anstatt die Zahl x mit input einzugeben, setzt du x am Anfang auf 2 und verwendest dann eine Zählerschleife (repeat), die 999 Mal durchgeht und die Überprüfung macht. Nur wenn die Zahl eine Primzahl ist, wird sie mit print ausgegeben. Am Schluss der Schleife erhöhst du x um 1.

Alles klar?

Hier die Lösung zum Vergleichen:

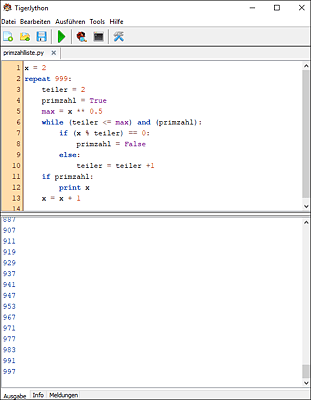
x = 2
repeat 999:
    teiler = 2
    primzahl = True
    maximum = x ** 0.5
    while (teiler <= maximum) and (primzahl):
        if (x % teiler) == 0:
            primzahl = False
        else:
            teiler = teiler +1
    if primzahl:
        print x
    x = x + 1

Abbildung 10.9    Eine Liste aller Primzahlen unter 1.000. In nur einer Sekunde berechnet.