APPENDIX TO CHAPTER TWO
Formal Expression of Aspects of Neighborhood
In this appendix, I define the concepts of congruence, accordance, and generality more formally and precisely in terms of formulae. Start with an individual designated n, with a predetermined set of personal characteristics, who is residing at a particular address. The first dimension of this person’s externality space, individual congruence (Cen), is the degree to which individual n’s perceptual boundaries of the externality space (Yen) for a particular externality (e) correspond to some predetermined geographic boundaries defined by streets, topographical features, or administrative fiat that delineate an unambiguously bordered space (X) containing the property in which the nth individual resides. Formally, I specify the congruence between this individual’s particular externality space and the area under investigation as
(1) Cen = (X ∩ Yen)/(X ∪ Yen)
where ∩ and ∪ signify intersection and union, respectively, in set terminology. Heuristically, X ∩ Yen represents the area of the region where person n’s perceptual map for the impact of externality e overlaps the map of the predetermined area, and X ∪ Yen represents the sum of the nonduplicated areas of X and Y. The value of Cen ranges from a minimum of zero to a maximum of one.
The second dimension that can be specified for an individual, generality, is the degree to which individual n’s externality spaces (Y) correspond across E number of different externalities, with all permutations considered. Formally, individual n’s generality is
(2) 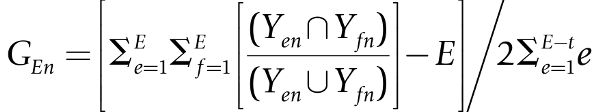
Heuristically, GEn represents the mean ratio of overlapping to footprint areas of externality spaces specified for a variety of potential externalities, for all possible permutations of externality combinations excluding identities (e = f). The value of GEn ranges from a minimum of zero to a maximum of one (which is scaled by dividing the grand sum by 2ΣE–te=1e).
Now consider the three dimensions of neighborhood that one may compute across aggregations of individuals. As above, I begin by taking as given some predetermined geographic area of a city with clearly specified cartographic boundaries: area X. This spatial set will demarcate a particular number (I) of residents who live in X, (J) owners of residential property in X, and (K) others with financial interests in these properties in X, such as real estate brokers or financial institution officers. One may select from this group all or some subset as the basis for analysis. Let this group consist of N members.
Now the aggregate degree of congruence for the space X for an externality e over N members of the group is the summation of individuals’ congruence as defined in equation 1:
(3) 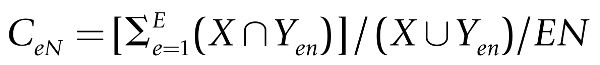
where N = I, J, K, or combinations or subsets thereof. Thus, one can specify aggregate congruence for a particular externality in terms of a group mean of the ratios of overlapping to footprint areas of X versus the members’ externality spaces for externality e. Maximum aggregate congruence is obtained (CeN = 1) when each group member’s perceptual space for the particular externality corresponds to the predetermined geographic area; minimum congruence is obtained (CeN = 0) when there is no correspondence whatever.
If, however, one wished to define an even more aggregated level of congruence, one could easily expand equation 3 to include summations across all individuals in area X and all E externality types:
(4) 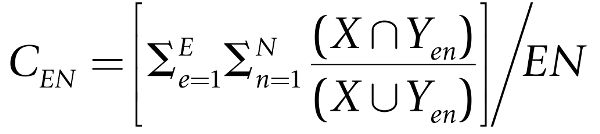
where 0 < CEN < 1 and N = I + J + K.
Moreover, one could in principle expand aggregate congruence further by considering the views of those prospective households, residential and nonresidential property owners, and public and private institutional investors who might consider living or investing in the area being considered. The only modification required in this case would be to use the potential location that each entity was considering moving to or investing in as the point upon which the externality space was defined (e.g., census tract centroid). Having done so, the addition of another summation term in equation 4 involving these M prospective entities is straightforward. Of course, with this aggregation across two types of entities—current and prospective residents and investors—the issue of weighting will arise. Which (if either) group’s perceptions of externality spaces are more important in defining the aggregate congruence of this space? As a practical matter, this issue may not arise, because the analyst is likely to be interested in computing aggregate accordance separately for these two sets of perceivers.
Next, we can consider the second dimension of the aggregate neighborhood—generality, the aggregate degree to which the individuals’ externality spaces coincide for E different externalities, as given by equation 2, summed over N individuals:
(5) 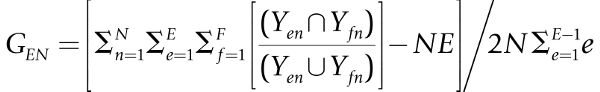
N = I, if residents; J, if owners; K, if others; or combinations of I, J, and K. Aggregate generality is thus the mean of the ratios of overlapping to footprint areas of all possible two-way externality space comparisons, summed over all group members in area X. The generality of area X over a variety of E different externalities would be maximized (GEN = 1) for a particular group in X if each individual in the group were to perceive the same boundaries for all externalities (although these boundaries need not coincide from individual to individual). Generality would be minimized (GEN = 0) if each and every individual’s externality space for any particular externality did not overlap with that for any other externality.
The final aggregate dimension is accordance: the degree to which all N individuals’ externality spaces for a particular externality e overlap. I specified it as
(6) ![]()
where N = I, J, K or combinations thereof; 0 < AeN < 1. Accordance for a particular externality is thus the mean of the ratios of overlapping to footprint areas of all possible two-way interpersonal comparisons of e externality space for N group members in area X.
It should be apparent at this point that CEN, GEN, and AEN as specified are interval measures of three distinct dimensions of the aggregate relationships between externality spaces existing for some predefined geographic area. As such, they are not comparable in a cardinal sense. Certain logical connections do exist among them, of course. For instance, AEN and GEN maximization is a necessary (but not sufficient) condition for CEN to be maximized. In other words, for everyone in an area to agree that its predetermined boundaries accurately reflect their externality space for all externalities, they must also agree that their externality space is the same across all people and all externalities. The converse is not true, however; there may be complete accordance and generality, but the common space thus specified may have little congruence with the predetermined boundaries of the area established by the public sector. Through analogous logic, it can be demonstrated that A and G minimization is neither a necessary nor a sufficient condition for CEN minimization. Finally, AEN and GEN serve as constraints on the maximum CEN level attainable for a particular spatial set X. Although no precise mathematical relationship can be specified at this level of generality, it is intuitively clear that if, for example, AEN and GEN were low, CEN would also tend to be low. That is, if there were little overlap of externality spaces across various individuals and across various externalities, there could not be much consistent overlap between these spaces and area X.