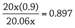
Notes
Introduction
1. Here someone might object that the no-smoking ashtray example does not contain premises and a conclusion, so reasoning is not central to what a paradox is. I’d respond that in the case of the ashtray, the self-flowing flask, and so on, the “facts” related to these items can be turned into statements, and pieces of reasoning be constructed out of them. For example, the ashtray paradox can be put as follows: (1) it is hereby ordered that you not smoke, (2) it is hereby ordered that when you smoke, you use this ashtray, (3) therefore, it is hereby ordered that you smoke (from 2) and not smoke (from 1).
1 A New Way to Think about Paradoxes and Solutions
1. Admittedly, this is not a very deep paradox, given that although it is surprising, there is nothing inconsistent with granting the conclusion, given the assumption.
2. This is, admittedly, a very simplistic account of combined subjective probability, but it works for our purposes. If this were to be fleshed out to account cases in which A and B are dependent on each other, then the combined probability of A and B should be the probability of A multiplied by the probability of B given A (i.e., P(A & B) = P(A) × P(B|A)). In the vast majority of cases, though, a simple multiplication of A and B is fine.
3. See the glossary for a definition of validity. For simplicity, you can think of valid reasoning here as “good” reasoning.
2 How to Solve Paradoxes
1. Usually, another axiom is added that wasn’t original to ZF—the axiom of choice—and the theory is abbreviated ZFC.
2. An axiom schema differs from an axiom in that it contains one or more variables as placeholders for a term of subformula of the language.
3. It is given that A and H entail e, but not-e is observed. Also the probability of observing not-e while A and H are true is 0. That is, P(not-e | A and H) = 0.
We assigned H a very high probability, P (H) = 0.9, whereas we have assigned A a prior probability that makes it only slightly more likely than not: P (A) = 0.6. We also assumed that H and A are statistically independent. That is, the probability of H does not change the probability of A, or vice versa.
With regard to the assumed likelihoods, the probability of not-e being observed, given that A is true and not-H is assumed to be a very small number, x (for example, 0.001). That is, P(not-e | A and not-H) = x. On the other hand, we assumed the likelihood of not-e being observed given not-A being the case is assumed to be 50 times more likely, 50x. So: P(not-e | not-A and not-H) = 50x and P (not-e | not-A and H) = 50x.
We then plug these numbers into a form of Bayes’ theorem:
P(H | not-e) = P(not-e | H) P(H)
P(not-e)
P(not-e) = P(not-e | H) P(H) + P(not-e | not-H) P(not-H)
P(not-e | H) = P(not-e | A and H) P(A) + P(not-e | not-A and H) P(not-A)
= 0 + 50x (0.4)
= 20.6x
P(not-e) = 20x (0.9) + 2.06x = 20.06x.
For the posterior probability of H,
P(H | not-e) = 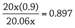
For the posterior probability of A,
P(A | not-e) = P(not-e | A) P (A)
P(not-e)
P(not-e | A) = P(not-e | A and H) P(H) + P(not-e | A and not-H) P(not-H)
= 0 + x (0.1) = 0.1x
P(A | not-e) = 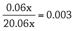
Whereas the probability of H is hardly changed, the probability of A plummets.
4. Here you might notice that the way of determining truth-values for conjunctions in fuzzy logic is different from the simple multiplication used in determining the combined subjective probabilities in our discussion of the paradoxicality rating in chapter 1. According to fuzzy logic, a low truth-value of say, 0.2, when combined with one of say, 0.9, will result in a combined truth value of 0.2, and the subjective probability as we are determining it will be 0.18—only slightly lower. But for 0.4 and 0.5 values, the combined truth-value on fuzzy logic is 0.4, while the combined subjective probability of the two, if these values are taken for degrees of belief, will be 0.2—less than half than that of taking the minimum of the two values. For us, using the straightforward multiplication makes sense because we want a greatly reduced degree of belief for even a little bit of uncertainty. When dealing with degrees of truth, on the other hand, this approach is not necessary, or even desirable.
3 Paradox Lost? On the Successes (and Failures) of Solutions to Paradoxes
1. For Schiffer, a happy-face solution points to a flawed part of the paradox, and then explains why we mistakenly believed that the flaw was acceptable.
2. A discussion of the puzzles associated with comparing infinite sets, for example, was given by Albert of Saxony (1492) in his Questiones subtilissime in libros de cello et mundo.
3. I am not an historian of logic, but I am interested the history of solutions. There are interesting connections to more recent solutions, and these solutions provide inductive grounds for drawing a generalization about solutions to paradoxes. A prime resource I used was Kneale and Kneale 1962.
4. Stephen Read (2002) has a somewhat different, and much fuller, take on this.
5. These theories deal with different types of phenomena and are not, strictly speaking, in conflict. However, one emerged as more prominent than the other.