

Welfare economics
Gérard Debreu (1921–2004)
1874 French economist Léon Walras shows that a competitive, decentralized economy can achieve a stable equilibrium.
1942 Polish economist Oscar Lange provides an early proof of the efficiency of markets.
1967 US economist Herbert Scarf demonstrates a method for applying real-world economic data to general equilibrium models.
1990s New models of the macroeconomy integrate general equilibrium analysis with real-world economic data over time.
By the 1860s and 70s mainstream economics had developed a distinctive set of claims about the world, offering mathematical models that allowed economists to assess individual behavior in certain market conditions. These models were taken from the rapidly developing mathematics that described the natural world. This development, sometimes called a “marginalist revolution,” involved a claim that value is determined by people’s preferences and resources rather than by a more objective or absolute standard, and it allowed pressing theoretical questions to be posed in new ways. Did Adam Smith’s “invisible hand” of the market really guide self-interested individuals to the best available outcomes? Were markets more, or less, efficient than other ways of guiding society? Could completely free markets even exist?
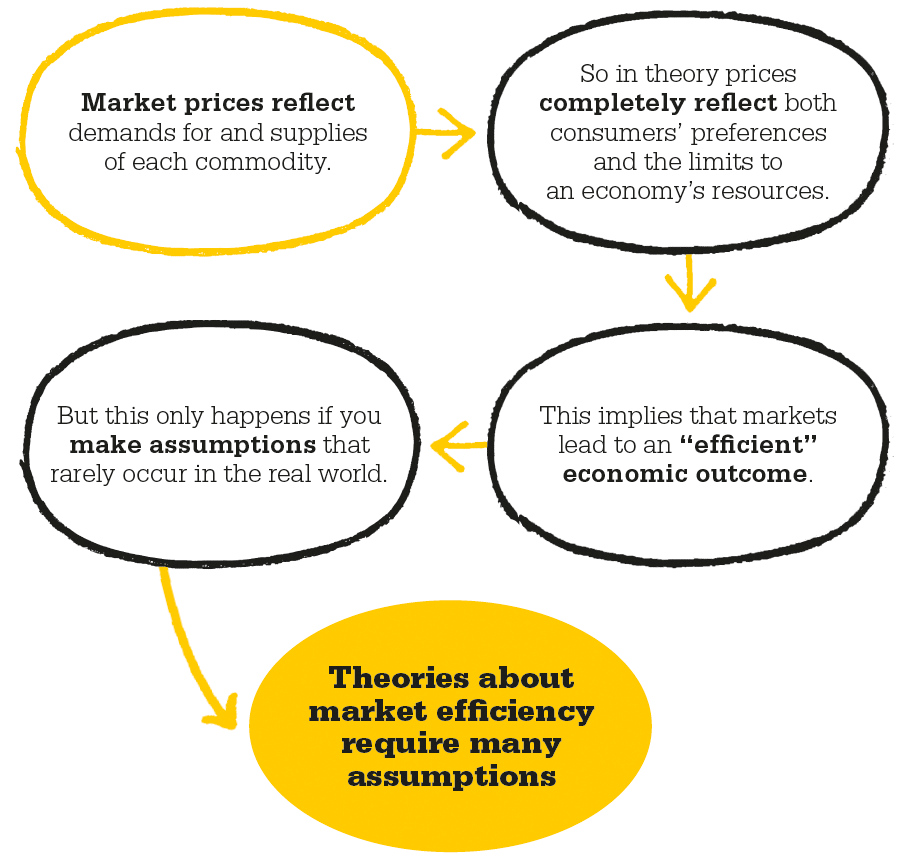
French economist Léon Walras was one of the pioneers of this revolution in theory. He attempted to show that markets, left to their own devices, can achieve a stable outcome for the whole of society, perfectly balancing the demands of consumers and firms with the supply of goods and services. It was known that a single market could achieve this balance, or equilibrium, but it was not clear that a whole set of markets could do the same thing.
"How this coordination [of supply and demand] takes place has been a central preoccupation of economic theory since Adam Smith."
Kenneth Arrow
The problem of “general equilibrium” was rigorously solved in 1954 by French mathematician Gérard Debreu and US economist Kenneth Arrow. Applying advanced mathematics, they showed that under certain circumstances a set of markets could achieve an overall equilibrium. In a sense Arrow and Debreu had reworked Adam Smith’s argument that free markets would lead to social order. But Smith made a stronger claim than the purely factual one that markets tend toward a point of stability. He also said that this equilibrium was desirable because it entailed a free society.

Governments redistribute wealth by taxing goods such as gasoline. Under certain assumptions, it can be shown that the free market adjusts to achieve efficient use of goods despite taxes.
Modern economists measure desirability using a concept known as “Pareto efficiency”. In a Pareto-efficient situation it is impossible to make one person better off without making another person worse off. An improvement takes place in an economy if goods change hands in such a way that at least one person’s welfare increases and no one else’s falls. Arrow and Debreu connected market equilibrium with Pareto efficiency. In doing so they rigorously probed Smith’s ultimate contention that market outcomes are good. They did this by proving two theorems, known as the “fundamental theorems of welfare economics.”
"An allocation of resources could be efficient in a Pareto sense and yet yield enormous riches to some and dire poverty to others."
Kenneth Arrow
The first welfare theorem holds that any pure free market economy in equilibrium is necessarily “Pareto efficient”—that it leads to a distribution of resources in which it is impossible to make someone better off without making someone else worse off. Individuals begin with an “endowment” of goods. They trade with each other and reach an equilibrium, which the theorem holds will be efficient.
Pareto efficiency is a weak ethical criterion. A situation in which one rich person has all of a desired good and eveyone else has none of it would be Pareto efficient because it would be impossible to remove some of the good from the rich person without making him worse off. So this first welfare theorem says that markets are efficient but says nothing about the critical issue of distribution.
The second welfare theorem deals with this problem. In an economy there are typically many Pareto-efficient allocations of resources. Some will be fairly equal distributions, some highly unequal. The theorem says that any of these Pareto-efficient distributions can be achieved using free markets—a concept represented by economists as a “contract curve.” However, to achieve a particular one of these allocations, an initial redistribution of individual endowments needs to be made. Then trading can begin, and the particular Pareto-efficient allocation of resources occurs.
The practical implication here is that a government can redistribute resources—through the levying of taxes—and can then depend upon the free market to ensure the eventual allocation is efficient. Equity (fairness) and efficiency go hand in hand.

An Edgeworth box is a way of showing the distribution of goods in an economy. In this example the economy contains two people—Ben and Sarah—and two goods—20 apples and 10 pears. Each point in the box represents a possible distribution of apples and pears between Ben and Sarah. The yellow line is the contract curve, which represents the possible allocation of goods that could be reached by Ben and Sarah after trading with each other. Trading to points on this curve leads to Pareto efficiency.
Arrow and Debreu’s results depend on stringent assumptions: when these don’t hold, efficiency may be compromised, a situation that economists call “market failure.” For the theorems to hold, individuals have to behave according to economic rationality. They need to respond perfectly to market signals, something that is clearly not the case in reality. The behavior of firms has to be competitive, while in practice the world is full of monopolies.
In addition, welfare theorems don’t hold when there are economies of scale, such as in situations in which there are large firms with high set-up costs—for example, in the case of many public utilities companies. A further important condition for the efficiency of equilibrium is that there should be no “externalities.” These are costs and benefits that do not register in market prices. For example the noise from a motorcycle workshop might hurt the productivity of a firm of accountants next door, but the workshop owners do not take this broader cost into account because it doesn’t affect their private costs. Externalities hamper efficiency. Also, if individuals don’t have full information about prices and about the characteristics of the goods they are buying, then markets are likely to fail.
It is tempting to ask what is the point of this model if its assumptions are so removed from reality as to be inapplicable to any situation, but theoretical models aren’t intended to be faithful descriptions of reality: if they were, Arrow and Debreu’s model would be useless. Instead, their theorems answer a central question: under what conditions do markets bring efficiency? The stringency of these conditions, then, tells us by how much and in what ways real economies stray from the benchmark of full efficiency. Arrow and Debreu’s conditions point to what we might do to move closer to efficiency. For instance, we might try to price pollution to deal with externalities, to break up monopolies to make markets more competitive, or to create institutions to help inform consumers about the goods that they buy.
The work of Arrow and Debreu formed the foundation of much of our post-war economics. Attempts were made to refine their findings and to investigate the efficiency of economies under different assumptions. Large macroeconomic models, both theoretical and empirical, were built using Arrow and Debreu’s general equilibrium approach. Some have criticized the equilibrium approach for failing to take into account the chaotic, truly unpredictable nature of real-world economies. These voices have become louder recently with the failure of these kinds of models to predict the 2008 financial crash.

Equilibrium models failed to predict the crisis of 2008, which began when Lehman Brothers Bank collapsed and fired all its staff. This led to criticisms of the models’ basic assumptions.

Born in Calais, France, in 1921, Gérard Debreu was educated at the École Normale Supérieure in Paris during the German occupation. After a period of service in the French army, Debreu returned to his studies of mathematics and developed an interest in economic problems. In 1949, a fellowship allowed him to visit some of the top universities in the US, Sweden, and Norway, bringing him up to date with economic developments that were then unknown in France. In the US he became part of the highly influential Cowles Commission, which had been convened in the 1930s to pursue the mathematical treatment of economic issues. He worked at the US universities of Stanford and Berkeley, teaching economics and mathematics. In 1983, he was awarded the Nobel Prize. He died in 2004.
1954 Existence of an equilibrium for a competitive economy (with K. Arrow)
1959 Theory of Value: An Axiomatic Analysis of Economic Equilibrium