

Decision making
John Nash (1928–)
1928 US mathematician John von Neumann formulates the “minimax rule” that says the best strategy is to minimize the maximum loss on any turn.
1960 US economist Thomas Schelling publishes The Strategy of Conflict, which develops strategies in the context of the Cold War.
1965 German economist Reinhard Selten analyzes games with many rounds.
1967 US economist John Harsanyi shows how games can be analyzed even if there is uncertainty about what sort of opponent you are playing against.
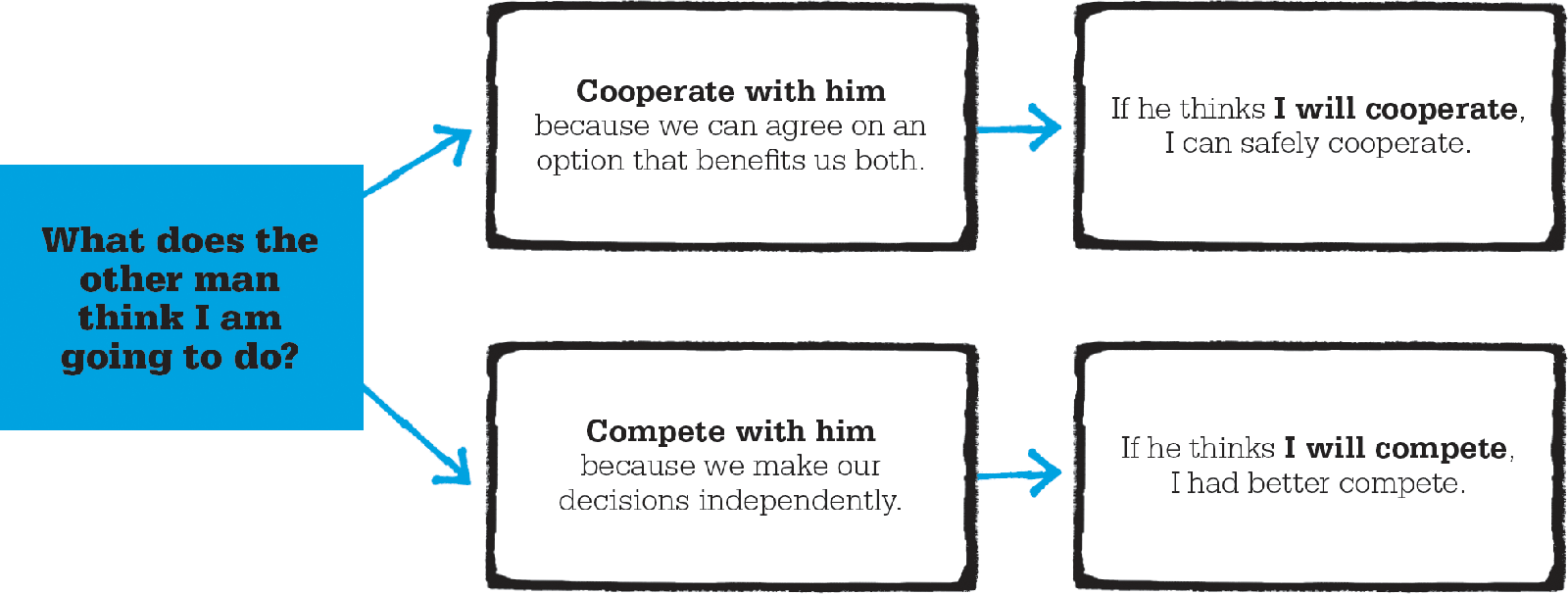
Considering how another person might react when you do something involves making strategic calculations. Successfully negotiating your way through social and economic interactions is a bit like a game of chess, where players must choose a move on the basis of what the other player’s countermove might be. Up to the 1940s economics had largely avoided this issue. Economists assumed that every buyer and seller in the market was very small compared to the total size of the market so nobody had any choice about the price they paid for a good or the wage they sold their labor for. Individual choices had no effects on others, it was reasoned, so they could safely be ignored. But as early as 1838, French economist Antoine Augustin Cournot had looked at how much two firms would produce on the basis of what they thought the other firm was going to do, but this was an isolated case of analyzing strategic interactions.
In 1944, US mathematicians John von Neumann and Oskar Morgenstern published the groundbreaking work, Theory of Games and Economic Behavior. They suggested that many parts of the economic system were dominated by a small number of participants, such as large firms, trade unions, or the government. In such a situation economic behavior needed to be explained with reference to strategic interactions. By analyzing simple two-person games that are “zero-sum” (one person wins and the other loses), they hoped to create general rules about strategic behavior between people in every situation. This became known as game theory.
Von Neumann and Morgenstern looked at cooperative games in which players were given a number of possible actions, each with its own particular result, or payoff. The players were given the opportunity to discuss the situation and come to an agreed plan of action. A real example of such a game was provided by US mathematician Merrill Flood, who allowed his three teenagers to bid for the right for one of them to work as a babysitter for a maximum payment of $4. They were allowed to discuss the problem and form a coalition, but if they were unable to agree between themselves then the lowest bidder would win. To Flood, there were easy solutions to the problem, such as settling by lot or splitting the proceeds equally. However, his children were unable to find a solution and eventually one of them bid 90 cents to do the work.

Our everyday interactions involve strategic decisions that are similar to a game of chess, where players choose their moves on the basis of how they think their opponent will respond.
In the early 1950s a brilliant young US mathematician named John Nash extended this work to look at what happens when players make independent decisions in non-cooperative situations—where there is no opportunity for communication or collaboration. Cooperation is a possible outcome but only if each player sees cooperation as maximizing their own individual chances of success. Nash identified the state of equilibrium in such games where neither player wants to change their behavior. Players are choosing their best strategy on the basis that their opponents are also selecting their best strategies. Nash identified the state in such games where neither player wants to change their behavior as “each player’s strategy is optimal against those of the others.” This is now known as the Nash equilibrium.
"Each player’s strategy is optimal against those of the others."
John Nash
There was an incredible blooming of game theory after World War II, much of it at the think tank RAND (the name comes from Research ANd Development). Set up by the US government in 1946, RAND was charged with putting science at the service of national security. They employed mathematicians, economists, and other scientists to research areas such as game theory, which was seen to be particularly relevant to the politics of the Cold War.
In 1950, the game theorists at RAND devised two examples of non-cooperative games. The first was published under the name “So Long Sucker.” This game was specifically designed to be as psychologically cruel as possible. It forced players into coalitions, but ultimately to win you had to double-cross your partner. It is said that after trials of the game, husbands and wives often went home in separate taxis.
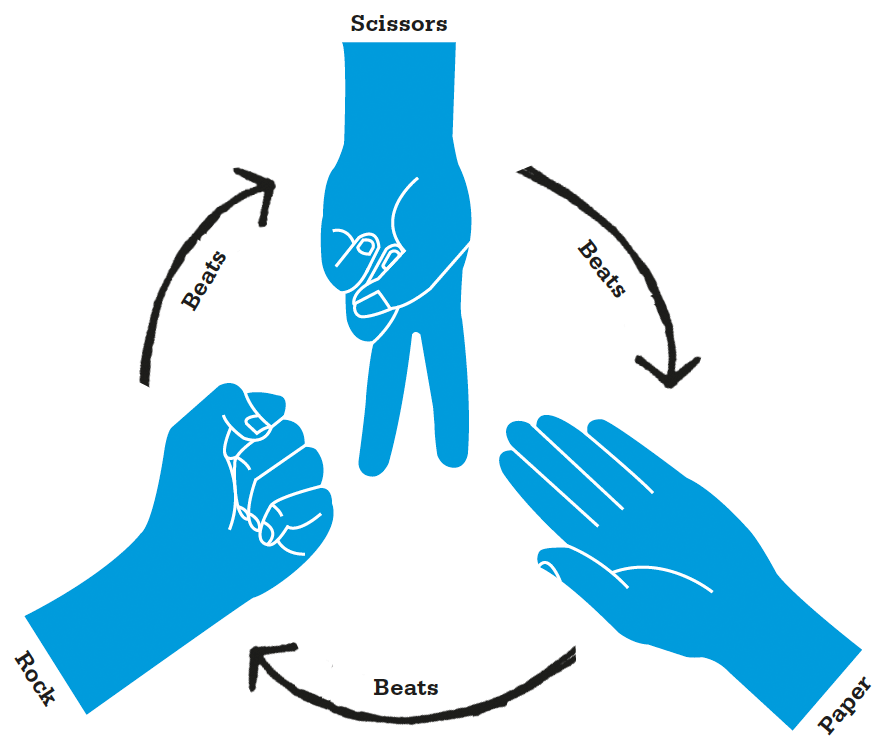
Rock-paper-scissors is an example of a simple zero-sum game in which if one player wins, then the other loses. The game is played by two players. Each player must make one of three shapes with their hand at the same time. The shape one player makes will either match, beat, or lose to their opponent’s shape: rock beats scissors, scissors beats paper, and paper beats rock. Game theorists analyze games such as this to discover general rules of human behavior.
Perhaps the most famous example of a non-cooperative game is the prisoner’s dilemma. It was created in 1950 by Melvin Dresher and Merrill Flood and builds on Nash’s work. The dilemma involves two captured criminals who are kept separate during interrogation and offered the following choices: They are told that if they both testify against each other, they will each get a medium jail sentence that will be painful but bearable. If neither will testify against the other, then they will both receive a short sentence that they will cope with easily. However, if one agrees to testify and the other does not, then the man who testifies will go free, and the man who stayed silent will receive a long sentence that will ruin his life.
The dilemma for each prisoner is this: to betray or not to betray. If he betrays his partner, he will go free or end up with a medium sentence. If he trusts his partner not to betray him, he could end up with a short sentence or a very long time in prison. To avoid the possibility of the “sucker’s payoff”—ending up with a long sentence—the Nash equilibrium is always to betray. What is interesting is that the “dominant” (best) strategy of mutual betrayal does not maximize welfare for the group. If they had both refused to betray, their total jail time would have been minimized.
Dresher and Flood tested the prisoner’s dilemma on two of their colleagues to see whether Nash’s prediction would be true. They made a game where each player could choose to trust or betray the other player. The payoffs were designed so that there was a sucker’s payoff, but also an option for a cooperative trade that would benefit both players, a solution that reflected von Neumann and Morgenstern’s earlier work involving cooperative games. The experiment was run over 100 rounds. This iterative version of the game gave players the chance to punish or reward the previous behavior of their partner. The results showed that the Nash equilibrium of betrayal was only chosen 14 times against 68 times for the cooperative solution. Dresher and Flood concluded that real people learn quickly to choose a strategy that maximizes their benefit. Nash argued that the experiment was flawed because it allowed for too much interaction, and that the only true equilibrium point was betrayal.
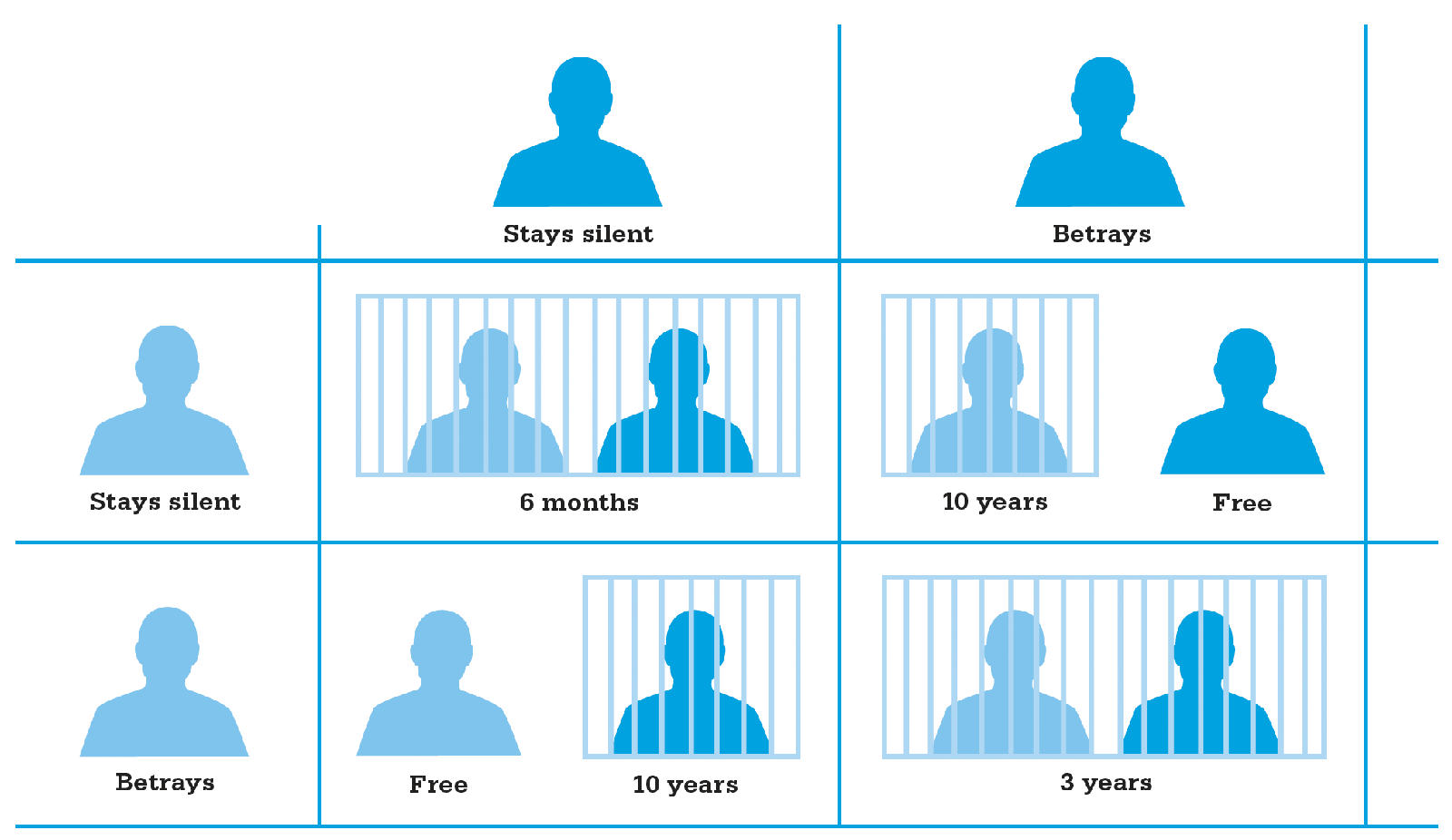
The prisoner’s dilemma is an example of a non-cooperative game in which neither party can communicate with the other. The “Nash equilibrium” of the game is for both players to betray.
The iterative version of the prisoner’s dilemma came to be known as the peace–war game. It was used to explain the best strategy in the Cold War with the Soviet Union. As new technologies such as intercontinental ballistic weapons were developed, each side had to decide whether to invest enormous sums of money to acquire these weapons. The new technology might lead to the ability to win a war relatively painlessly if the other side didn’t develop the new weapon. The consequence of not developing it was either a huge savings of money if the other side didn’t develop it either, or the sucker’s payoff of a total defeat if they did.
The importance of Nash’s work in a wider context was to show that there could be an equilibrium between independent self-interested individuals that would create stability and order. In fact it was argued that the equilibrium achieved by individuals trying to maximize their own payoffs produced safer and more stable outcomes in non-cooperative situations than when the players tried to accommodate each other.
"Game theory is rational behavior in social situations."
John Harsanyi
US economist (1920–2000)
Nash shared the 1994 Nobel Prize for economics with two other economists who helped to develop game theory. Hungarian-born economist John Harsanyi showed that games in which the players did not have complete information about the motives or payoffs of the other players could still be analyzed. Since most real life strategic decisions are made in the fog of uncertainty, this was an important breakthrough. A real life example might be when financial markets cannot be sure of the central bank’s attitude toward inflation and unemployment, and therefore cannot know whether it will increase interest rates to reduce inflation or reduce rates to increase employment. Since the profits of firms in the financial markets are determined by the rate of interest that the central bank will set in the future, firms need to be able to assess the risk of lending more or less money. Harsanyi showed that even if the markets cannot tell which target the central bank is more concerned with, game theory can identify the Nash equilibrium, which is the solution to the problem.

In cooperative games players have the chance to form alliances. In many of these games, such as a tug of war, the only chance an individual has of winning is to cooperate with others.

Expensive technology, such as the Stealth Bomber, was developed during the Cold War. To avoid the “sucker’s payoff,” game theory suggested that both sides should spend this money.

When haggling with a buyer, a seller may start with a price many times what he is happy to accept, but in doing so risks losing the sale.
In 1960, Russian-born economist Leonid Hurwicz began to study the mechanisms by which markets work. In classical theory it is assumed that goods will be traded efficiently: at a fair price and to the people who want them most. In the real world markets do not work like this. For instance Hurwicz recognized that both the buyer and seller of a secondhand car have an incentive to lie about how much each values it.
Even if both parties revealed how much they were willing to buy or sell for and agreed to split the difference in the price, it is unlikely that this mechanism would create an optimal outcome. Sellers will naturally claim to want a much higher price than they actually require, while buyers will offer much less than they are willing to pay. In such circumstances they will fail to come to an agreement even though they both want to make a deal. Hurwicz concluded that if the participants could be persuaded to reveal the truth, then the benefits to both parties would be maximized.
Another economist responsible for advancing game theory was the German Reinhard Selten, who introduced the concept of sub-game perfection in games that are multi-staged. The idea is that there should be an equilibrium at each stage or “sub-game” of the overall game. This can have major implications. An example of such a game is the centipede game, where a number of players pass a sum of money between them, and each time they do so the pile of money is increased by 20 percent. There are two ways for the game to end: the money is passed between them for 100 rounds (hence the name centipede), and then the total pot of money is shared, or at some stage one player decides to keep the pile of money that he or she has been given. Each player’s choice is to cooperate by passing the money on or defect and keep the money. In the last round the player does best by defecting and taking it all. This implies that in the second-to-last round defection is also a better choice—anticipating the future defection of your rival. By continuing this logic backward, it seems that defection dominates in every round so that the sub-game perfect choice is to defect on the first round. This result appears paradoxical, however, given that the sum of money in the first round is very small and hardly worth defecting over.
"You know what you are thinking, but you do not know why you are thinking it."
Reinhard Selten
This idea has been applied to the situation where there is a large chain store with outlets all over the country, and a rival is preparing to enter the market in one or more locations. The chain store could threaten to cut prices in the location that the new firm is thinking of entering. This threat would appear to be both credible and worthwhile since it would not cost the chain store too much profit and would deter the firm from trying to enter in that area. The optimal strategy in terms of Nash equilibrium appears to be for the chain store to fight a price war, and for the new firm not to try to enter the market. However, according to Selten, if the existing firm were forced to cut prices every time a new firm tried to enter one of its markets, the cumulative losses would be too great. Thus, by looking forward and reasoning backward, the threat of a price war is irrational. Selten concludes that the new firm’s entry without a price war is sub-game perfect.
These paradoxes come from the assumption that individuals playing games are fully rational. Selten proposed a more realistic theory of decision making. Although people do sometimes make decisions through rational calculation, often they do so on the basis of past experience and rules of thumb. People may not always use rational calculation. Instead, they may be what game theorists call “boundedly rational:” able to choose the more intuitively appealing solutions to games that may not be sub-game perfect.
Game theory is not without its critics, who say that it tells great stories but fails the main test of any scientific theory: it can make no useful predictions about what will happen. A game might have many equilibriums. An industry resulting in a cartel might be as rational a result as one that descends into a price war. Further, people don’t make decisions based on “If I do this and they do this and I do that and they do that” ad infinitum.
The US economist Thomas Schelling has addressed this issue by studying the idea that the triggers for behavior are not simply based on mathematical probabilities. In the “coordination game,” where both players are rewarded if they think of the same playing card, what card in the pack would you select if you wanted to try to match with someone else? Would you pick the ace of spades?
"When I used to theorize about a nuclear standoff, I didn’t really have to understand what was happening inside the Soviet Union."
Thomas Schelling

Born in 1928 into a middle-class American family, John Nash was labeled as backward at school due to his poor social skills. However, his parents recognized his outstanding academic ability. In 1948, he won a scholarship to Princeton University. His former tutor wrote a one-line letter of recommendation: “This man is a genius.”
At Princeton Nash avoided lectures, preferring to develop ideas from scratch. It was there that he developed the ideas on game theory that were to earn him his Nobel Prize. In the 1950s he worked at the RAND Corporation and MIT (Massachusetts Institute of Technology), but by now his mental state was worsening. In 1961, his wife committed him for treatment for his schizophrenia. Nash battled with the condition for the next 25 years but never stopped hoping that he would be able to add something else of value to the study of mathematics.
1950 Equilibrium Points in N-person Games
1950 The Bargaining Problem
1952 Real Algebraic Manifolds