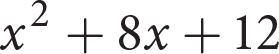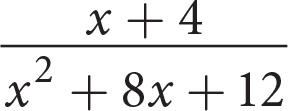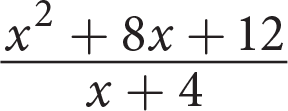Chapter 3

The Method for SAT Math Questions

How to Do SAT Math

SAT Math questions can seem more difficult than they actually are, especially when you are working under time pressure. The method we are about to describe will help you answer SAT questions, whether you are comfortable with the math content or not. This method is designed to give you the confidence you need to get the right answers on the SAT by helping you think through a question logically, one piece at a time.

Take a look at this question and take a minute to think about how you would attack it if you saw it on test day:

Building M is an apartment building in city Z. According to data kept by the housing commission in city Z, 24% of the 150 apartments in building M have at least 3 bedrooms. There are 1,350 apartment buildings in city Z and the average number of apartments in those buildings is 150. If building M is representative of the apartment buildings in city Z, then which of the following is the best estimate of how many apartments in city Z have fewer than 3 bedrooms?
1. 48,600
2. 67,500
3. 153,900
4. 202,500

Many test takers will see a question like this and panic. Others will waste a great deal of time reading and re reading without a clear goal. You want to avoid both of those outcomes.

Start by defining clearly for yourself what the question is actually asking. What do the answer choices represent? In this question, they represent the number of apartments in city Z that have fewer than 3 bedrooms. Page 24

Next, examine the information that you have and organize it logically. The question asks about the number of apartments with fewer than 3 bedrooms. Okay, then what information do you have about number of bedrooms? You know that 24% of the 150 building M apartments have at least 3 bedrooms. That’s the opposite of fewer than 3. You can deduce that 100% − 24% = 76% of the 150 apartments in building M have fewer than 3 bedrooms.

Now make a strategic decision about how to proceed. The answer choices are far apart, so you might consider rounding 76% to $\text{[math]}$ and estimating. However, this question appears on the calculator section, and it’s a quick calculation. Let’s say that you decide to use your calculator. Plug the numbers into your calculator and jot down what you know so far:

Fewer than 3 in building M: 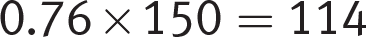$\text{[math]}$

The question asks for the number of apartments in city Z with fewer than 3 bedrooms, so hunt for information tying building M to city Z. You’re told that the average number of apartments in city Z buildings is 150, which is identical to the number of apartments in building M, and that building M is “representative” of the apartment buildings in city Z. Translation: what is true for building M is also true for all apartment buildings in city Z. You also know that there are 1,350 apartment buildings in city Z. You can deduce that the number of apartments with fewer than 3 bedrooms in building M (114) times the total number of apartment buildings in city Z (1,350) will give you the number of apartments with fewer than 3 bedrooms in all of city Z. Plug that into your calculator:

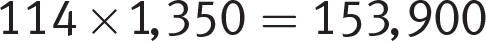
Finally, confirm that you answered the right question: you want the number of apartments in city Z with fewer than 3 bedrooms. Great! You’re done; the correct answer is (C).

Here are the steps of the method we just used:

Method for SAT Math Questions
Step 1.	State what the question is asking
Step 2.	Examine the given information
Step 3.	Choose your approach
Step 4.	Confirm that you answered the right question

You can think of these steps as a series of questions to ask yourself: What do they want? What are they giving me to work with? How should I approach this? Did I answer the right question?

Not all SAT Math questions will require time spent on all the steps. The question above, because it is a word problem, required a fair amount of analysis in steps 1 and 2, but choosing an approach (step 3) was straightforward; the calculations were quick to do on a calculator, so there was no need to estimate. Other questions will require very little thought in steps 1 and 2 but will benefit from a careful strategy decision in step 3. Step 4 is always quick, but you should always do it: just make sure you answered the question that was actually asked before you bubble in your response. Doing so will save you from speed mistakes on questions that you know how to do and should be getting credit for.

There are several approaches you can choose from in step 3: doing the traditional math, as we did in the question above; Picking Numbers; Backsolving; estimating; or taking a strategic guess. In the next two examples, you’ll see Picking Numbers and Backsolving in action.Page 25

Here’s another example. This one is not a word problem, so steps 1 and 2 require negligible mental energy, but pay attention when you get to step 3.

Which of the following is equivalent to the expression $\text{[math]}$ ?
1. $\text{[math]}$
2. $\text{[math]}$
3. $\text{[math]}$
4. $\text{[math]}$

Step 1: What do they want? An answer choice that is equal to $\text{[math]}$ .

Step 2: What do they give you? Only the expression 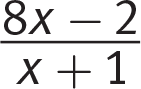$\text{[math]}$ .

Step 3: What approach will you use?

Here’s where it gets interesting. The creator of this question may be expecting you to use polynomial long division to solve, and we’ll cover that technique in chapter 11 because you may want to have it in your arsenal. But if you don’t know how to do polynomial long division, there’s no need to panic. You could use an alternate approach called Picking Numbers that will work just as well: choose a number to substitute for x in the question, then substitute the same number for x in the choices and see which one matches. Like this:

Pick a small number for x, say 2. When x = 2, the original expression becomes:

$\text{[math]}$

Now plug x = 2 into the choices:

(A): 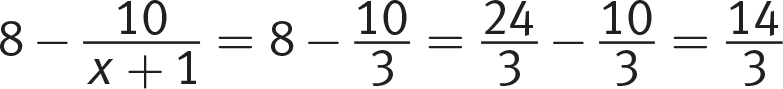$\text{[math]}$

This is a match. It is always possible that another answer choice can produce the same result, so check the rest to be sure there isn’t another match when x = 2. (If there is, go back and pick another number to distinguish between the choices that match.)

(B) 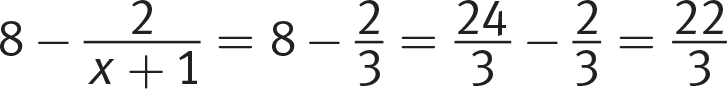$\text{[math]}$

Eliminate (B).

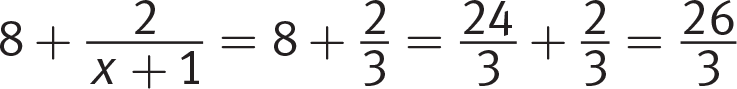
Eliminate (C).

(D) $\text{[math]}$

Eliminate (D).

Step 4: Did you solve for the right thing? You found the equivalent expression, so yes. Only (A) is a match, so it is the correct answer.Page 26

When picking numbers, use numbers that are permissible and manageable. That is, use numbers that are allowed by the stipulations of the question and that are easy to work with. In this question, you could have picked any real number because x was not defined as positive, negative, odd, even, a fraction, etc. A small positive integer is usually the best choice in this situation. In other questions, other kinds of numbers may be more manageable. For example, in percents questions, 100 is typically a smart number to pick.

Try one more:

Mr. Dvorkin is distributing colored markers to a group of children. If he gives each child 4 markers, he will have 3 markers left over. In order to give each child 5 markers, with no markers left over, he will need 17 additional markers. How many markers does Mr. Dvorkin have?
1. 55
2. 68
3. 83
4. 101

Step 1: What do they want? The number of markers.

Step 2: What do they give you? Two unknowns (the number of children and the number of markers) and sufficient information to set up a system of equations.

Step 3: What approach will you use? You could set up the system of equations, but it might be faster to use a technique called Backsolving: plug the choices in for the unknown and see which one works. Here, you need an answer choice that will leave a remainder of 3 when divided by 4. Choices (B) and (D) don’t meet this condition, so the answer must be (A) or (C).

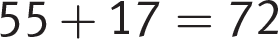(A) If Mr. Dvorkin has 55 markers, and gives each child 4 markers, he will indeed have 3 markers left over, since $\text{[math]}$ . Now, what happens in the other situation? With an extra 17 markers, Mr. Dvorkin should be able to give each child exactly 5 markers. But $\text{[math]}$ , which is not evenly divisible by 5. Eliminate (A).

You’ve now eliminated every choice but (C), so it must be correct—you don’t even need to test it! For the record:

(C) If Mr. Dvorkin has 83 markers and gives each child 4 markers, he will indeed have 3 left over, since 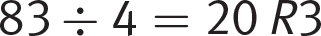$\text{[math]}$ . With an extra 17 markers, Mr. Dvorkin should be able to give each child exactly 5 markers, and this is in fact what happens: $\text{[math]}$ , which is evenly divisible by 5.

Step 4: Did you solve for the right thing? The question asked for the number of markers. You found that 83 markers satisfies all conditions of the problem. Choose (C) and move on.

Although it wasn’t the case in this question, when backsolving it often makes sense to start with (B) or (C) in case you can tell from the context whether you’ll need a larger or smaller answer choice if the one you’re testing fails.

Now, it’s your turn. Be deliberate with these questions. If there is analysis to do up front, do it. If there is more than one way to do a question, consider carefully before choosing your approach. And be sure to check whether you answered the right question. Forming good habits now, in slow and careful practice, will build your confidence for test day. Page 27

Try on Your Own

Directions: Take as much time as you need on these questions. Work carefully and methodically. There will be opportunities for timed practice in future chapters.

A cargo airplane has a maximum takeoff weight of 19,000 kilograms. The airplane, crew, and fuel have a combined weight of 14,750 kilograms. The airplane will be loaded with n identical cargo containers, each of which has a weight of 125 kilograms. What is the greatest value of n such that the airplane does not exceed its maximum takeoff weight?
1. 28
2. 34
3. 118
4. 152
A certain model of laptop computer is priced at $550 at a local electronics store. The same model laptop at an online retailer sells for $\text{[math]}$ of the electronics store’s price. At a luxury department store, the same model laptop sells for $\text{[math]}$ of the electronics store’s price. How many dollars more is the cost of the laptop at the luxury department store than at the online retailer?
1. 198
2. 220
3. 275
4. 495
A stack of 75 identical plastic plates forms a column approximately 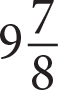$\text{[math]}$ inches tall. At this rate, which of the following is closest to the number of plates that would be needed to form a column 20 inches tall?
1. 125
2. 150
3. 185
4. 220
Last month, Kiera ran 22 more miles than Bianca did. If they ran a combined total of 86 miles, how many miles did Bianca run?
1. 27
2. 32
3. 43
4. 54
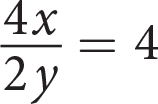If $\text{[math]}$ , what is the value of $\text{[math]}$ ?
1. $\text{[math]}$
2. $\text{[math]}$
3. $\text{[math]}$
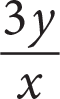4. 2
x 2 4 6 8 10

y $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Which of the following equations relates y to x according to the values shown in the table above?
1. $\text{[math]}$
2. $\text{[math]}$
3. $\text{[math]}$
4. $\text{[math]}$
Page 28
$\text{[math]}$

In the equation above, c is a constant. If n = 5, what is the value of c?
1. –1
2. 0
3. 3
4. 11
At a child’s lemonade stand, p pitchers of lemonade are made by adding m packets of lemonade mix to cold water. If m = 2p + 4, how many more packets of lemonade mix are needed to make each additional pitcher of lemonade?
1. 0
2. 1
3. 2
4. 4
A health club charges a one-time membership fee of $125 plus n dollars for each month. If a member pays $515 dollars for the first six months, including the membership fee, what is the value of n?
1. 55
2. 65
3. 75
4. 85
If x > 0, which of the following is equivalent to $\text{[math]}$ ?
1. $\text{[math]}$
2. $\text{[math]}$
3. $\text{[math]}$
4. $\text{[math]}$

x	2	4	6	8	10
y	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

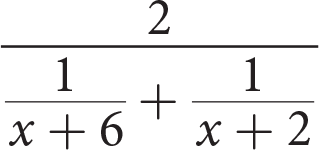Page 29

A Note About Grid-ins

You will see an occasional question without answer choices throughout the Math chapters of this book, starting in the next chapter. On the SAT, several of these Grid-in questions appear at the end of each Math section. Instead of bubbling in a letter, you’ll enter your responses to these questions into a grid that looks like this:

If you are gridding a value that doesn’t take up the whole grid, such as 50, you can enter it anywhere in the grid as long as the digits are consecutive; it doesn’t matter which column you start in. Gridding mixed numbers and decimals requires some care. Anything to the left of the fraction bar will be read as the numerator of a fraction, so you must grid mixed numbers as improper fractions. For instance, say you want to grid the mixed fraction 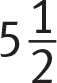$\text{[math]}$ . If you enter 5 1 / 2 into the grid, your answer will be read as 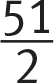$\text{[math]}$ . Instead, enter your response as 1 1 / 2, which will be read (correctly) as $\text{[math]}$ . Alternatively, you could grid this answer as 5.5.

A repeating decimal can either be rounded or truncated, but it must be entered to as many decimal places as possible. This means it must fill the entire grid. For example, you can grid $\text{[math]}$ as .166 or .167 but not as .16 or .17.

Note that you cannot grid a minus sign or any value larger than 9,999, so if you get an answer that is negative or larger than 9,999 to a grid-in question, you’ve made a mistake and should check your work.

Page 30

Reflect

Directions: Take a few minutes to recall what you’ve learned and what you’ve been practicing in this chapter. Consider the following questions, jot down your best answer for each one, and then compare your reflections to the expert responses on the following page. Use your level of confidence to to determine what to do next.Page 31

Think about your current habits when attacking SAT questions. Are you a strategic test taker? Do you take the time to think through what would be the fastest way to the answer?

Do word problems give you trouble?

What are the steps of the Method for SAT Math, and why is each step important?

Expert Responses

Think about your current habits when attacking SAT questions. Are you a strategic test taker? Do you take the time to think through what would be the fastest way to the answer?

If yes, good for you! If not, we recommend doing questions more than one way whenever possible as part of your SAT prep. If you can discover now, while you’re still practicing, that Picking Numbers is faster for you on certain types of questions but not on others, you’ll be that much more efficient on test day.

Do word problems give you trouble?

If word problems are difficult for you, get into the habit of taking an inventory, before you do any math, of what the question is asking for and what information you have.

What are the steps of the Method for SAT Math, and why is each step important?

Here are the steps:

Step 1. State what the question is asking
Step 2. Examine the given information
(Taking an inventory is especially important in word problems.)
Step 3. Choose your approach
(Taking a moment to decide what approach will be the fastest way to the answer will ultimately save you time.)
Step 4. Confirm that you answered the right question
(Making sure you solved for the right thing will save you from losing points to speed mistakes on questions that you know how to do and should be getting credit for.)

Next Steps

If you answered most questions correctly in the “How Much Have You Learned?” section, and if your responses to the Reflect questions were similar to those of the SAT expert, then consider the Method for SAT Math Questions an area of strength and move on to the next chapter. Do keep using the method as you work on the questions in future chapters.

If you don’t yet feel confident, review those parts of this chapter that you have not yet mastered and try the questions you missed again. As always, be sure to review the explanations closely.Page 32

Answers and Explanations

B

Difficulty: Medium

Category: Solving Equations

Strategic Advice: Break apart the question into its mathematical parts; determine what information you have and what value you need to find and then determine how you’ll find that value.

Getting to the Answer: You’re given the weight of everything on the airplane except the combined weight of the cargo containers and you’re given the maximum takeoff weight of the plane. Therefore, the difference between the maximum takeoff weight and the weight of the plane, crew, and fuel must be the maximum combined weight of the cargo containers.

You’re also told that n represents the number of cargo containers that will be loaded on the plane and that each container weighs 125 kilograms. You need to find the number of containers, n, that make up the difference in weights.

The maximum takeoff weight of the plane is 19,000 kilograms and the weight of the plane, crew, and fuel is 14,750 kilograms. Hence, the maximum number of cargo containers can have a combined weight no greater than 19,000 − 14,750 = 4,250 kilograms. That means that the maximum number of containers, n, must be 4,250 kilograms ÷ 125 kilograms = 34 containers. Thus, (B) is correct.

The maximum takeoff weight of the plane is 19,000 kilograms, and the weight of the plane, crew, and fuel is 14,750 kilograms. Hence, the maximum number of cargo containers can have a combined weight no greater than 19,000 − 14,750 = 4,250 kilograms. That means that the maximum number of containers, n, must be 4,250 kilograms ÷ 125 kilograms = 34 containers. Thus, (B) is correct.

The maximum takeoff weight of the plane is 19,000 kilograms and the weight of the plane, crew, and fuel is 14,750 kilograms. Hence, the maximum number of cargo containers can have a combined weight no greater than 19,000 - 14,750 = 4,250 kilograms. That means that the maximum number of containers, n, must be 4,250 kilograms ÷ 125 kilograms = 34 containers. Thus, (B) is correct.
C

Difficulty: Medium

Category: Solving Equations

Strategic Advice: Think about what you’re being asked to find—the difference between the price of the laptop at the luxury department store and at the online retailer—and what information you’re given—the actual price at a local electronics store and two fractions of that price that represent the prices at the online retailer and at the luxury department store.

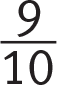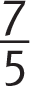Getting to the Answer: The price of the laptop at the electronics store is $550. You also know that the price at the online retailer is $\text{[math]}$ of this, so that price is $\text{[math]}$ . The question also states that the price at the luxury store is $\text{[math]}$ of the price at the electronics store, so that’s 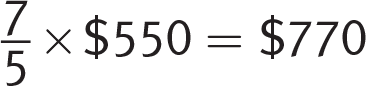$\text{[math]}$ . Therefore, the difference between the price at the luxury department store and the price at the online retailer is $770 – $495 = $275. Choice (C) is correct.
B

Difficulty: Easy

Category: Proportions

Strategic Advice: Because the answer choices are widely spaced apart, and the question asks for the answer that is “closest to the number,” estimation will be a better approach than wading into unnecessarily detailed and tedious calculations.

Getting to the Answer: Notice the relationship between the height of the stack of 75 plates and the height of the unknown number of plates: $\text{[math]}$ inches is about half of 20 inches. Put another way, a 20-inch stack of plates will be about twice as tall as a stack of 75 plates. Therefore, it’s logical to deduce that approximately twice as many plates, or about 2 × 75 = 150, will be needed to form a stack 20 inches tall. Hence, (B) is correct.
B

Difficulty: Medium

Category: Heart of Algebra / Systems of Linear Equations

Strategic Advice: Use the answer choices to your advantage to quickly find Bianca’s distance.

Getting to the Answer: The question gives two unknowns and enough information to create a system of equations; therefore, it could be solved with a traditional algebraic approach.

There is, however, a more efficient way: assess the answer choices to see which makes sense for Bianca’s distance. Since Kiera ran 22 miles farther than Bianca, and the combined distance they ran is 86 miles, Bianca must have run less than half of 86 miles. Since one-half of 86 is 43, you can quickly eliminate (C) and (D), which are both too big.

Now check (B) against the known information. If Bianca ran 32 miles, then Kiera ran 32 + 22 = 54 miles. Check if Bianca’s distance and Kiera’s distance add up to 86: 32 + 54 = 86; thus, (B) is correct.Page 33

If you’re curious about the algebraic approach, here it is: let b stand for the number of miles Bianca ran and k stand for the number of miles Kiera ran. Then b + k = 86, and k = b + 22. Now, substitute the value of k in terms of b into the first equation:

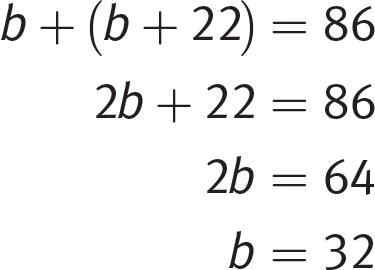
Again, Bianca ran 32 miles, and (B) is correct.
C

Difficulty: Medium

Category: Solving Equations

Strategic Advice: You have two variables, but only one equation, so solving for each variable will not be possible. Instead, pick numbers for x and y that will make the equation true.

Getting to the Answer: Pick a simple number for x, solve for y, and if y is also easy to work with, plug them into the expression you’re trying to find. Say x = 2; then you have 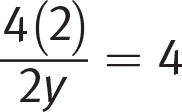$\text{[math]}$ , which simplifies to $\text{[math]}$ . Solving for y, you multiply both sides by 2y and get 8 = 8y, so y = 1, another manageable number.

Now, plug these same values of x and y into $\text{[math]}$ to get $\text{[math]}$ . Thus, (C) is correct.
D

Difficulty: Medium

Category: Heart of Algebra / Linear Equations

Strategic Advice: The answer choices are split into two types: the first two are exponential and the second two are linear. Therefore, to quickly narrow down the answers, examine the table to determine whether the change in x-values versus y-values is exponential or linear.

Getting to the Answer: Notice that, for every increase of 2 in the x-value, the y-value increases by $\text{[math]}$ . Therefore, you have a linear relationship, so you can eliminate (A) and (B), which are both exponential functions.

Now, plug values from the table into the remaining answers to see whether the math works out. Try the first column in the table and plug in 2 for x and $\text{[math]}$ for y:

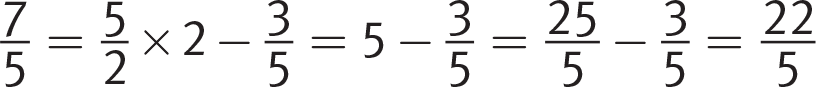(C): $\text{[math]}$ . This doesn’t work out, so (D) must be correct. No need to check it. For the record:

(D): $\text{[math]}$
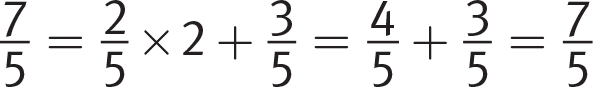
D

Difficulty: Medium

Category: Heart of Algebra / Linear Equations

Strategic Advice: Backsolve by plugging the answer choices in for c to determine which one makes the given equation true.

Getting to the Answer: The question provides a linear equation and the value of one of the variables.

Since you’re told that n = 5, fill this value into the equation, and then simplify to find the root:

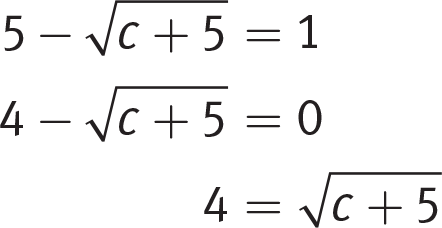
Simplifying to this point makes it easier to see if the value of c you plug in works. Now check the answer choices, starting with (B) or (C). If the answer you choose is too large or too small, you’ll know which direction to go when testing the next choice.

(B):   $\text{[math]}$ . This answer is too small, so try (C) next.

(C):   $\text{[math]}$ . This choice is still too small, so the correct choice must be (D). No need to check it. For the record:

(D):   $\text{[math]}$ .

If you prefer the algebraic approach, here it is:

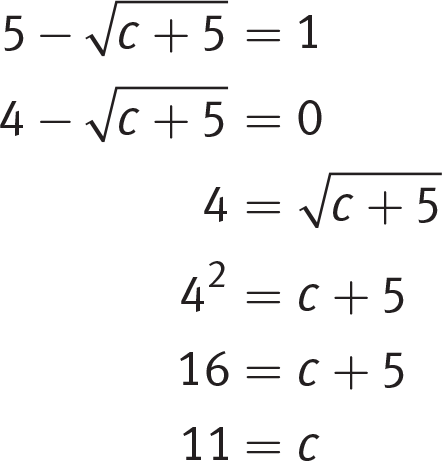
Page 34Again, (D) is correct.
C

Difficulty: Medium

Category: Heart of Algebra / Linear Equations

Strategic Advice: Pick a number for p to determine how many packets of mix will be needed, and then pick another number for p to see how the number of packets changes.

Getting to the Answer: Say p = 2, then m = 2(2) + 4 = 8, so there are 8 packets of mix needed to make 2 pitchers of lemonade. Now try p = 3: m = 2(3) + 4 = 10. For one additional pitcher, the packets needed increased from 8 to 10, which is a change of 2. Therefore, (C) is correct. You can confirm by trying p = 4, then m = 2(4) + 4 = 12.
B

Difficulty: Medium

Category: Heart of Algebra / Linear Equations

Strategic Advice: Backsolve by plugging the answer choices in for n to determine which one matches the given price of six months of membership.

Getting to the Answer: Check the answer choices, starting with (B) or (C). If the answer you choose is too large or too small, you’ll know which direction to go when testing the next choice. Multiply the value in the answer choice by the six months and then add the $125 membership fee.

(B): $65 × 6 = $390. $390 + $125 = $515. This is a match, so (B) is correct. Since there can be only one correct answer, you’re finished.

Alternatively, you can solve algebraically:

(B) is correct.
D

Difficulty: Medium

Category: Heart of Algebra / Linear Equations

Strategic Advice: Pick a number for x to determine the numerical value of the given expression, then plug the same number into the answer choices to find the one that matches.

Getting to the Answer: To make calculations easy, say x = 1; then the given expression becomes 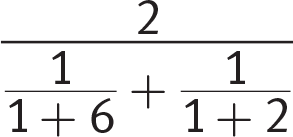$\text{[math]}$ . Now, simplify this expression:

Next, plug 1 in for x in the answer choices to see which yields the same value:

(A): 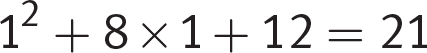  $\text{[math]}$ . Eliminate.

(B):   $\text{[math]}$ . Eliminate.

(C):   $\text{[math]}$ . Eliminate. You have eliminated three answer choices so the one left is correct; (D) is correct.

For the record: (D): $\text{[math]}$ . This is a match, which confirms that (D) is correct.

You might also have noticed that (B) gave you the reciprocal of the value you were looking for; therefore, the reciprocal of the expression in (B) must give you the correct answer, and that is (D).