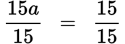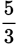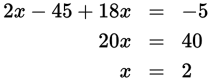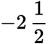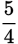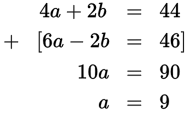Algebra Review

The difference between algebra and arithmetic is that algebra uses symbols called variables, such as x and y, to generalize arithmetic relationships.

Algebra problems on the ASVAB can appear in two forms: as straightforward math problems or as word problems. You will find that algebra problems on the Mathematics Knowledge section are often good candidates for a strategic approach, such as Picking Numbers or Backsolving. Nonetheless, if you are comfortable with algebra, using straightforward math may be faster than using a strategy on some problems. You want to have all these tools—Picking Numbers, Backsolving, Strategic Guessing Using Logic, a combination of approaches, and straightforward math—in your toolkit on Test Day.

Terms and Expressions

A term is a number, a variable, or one or more numbers multiplied by one or more variables. Here are some examples:

4	3x	7ab2

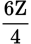
An algebraic expression on the ASVAB test could look like this:

(11 + 3x) − (5 − 2y)

If an expression consists of one term, it is a monomial. If it consists of two terms, it is a binomial. If it consists of more than two terms, like the one above, then it is a polynomial.

You can only add or subtract “like terms.” Like terms have the same variables and the same exponents. The following pairs of terms are like terms:

3a + 7a	10z² − 5z²

To combine like terms, add or subtract the coefficients (the numbers that come before the variables) of terms that have the same variable raised to the same exponent as explained in chapter 6. Do not change the variables. Here are some examples:

6a + 5a = 11a

8b² − 2b² = 6b²

3a + 2b − 8a = 3a − 8a + 2b = −5a + 2b or 2b − 5a

Remember, you cannot combine unlike terms such as these:

6a + 5a²

3a + 2b

Study this example:

Question	Analysis
Simplify: (11 + 3x) − (5 − 2x)
= 11 + 3x − 5 + 2x	Distribute the minus sign across the parentheses.
= 3x + 2x + 11 − 5	Group like terms together.
= 5x + 6	Combine like terms.

Multiplying and dividing monomials is different from adding and subtracting them. In addition and subtraction, you can combine only like terms. With multiplication and division, however, you can multiply and divide terms that are different. When you multiply monomials, multiply the coefficients of each term, add the exponents of like variables, and multiply different variables together. Study this example:

Question	Analysis
Simplify: (6a)(4b)
= (6 × 4)(a × b) = 24ab	Multiply the coefficients by each other and the variables by each other.

Now try one on your own.

Simplify: (6a)(4ab) + (3a²)(8b) = ?

Explanation

Step 1: The question presents an expression.

Step 2: You need to simplify the expression.

Step 3: Multiply the coefficients together, and multiply the variables together. Remember not to add or subtract unless you’re dealing with like terms.

(6a)(4ab) + (3a²)(8^b) =
(6 × 4)(a × a × b) + (3 × 8) (a² × b) =
(6 × 4)(a¹⁺¹ × b) + (3 × 8) (a² × b) =
24a²b + 24a²b =
48a²b

The answer is 48a²b.

Step 4: Review your work to ensure you multiplied correctly.

To multiply binomials, use the FOIL method. FOIL stands for First, Outer, Inner, Last and refers to the position of each term in the parentheses. Here’s an example:

Question	Analysis
Simplify: (y + 1)(y + 2)
First terms: (y × y) Outer terms: (y × 2) Inner terms: (1 × y) Last terms: (1 × 2) = y² + 2y + y+ 2	Use FOIL to multiply each term in the binomials.
= y² + 3y + 2	Combine like terms.

The final expression above, y² + 3y + 2, is known as a quadratic expression. A quadratic expression contains variables raised to the exponent of 2, in other words, variables that are squared. An expression without an exponent is a linear expression.

You may occasionally be called upon to factor a quadratic expression or equation on the ASVAB. Do this with “reverse-FOIL.” Take a look:

Question		Analysis
Factor: x² − 4x − 21
(x )(x )		To begin, build parentheses with the First terms that multiply to x2.
1	−21	What Last terms will multiply to produce −21?
3	−7
7	−3
21	1
3	−7	Which of these pairs will add to produce −4?
(x + 3)(x − 7)		Plug these into the parentheses.

Classic Quadratics

If you learn to recognize the following three common quadratics, you can multiply them and factor them without needing to FOIL or reverse-FOIL:

If you see a perfect square, such as x² or 16, on each end of a quadratic, it is probably one of these classic quadratics.

Study this example.

Question	Analysis
Which of the following is equivalent to the expression a² − b²?	Step 1: The question gives a quadratic expression. Step 2: You are asked to find the answer that is the same expression, expressed in a different form. Step 3: Use math knowledge to recognize that this is a classic quadratic. a² − b² = (a + b)(a − b).
(A) (a − b)² (B) (a + b)² (C) (a + b)(a − b) (D) a² − 2ab + b²	The answer is (C). Step 4: Briefly check your calculations.

Equations with One Variable

An equation is two expressions separated by an equal sign. The key to solving equations is to do the same thing to both sides of the equation until you have your variable isolated on one side of the equal sign and everything else on the other side.

Question

Analysis

Solve for a:
12a + 8 = 23 − 3a

Step 1: The question presents an equation with one variable, a.

Step 2: The task is to find the value of a.

Step 3: (B) is a fraction, which makes backsolving potentially awkward. Use straightforward math to isolate the variable.

12a + 8 = 23 − 3a

12a = 15 − 3a

15a = 15

a = 1

(A)	1
(B)
(C)	2
(D)	11

Step 4: Plug 1 in for a in the equation:

Answer choice (A), a = 1, works and is correct.

Try it on your own.

Solve for x: 2x + 7 = .

Explanation

Step 1: This is a linear equation with one variable.

Step 2: You need to find the value of that variable.

Step 3: Multiply each side by 4 to eliminate the fraction:

4 × (2x + 7) = 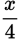× 4

8x + 28 = x

Subtract x from both sides:

7x + 28 = 0

Subtract 28 from both sides:

7x = −28

Divide both sides by 7:

x = −4

Step 4: To confirm, plug −4 into the original equation for x:

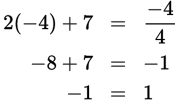
The answer –4 works and is correct.

Equations with Two Variables

Sometimes a problem will give you the numerical value of the variables and ask you for the value of an expression with those variables in it. To solve, just plug the values into the equation. Be sure to follow the rules of PEMDAS (see chapter 6 on arithmetic) and be careful with your calculations.

Question	Analysis
If x = 15 and y = 10, what is the value of 4x(x − y)?
4(15)(15 − 10)	Plug 15 in for x and 10 in for y.
= 4(15)(5) = (60)(5) = 300	Use PEMDAS and solve.

Sometimes you are given an equation with two variables and asked to solve for one variable in terms of the other. This means that you must isolate the variable for which you are solving on one side of the equation and put everything else on the other side. In other words, when you’re done, you’ll have x (or whatever the variable is) on one side of the equation and an expression on the other side.

Question	Analysis
Solve 7x + 2y = 3x + 10y − 16 for x in terms of y.
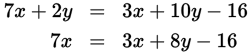
	Subtract 2y from both sides to get all the y’s on one side of the equation.
	Subtract 3x from both sides to get all the x’s on the other side of the equation.
x = 2y − 4	Divide both sides by 4 to isolate x. The solution for x in terms of y is 2y − 4.

Try the next one on your own.

Solve 16t + 16u(3) + 8 = −4t − 2u − 6 for t in terms of u.

Explanation

Step 1: You are given an equation with two variables.

Step 2: You need to solve for the variable t, but you will not end up with one numerical value. The variable t will be equal to an expression that contains u.

Step 3: First, use PEMDAS to simplify the left side of the equation.

16t + 18u + 8 = −4t −2u −6

Then, add 4t to both sides to get all of the t’s on one side of the equation.

20t +18u + 8 = −2u −6

Subtract 18u from both sides.

20t + 8 = −20u −6

Subtract 8 from both sides.

20t = −20u −14

Divide both sides by 20.

t = −u − 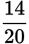= −u −

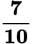
Step 4: Check that you performed all of your calculations correctly.

Systems of Equations

On the ASVAB, you may be presented with two equations with two variables and be asked to solve for the value of one of the variables. There are two ways to do this: substitution and combination.

Substitution

Using the substitution technique, you will use one equation to express one variable in terms of the other. Then you’ll substitute that expression for that variable into the other equation.

Question

Analysis

Find the value of x:

6x + y = 15

2x − 3y = −5

Step 1: The question gives you two linear equations with two variables.

Step 2: You need to solve for one variable, x.

Step 3: It is easy to isolate y in the first equation, so use substitution to do so: y = −6x + 15.

Plug in −6x + 15 for y in the second equation:

Solve for x:

(A)
(B)
(C)	2
(D)	3

Choice (C) is correct.

Step 4: Briefly confirm that you followed PEMDAS and performed the calculations correctly.

Alternatively, you could use Backsolving on that problem. Here’s how that might work: answer choice (C) is probably the easiest one to start with, since it’s a whole number. Plug 2 in for x in 6x + y = 15 and solve for y:

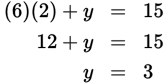
Then check x = 2 and y = 3 in the other equation:

The answer, x = 2, works in both equations and is correct.

Combination

The other way to solve for the value of a variable when you have two variables and two equations is to combine the two equations by adding or subtracting them in such a way that you eliminate one of the variables. Then you can solve for the remaining variable.

Question

Analysis

Find the value of a:

4a + 2b = 44

6a − 2b = 46

Step 1: The question gives you two linear equations with two variables.

Step 2: You need to solve for one variable, a.

Step 3: If you add the two equations together, you will eliminate b. This can be done by using combination.

(A)	4
(B)	9
(C)	10
(D)	12

Choice (B) is correct.

Step 4: Briefly confirm that you performed the calculations correctly.

Alternatively, you could use Backsolving on that problem. Here’s how that might work: if you decided to start with choice (B), you would plug 9 in for a in 4a + 2b = 44 and solve for b:

Then check a = 9 and b = 4 in the other equation:

The answer, a = 9, works in both equations and is correct.

Try it on your own.

Solve for x:

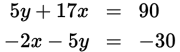
Explanation

Step 1: You are given two linear equations with two variables.

Step 2: You need to find the value of one of the variables, x.

Step 3: The term 5y appears in both equations, so combination will allow you to get rid of the y term efficiently. Rearrange the terms of the first equation to make them easier to add together.

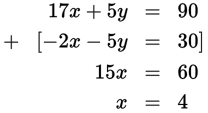
The correct answer is x = 4.

Step 4: To confirm your answer, check that you performed all of the calculations correctly.

Quadratic Equations with Variables

When an equation has a quadratic expression on one side and zero on the other side, you can use factoring to solve for the value or values of the variable.

Question	Analysis
Solve for y: y² + 4y + 3 = 0
(y + 3)(y + 1) = 0	Factor the left side of the equation.
If y + 3 = 0, then y = −3. If y + 1 = 0, then y = −1. Therefore, y = −3 or −1.	Whenever multiplication results in zero, at least one of the factors must equal zero. Use this fact to solve for y.

Note that the solution to a quadratic equation often has two values. The only time you will get a single value for the variable is when the factors are the same, as in this example that uses one of the classic quadratics you learned about above:

Question	Analysis
Solve for x: x² − 6x + 9 = 0.
(x − 3)(x − 3) = 0	Either factor the left side of the equation using reverse-FOIL or use your knowledge of classic quadratics to factor.
If x − 3 = 0, then x = 3.	Whenever multiplication results in zero, at least one of the factors must equal zero. Since both of the factors are the same, you will only get one result for x.

If you see a quadratic expression set equal to a quantity other than zero, simply manipulate the equation so that the expression is set equal to zero. Similarly, if you see a quadratic expression presented in a different order, simply move the terms around in order to put it in the form ax² + bx + c = 0. Study this example:

Question	Analysis
Solve for x: −4 + 2x = 31 − x²	This equation appears to have all the parts of a quadratic equation, but it will require some manipulation before you can use reverse-FOIL.
	First, subtract 31 from both sides, and add x² to both sides, so that the expression is set equal to zero.
	Now rearrange and combine the terms, so that the equation has the form ax² + bx + c = 0.
	Now you’re ready to perform reverse-FOIL. What are the factors of 35? 1 35 5 7 One of those factors will be negative, since the third term is negative. If so, which two numbers listed above can have the product of −35 and a difference of +2? −5 +7
	Therefore, x = 5 or −7.

Inequalities

Solve inequalities in the same way you have solved equations. Isolate the variable that you are solving for on one side of the equation and put everything else on the other side of the equation. However, when you have solved an inequality, your solution will typically be a range of values rather than a single value. Study the example below.

Question	Analysis
Solve for a: 4a + 6 > 2a + 10
4a − 2a + 6 > 10	Subtract 2a from both sides.
4a − 2a > 10 − 6	Subtract 6 from both sides.
2a > 4	Combine like terms.
a > 2	Divide both sides by 2.

In this example, the range of possible values of a are all numbers larger than 2. That is, a can be any value greater than 2 but cannot equal 2. Most of the math for inequalities is the same as if you were solving an equation. There is, however, one crucial difference between solving equations and inequalities. When you multiply or divide an inequality by a negative number, you must change the direction of the inequality sign. So for example, when you divide both sides of the inequality −5a > 10 by −5 to isolate a, you change the direction of the sign: a < −2. Because of this rule, you cannot multiply or divide both sides of an inequality by a variable, since you do not know whether the variable has a positive or negative value.

To understand why this is so, consider this example, which uses integers:

1 < 2

If you multiply both sides by −1:

−1 ? −2

Which is greater? The number −1 is greater than −2, so you need to use a greater than sign:

−1 > −2

The inequality sign has flipped. You can test the previous example, in which a is less than −2, by plugging in a couple of numbers. Plug in −3 for a, and you’ll find that (−5)(−3) > 10 becomes 15 > 10, a true statement. Plug in a number greater than −2, say 0, and you’ll find that (−5)(0) > 10 becomes 0 > 10, which is not a true statement. Only by flipping the inequality sign do you get the correct answer.

Try an inequality question on your own. This question does not have answer choices. Express your answer as an inequality.

Solve for z:

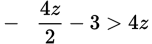
Explanation

Step 1: You are given an inequality.

Step 2: You are asked to solve for the variable, z.

Step 3: First, simplify the fraction:

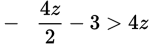
−2z − 3 > 4z

Isolate z on one side of the inequality by adding 2z to both sides:

−3 > 6z

Divide both sides by 6:

If this were Test Day, you might see the correct answer stated that way, or it might be reversed, like this:

Step 4: Double-check your math. Be sure to check that you used all of the appropriate signs.

Classic Quadratic	Example
(x + y)(x − y) = x² − y²	(x + 3)(x − 3) = x² − 9
(x + y)² = x² + 2xy + y²	(a + 4)² = a² + 8a + 16
(x − y)² = x² − 2xy + y²	(y − 6)² = y² − 12y + 36

x > 2	x is greater than 2.
x < −1	x is less than −1.
x − 2	x is greater than or equal to 2.
x ≤ −1	x is less than or equal to −1.