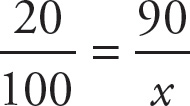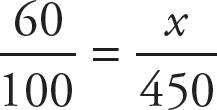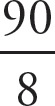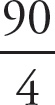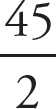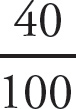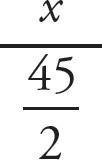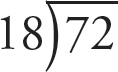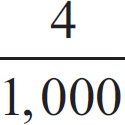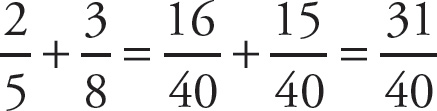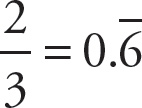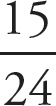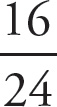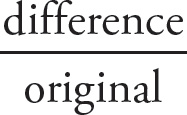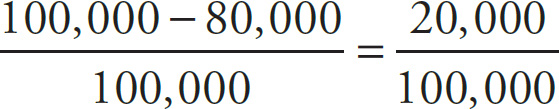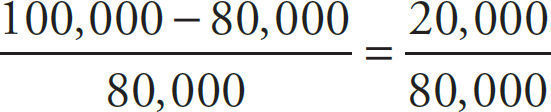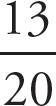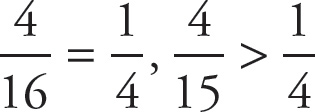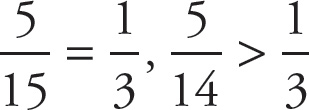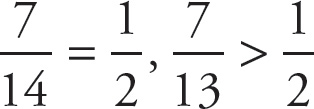Fractions, Decimals, and Percents: Answers and Explanations
ANSWER KEY
SSAT Fractions, Decimals, and Percents Drill 1
SSAT Fractions, Decimals, and Percents Drill 1
1. B

 Compare the decimal values for each fraction in the answers to the decimal value of
Compare the decimal values for each fraction in the answers to the decimal value of 
 , 0.375. Only choice (B), with a value of 0.357, is less.
, 0.375. Only choice (B), with a value of 0.357, is less.

 As
As 
 is less than a half, first look to see which fraction are not less than a half. In fact, they all are. However, most of the fractions are fairly close to a half, while choice (B) is closer to one-third. As it is the smallest fraction, it must be the correct answer.
is less than a half, first look to see which fraction are not less than a half. In fact, they all are. However, most of the fractions are fairly close to a half, while choice (B) is closer to one-third. As it is the smallest fraction, it must be the correct answer.
2. C

 Translate the English into a mathematical equation, replacing of with a multiplication sign and is with an equal sign.
Translate the English into a mathematical equation, replacing of with a multiplication sign and is with an equal sign. 
 .
.
3. A

 Add the three fractions, first converting each to the lowest common denominator 60:
Add the three fractions, first converting each to the lowest common denominator 60: 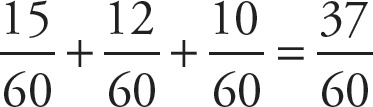
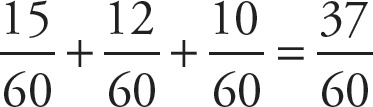 .
.
4. B

 Fractions represent a part to a whole, while ratios represent a part to a part. As the ratio of girls to boys is 8 to 4, the fraction of girls is
Fractions represent a part to a whole, while ratios represent a part to a part. As the ratio of girls to boys is 8 to 4, the fraction of girls is 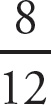
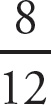 , or
, or 
 . It is useful to know that
. It is useful to know that 
 as a percent rounds to 67. You can also set up the proportion to determine the percent:
as a percent rounds to 67. You can also set up the proportion to determine the percent: 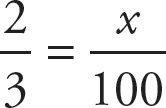
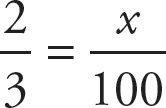 .
.
5. D

 First take 30% of $450: $450 ×
First take 30% of $450: $450 × 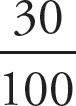
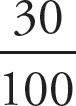 = $135. As the question asks for the remaining amount, subtract $135 from $450: $315.
= $135. As the question asks for the remaining amount, subtract $135 from $450: $315.
6. B

 Set up a proportion:
Set up a proportion: 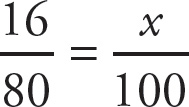
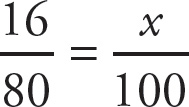 . Cross multiply: 1600 = 80x. Divide both sides by 80: x = 20.
. Cross multiply: 1600 = 80x. Divide both sides by 80: x = 20.

 Translate the English into a mathematical equation, replacing is with an equal sign, what percent with
Translate the English into a mathematical equation, replacing is with an equal sign, what percent with 
 , and of with a multiplication sign. 16 =
, and of with a multiplication sign. 16 = 
 × 80, and solve for x = 20.
× 80, and solve for x = 20.
7. D

 Three thousand five is represented by 3,005. Twelve thousandths is represented by 0.012.
Three thousand five is represented by 3,005. Twelve thousandths is represented by 0.012.
8. D

 Set up the division:
Set up the division: 
 . Move the decimals:
. Move the decimals: 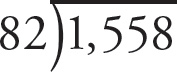
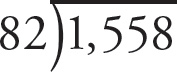 . As two times 82 is greater than 155, start with a 1 over the second 5, multiply by 82, find the difference, bring down the 8, and determine how many times 82 goes into 738:
. As two times 82 is greater than 155, start with a 1 over the second 5, multiply by 82, find the difference, bring down the 8, and determine how many times 82 goes into 738:

 Set up a fraction and move the decimals:
Set up a fraction and move the decimals: 
 . Reduce by 2:
. Reduce by 2: 
 . As 41 × 10 is 410, we know the result must be (D) or (E). Test choice (D): 41 × 19 = 779.
. As 41 × 10 is 410, we know the result must be (D) or (E). Test choice (D): 41 × 19 = 779.
9. B

 First determine how much 12 golf balls weigh: 12 × 0.045 = 0.54. Then, subtract that weight from the combined weight of the bag and the 12 balls for the weight of the bag: 0.62 – 0.54 = 0.08 kilograms.
First determine how much 12 golf balls weigh: 12 × 0.045 = 0.54. Then, subtract that weight from the combined weight of the bag and the 12 balls for the weight of the bag: 0.62 – 0.54 = 0.08 kilograms.
10. E

 Stack the numbers so that the decimals are aligned. Then add normally. The result is 826.
Stack the numbers so that the decimals are aligned. Then add normally. The result is 826.
SSAT Fractions, Decimals, and Percents Drill 2
1. C

 A ratio represents a part to a part, although in this case the question is asking for a comparison of a part to a whole (usually called a fraction). As there are 20 vegetables and onions, the ratio of onions to vegetables is 2:20, or 1:10.
A ratio represents a part to a part, although in this case the question is asking for a comparison of a part to a whole (usually called a fraction). As there are 20 vegetables and onions, the ratio of onions to vegetables is 2:20, or 1:10.
2. D

 Convert the hours to minutes for an apples to apples comparison: 2 hours = 120 minutes. Thus, the ratio of 48 minutes to 120 minutes is 48:120, which reduces to 2:5.
Convert the hours to minutes for an apples to apples comparison: 2 hours = 120 minutes. Thus, the ratio of 48 minutes to 120 minutes is 48:120, which reduces to 2:5.
3. B

 A ratio represents a part to a part, while a fraction represents a part to a whole. As 18 games were lost out of totally of 27 played, 9 games won. Thus, the ratio of wins to losses is 9:18 or 1:2.
A ratio represents a part to a part, while a fraction represents a part to a whole. As 18 games were lost out of totally of 27 played, 9 games won. Thus, the ratio of wins to losses is 9:18 or 1:2.
4. E

 Calculate the total amount of snow by adding all of the values in the table. Add the inches, aligning by the decimal. Over 8 hours, it snowed 23.8 inches.
Calculate the total amount of snow by adding all of the values in the table. Add the inches, aligning by the decimal. Over 8 hours, it snowed 23.8 inches.

 Take advantage of the question’s invitation to estimate. Start by adding up only the numbers to the left of the decimal. You already have 20 inches, and you have not included the decimal values. Thus, the total snow must be greater than 20, leaving only choice (E).
Take advantage of the question’s invitation to estimate. Start by adding up only the numbers to the left of the decimal. You already have 20 inches, and you have not included the decimal values. Thus, the total snow must be greater than 20, leaving only choice (E).
5. C

 First, to find the number, set up a proportion, cross multiply, and divide by 20:
First, to find the number, set up a proportion, cross multiply, and divide by 20: 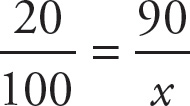
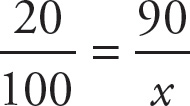 , 20x = 9,000, and x = 450. Then find the answer by following the same procedure:
, 20x = 9,000, and x = 450. Then find the answer by following the same procedure: 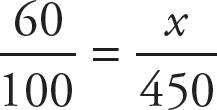
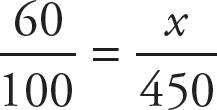 , 100x = 27,000, and x = 270.
, 100x = 27,000, and x = 270.

 You can use logic. 60% of a number is three times greater than 20% of the number. Thus, simply multiply 90 by 3.
You can use logic. 60% of a number is three times greater than 20% of the number. Thus, simply multiply 90 by 3.
6. C

 Let x represent the value of the original crop. As he first sold 30%, he had 70% left, so he currently has 0.70x. He then sold 10% of that remaining amount, so he had 90% of the amount left. Therefore, he now has (0.90)(0.70)x. Multiply the two numbers for a result of 0.63x. This is 63% of the original amount.
Let x represent the value of the original crop. As he first sold 30%, he had 70% left, so he currently has 0.70x. He then sold 10% of that remaining amount, so he had 90% of the amount left. Therefore, he now has (0.90)(0.70)x. Multiply the two numbers for a result of 0.63x. This is 63% of the original amount.

 On percent questions without an original amount, you can plug in for the original amount. 100 is a good number. If the farmer sold 30% of his corn, he sold 30, leaving 70. If he then sold 10% of what is left, he sold 7. There are 63 left, or 63% of the original 100.
On percent questions without an original amount, you can plug in for the original amount. 100 is a good number. If the farmer sold 30% of his corn, he sold 30, leaving 70. If he then sold 10% of what is left, he sold 7. There are 63 left, or 63% of the original 100.
7. C

 Set up a proportion to solve for x, cross multiply, and divide by 80:
Set up a proportion to solve for x, cross multiply, and divide by 80: 
 , 900 = 80x, and x =
, 900 = 80x, and x = 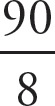
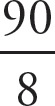 or
or 
 . The next proportion calls for 2x, which is
. The next proportion calls for 2x, which is 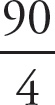
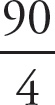 or
or 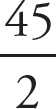
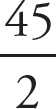 . Follow the same procedure:
. Follow the same procedure: 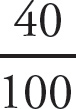
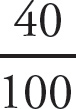 or
or 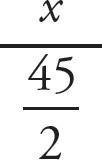
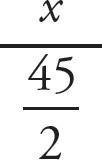 , 900 = 100x, and x = 9.
, 900 = 100x, and x = 9.

 If you cut a percent in half and double the number, the result will be the same.
If you cut a percent in half and double the number, the result will be the same.
8. D

 Convert the feet into inches, so you can easily divide: 6
Convert the feet into inches, so you can easily divide: 6 
 feet is 6 feet and 4 inches, and 6 feet is 72 inches. So, you have 76 inches. Divide 76 by 4 to determine how many pieces will result.
feet is 6 feet and 4 inches, and 6 feet is 72 inches. So, you have 76 inches. Divide 76 by 4 to determine how many pieces will result.
9. D

 When you multiply by 1,000 you move the decimal over three places to the right. Thus, 0.050 × 1,000.00 = 50.
When you multiply by 1,000 you move the decimal over three places to the right. Thus, 0.050 × 1,000.00 = 50.
10. B

 Set up long division, and move the decimals:
Set up long division, and move the decimals: 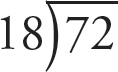
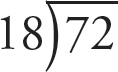 . Determine how many times 18 goes into 72. The answer is 4 without a remainder. Translate the English into a mathematical expression, replacing the quotient with a division sign. 7.2 ÷ 1.8 = 4.
. Determine how many times 18 goes into 72. The answer is 4 without a remainder. Translate the English into a mathematical expression, replacing the quotient with a division sign. 7.2 ÷ 1.8 = 4.

 Put 7.2 over 1.8, move the decimals, and reduce in steps:
Put 7.2 over 1.8, move the decimals, and reduce in steps: 
 = 4.
= 4.
ISEE Fractions, Decimals, and Percents Drill 1
1. B

 Choice (A) is the same as
Choice (A) is the same as 
 , as you can move the two decimals. Choice (D) reduces to
, as you can move the two decimals. Choice (D) reduces to 
 . If you divide 6 into 5, you will get a repeating decimal, consistent with choice (C). As the decimal in choice (B) terminates, the value is not equal to
. If you divide 6 into 5, you will get a repeating decimal, consistent with choice (C). As the decimal in choice (B) terminates, the value is not equal to 
 .
.

 Numbers divided by 3, 6, 7, and 9 generate repeating decimals. If you know this fact, you can select choice (B) without additional work.
Numbers divided by 3, 6, 7, and 9 generate repeating decimals. If you know this fact, you can select choice (B) without additional work.
2. D

 Multiply 1,200 by 0.45 and add the result to 1,200, for a total of 1,740.
Multiply 1,200 by 0.45 and add the result to 1,200, for a total of 1,740.

 A 45% increase is slightly less than an increase by half. An increase by half would add 600 followers for a total of 1,800. Thus, the answer must be a bit less than 1,800. Choice (D) is the only option.
A 45% increase is slightly less than an increase by half. An increase by half would add 600 followers for a total of 1,800. Thus, the answer must be a bit less than 1,800. Choice (D) is the only option.
3. C

 Convert each fraction to a decimal or create common denominators for the fractions, so you can compare the numerators. Choice (C) is the largest.
Convert each fraction to a decimal or create common denominators for the fractions, so you can compare the numerators. Choice (C) is the largest.

 Notice that the numerators in choices (A), (B), and (D) are less than half of their denominators, which means each fraction is something less than one-half. In choice (C), the numerator is greater than half of its denominator, which means that it is something greater than one-half.
Notice that the numerators in choices (A), (B), and (D) are less than half of their denominators, which means each fraction is something less than one-half. In choice (C), the numerator is greater than half of its denominator, which means that it is something greater than one-half.
4. C

 Assign x and y to the lengths of the rectangle. The original rectangle has an area of xy. If you add 20% to the length x, you will have a length of 1.2x. If you reduce the length y by 40%, you will have a length of 0.6y. Thus, the new area will be 0.72xy, meaning the area was reduced by 0.28 or 28%.
Assign x and y to the lengths of the rectangle. The original rectangle has an area of xy. If you add 20% to the length x, you will have a length of 1.2x. If you reduce the length y by 40%, you will have a length of 0.6y. Thus, the new area will be 0.72xy, meaning the area was reduced by 0.28 or 28%.

 Plug in values for the length and width of the rectangle. Because a square is a type of rectangle and 10 is a great number for percent questions, use 10 for the length and width. The original area is 100. The larger side (20% greater than 10) is now 12 and the smaller side (40% reduction from 10) is now 6. Thus, the new area is 72, meaning there was a decrease of 28. As the original area was 100, 28 out of 100 is 28%.
Plug in values for the length and width of the rectangle. Because a square is a type of rectangle and 10 is a great number for percent questions, use 10 for the length and width. The original area is 100. The larger side (20% greater than 10) is now 12 and the smaller side (40% reduction from 10) is now 6. Thus, the new area is 72, meaning there was a decrease of 28. As the original area was 100, 28 out of 100 is 28%.
5. C

 4.2 + 5.6 = 9.8. As 0.8 is equivalent to
4.2 + 5.6 = 9.8. As 0.8 is equivalent to 
 , the answer is 9
, the answer is 9 
 .
.
6. D

 The digit 4 is in the thousandths place, which means its value is
The digit 4 is in the thousandths place, which means its value is 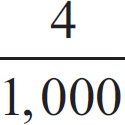
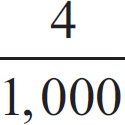 .
.
7. D

 Set up a proportion and cross multiply:
Set up a proportion and cross multiply: 
 , so x = 150.
, so x = 150.

 Translate English into Math. Is means =, what means x (variable), and of means (times), so 9 =
Translate English into Math. Is means =, what means x (variable), and of means (times), so 9 = 
 × 6. Thus, x = 150.
× 6. Thus, x = 150.
8. A

 To obtain the discount, or amount saved, multiply $12 by 40% or 0.4. The result is $4.80.
To obtain the discount, or amount saved, multiply $12 by 40% or 0.4. The result is $4.80.
9. A

 Stack the decimals and work carefully when borrowing tens. 11.25 – 4.67 = 6.58.
Stack the decimals and work carefully when borrowing tens. 11.25 – 4.67 = 6.58.
10. D

 To find the number halfway between two fractions, you should find the average of the fractions. You will need to create a common denominator to add the fractions:
To find the number halfway between two fractions, you should find the average of the fractions. You will need to create a common denominator to add the fractions: 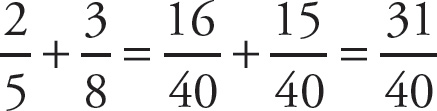
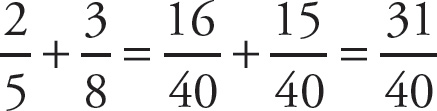 . Now, you can divide the sum by 2:
. Now, you can divide the sum by 2: 
 .
.
ISEE Fractions, Decimals, and Percents Drill 2
1. A

 The September price of $1.25/lb rose after a 10% increase in October to $1.38/lb, after rounding up: 0.10 × $1.25 = $0.125, and $1.25 + $0.125 = $1.375 ($1.38). In November, the price dropped after a 10% decrease to $1.24/lb, after rounding down: 0.10 × $1.38 = $0.138, and $1.38 – $0.138 = $1.242 ($1.24).
The September price of $1.25/lb rose after a 10% increase in October to $1.38/lb, after rounding up: 0.10 × $1.25 = $0.125, and $1.25 + $0.125 = $1.375 ($1.38). In November, the price dropped after a 10% decrease to $1.24/lb, after rounding down: 0.10 × $1.38 = $0.138, and $1.38 – $0.138 = $1.242 ($1.24).

 In this type of question, the original price does not matter, so plug in $100 to keep things simple. Adding 10% brings the price to $110. Subtracting 10% brings the price to $99. Thus, increasing a price by a percent and then decreasing the price by the same percent will yield a price lower than the original amount.
In this type of question, the original price does not matter, so plug in $100 to keep things simple. Adding 10% brings the price to $110. Subtracting 10% brings the price to $99. Thus, increasing a price by a percent and then decreasing the price by the same percent will yield a price lower than the original amount.
2. B

 Convert both fractions to decimals:
Convert both fractions to decimals: 
 = 0.625.
= 0.625. 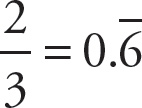
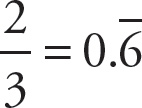 . Alternatively, create common denominators:
. Alternatively, create common denominators: 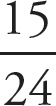
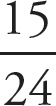 and
and 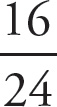
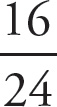 .
.
3. C

 10% of 100 = 10 (0.10 × 100 = 10), and 20% of 50 = 10 (0.20 × 50 = 10).
10% of 100 = 10 (0.10 × 100 = 10), and 20% of 50 = 10 (0.20 × 50 = 10).

 If you double the percent (10% to 20%) and halve the amount (100 to 50), the result will be the same.
If you double the percent (10% to 20%) and halve the amount (100 to 50), the result will be the same.
4. B

 A negative closer to 0 is larger than one farther away.
A negative closer to 0 is larger than one farther away.
5. B

 Percent change is calculated as follows:
Percent change is calculated as follows: 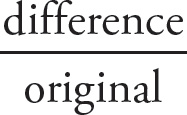
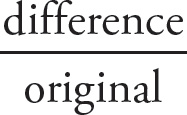 × 100, so the house value decreased by 20%.
× 100, so the house value decreased by 20%. 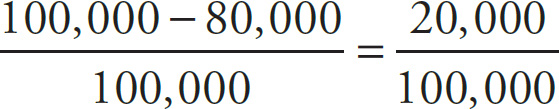
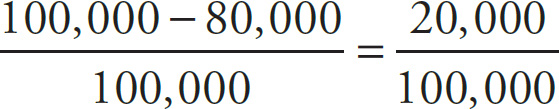 × 100 = 20%.
× 100 = 20%.
6. A

 Percent change is calculated as follows:
Percent change is calculated as follows: 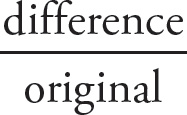
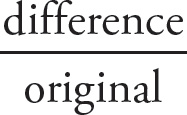 × 100, so the house value increased by 25%.
× 100, so the house value increased by 25%. 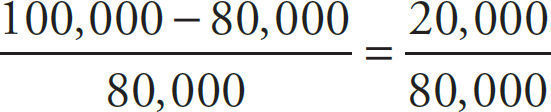
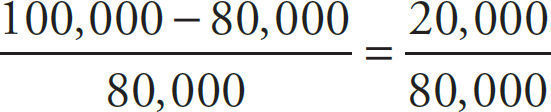 × 100 = 25%.
× 100 = 25%.
7. C

 Reduce the fraction in Column A in steps and stages:
Reduce the fraction in Column A in steps and stages: 
 = 3
= 3

 To make reducing easier, move the decimal over by one in the numerator and by one in the denominator:
To make reducing easier, move the decimal over by one in the numerator and by one in the denominator: 
 .
.
8. B

 Convert Column A to a decimal for the comparison:
Convert Column A to a decimal for the comparison: 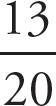
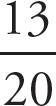 = 0.65.
= 0.65.
9. B

 You can add the fractions in each column by finding the common denominator for each column, but this will be terribly difficult for Column B. You can also convert each fraction into a decimal before adding them, which will make Column B a bit easier to deal with.
You can add the fractions in each column by finding the common denominator for each column, but this will be terribly difficult for Column B. You can also convert each fraction into a decimal before adding them, which will make Column B a bit easier to deal with.

 This question is much easier if you think creatively about the fractions. As
This question is much easier if you think creatively about the fractions. As 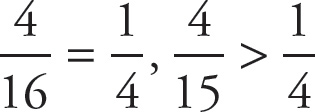
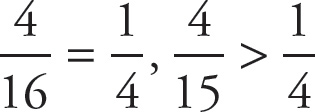 . Similarly, as
. Similarly, as 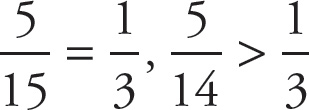
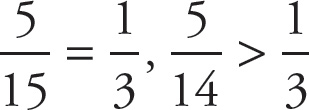 . Likewise, as
. Likewise, as 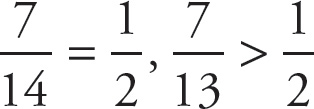
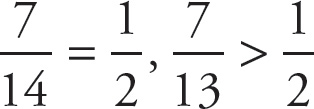 . Thus, the sum of the fractions in Column B is greater than the sum of the fractions in Column A.
. Thus, the sum of the fractions in Column B is greater than the sum of the fractions in Column A.
10. B

 The TV is discounted by 10% first: 0.10 × $400 = $40, and $400 – $40 = $360. The tax is calculated on the sale price: 0.10 × $360 = $36, and $360 + $36 = $396.
The TV is discounted by 10% first: 0.10 × $400 = $40, and $400 – $40 = $360. The tax is calculated on the sale price: 0.10 × $360 = $36, and $360 + $36 = $396.

 In this type of question, the original price does not matter, so plug in $100 to keep things simple. Subtracting 10% brings the price to $90. Adding 10% brings the price to $99. Thus, decreasing a price by a percent and then increasing the price by the same percent will yield a price lower than the original amount.
In this type of question, the original price does not matter, so plug in $100 to keep things simple. Subtracting 10% brings the price to $90. Adding 10% brings the price to $99. Thus, decreasing a price by a percent and then increasing the price by the same percent will yield a price lower than the original amount.

 Compare the decimal values for each fraction in the answers to the decimal value of
Compare the decimal values for each fraction in the answers to the decimal value of 
![]() , 0.375. Only choice (B), with a value of 0.357, is less.
, 0.375. Only choice (B), with a value of 0.357, is less.
 As
As 
![]() is less than a half, first look to see which fraction are not less than a half. In fact, they all are. However, most of the fractions are fairly close to a half, while choice (B) is closer to one-third. As it is the smallest fraction, it must be the correct answer.
is less than a half, first look to see which fraction are not less than a half. In fact, they all are. However, most of the fractions are fairly close to a half, while choice (B) is closer to one-third. As it is the smallest fraction, it must be the correct answer.
 Translate the English into a mathematical equation, replacing of with a multiplication sign and is with an equal sign.
Translate the English into a mathematical equation, replacing of with a multiplication sign and is with an equal sign. 
 .
.
 Add the three fractions, first converting each to the lowest common denominator 60:
Add the three fractions, first converting each to the lowest common denominator 60: 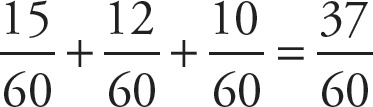
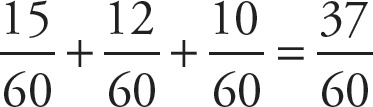 .
.
 Fractions represent a part to a whole, while ratios represent a part to a part. As the ratio of girls to boys is 8 to 4, the fraction of girls is
Fractions represent a part to a whole, while ratios represent a part to a part. As the ratio of girls to boys is 8 to 4, the fraction of girls is 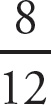
![]() , or
, or 
![]() . It is useful to know that
. It is useful to know that 
![]() as a percent rounds to 67. You can also set up the proportion to determine the percent:
as a percent rounds to 67. You can also set up the proportion to determine the percent: 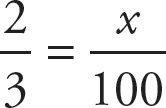
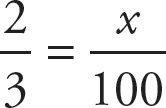 .
.
 First take 30% of $450: $450 ×
First take 30% of $450: $450 × 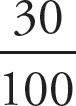
![]() = $135. As the question asks for the remaining amount, subtract $135 from $450: $315.
= $135. As the question asks for the remaining amount, subtract $135 from $450: $315.
 Set up a proportion:
Set up a proportion: 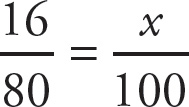
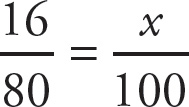 . Cross multiply: 1600 = 80x. Divide both sides by 80: x = 20.
. Cross multiply: 1600 = 80x. Divide both sides by 80: x = 20.
 Translate the English into a mathematical equation, replacing is with an equal sign, what percent with
Translate the English into a mathematical equation, replacing is with an equal sign, what percent with 
![]() , and of with a multiplication sign. 16 =
, and of with a multiplication sign. 16 = 
![]() × 80, and solve for x = 20.
× 80, and solve for x = 20.
 Three thousand five is represented by 3,005. Twelve thousandths is represented by 0.012.
Three thousand five is represented by 3,005. Twelve thousandths is represented by 0.012.
 Set up the division:
Set up the division: 
![]() . Move the decimals:
. Move the decimals: 
![]() . As two times 82 is greater than 155, start with a 1 over the second 5, multiply by 82, find the difference, bring down the 8, and determine how many times 82 goes into 738:
. As two times 82 is greater than 155, start with a 1 over the second 5, multiply by 82, find the difference, bring down the 8, and determine how many times 82 goes into 738: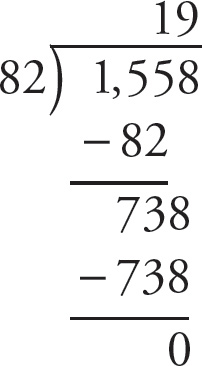
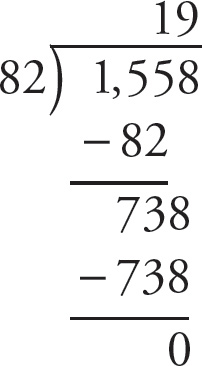

 Set up a fraction and move the decimals:
Set up a fraction and move the decimals: 
 . Reduce by 2:
. Reduce by 2: 
![]() . As 41 × 10 is 410, we know the result must be (D) or (E). Test choice (D): 41 × 19 = 779.
. As 41 × 10 is 410, we know the result must be (D) or (E). Test choice (D): 41 × 19 = 779.
 First determine how much 12 golf balls weigh: 12 × 0.045 = 0.54. Then, subtract that weight from the combined weight of the bag and the 12 balls for the weight of the bag: 0.62 – 0.54 = 0.08 kilograms.
First determine how much 12 golf balls weigh: 12 × 0.045 = 0.54. Then, subtract that weight from the combined weight of the bag and the 12 balls for the weight of the bag: 0.62 – 0.54 = 0.08 kilograms.
 Stack the numbers so that the decimals are aligned. Then add normally. The result is 826.
Stack the numbers so that the decimals are aligned. Then add normally. The result is 826.