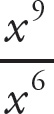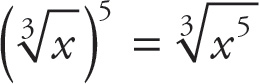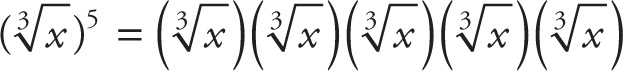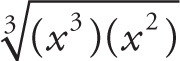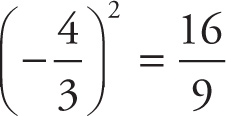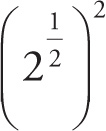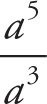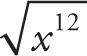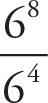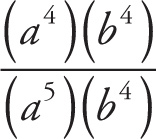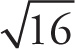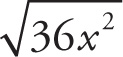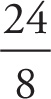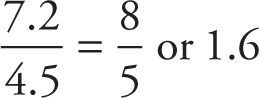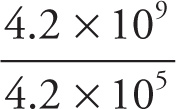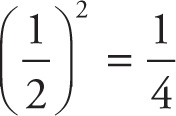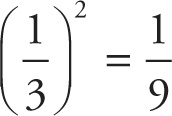Exponents and Roots: Answers and Explanations
ANSWER KEY
SSAT Exponents and Roots Drill 1
SSAT Exponents and Roots Drill 1
1. A

 To simplify a cube root, find any cubes and remove them. x3 appears twice within x8, so you can pull out x2. There will still be two x values under the root, so leave x2 there: (x2)
To simplify a cube root, find any cubes and remove them. x3 appears twice within x8, so you can pull out x2. There will still be two x values under the root, so leave x2 there: (x2)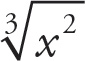
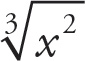 .
.

 You can expand the expressions out. x8 becomes (x)(x)(x)(x)(x)(x)(x)(x). As we are dealing with cubes, combine the x terms to (x3)(x3)(x2). Therefore, there are two cubes to remove from the cube root (each one becoming x), and x2 is left behind. Outside of the radical, all roots are multiplied. Thus, (x2)
You can expand the expressions out. x8 becomes (x)(x)(x)(x)(x)(x)(x)(x). As we are dealing with cubes, combine the x terms to (x3)(x3)(x2). Therefore, there are two cubes to remove from the cube root (each one becoming x), and x2 is left behind. Outside of the radical, all roots are multiplied. Thus, (x2)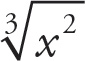
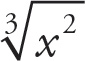 .
.
2. C

 Simplify the number terms first.
Simplify the number terms first. 
 . Simplify the variables, using the rules of exponents: When like bases are divided, subtract the exponents.
. Simplify the variables, using the rules of exponents: When like bases are divided, subtract the exponents. 
 = f3−2 = f;
= f3−2 = f; 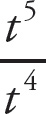
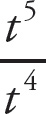 = t5−4 = t;
= t5−4 = t; 
 = u1−1 = 1. This yields
= u1−1 = 1. This yields 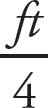
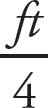 .
.
3. E

 Cube the numerator and the denominator. Remember that the cube of a negative base will be negative.
Cube the numerator and the denominator. Remember that the cube of a negative base will be negative. 
 .
.
4. C

 Replace the variables in the expression with the values provided. 3(6) – (42) = 18 – 16 = 2.
Replace the variables in the expression with the values provided. 3(6) – (42) = 18 – 16 = 2.
5. D

 Solve for the variables by applying the rules of exponents. When an exponential expression is raised to another power, multiply the exponents. Therefore, (xa)3 = x3a = x15. Therefore, 3a = 15, and a = 5. When exponential expressions with like bases are divided, subtract the exponents. Therefore,
Solve for the variables by applying the rules of exponents. When an exponential expression is raised to another power, multiply the exponents. Therefore, (xa)3 = x3a = x15. Therefore, 3a = 15, and a = 5. When exponential expressions with like bases are divided, subtract the exponents. Therefore, 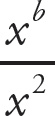
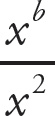 = xb−2 = x7. Therefore, b – 2 = 7, and b = 9. 9 – 5 = 4.
= xb−2 = x7. Therefore, b – 2 = 7, and b = 9. 9 – 5 = 4.
6. D

 Any number (other than 0) raised to a power of 0 is 1. Therefore, the value of the expression is 3.
Any number (other than 0) raised to a power of 0 is 1. Therefore, the value of the expression is 3.
7. B

 When a fraction between 0 and 1 is raised to a power greater than 1, the fraction becomes smaller. Likewise, when a root is taken of a fraction between 0 and 1, the fraction becomes larger. Thus, x2 < x <
When a fraction between 0 and 1 is raised to a power greater than 1, the fraction becomes smaller. Likewise, when a root is taken of a fraction between 0 and 1, the fraction becomes larger. Thus, x2 < x < 
 .
.

 Plug in a number for x. If x =
Plug in a number for x. If x = 
 , then
, then 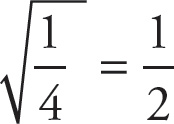
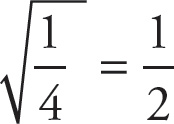 , and
, and 
 . Only choice (B) provides the correct range of the values.
. Only choice (B) provides the correct range of the values.
8. B

 Multiply the number terms inside the scientific notation first: 2.4 × 3.0 = 7.2. Multiply the exponential expressions with a base of ten. With like bases, add the exponents when you multiply the bases. (10x)(10y) = 10x + y.
Multiply the number terms inside the scientific notation first: 2.4 × 3.0 = 7.2. Multiply the exponential expressions with a base of ten. With like bases, add the exponents when you multiply the bases. (10x)(10y) = 10x + y.
9. E

 Expand the scientific notation: 4.0 × 103 = 4,000. Add to 100,000 for a total of 104,000.
Expand the scientific notation: 4.0 × 103 = 4,000. Add to 100,000 for a total of 104,000.
10. B

 You can multiply roots together, even if the numbers under the roots are different. Thus,
You can multiply roots together, even if the numbers under the roots are different. Thus, 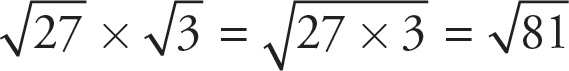
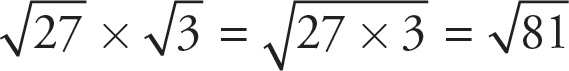 = 9.
= 9.
SSAT Exponents and Roots Drill 2
1. D

 The power applies to everything within the parentheses. A negative number raised to an odd power yields an odd result: (–2)3 = –8. When exponential expressions are raised to a power, multiply the exponents. Thus, (x2)3 = x6, and (y5)3 = y15.
The power applies to everything within the parentheses. A negative number raised to an odd power yields an odd result: (–2)3 = –8. When exponential expressions are raised to a power, multiply the exponents. Thus, (x2)3 = x6, and (y5)3 = y15.
2. D

 Replace the variables in the expression with the values provided and calculate. (52)(2) – (5)(22) + (2 × 5)2 = 50 – 20 + 100 = 130.
Replace the variables in the expression with the values provided and calculate. (52)(2) – (5)(22) + (2 × 5)2 = 50 – 20 + 100 = 130.
3. B

 Start with the numerator. The power applies to all terms within the parentheses. Deal with the number first: 23 = 8. When exponential expressions are raised to a power, multiply the exponents. Thus, (x3)3 = x9, and (y2)3 = y6. Now address the denominator, starting with the numbers:
Start with the numerator. The power applies to all terms within the parentheses. Deal with the number first: 23 = 8. When exponential expressions are raised to a power, multiply the exponents. Thus, (x3)3 = x9, and (y2)3 = y6. Now address the denominator, starting with the numbers: 
 = 2. When exponential expressions with the same base are divided, subtract the exponents:
= 2. When exponential expressions with the same base are divided, subtract the exponents: 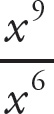
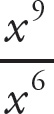 = x9−6 = x3, and
= x9−6 = x3, and 
 = y6−9 = y−3.
= y6−9 = y−3.
4. A

 According to PEMDAS, you can move the exponent under the root:
According to PEMDAS, you can move the exponent under the root: 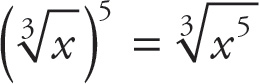
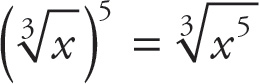 . There is one x3 included in x5, so you can pull that out as x. Remaining under the root is x2 :
. There is one x3 included in x5, so you can pull that out as x. Remaining under the root is x2 : 
 .
.

 You can expand out the expression:
You can expand out the expression: 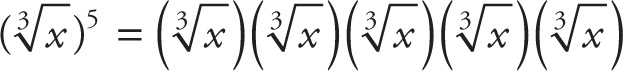
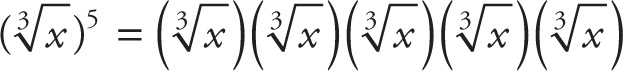 , or
, or 
 . This can be expressed as
. This can be expressed as 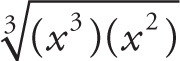
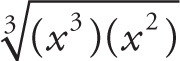 . Therefore, there is one cube to remove from the cube root, but x2 is left behind:
. Therefore, there is one cube to remove from the cube root, but x2 is left behind: 

5. C

 The exponent applies to the numerator and denominator. A negative term raised to any even power will yield a positive result. Thus,
The exponent applies to the numerator and denominator. A negative term raised to any even power will yield a positive result. Thus, 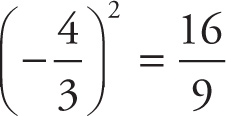
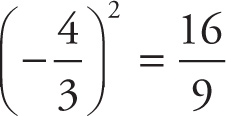 .
.
6. C

 As you cannot combine a square root and a cube root, simplify the different roots first:
As you cannot combine a square root and a cube root, simplify the different roots first: 
 = 2, and
= 2, and 
 = 8. 2 × 8 = 16.
= 8. 2 × 8 = 16.
7. B

 First, raise the term within the parentheses to a power of 3. (ab)3 = a3b3. When you divide exponential expressions with the same base, subtract the exponents.
First, raise the term within the parentheses to a power of 3. (ab)3 = a3b3. When you divide exponential expressions with the same base, subtract the exponents. 
 = a3−3 = a0, and
= a3−3 = a0, and 
 = b3−4 = b−1 or
= b3−4 = b−1 or 
 . As any number other than 0 raised to a power of 0 equals 1, a0 = 1, and c0 = 1.
. As any number other than 0 raised to a power of 0 equals 1, a0 = 1, and c0 = 1.
8. E

 Replace the variables in the expression with the values provided and calculate. (–4)(–42) = (–4)(16) = –64.
Replace the variables in the expression with the values provided and calculate. (–4)(–42) = (–4)(16) = –64.
9. B

 When exponential terms are raised to a power, multiply the exponents.
When exponential terms are raised to a power, multiply the exponents. 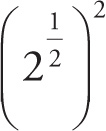
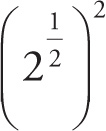 = 21 = 2. Thus, 5 × 2 = 10.
= 21 = 2. Thus, 5 × 2 = 10.
10. A

 When you divide exponential expressions with the same base, subtract the exponents.
When you divide exponential expressions with the same base, subtract the exponents. 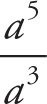
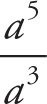 = a5−3 = a2, and
= a5−3 = a2, and 
 = b14−6 = b8.
= b14−6 = b8.
ISEE Exponents and Roots Drill 1
1. B

 The exponential terms in the parentheses can’t be simplified, so solve them: 22 = 4, 23 = 8, and 4 + 8 = 12. Simplify the resulting fraction to
The exponential terms in the parentheses can’t be simplified, so solve them: 22 = 4, 23 = 8, and 4 + 8 = 12. Simplify the resulting fraction to 
 .
.

 Remember to divide before you multiply when dealing with fractions. Reducing first avoids large products.
Remember to divide before you multiply when dealing with fractions. Reducing first avoids large products.
2. C

 Convert each term to a decimal before adding them: 3 × 106 = 5,300,000 and 6.2 × 104 = 62,000. Stack them by their digits correctly to get the sum of 5,362,000, which is 5.362 × 106.
Convert each term to a decimal before adding them: 3 × 106 = 5,300,000 and 6.2 × 104 = 62,000. Stack them by their digits correctly to get the sum of 5,362,000, which is 5.362 × 106.
3. D

 The square root of 36 is 6. For the variable, you must use the rules of exponents. If the bases are the same, add the exponents when you multiply the terms. The term x12 represents a base of x that was squared, i.e., multiplied by itself. Thus the two exponents added were the same value and produced a sum of 12. (x6)(x6) = x12. To find the square root, divide the exponent in half.
The square root of 36 is 6. For the variable, you must use the rules of exponents. If the bases are the same, add the exponents when you multiply the terms. The term x12 represents a base of x that was squared, i.e., multiplied by itself. Thus the two exponents added were the same value and produced a sum of 12. (x6)(x6) = x12. To find the square root, divide the exponent in half. 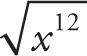
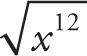 = x6.
= x6.

 The square root of an exponent will be one-half of the exponent.
The square root of an exponent will be one-half of the exponent.
4. B

 The terms in the numerator and denominator have the same base, so follow the rules of exponents. Subtract the exponents when the terms are divided.
The terms in the numerator and denominator have the same base, so follow the rules of exponents. Subtract the exponents when the terms are divided. 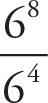
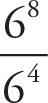 = 64.
= 64.
5. D

 Follow the rules of exponents. The power applies to all terms inside the parentheses. A negative base raised to an even power like 4 produces a positive result, in this case 16. When an exponential term is raised to a power, multiply the exponents. (x2)4 = x8 and (y3)4 = y12.
Follow the rules of exponents. The power applies to all terms inside the parentheses. A negative base raised to an even power like 4 produces a positive result, in this case 16. When an exponential term is raised to a power, multiply the exponents. (x2)4 = x8 and (y3)4 = y12.
6. B

 Simplify 813 to a base of 3 so the terms have the same base. 81 = 34 so 813 = (34)3. When an exponential term is raised to a power, multiply the exponents. (34)3 = 312. Thus, x = 12.
Simplify 813 to a base of 3 so the terms have the same base. 81 = 34 so 813 = (34)3. When an exponential term is raised to a power, multiply the exponents. (34)3 = 312. Thus, x = 12.
7. C

 Any base to the zero power equals 1. So c0 = 1, so c will not appear in the simplified answer. When an exponential term is raised to a power, multiply the exponents. The power applies to both terms inside the parentheses. (ab)4 = (a4)(b4). With like bases, subtract the exponents when the terms are divided.
Any base to the zero power equals 1. So c0 = 1, so c will not appear in the simplified answer. When an exponential term is raised to a power, multiply the exponents. The power applies to both terms inside the parentheses. (ab)4 = (a4)(b4). With like bases, subtract the exponents when the terms are divided. 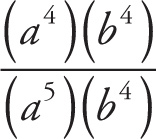
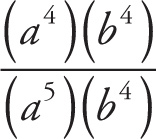 = a−1 or
= a−1 or 
 .
.
8. A

 Simplify the roots first.
Simplify the roots first. 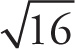
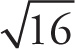 = 4,
= 4, 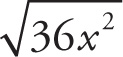
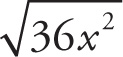 = 6x, and
= 6x, and 
 = 8. Terms that are unlike (4 and 6x) can’t be added. Reduce.
= 8. Terms that are unlike (4 and 6x) can’t be added. Reduce. 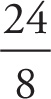
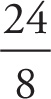 to 3. Last, distribute the 3 by multiplying it by 4 and 6x to get a product of 12 + 18x.
to 3. Last, distribute the 3 by multiplying it by 4 and 6x to get a product of 12 + 18x.
9. D

 How many times tells you to divide. 2.5 × 104 = 25,000 and 5.0 × 101 = 50. The result is 500, which is 5.0 × 102.
How many times tells you to divide. 2.5 × 104 = 25,000 and 5.0 × 101 = 50. The result is 500, which is 5.0 × 102.
10. B


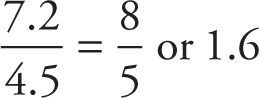
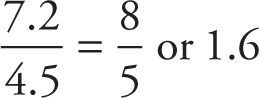 . When dividing exponential terms with like bases, subtract the exponents.
. When dividing exponential terms with like bases, subtract the exponents. 
 = 108, and the final simplified form equals 1.6 × 108.
= 108, and the final simplified form equals 1.6 × 108.

 All of the answer choices contain 1.6, so it is not necessary to solve that value, although you do need to determine whether the result will require moving the decimal to maintain scientific notation. If you see that the result will maintain scientific notation, all you need to do is focus on the exponent.
All of the answer choices contain 1.6, so it is not necessary to solve that value, although you do need to determine whether the result will require moving the decimal to maintain scientific notation. If you see that the result will maintain scientific notation, all you need to do is focus on the exponent.
ISEE Exponents and Roots Drill 2
1. B

 With like bases, add the exponents when the terms are multiplied. (10x)(10y) = 10x + y. The product of the two numerical terms, 8.0 and 6.0 equals 48. However, 48 must be expressed as 4.8 × 101 in scientific notation. Because this requires multiplying the exponents again, add the 1 to the exponent: 10x + y + 1.
With like bases, add the exponents when the terms are multiplied. (10x)(10y) = 10x + y. The product of the two numerical terms, 8.0 and 6.0 equals 48. However, 48 must be expressed as 4.8 × 101 in scientific notation. Because this requires multiplying the exponents again, add the 1 to the exponent: 10x + y + 1.

 You can plug in values for x and y. If x and y are both set to 2, you have 800 × 600 = 480,000. Choice (B) matches.
You can plug in values for x and y. If x and y are both set to 2, you have 800 × 600 = 480,000. Choice (B) matches.
2. A

 Column A: 1.5 × 105 + 2.6 × 10–3 = 150,000 + 0.0026 = 150,000.0026. Column B: 9.8 × 104 + 8.7 × 10–2 = 98,000 + 0.087 = 98,000.087.
Column A: 1.5 × 105 + 2.6 × 10–3 = 150,000 + 0.0026 = 150,000.0026. Column B: 9.8 × 104 + 8.7 × 10–2 = 98,000 + 0.087 = 98,000.087.

 The negative exponents will have minimal effect. Raising 10 to the fifth power results in a greater value than does raising 10 to the fourth power.
The negative exponents will have minimal effect. Raising 10 to the fifth power results in a greater value than does raising 10 to the fourth power.
3. A

 Column A: (6.0 × 102)(7.0 × 102) = 42 × 104 = 4.2 × 105. Column B:
Column A: (6.0 × 102)(7.0 × 102) = 42 × 104 = 4.2 × 105. Column B: 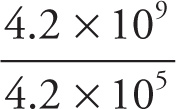
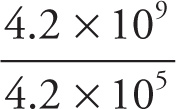 = 1 × 104, or just 104.
= 1 × 104, or just 104.
4. D

 It is not possible to know which column is greater, because x does not have to increase when squared. It could remain the same (0 or 1) or become smaller (a fraction between 0 and 1).
It is not possible to know which column is greater, because x does not have to increase when squared. It could remain the same (0 or 1) or become smaller (a fraction between 0 and 1).

 Plug in an easy number for x, such as 2. In this case, Column B is greater, which means that Column A is not always greater and that the two columns are not always equal. Eliminate (A) and (C). Now try x = 0. The two columns are not equal, which means Column B is not always greater. Eliminate (B).
Plug in an easy number for x, such as 2. In this case, Column B is greater, which means that Column A is not always greater and that the two columns are not always equal. Eliminate (A) and (C). Now try x = 0. The two columns are not equal, which means Column B is not always greater. Eliminate (B).
5. A

 Simplify both columns, following the rules of exponents. When dividing like bases, subtract the exponents. When multiplying like bases, add the exponents. Column A equals 220 and Column B equals 29.
Simplify both columns, following the rules of exponents. When dividing like bases, subtract the exponents. When multiplying like bases, add the exponents. Column A equals 220 and Column B equals 29.
6. C

 Create a common base by changing 27 to 33 : (33)5. When a power is raised to a power, multiply the exponents: 315.
Create a common base by changing 27 to 33 : (33)5. When a power is raised to a power, multiply the exponents: 315.
7. A

 A decimal gets smaller when raised to a positive power greater than 1. The greater the exponent with respect to a particular decimal, the smaller the result.
A decimal gets smaller when raised to a positive power greater than 1. The greater the exponent with respect to a particular decimal, the smaller the result.

 If you are not sure what happens to decimals raised to a power, try a simple fraction (decimals and fractions are the same), such as
If you are not sure what happens to decimals raised to a power, try a simple fraction (decimals and fractions are the same), such as 
 . As
. As 
 , and
, and 
 , you can see that the larger the exponent, the smaller the result.
, you can see that the larger the exponent, the smaller the result.
8. A

 A fraction gets smaller when raised to a positive power greater than 1. The smaller the fraction with respect to a particular exponent, the smaller the result.
A fraction gets smaller when raised to a positive power greater than 1. The smaller the fraction with respect to a particular exponent, the smaller the result.

 If you are not sure what happens to fractions raised to a power, try simple fractions such as
If you are not sure what happens to fractions raised to a power, try simple fractions such as 
 and
and 
 . As
. As 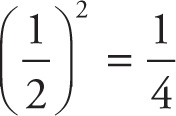
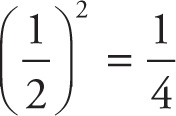 , and
, and 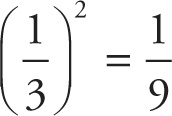
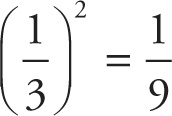 , you can see that the smaller the fraction, the smaller the result.
, you can see that the smaller the fraction, the smaller the result.
9. A

 A fraction gets larger when the square root is taken. The larger the fraction, the larger the result.
A fraction gets larger when the square root is taken. The larger the fraction, the larger the result.
10. B

 Any number greater than 1 gets smaller when the square root is taken, including numbers greater than 1 with fractions or decimals. The smaller the number, the smaller the result.
Any number greater than 1 gets smaller when the square root is taken, including numbers greater than 1 with fractions or decimals. The smaller the number, the smaller the result.

 To simplify a cube root, find any cubes and remove them. x3 appears twice within x8, so you can pull out x2. There will still be two x values under the root, so leave x2 there: (x2)
To simplify a cube root, find any cubes and remove them. x3 appears twice within x8, so you can pull out x2. There will still be two x values under the root, so leave x2 there: (x2)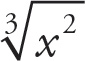
![]() .
.
 You can expand the expressions out. x8 becomes (x)(x)(x)(x)(x)(x)(x)(x). As we are dealing with cubes, combine the x terms to (x3)(x3)(x2). Therefore, there are two cubes to remove from the cube root (each one becoming x), and x2 is left behind. Outside of the radical, all roots are multiplied. Thus, (x2)
You can expand the expressions out. x8 becomes (x)(x)(x)(x)(x)(x)(x)(x). As we are dealing with cubes, combine the x terms to (x3)(x3)(x2). Therefore, there are two cubes to remove from the cube root (each one becoming x), and x2 is left behind. Outside of the radical, all roots are multiplied. Thus, (x2)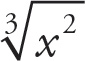
![]() .
.
 Simplify the number terms first.
Simplify the number terms first. 
 . Simplify the variables, using the rules of exponents: When like bases are divided, subtract the exponents.
. Simplify the variables, using the rules of exponents: When like bases are divided, subtract the exponents. 
![]() = f3−2 = f;
= f3−2 = f; 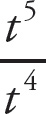
![]() = t5−4 = t;
= t5−4 = t; 
![]() = u1−1 = 1. This yields
= u1−1 = 1. This yields 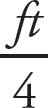
![]() .
.
 Cube the numerator and the denominator. Remember that the cube of a negative base will be negative.
Cube the numerator and the denominator. Remember that the cube of a negative base will be negative. 
 .
.
 Replace the variables in the expression with the values provided. 3(6) – (42) = 18 – 16 = 2.
Replace the variables in the expression with the values provided. 3(6) – (42) = 18 – 16 = 2.
 Solve for the variables by applying the rules of exponents. When an exponential expression is raised to another power, multiply the exponents. Therefore, (xa)3 = x3a = x15. Therefore, 3a = 15, and a = 5. When exponential expressions with like bases are divided, subtract the exponents. Therefore,
Solve for the variables by applying the rules of exponents. When an exponential expression is raised to another power, multiply the exponents. Therefore, (xa)3 = x3a = x15. Therefore, 3a = 15, and a = 5. When exponential expressions with like bases are divided, subtract the exponents. Therefore, 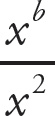
![]() = xb−2 = x7. Therefore, b – 2 = 7, and b = 9. 9 – 5 = 4.
= xb−2 = x7. Therefore, b – 2 = 7, and b = 9. 9 – 5 = 4.
 Any number (other than 0) raised to a power of 0 is 1. Therefore, the value of the expression is 3.
Any number (other than 0) raised to a power of 0 is 1. Therefore, the value of the expression is 3.
 When a fraction between 0 and 1 is raised to a power greater than 1, the fraction becomes smaller. Likewise, when a root is taken of a fraction between 0 and 1, the fraction becomes larger. Thus, x2 < x <
When a fraction between 0 and 1 is raised to a power greater than 1, the fraction becomes smaller. Likewise, when a root is taken of a fraction between 0 and 1, the fraction becomes larger. Thus, x2 < x < 
![]() .
.
 Plug in a number for x. If x =
Plug in a number for x. If x = 
![]() , then
, then 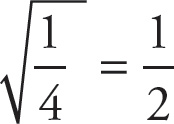
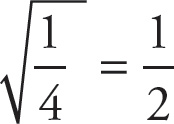 , and
, and 
 . Only choice (B) provides the correct range of the values.
. Only choice (B) provides the correct range of the values.
 Multiply the number terms inside the scientific notation first: 2.4 × 3.0 = 7.2. Multiply the exponential expressions with a base of ten. With like bases, add the exponents when you multiply the bases. (10x)(10y) = 10x + y.
Multiply the number terms inside the scientific notation first: 2.4 × 3.0 = 7.2. Multiply the exponential expressions with a base of ten. With like bases, add the exponents when you multiply the bases. (10x)(10y) = 10x + y.
 Expand the scientific notation: 4.0 × 103 = 4,000. Add to 100,000 for a total of 104,000.
Expand the scientific notation: 4.0 × 103 = 4,000. Add to 100,000 for a total of 104,000.
 You can multiply roots together, even if the numbers under the roots are different. Thus,
You can multiply roots together, even if the numbers under the roots are different. Thus, 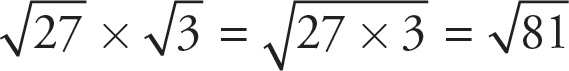
![]() = 9.
= 9.