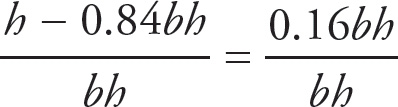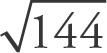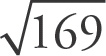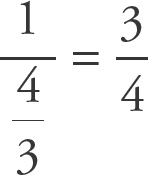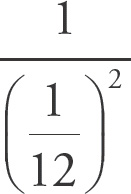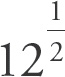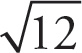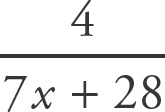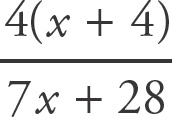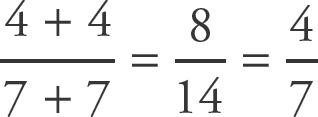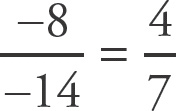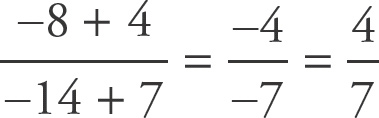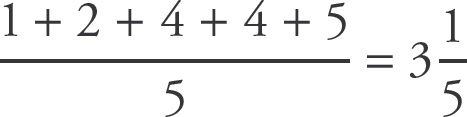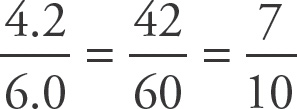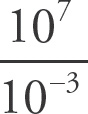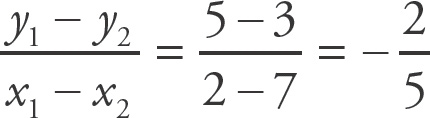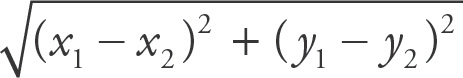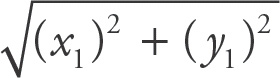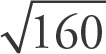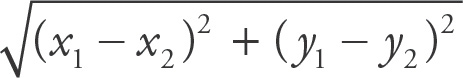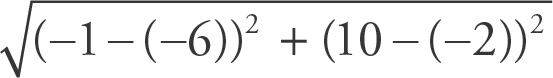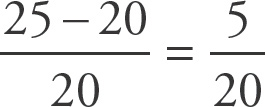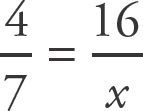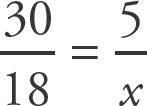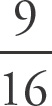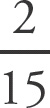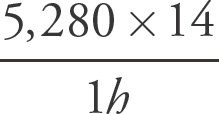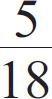ISEE Practice Test: Answers and Explanations
ANSWER KEY
Section 1
Section 1
1. B

 To liberate is to free something.
To liberate is to free something.
2. A

 Tangible means touchable or concrete.
Tangible means touchable or concrete.
3. B

 Innate means inborn or native.
Innate means inborn or native.
4. C

 To deliberate is to consider or reflect.
To deliberate is to consider or reflect.
5. D

 Pious means virtuous or sacred.
Pious means virtuous or sacred.
6. D

 To plea is to request.
To plea is to request.

 The word please shares the same root.
The word please shares the same root.
7. D

 To disperse is to scatter.
To disperse is to scatter.
8. B

 Renown means fame.
Renown means fame.
9. C

 To venerate is to respect.
To venerate is to respect.
10. D

 To plunder is to steal.
To plunder is to steal.
11. C

 Voracious means having a huge appetite or gluttonous.
Voracious means having a huge appetite or gluttonous.
12. A

 Belligerent means argumentative.
Belligerent means argumentative.

 The Latin root bell means war. The period before the Civil War is called the ante-bellum period. The word rebel comes from the same root.
The Latin root bell means war. The period before the Civil War is called the ante-bellum period. The word rebel comes from the same root.
13. D

 Ominous means worrisome.
Ominous means worrisome.
14. C

 Zealous means passionate.
Zealous means passionate.
15. A

 A benediction is a blessing.
A benediction is a blessing.

 The Latin root bene means good, and the root dict means word, so a benediction is a good word, a blessing.
The Latin root bene means good, and the root dict means word, so a benediction is a good word, a blessing.
16. D

 Disparate means unequal.
Disparate means unequal.

 The Latin root dis means not, and the root par means equal.
The Latin root dis means not, and the root par means equal.
17. A

 Aggrandize means exaggerate.
Aggrandize means exaggerate.
18. A

 To distinguish is to separate or differentiate.
To distinguish is to separate or differentiate.
19. A

 Equivocal means ambiguous.
Equivocal means ambiguous.

 The Latin root equ means equal, and the root voc means voice, so equivocal means equal voiced, which is to say ambiguous in meaning.
The Latin root equ means equal, and the root voc means voice, so equivocal means equal voiced, which is to say ambiguous in meaning.
20. B

 A malcontent is a grouch.
A malcontent is a grouch.

 The Latin root mal means bad.
The Latin root mal means bad.
21. A

 Utter sorrow requires anguish (suffering) as the answer.
Utter sorrow requires anguish (suffering) as the answer.

 Even if you do not know the word anguish, you can eliminate the other answers because the correct answer must mean utter sorrow.
Even if you do not know the word anguish, you can eliminate the other answers because the correct answer must mean utter sorrow.
22. A

 Years of practice and lacks the tremendous talent requires adept (able) as the answer.
Years of practice and lacks the tremendous talent requires adept (able) as the answer.

 Even if you do not know the word adept, you can eliminate the other answers because the correct answer must reflect the result of years of lessons yet without tremendous talent.
Even if you do not know the word adept, you can eliminate the other answers because the correct answer must reflect the result of years of lessons yet without tremendous talent.
23. C

 Did not realize I was making an accusation requires insinuate (hint) as the answer.
Did not realize I was making an accusation requires insinuate (hint) as the answer.

 Even if you do not know the word insinuate, you can eliminate the other answers because the correct answer must reflect that the speaker made an accusation that the listener did not realize was an accusation.
Even if you do not know the word insinuate, you can eliminate the other answers because the correct answer must reflect that the speaker made an accusation that the listener did not realize was an accusation.
24. B

 Showered his friends with gifts and gave his time requires generous as the answer.
Showered his friends with gifts and gave his time requires generous as the answer.
25. B

 Enthusiasm and positive attitude never require diminished.
Enthusiasm and positive attitude never require diminished.
26. B

 False doctrine and injustice require ignoble (shameful) as the answer.
False doctrine and injustice require ignoble (shameful) as the answer.

 Even if you do not know the word ignoble, you can eliminate choices (A) and (C), as well as choice (D) if you know the word, because the correct answer must reflect false doctrine and injustice.
Even if you do not know the word ignoble, you can eliminate choices (A) and (C), as well as choice (D) if you know the word, because the correct answer must reflect false doctrine and injustice.
27. D

 Naive and unlikely, believe, and true require ruse (trick) as the answer.
Naive and unlikely, believe, and true require ruse (trick) as the answer.

 Even if you do not know the word ruse, you can eliminate choices (A) and (C), as well as choice (B) if you know it, because the correct answer must reflect that Matthew is naive and will believe unlikely things are true.
Even if you do not know the word ruse, you can eliminate choices (A) and (C), as well as choice (B) if you know it, because the correct answer must reflect that Matthew is naive and will believe unlikely things are true.
28. C

 Could not be resolved requires impasse (stalemate or deadlock) as the answer.
Could not be resolved requires impasse (stalemate or deadlock) as the answer.

 Even if you do not know the word impasse, you can eliminate choices (B) and (D), as well as choice (A) if you know it, because the correct answer must reflect that an issue could not be resolved.
Even if you do not know the word impasse, you can eliminate choices (B) and (D), as well as choice (A) if you know it, because the correct answer must reflect that an issue could not be resolved.
29. B

 Always in high spirits requires jubilant (joyous) as the answer.
Always in high spirits requires jubilant (joyous) as the answer.

 Even if you do not know the word jubilant, you can eliminate choice (A), as well as choices (C) and (D) if you know them, because the correct answer must reflect always in high spirits. You may need to guess from three choices.
Even if you do not know the word jubilant, you can eliminate choice (A), as well as choices (C) and (D) if you know them, because the correct answer must reflect always in high spirits. You may need to guess from three choices.
30. C

 Activities of dancers requires kinetic (relating to motion) as the answer.
Activities of dancers requires kinetic (relating to motion) as the answer.

 Even if you do not know the word kinetic, you can eliminate the other answers because the correct answer must reflect activity of dancers.
Even if you do not know the word kinetic, you can eliminate the other answers because the correct answer must reflect activity of dancers.
31. C

 Both blanks must relate to could speak powerfully and expressively, thus requiring eloquence (well spoken) and verbalize as the answer.
Both blanks must relate to could speak powerfully and expressively, thus requiring eloquence (well spoken) and verbalize as the answer.

 Do one blank at a time. The first blank, which might seem easier, must reflect that the sister could speak powerfully and expressively, so you can eliminate choices (A), (B), and (D). The second blank must also relate to could speak powerfully and expressively. The Latin root loc/loq means speech.
Do one blank at a time. The first blank, which might seem easier, must reflect that the sister could speak powerfully and expressively, so you can eliminate choices (A), (B), and (D). The second blank must also relate to could speak powerfully and expressively. The Latin root loc/loq means speech.
32. D

 The first blank must mean believe, while the second blank must mean praises, thus requiring suppose and extol (praise) as the answer.
The first blank must mean believe, while the second blank must mean praises, thus requiring suppose and extol (praise) as the answer.

 Do one blank at a time. The second blank, which might seem easier, must mean praise, so you can eliminate choices (A), (B), and (C). The first blank must mean believe.
Do one blank at a time. The second blank, which might seem easier, must mean praise, so you can eliminate choices (A), (B), and (C). The first blank must mean believe.
33. D

 The first blank must mean bad, while the second blank must mean confirmed, thus requiring maladroit (clumsy or unskilled) and perpetuated (continued) as the answer.
The first blank must mean bad, while the second blank must mean confirmed, thus requiring maladroit (clumsy or unskilled) and perpetuated (continued) as the answer.

 Do one blank at a time. The first blank, which might seem easier, must reflect unable to do anything, so you can eliminate choices (B) and (C). The first blank must mean confirmed, so you can eliminate choice (A). The Latin root mal means bad, and adroit means skilled.
Do one blank at a time. The first blank, which might seem easier, must reflect unable to do anything, so you can eliminate choices (B) and (C). The first blank must mean confirmed, so you can eliminate choice (A). The Latin root mal means bad, and adroit means skilled.
34. A

 The first blank must be the opposite of nasty, while the second blank must reflect how the parents reacted to bad news, thus requiring benign (kindness) and chagrin (irritation) as the answer.
The first blank must be the opposite of nasty, while the second blank must reflect how the parents reacted to bad news, thus requiring benign (kindness) and chagrin (irritation) as the answer.

 Do one blank at a time. The first blank, which might seem easier, must be the opposite of nasty, so you can eliminate choice (B), as well as choice (D) if you know it. The second blank must reflect how the parents reacted to bad news, so you can eliminate choice (C). You may need to guess between choices (A) and (C). The Latin root ben means good.
Do one blank at a time. The first blank, which might seem easier, must be the opposite of nasty, so you can eliminate choice (B), as well as choice (D) if you know it. The second blank must reflect how the parents reacted to bad news, so you can eliminate choice (C). You may need to guess between choices (A) and (C). The Latin root ben means good.
35. B

 The first blank must be the opposite of lack of brevity, while the second blank must reflect an unsatisfied hope, thus requiring concisely (briefly) and undermining (weakening) as the answer.
The first blank must be the opposite of lack of brevity, while the second blank must reflect an unsatisfied hope, thus requiring concisely (briefly) and undermining (weakening) as the answer.

 Do one blank at a time. The first blank, which might seem easier if you know the word brevity (briefness), must be the opposite of brevity, so you can eliminate choices (A) and (C). If you don’t know brevity, you cannot eliminate any first-blank answers. The second blank must reflect an unsatisfied hope, so you can eliminate choice (D), as well as choice (A) if you haven’t eliminated it already. You may need to guess between choices (B) and (C).
Do one blank at a time. The first blank, which might seem easier if you know the word brevity (briefness), must be the opposite of brevity, so you can eliminate choices (A) and (C). If you don’t know brevity, you cannot eliminate any first-blank answers. The second blank must reflect an unsatisfied hope, so you can eliminate choice (D), as well as choice (A) if you haven’t eliminated it already. You may need to guess between choices (B) and (C).
36. C

 The first blank must mean hurtful, while the second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, thus requiring malicious (hateful) and ameliorate (improve) as the answer.
The first blank must mean hurtful, while the second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, thus requiring malicious (hateful) and ameliorate (improve) as the answer.

 Do one blank at a time. The first blank, which might seem easier, must mean hurtful, so you can eliminate choices (A) and (B). The second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, so you can eliminate choice (D). The Latin root mal means bad.
Do one blank at a time. The first blank, which might seem easier, must mean hurtful, so you can eliminate choices (A) and (B). The second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, so you can eliminate choice (D). The Latin root mal means bad.
37. C

 The first blank must emphasize Rodrigo’s efforts, while the second blank must reflect his goal as a loyal friend to end the rumors, thus requiring persistently (tirelessly) and dispel (end) as the answer.
The first blank must emphasize Rodrigo’s efforts, while the second blank must reflect his goal as a loyal friend to end the rumors, thus requiring persistently (tirelessly) and dispel (end) as the answer.

 Do one blank at a time. The second blank, which might seem easier, must reflect his goal as a loyal friend to end the rumors, so you can eliminate choices (B) and (D). The first blank must emphasize his efforts, so you can eliminate choice (A) if you know it. You may need to guess between choices (A) and (C). The Latin root ami means friend, and amiably means in a friendly way.
Do one blank at a time. The second blank, which might seem easier, must reflect his goal as a loyal friend to end the rumors, so you can eliminate choices (B) and (D). The first blank must emphasize his efforts, so you can eliminate choice (A) if you know it. You may need to guess between choices (A) and (C). The Latin root ami means friend, and amiably means in a friendly way.
38. B

 The first blank must reflect that Christopher received rare support, while the second blank must mean financial support, thus requiring fortunate and benefactor (supporter) as the answer.
The first blank must reflect that Christopher received rare support, while the second blank must mean financial support, thus requiring fortunate and benefactor (supporter) as the answer.

 Do one blank at a time. The first blank, which might seem easier, must reflect that Christopher received rare support, so you can eliminate choices (A) and (D). The second blank must mean financial support, so you can eliminate choice (C) if you know the word. You may need to guess between choices (B) and (C). The Latin root ben means good.
Do one blank at a time. The first blank, which might seem easier, must reflect that Christopher received rare support, so you can eliminate choices (A) and (D). The second blank must mean financial support, so you can eliminate choice (C) if you know the word. You may need to guess between choices (B) and (C). The Latin root ben means good.
39. A

 The first blank must mean clever, while the second blank must relate to a type of comment that is expressed, thus requiring astute (clever) and insights as the answer.
The first blank must mean clever, while the second blank must relate to a type of comment that is expressed, thus requiring astute (clever) and insights as the answer.

 Do one blank at a time. The first blank, which might seem easier, must mean clever, so you can eliminate choices (B) and (C) if you know the words. If not, you will have to rely entirely on the second blank. The second blank must relate to a type of comment that is expressed, so you can eliminate choice (B), as well as choice (D) if you know the word. You may need to guess.
Do one blank at a time. The first blank, which might seem easier, must mean clever, so you can eliminate choices (B) and (C) if you know the words. If not, you will have to rely entirely on the second blank. The second blank must relate to a type of comment that is expressed, so you can eliminate choice (B), as well as choice (D) if you know the word. You may need to guess.
40. B

 The first blank must reflect the swaying of low and high tides, while the second blank must mean vast separation, thus requiring fluctuated (swung) and chasm (vast divide) as the answer.
The first blank must reflect the swaying of low and high tides, while the second blank must mean vast separation, thus requiring fluctuated (swung) and chasm (vast divide) as the answer.

 Do one blank at a time. The first blank, which might seem easier, must reflect the swaying of low and high tides, so you can eliminate choices (A) and (C). The second blank must mean vast separation, so you can eliminate choice (D).
Do one blank at a time. The first blank, which might seem easier, must reflect the swaying of low and high tides, so you can eliminate choices (A) and (C). The second blank must mean vast separation, so you can eliminate choice (D).
Section 2
1. B

 If Blair is 6 years younger than Nate, who is n, she is n – 6.
If Blair is 6 years younger than Nate, who is n, she is n – 6.

 Plug in a value for n, such as n = 10. If Nate is 10, blair is 4. Only choice (B) yields 4 when you test 10.
Plug in a value for n, such as n = 10. If Nate is 10, blair is 4. Only choice (B) yields 4 when you test 10.
2. C

 To calculate the mean of all 5 scores, add the scores and divide by the number of scores: 320 + 75 = 395, and 395 ÷ 5 = 79.
To calculate the mean of all 5 scores, add the scores and divide by the number of scores: 320 + 75 = 395, and 395 ÷ 5 = 79.
3. C

 The extra distance is represented by the part of the walk from when he turned back to the beach through the time he reversed to go back home up until he arrived back at the point at which he had turned around in the first place. Read the chart, and you will see that from time 0.4 to time 0.6, he was moving closer to the beach. That distance was from 0.2 km (from 0.4 to 0.2). Getting back to where he first turned around adds another 0.2 km, for a total of 0.4 km.
The extra distance is represented by the part of the walk from when he turned back to the beach through the time he reversed to go back home up until he arrived back at the point at which he had turned around in the first place. Read the chart, and you will see that from time 0.4 to time 0.6, he was moving closer to the beach. That distance was from 0.2 km (from 0.4 to 0.2). Getting back to where he first turned around adds another 0.2 km, for a total of 0.4 km.
4. A

 A “weird symbol” defined to equal an equation is simply a different form of function notation, so plug in numbers as directed by the defined equation. As ‡x = 3x – 7, ‡6 = 3(6) – 7 = 18 – 7 = 11.
A “weird symbol” defined to equal an equation is simply a different form of function notation, so plug in numbers as directed by the defined equation. As ‡x = 3x – 7, ‡6 = 3(6) – 7 = 18 – 7 = 11.
5. C

 Choice (C) cannot be an integer because an even integer times any integer is even and that result plus an odd integer is odd. An odd number divided by 2 is not an integer.
Choice (C) cannot be an integer because an even integer times any integer is even and that result plus an odd integer is odd. An odd number divided by 2 is not an integer.

 Plug in an acceptable value for x, such as x = 4. Only choice (C) yields a non-integer when you test in 4.
Plug in an acceptable value for x, such as x = 4. Only choice (C) yields a non-integer when you test in 4.
6. A

 Let b represent the original base, and let h represent the original height. As area of a parallelogram is given by bh, the original area is bh. As the base was decreased by 30%, the new base will be 70% of the original, or 0.7b. As the height was increased by 20%, the new height will be 120% of the original, or 1.2h. Thus the new area is (7b)(1.2h) = 0.84bh. Percent change is found by taking the difference, dividing that by the original, and then multiplying the result by 100:
Let b represent the original base, and let h represent the original height. As area of a parallelogram is given by bh, the original area is bh. As the base was decreased by 30%, the new base will be 70% of the original, or 0.7b. As the height was increased by 20%, the new height will be 120% of the original, or 1.2h. Thus the new area is (7b)(1.2h) = 0.84bh. Percent change is found by taking the difference, dividing that by the original, and then multiplying the result by 100: 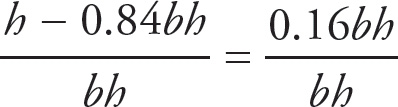
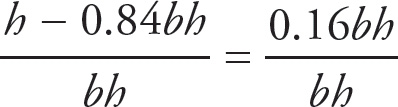 = 0.16, and 0.16 × 100 = 16.
= 0.16, and 0.16 × 100 = 16.

 As no original values were given, they do not matter, so you can plug in. Assign 10 to the original base and the original height. Thus, the original area was 100. The new base is 7 (reduced by 30% or 3), and the new height is 12 (increased by 20% or 2). Thus the new area is 84. As the new area is 16 lower than the original, and the original was 100, the percent change is 16.
As no original values were given, they do not matter, so you can plug in. Assign 10 to the original base and the original height. Thus, the original area was 100. The new base is 7 (reduced by 30% or 3), and the new height is 12 (increased by 20% or 2). Thus the new area is 84. As the new area is 16 lower than the original, and the original was 100, the percent change is 16.
7. C

 Use FOIL (First, Outside, Inside, Last) on the two factors: (x + 6)(x + 6) = (x2 + 6x + 6x + 36). Combine like terms: x2 + 12x + 36. Thus, n = 12.
Use FOIL (First, Outside, Inside, Last) on the two factors: (x + 6)(x + 6) = (x2 + 6x + 6x + 36). Combine like terms: x2 + 12x + 36. Thus, n = 12.

 Plug in a number for x, such as x = 2, and solve both sides of the equation: 82 = 4 + 2n + 36, so 64 = 40 + 2n. Combine like terms and divide by 2: n = 12.
Plug in a number for x, such as x = 2, and solve both sides of the equation: 82 = 4 + 2n + 36, so 64 = 40 + 2n. Combine like terms and divide by 2: n = 12.
8. B

 For a number to have a remainder when divided by 5, it must be some factor of 5 plus 4. So let a and b each equal 5x + 4. Substitute this expression into each answer. For choice (A), the result is 0, which is not equivalent to some factor of 5 plus 4. For choice (B), the result is 2(5x + 4) – (5x + 4), which is 10x + 8 – (5x + 4), which is 5x + 4. This is a factor of 5 plus 4. If you check choice (C) out of caution, the result is 2(5x + 4) + (5x + 4), which is 10x + 8 + (5x + 4), which is 15x + 12. When 12 is divided by 5, the remainder is 2, not 4. Choice (D) yields the same result as choice (C).
For a number to have a remainder when divided by 5, it must be some factor of 5 plus 4. So let a and b each equal 5x + 4. Substitute this expression into each answer. For choice (A), the result is 0, which is not equivalent to some factor of 5 plus 4. For choice (B), the result is 2(5x + 4) – (5x + 4), which is 10x + 8 – (5x + 4), which is 5x + 4. This is a factor of 5 plus 4. If you check choice (C) out of caution, the result is 2(5x + 4) + (5x + 4), which is 10x + 8 + (5x + 4), which is 15x + 12. When 12 is divided by 5, the remainder is 2, not 4. Choice (D) yields the same result as choice (C).

 If you are given a denominator of a quotient and a remainder, you can plug in for the numerator by adding the denominator and the remainder. In this case, you can set both a and b equal to 9 (4 + 5). Plug 9 into each answer (for a and b) and divide each answer by 5 to find its remainder. Only choice (B) yields a remainder of 4.
If you are given a denominator of a quotient and a remainder, you can plug in for the numerator by adding the denominator and the remainder. In this case, you can set both a and b equal to 9 (4 + 5). Plug 9 into each answer (for a and b) and divide each answer by 5 to find its remainder. Only choice (B) yields a remainder of 4.
9. C

 The sum of the integers from 1 to 497 will not include two numbers counted in the sum of all integers from 1 to 499, namely, 498 and 499. If the sum of all integers from 1 to 499 is r, then the sum of all integers from 1 to 497 will be r minus the sum of 498 and 499: r – (498 + 499), or r – 997.
The sum of the integers from 1 to 497 will not include two numbers counted in the sum of all integers from 1 to 499, namely, 498 and 499. If the sum of all integers from 1 to 499 is r, then the sum of all integers from 1 to 497 will be r minus the sum of 498 and 499: r – (498 + 499), or r – 997.
10. C

 Choice (D) cannot be true because under PEMDAS, you may not distribute the square root to each term under the square root. Rather, you must find the difference between the terms and then take the square root.
Choice (D) cannot be true because under PEMDAS, you may not distribute the square root to each term under the square root. Rather, you must find the difference between the terms and then take the square root.

 Guess and check to find out what could be true. For choice (A), as
Guess and check to find out what could be true. For choice (A), as 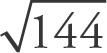
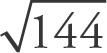 = 12, try to come up with a y value that will make the value under the square root equal to 144. Setting y equal to 5 works. Repeat the process for choice (B); in this case, setting y equal to 25 works. For choice (C),
= 12, try to come up with a y value that will make the value under the square root equal to 144. Setting y equal to 5 works. Repeat the process for choice (B); in this case, setting y equal to 25 works. For choice (C), 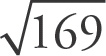
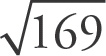 = 13, so setting y equal to 12 works. Select choice (C).
= 13, so setting y equal to 12 works. Select choice (C).
11. B

 Start with the parentheses and exponents:
Start with the parentheses and exponents: 
 . Now, cancel the denominator against 80: 2(2) = 4.
. Now, cancel the denominator against 80: 2(2) = 4.
12. C

 Set up a proportion:
Set up a proportion: 
 . Cross multiply: y? = 6 ×
. Cross multiply: y? = 6 × 
 y = 10y. Divide both sides by y: ? = 10.
y = 10y. Divide both sides by y: ? = 10.

 Plug in a value for y, such as y = 3. Now set up the proportion:
Plug in a value for y, such as y = 3. Now set up the proportion: 
 . Cross multiply and divide both sides by 3: ? = 10.
. Cross multiply and divide both sides by 3: ? = 10.
13. B

 First, list out Stewie’s integers: 5, 6, 7, 8, and 9. Now list out Peter’s integers: 6, 7, 8, 9, 10, and 11. Finally, circle any that are on both lists: 6, 7, 8, and 9.
First, list out Stewie’s integers: 5, 6, 7, 8, and 9. Now list out Peter’s integers: 6, 7, 8, 9, 10, and 11. Finally, circle any that are on both lists: 6, 7, 8, and 9.
14. D

 Multiply both sides of the second equation by –2: –4x –2y = –24. Stack the two equations on top of one another and combine like terms: –x = –16. Multiply both sides by –1: x = 16. Substitute 16 for x in either equation: 2(16) + y = 12. Combine like terms: y = –20. Finally, substitute the values for x and y in the expression and solve: 5(16) + (3)(–20) 80 – 60 = 20.
Multiply both sides of the second equation by –2: –4x –2y = –24. Stack the two equations on top of one another and combine like terms: –x = –16. Multiply both sides by –1: x = 16. Substitute 16 for x in either equation: 2(16) + y = 12. Combine like terms: y = –20. Finally, substitute the values for x and y in the expression and solve: 5(16) + (3)(–20) 80 – 60 = 20.

 Rather than solve the variables individually, stack the initial equations and combine like terms: 5x + 3y = 20. The question is asking for the value of 5x + 3y, so you are done.
Rather than solve the variables individually, stack the initial equations and combine like terms: 5x + 3y = 20. The question is asking for the value of 5x + 3y, so you are done.
15. A

 Adding 5 points to each student’s score will not affect the range because both the lowest and highest scores are 5 points higher, leaving the difference the same.
Adding 5 points to each student’s score will not affect the range because both the lowest and highest scores are 5 points higher, leaving the difference the same.
16. C

 The common quadratic (x + y)2 can be written as x2 + 2xy + y2. Rearrange the expression to x2 + y2 + 2xy and substitute in the given values: 65 + 2(28) = 65 + 56 + 121.
The common quadratic (x + y)2 can be written as x2 + 2xy + y2. Rearrange the expression to x2 + y2 + 2xy and substitute in the given values: 65 + 2(28) = 65 + 56 + 121.

 You can guess and check to find numbers that work. If xy = 28, then x and y can be 1 and 28, 2 and 14, or 4 and 7. Testing these in x2 + y2 shows that 4 and 7 work. Therefore, (x + y)2 = (4 + 7)2 = 121.
You can guess and check to find numbers that work. If xy = 28, then x and y can be 1 and 28, 2 and 14, or 4 and 7. Testing these in x2 + y2 shows that 4 and 7 work. Therefore, (x + y)2 = (4 + 7)2 = 121.
17. B

 If you unfold the cube, you will have a star above a plus sign and an X to the right of the plus sign. Only choice (B) provides this configuration.
If you unfold the cube, you will have a star above a plus sign and an X to the right of the plus sign. Only choice (B) provides this configuration.
18. A

 Choice (A) is correct because if a factor of one number is multiplied by a factor of another number, the product of the factors will be a factor of the product of the other two numbers.
Choice (A) is correct because if a factor of one number is multiplied by a factor of another number, the product of the factors will be a factor of the product of the other two numbers.

 Plug in values for all four variables, following the requirements. A proper set would be x = 5, c = 10, y = 3, and d = 6. Test each answer using these numbers. Only choice (A) is true.
Plug in values for all four variables, following the requirements. A proper set would be x = 5, c = 10, y = 3, and d = 6. Test each answer using these numbers. Only choice (A) is true.
19. A

 Set up an equation using the Pythagorean theorem: h2 + s2 = (2s)2. Distribute the exponent on the right and subtract s2 from both sides: h2 = 3s2. Take the square root of both sides: h = s
Set up an equation using the Pythagorean theorem: h2 + s2 = (2s)2. Distribute the exponent on the right and subtract s2 from both sides: h2 = 3s2. Take the square root of both sides: h = s
 .
.

 Plug in a value for s such as s = 2, and set up an equation using the Pythagorean theorem: h2 + 22 = 42. Apply the exponents and subtract 4 from both sides: h2 = 12. Take the square root of both sides and simplify the value under the square root sign: h =
Plug in a value for s such as s = 2, and set up an equation using the Pythagorean theorem: h2 + 22 = 42. Apply the exponents and subtract 4 from both sides: h2 = 12. Take the square root of both sides and simplify the value under the square root sign: h = 
 . Only choice (A) yields this value when you test 2 for s.
. Only choice (A) yields this value when you test 2 for s.
20. D

 Let x represent the number of purple marbles in the bag. Thus, there are 90 + x marbles in the bag. Set up an expression for the probability of selecting a purple marble:
Let x represent the number of purple marbles in the bag. Thus, there are 90 + x marbles in the bag. Set up an expression for the probability of selecting a purple marble: 
 . Set this fraction equal to the value of each answer, cross multiply, and solve for x. For choice (A), x = 10. For choice (B), x = 30. For choice (C), x = 60. Choice (D) does not yield an integer value.
. Set this fraction equal to the value of each answer, cross multiply, and solve for x. For choice (A), x = 10. For choice (B), x = 30. For choice (C), x = 60. Choice (D) does not yield an integer value.

 You can guess and check possible numbers of purple marbles, but this may be too time consuming. As an example, if you guess that there are 10 purple marbles, that would mean there are 100 marbles, and choice (A) would represent the probability of picking one of those 10 purple marbles.
You can guess and check possible numbers of purple marbles, but this may be too time consuming. As an example, if you guess that there are 10 purple marbles, that would mean there are 100 marbles, and choice (A) would represent the probability of picking one of those 10 purple marbles.
21. B

 The value of Column A is
The value of Column A is 
 . The value of column B is
. The value of column B is 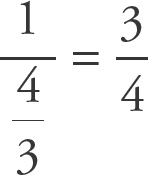
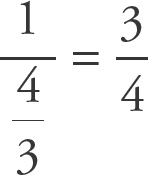 .
.
22. B

 Draw the figure, which is a right triangle. Column A represents the hypotenuse. Column B represents the sum of the two legs. The third side of a triangle must be less than the sum of the other two sides, so the value in Column B is greater.
Draw the figure, which is a right triangle. Column A represents the hypotenuse. Column B represents the sum of the two legs. The third side of a triangle must be less than the sum of the other two sides, so the value in Column B is greater.
23. D

 If y < 5, the value of Column A < 5(5) + 11, which is < 36. The value of Column B is < 6(5) + 6, which is < 36. As the value of both columns can be any number less than 36, the relative values cannot be determined.
If y < 5, the value of Column A < 5(5) + 11, which is < 36. The value of Column B is < 6(5) + 6, which is < 36. As the value of both columns can be any number less than 36, the relative values cannot be determined.

 Plug in a value for y, such as y = 2. The value of Column A is 21, and the value of Column B is 18. As the value of Column B is not always greater, and the values of the two columns are not always equal, eliminate choices (B) and (C). Now try y = 0. The value of Column A is 11, and the value of Column B is 6, so the value of Column A is still bigger. Try a negative number, such as y = –2. The value of Column A is 1, and the value of Column B is 6. As the value of Column A is not always greater, eliminate choice (A) and select choice (D).
Plug in a value for y, such as y = 2. The value of Column A is 21, and the value of Column B is 18. As the value of Column B is not always greater, and the values of the two columns are not always equal, eliminate choices (B) and (C). Now try y = 0. The value of Column A is 11, and the value of Column B is 6, so the value of Column A is still bigger. Try a negative number, such as y = –2. The value of Column A is 1, and the value of Column B is 6. As the value of Column A is not always greater, eliminate choice (A) and select choice (D).
24. A

 A negative exponent tells you to write the reciprocal of the base and bring the exponent to the denominator as a positive value. Thus, the value of Column A is
A negative exponent tells you to write the reciprocal of the base and bring the exponent to the denominator as a positive value. Thus, the value of Column A is 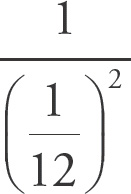
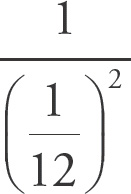 , and the value of Column B is
, and the value of Column B is 
 . When you divide 1 by a fraction, the fraction flips and comes to the numerator. Thus, the value of Column A is 122, and the value of Column A is
. When you divide 1 by a fraction, the fraction flips and comes to the numerator. Thus, the value of Column A is 122, and the value of Column A is 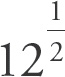
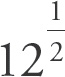 . Raising a number to a power of
. Raising a number to a power of 
 means taking the square root of that number. While you may not know the exact value of
means taking the square root of that number. While you may not know the exact value of 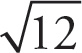
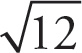 , it is less than 122 (144).
, it is less than 122 (144).
25. B

 When you need two separate probabilities to occur, you multiply the distinct probabilities (taking care to ensure that the probability of the second event assumes that the first event has occurred). Thus, the probability of picking two green buttons (Column A) is
When you need two separate probabilities to occur, you multiply the distinct probabilities (taking care to ensure that the probability of the second event assumes that the first event has occurred). Thus, the probability of picking two green buttons (Column A) is 
 . The probability of picking only one button is
. The probability of picking only one button is 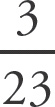
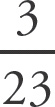 . This is all you need for Column B, because one button is sufficient, and the second pick doesn’t matter. Column B is greater because
. This is all you need for Column B, because one button is sufficient, and the second pick doesn’t matter. Column B is greater because 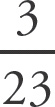
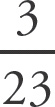 times any value between 0 and 1 will be less than
times any value between 0 and 1 will be less than 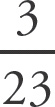
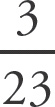 .
.

 Use logic. You need more luck to pick two green buttons than to pick one, which means there is a greater probability of picking one.
Use logic. You need more luck to pick two green buttons than to pick one, which means there is a greater probability of picking one.
26. C

 The value of Column A is
The value of Column A is 
 , as given. Finding the value of Column B requires a few steps. First, cross multiply the given equation: 7x = 4y. Now isolate one of the variables by dividing both sides by the number in front of that variable. If you isolate y, the result is y =
, as given. Finding the value of Column B requires a few steps. First, cross multiply the given equation: 7x = 4y. Now isolate one of the variables by dividing both sides by the number in front of that variable. If you isolate y, the result is y = 
 . Substitute
. Substitute 
 for y in Column B:
for y in Column B: 
 . Simplify first by creating a common denominator for the elements in the denominator:
. Simplify first by creating a common denominator for the elements in the denominator: 
 . Now further simplify the value in Column B by multiplying the numerator and denominator by the reciprocal of the denominator (which is
. Now further simplify the value in Column B by multiplying the numerator and denominator by the reciprocal of the denominator (which is 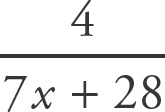
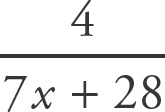 ):
): 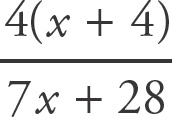
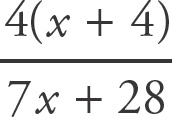 . Factor out a 7 from the denominator:
. Factor out a 7 from the denominator: 
 . Cancel out (x + 4):
. Cancel out (x + 4): 
 .
.

 Plug in values for x and y, such that the value of
Plug in values for x and y, such that the value of 
 . Good values would be x = 4, and y = 7. The value of Column A is
. Good values would be x = 4, and y = 7. The value of Column A is 
 , and the value of Column B is
, and the value of Column B is 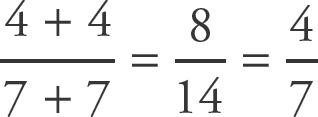
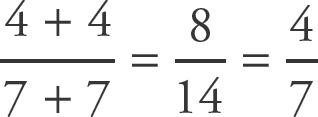 . As the value of Column A is not always greater than the value of Column B, and the value of Column B is not always greater than the value of Column A, eliminate choices (A) and (B). Now try different numbers, always making sure that
. As the value of Column A is not always greater than the value of Column B, and the value of Column B is not always greater than the value of Column A, eliminate choices (A) and (B). Now try different numbers, always making sure that 
 . Try x = –8, and y = –14. The value of Column A is
. Try x = –8, and y = –14. The value of Column A is 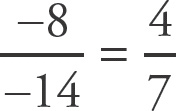
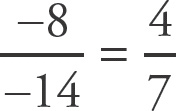 , and the value of Column B is
, and the value of Column B is 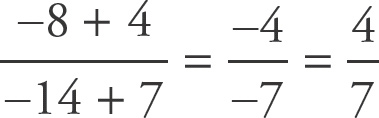
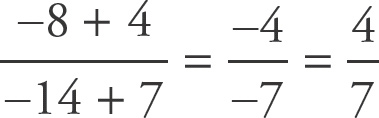 . If you are not convinced the values of the two columns will always be the same and have the time, you can try one more number set.
. If you are not convinced the values of the two columns will always be the same and have the time, you can try one more number set.
27. A

 You might start by setting up an equation, but you will see that it quickly becomes ugly: (x)(x + 1)(x + 2) = 504, so (x2 + x)(x + 2) = 504. So, try another approach, such as breaking 504 into its prime factors: 7 × 23 × 32. This means that the three numbers are 7, 8, and 9. As 7 > 6, choice (A) is correct.
You might start by setting up an equation, but you will see that it quickly becomes ugly: (x)(x + 1)(x + 2) = 504, so (x2 + x)(x + 2) = 504. So, try another approach, such as breaking 504 into its prime factors: 7 × 23 × 32. This means that the three numbers are 7, 8, and 9. As 7 > 6, choice (A) is correct.

 As there is an unknown value in one column and a known value in the other, test the known value against the unknown value. That is, assume that 6 is the least of the three numbers. The numbers would be 6, 7, and 8, with a product of 336. As 336 < 504, the least of the three numbers is greater than 6.
As there is an unknown value in one column and a known value in the other, test the known value against the unknown value. That is, assume that 6 is the least of the three numbers. The numbers would be 6, 7, and 8, with a product of 336. As 336 < 504, the least of the three numbers is greater than 6.
28. A

 As 89 is the mode, at a minimum there are two scores of 89. Let x, y, and z represent the three unknown scores, and set up the average formula:
As 89 is the mode, at a minimum there are two scores of 89. Let x, y, and z represent the three unknown scores, and set up the average formula: 
 = 88. Multiply both sides by 5 to find the sum of the five scores: x + y + z + 89 + 89 = 440. For Column A, let q represent the sixth score and set up another average formula:
= 88. Multiply both sides by 5 to find the sum of the five scores: x + y + z + 89 + 89 = 440. For Column A, let q represent the sixth score and set up another average formula: 
 = 89. Multiply both sides by 6 to find the sum of the six scores: q + x + y + z + 89 + 89 = 534. Subtract the sum of the five scores from the sum of the six scores to find q: 94. Now that you know Column A is 94, proceed to Column B. The median will be the average of the middle two scores. For the median to equal or exceed 94, the remaining three numbers would have to be listed to the right of 94, which means their sum would be greater than the sum of the known numbers. Check: 89 + 89 + 94 = 272, and x + y + z = 534 (the sum of the six) – 272: 262. Thus, 94 cannot be one of the middle numbers and is to the right of the middle numbers.
= 89. Multiply both sides by 6 to find the sum of the six scores: q + x + y + z + 89 + 89 = 534. Subtract the sum of the five scores from the sum of the six scores to find q: 94. Now that you know Column A is 94, proceed to Column B. The median will be the average of the middle two scores. For the median to equal or exceed 94, the remaining three numbers would have to be listed to the right of 94, which means their sum would be greater than the sum of the known numbers. Check: 89 + 89 + 94 = 272, and x + y + z = 534 (the sum of the six) – 272: 262. Thus, 94 cannot be one of the middle numbers and is to the right of the middle numbers.

 A good way to think of average is Total = Average × Number (TAN). Here, the number of tests is 5, and the current average is 88. Thus, the total score when all 5 tests are added is 440 (88 × 5). For Column A, find the total score for the six tests, using TAN: 6 × 89 = 534. Thus, to raise the average to 89, an additional score of 94 points is needed (534 – 440). For Column B, follow the procedure set forth immediately above.
A good way to think of average is Total = Average × Number (TAN). Here, the number of tests is 5, and the current average is 88. Thus, the total score when all 5 tests are added is 440 (88 × 5). For Column A, find the total score for the six tests, using TAN: 6 × 89 = 534. Thus, to raise the average to 89, an additional score of 94 points is needed (534 – 440). For Column B, follow the procedure set forth immediately above.
29. D

 Use logic. While it is possible that the reduction in area relates to the area of the base, it is equally possible that the height of Pyramid B is reduced by a factor of
Use logic. While it is possible that the reduction in area relates to the area of the base, it is equally possible that the height of Pyramid B is reduced by a factor of 
 while the area base is unchanged. (Other arrangements are possible as well.)
while the area base is unchanged. (Other arrangements are possible as well.)
30. A

 The sides of the square are 9, as all sides are equal. Thus, the area is 81. While the sides of the rectangle are unknown, try some possibilities to see how the different areas compare to 81. If the sides are 17 and 1, the area is 17. If the side are 10 and 8, the area is 80. There is no way to get the area up to 81 as long the rectangle is not a square.
The sides of the square are 9, as all sides are equal. Thus, the area is 81. While the sides of the rectangle are unknown, try some possibilities to see how the different areas compare to 81. If the sides are 17 and 1, the area is 17. If the side are 10 and 8, the area is 80. There is no way to get the area up to 81 as long the rectangle is not a square.

 A square of a given perimeter will always have the greatest possible area as compared to any rectangle with the same perimeter.
A square of a given perimeter will always have the greatest possible area as compared to any rectangle with the same perimeter.
31. C

 The area of the shaded region is the difference between the area of the large triangle and the area of the small triangle. The base of the large triangle is b, and its height is h, so the area of the triangle is
The area of the shaded region is the difference between the area of the large triangle and the area of the small triangle. The base of the large triangle is b, and its height is h, so the area of the triangle is 
 bh. The base of the small triangle is x, and its height is x, so the area of the triangle is
bh. The base of the small triangle is x, and its height is x, so the area of the triangle is 
 x2. Thus, the area of the shaded region is
x2. Thus, the area of the shaded region is 
 bh –
bh – 
 x2. Factor out the
x2. Factor out the 
 :
: 
 (bh – x2).
(bh – x2).

 Plug in values for b, h, and x, such as b = 10, h = 8, and x = 2. The area of the large triangle is
Plug in values for b, h, and x, such as b = 10, h = 8, and x = 2. The area of the large triangle is 
 × 10 × 8 = 40. The area of the small triangle is
× 10 × 8 = 40. The area of the small triangle is 
 × 2 × 2 = 2. The area of the shaded region is the difference between the two areas: 38. Substitute the selected values into the variables in Column B:
× 2 × 2 = 2. The area of the shaded region is the difference between the two areas: 38. Substitute the selected values into the variables in Column B: 
 (10 × 8 – 2) = 38.
(10 × 8 – 2) = 38.
32. C

 To compare the values in the two columns, you need to create a common base. As 27 = 33, the value in Column A is (33)4. When you raise a power to a power, multiply the exponents: 312.
To compare the values in the two columns, you need to create a common base. As 27 = 33, the value in Column A is (33)4. When you raise a power to a power, multiply the exponents: 312.
33. B

 In the figure, the x intercept is –2, and the y intercept is 3. When a line is reflected about the x axis, the x intercept stays the same, but the sign of the y intercept reverses. Thus, the value of Column A is –3. When a line is reflected about the y axis, the sign of the x intercept reverses, but the y intercept stays the same. Thus, the value of Column B is 3.
In the figure, the x intercept is –2, and the y intercept is 3. When a line is reflected about the x axis, the x intercept stays the same, but the sign of the y intercept reverses. Thus, the value of Column A is –3. When a line is reflected about the y axis, the sign of the x intercept reverses, but the y intercept stays the same. Thus, the value of Column B is 3.
34. A

 Consider different possible lengths given the area provided. If the rectangular garden were a square, the lengths would be 12 on all sides. The perimeter would be 48. If the rectangular garden had a length of 144 and width of 1, the perimeter would be 290. There is no way to create a perimeter of 44. Remember that a square of a certain area will always have a smaller perimeter than a rectangle of the same area.
Consider different possible lengths given the area provided. If the rectangular garden were a square, the lengths would be 12 on all sides. The perimeter would be 48. If the rectangular garden had a length of 144 and width of 1, the perimeter would be 290. There is no way to create a perimeter of 44. Remember that a square of a certain area will always have a smaller perimeter than a rectangle of the same area.
35. D

 Given that the absolute value of a and the absolute value of c are unknown, a + c can be any real number, including a number less than, equal to, or greater than b.
Given that the absolute value of a and the absolute value of c are unknown, a + c can be any real number, including a number less than, equal to, or greater than b.

 Plug in values for a, b, and c, following the restrictions, such as a = –2, b = 2, and c = 3. The value of Column A is 1, and the value of Column B is 2. As the value of Column A is not always greater than the value of Column B, and the values of the columns are not always equal, eliminate choices (A) and (C). Change up the numbers, trying to make the value of Column A greater if possible. Try c = 10, but keep a and b the same. Now, the value of Column A is 8, and the value of Column B is 2. As the value of Column B is not always greater than the value of Column A, eliminate choice (B) and select choice (D).
Plug in values for a, b, and c, following the restrictions, such as a = –2, b = 2, and c = 3. The value of Column A is 1, and the value of Column B is 2. As the value of Column A is not always greater than the value of Column B, and the values of the columns are not always equal, eliminate choices (A) and (C). Change up the numbers, trying to make the value of Column A greater if possible. Try c = 10, but keep a and b the same. Now, the value of Column A is 8, and the value of Column B is 2. As the value of Column B is not always greater than the value of Column A, eliminate choice (B) and select choice (D).
36. B

 The initial price of $2.50 fell after a 20% decrease to $2.00: 0.20 × $2.50 = $0.50, and $2.50 – $0.50 = $2.00. The new price of $2.00 went up after a 20% increase to $2.40: 0.20 × $2.00 = $0.40, and $2.00 + $0.40 = $2.40.
The initial price of $2.50 fell after a 20% decrease to $2.00: 0.20 × $2.50 = $0.50, and $2.50 – $0.50 = $2.00. The new price of $2.00 went up after a 20% increase to $2.40: 0.20 × $2.00 = $0.40, and $2.00 + $0.40 = $2.40.

 In this type of question, the original price does not matter, so plug in $100 to keep things simple. Subtracting 20% brings the price to $80. Adding 20% brings the price to $96. Thus decreasing a price by a percent and then increasing the price by the same percent will yield a price lower than the original amount.
In this type of question, the original price does not matter, so plug in $100 to keep things simple. Subtracting 20% brings the price to $80. Adding 20% brings the price to $96. Thus decreasing a price by a percent and then increasing the price by the same percent will yield a price lower than the original amount.
37. D

 Start with what you know and begin a list. The middle of five numbers is 4, and there are at least two 4s: _, _, 4, 4, _. (Note that the second 4 could be to the left of the median.) Given that the range (largest – smallest) is 4, there are a number of possibilities. Write one or two, just to get a sense of how things might look: 1, _, 4, 4, 5 & 2, _, 4, 4, 6. Now address Column B. A good way to think of mean is Total = Average × Number (TAN). Here, the number of numbers is 5, and the average is 4. Thus, the total of all five numbers when added is 20 (4 × 5). Put a number, such as 2, into the first list and find the average:
Start with what you know and begin a list. The middle of five numbers is 4, and there are at least two 4s: _, _, 4, 4, _. (Note that the second 4 could be to the left of the median.) Given that the range (largest – smallest) is 4, there are a number of possibilities. Write one or two, just to get a sense of how things might look: 1, _, 4, 4, 5 & 2, _, 4, 4, 6. Now address Column B. A good way to think of mean is Total = Average × Number (TAN). Here, the number of numbers is 5, and the average is 4. Thus, the total of all five numbers when added is 20 (4 × 5). Put a number, such as 2, into the first list and find the average: 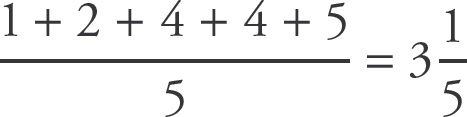
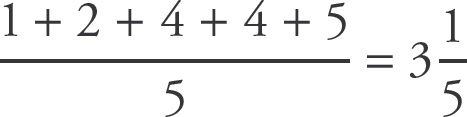 . As the value of Column A is not always greater than the value of Column B, and the values of the two columns are not always equal, eliminate choices (A) and (C). Now put a number, such as 4, into the second list and find the average:
. As the value of Column A is not always greater than the value of Column B, and the values of the two columns are not always equal, eliminate choices (A) and (C). Now put a number, such as 4, into the second list and find the average: 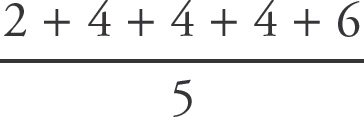
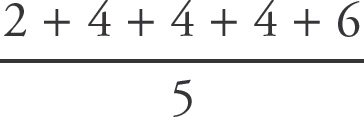 = 4. As the value of Column B is not always greater than the value of Column A, eliminate choice (B) and select choice (D).
= 4. As the value of Column B is not always greater than the value of Column A, eliminate choice (B) and select choice (D).
Section 3

 When you arrive at a new passage, read it quickly if you are a faster reader, or read the first sentence of each paragraph if you are a slower reader. For each detail question, read about 10 lines of text and try to predict what you believe will answer the question. Evaluate the answers against your prediction and make sure that the answer you selected is fully supported by the text.
When you arrive at a new passage, read it quickly if you are a faster reader, or read the first sentence of each paragraph if you are a slower reader. For each detail question, read about 10 lines of text and try to predict what you believe will answer the question. Evaluate the answers against your prediction and make sure that the answer you selected is fully supported by the text.
1. A

 The passage is narrated from the point of view of an adult recollecting his summers with family.
The passage is narrated from the point of view of an adult recollecting his summers with family.
2. D

 The passage states, “The owner of the restaurant was a callous man who yelled at the customers. I was quite frightened of him, but the hamburger with the special sauce was delicious, so I always wanted to go there for lunch.”
The passage states, “The owner of the restaurant was a callous man who yelled at the customers. I was quite frightened of him, but the hamburger with the special sauce was delicious, so I always wanted to go there for lunch.”
3. B

 The passage states, “I tried to teach my brother how to dive—he always jumped into the pool or even walked down the steps at the shallow end—but after a while I gave up.”
The passage states, “I tried to teach my brother how to dive—he always jumped into the pool or even walked down the steps at the shallow end—but after a while I gave up.”
4. B

 The passage states, “The owner of the restaurant was a callous man who yelled at the customers.”
The passage states, “The owner of the restaurant was a callous man who yelled at the customers.”
5. C

 The passage states, “Years later, I found out that my grandmother and her cousin liked going there for the hamburgers because they thought the owner’s rude behavior was funny!”
The passage states, “Years later, I found out that my grandmother and her cousin liked going there for the hamburgers because they thought the owner’s rude behavior was funny!”
6. B

 The passage states, “When I arrived, I was greeted by her little dog Charlie, whom I named. I loved Charlie, and we played for hours, chasing each other from room to room. Then, I would give Charlie a vanilla wafer as a treat.”
The passage states, “When I arrived, I was greeted by her little dog Charlie, whom I named. I loved Charlie, and we played for hours, chasing each other from room to room. Then, I would give Charlie a vanilla wafer as a treat.”
7. D

 The passage describes coral reefs generally and provides specific details about the Great Florida Reef.
The passage describes coral reefs generally and provides specific details about the Great Florida Reef.
8. A

 The passage states, “Given the scarcity of Atlantic and Caribbean reefs, it may come as a surprise that the second and third largest barrier reefs are the Belize Barrier Reef in Central America (620 miles), and the Great Florida Reef, a 4-mile wide, 145-mile long reef system that follows the arc of the Florida Keys.”
The passage states, “Given the scarcity of Atlantic and Caribbean reefs, it may come as a surprise that the second and third largest barrier reefs are the Belize Barrier Reef in Central America (620 miles), and the Great Florida Reef, a 4-mile wide, 145-mile long reef system that follows the arc of the Florida Keys.”
9. D

 Fish and other sea creatures would “visit” a reef.
Fish and other sea creatures would “visit” a reef.
10. B

 For choice (A), the passage states, “Farther out to sea are giant reefs that plunge into the deep.” For choice (C), the passage states, “The relatively shallow part of the Florida Straits (less than six feet deep) take on spur and groove formations—rows and rows of reefs separated by white sand.” For choice (D), the passage states, “In addition to fish similar to those in the patch reefs, the giant reefs are also frequented by large “pelagic” fish such as sharks.” There is no mention of lobsters and crustaceans in connect with the Florida Straits.
For choice (A), the passage states, “Farther out to sea are giant reefs that plunge into the deep.” For choice (C), the passage states, “The relatively shallow part of the Florida Straits (less than six feet deep) take on spur and groove formations—rows and rows of reefs separated by white sand.” For choice (D), the passage states, “In addition to fish similar to those in the patch reefs, the giant reefs are also frequented by large “pelagic” fish such as sharks.” There is no mention of lobsters and crustaceans in connect with the Florida Straits.
11. C

 This paragraph focuses on one specific part of the Great Florida Reef, rather than the Great Florida Reef generally.
This paragraph focuses on one specific part of the Great Florida Reef, rather than the Great Florida Reef generally.
12. C

 The author’s tone is positive.
The author’s tone is positive.
13. D

 The passage describes several women lawyers and their struggles to practice law.
The passage describes several women lawyers and their struggles to practice law.
14. C

 The passage states, “The Supreme Court agreed that she was a citizen, but rejected her argument that the “privileges and immunities” clause offered her protection. In a separate opinion for the Court, Joseph Bradley expressed the typical male view of the time.”
The passage states, “The Supreme Court agreed that she was a citizen, but rejected her argument that the “privileges and immunities” clause offered her protection. In a separate opinion for the Court, Joseph Bradley expressed the typical male view of the time.”
15. B

 For choice (A), the passage states, “When former United States Supreme Court Justice Sandra Day O’Connor graduated from Stanford Law School, the prestigious California law firms of the day would not hire her as a lawyer. Despite the fact that she graduated third in her class, the only job offer she received was as a legal secretary.” For choice (C), the passage states, “When former United States Supreme Court Justice Sandra Day O’Connor graduated from Stanford Law School, the prestigious California law firms of the day would not hire her as a lawyer. For choice (D), the passage states, “When former United States Supreme Court Justice Sandra Day O’Connor graduated from Stanford Law School, the prestigious California law firms of the day would not hire her as a lawyer.” Choice (B) is not supported; she was offered a job as a secretary, but the passage does not state that she accepted such a job.
For choice (A), the passage states, “When former United States Supreme Court Justice Sandra Day O’Connor graduated from Stanford Law School, the prestigious California law firms of the day would not hire her as a lawyer. Despite the fact that she graduated third in her class, the only job offer she received was as a legal secretary.” For choice (C), the passage states, “When former United States Supreme Court Justice Sandra Day O’Connor graduated from Stanford Law School, the prestigious California law firms of the day would not hire her as a lawyer. For choice (D), the passage states, “When former United States Supreme Court Justice Sandra Day O’Connor graduated from Stanford Law School, the prestigious California law firms of the day would not hire her as a lawyer.” Choice (B) is not supported; she was offered a job as a secretary, but the passage does not state that she accepted such a job.
16. D

 In discussing the Supreme Court opinion that denied a woman the right to be admitted to the bar, the author quotes Joseph Bradley’s reasoning as “the typical male view of the time.”
In discussing the Supreme Court opinion that denied a woman the right to be admitted to the bar, the author quotes Joseph Bradley’s reasoning as “the typical male view of the time.”
17. A

 The passage states, “Twenty years later, the Supreme Court similarly ruled against Belva Lockwood, who challenged Virginia’s refusal to admit her to the state Bar, even though she had been admitted to practice before the Supreme Court.”
The passage states, “Twenty years later, the Supreme Court similarly ruled against Belva Lockwood, who challenged Virginia’s refusal to admit her to the state Bar, even though she had been admitted to practice before the Supreme Court.”
18. C

 The passage states, “By the 1890s, though, admission of women to state Bars became increasingly common—even if prestigious law firms would not be ready to hire the likes of Justice O’Connor for decades to come.”
The passage states, “By the 1890s, though, admission of women to state Bars became increasingly common—even if prestigious law firms would not be ready to hire the likes of Justice O’Connor for decades to come.”
19. C

 The passage provides a description of the political writings of Liu Xiaobo and the Chinese government’s actions against him.
The passage provides a description of the political writings of Liu Xiaobo and the Chinese government’s actions against him.
20. D

 As the Chinese government arrested Liu Xiaobo, a word such as dislike (or villainy) is best.
As the Chinese government arrested Liu Xiaobo, a word such as dislike (or villainy) is best.
21. B

 In the third paragraph, the author provides an example of Liu’s political beliefs: “Liu has also been a staunch supporter of military action by the United States intended to expand human rights.” This example supports the author’s general discussion of Liu’s support of “fundamental human rights.”
In the third paragraph, the author provides an example of Liu’s political beliefs: “Liu has also been a staunch supporter of military action by the United States intended to expand human rights.” This example supports the author’s general discussion of Liu’s support of “fundamental human rights.”
22. B

 Liu Xiaobo was arrested for his political writings: “His crime: advocating political reforms in China, such as ending the Communist Party’s complete control of the political system and media.”
Liu Xiaobo was arrested for his political writings: “His crime: advocating political reforms in China, such as ending the Communist Party’s complete control of the political system and media.”
23. D

 The passage states, “Liu has also been a staunch supporter of military action by the United States intended to expand human rights: ‘The free world led by the US fought almost all regimes that trampled on human rights … The major wars that the US became involved in are all ethically defensible.’ He has also supported the United States’ support of Israel and the war in Iraq that led to Saddam Hussein’s downfall. He predicted that “a free, democratic and peaceful Iraq will emerge.”
The passage states, “Liu has also been a staunch supporter of military action by the United States intended to expand human rights: ‘The free world led by the US fought almost all regimes that trampled on human rights … The major wars that the US became involved in are all ethically defensible.’ He has also supported the United States’ support of Israel and the war in Iraq that led to Saddam Hussein’s downfall. He predicted that “a free, democratic and peaceful Iraq will emerge.”
24. C

 The passage states, “In his early years as an academic, his future role as dissident was not apparent. He spent many years studying literature, earning a Master’s Degree in 1984, when he was 29.”
The passage states, “In his early years as an academic, his future role as dissident was not apparent. He spent many years studying literature, earning a Master’s Degree in 1984, when he was 29.”
25. C

 The passage provides information about today’s understanding of the Black Death.
The passage provides information about today’s understanding of the Black Death.
26. A

 The passage states, “In France, the King was informed that the Plague was caused by astrological events such as the aligning of three planets.”
The passage states, “In France, the King was informed that the Plague was caused by astrological events such as the aligning of three planets.”
27. C

 The passage states, “But it is the Black Plague that continues to fascinate historians of disease, perhaps because after its first wave in the 1300s, it reappeared from time to time all the way through the 1700s.”
The passage states, “But it is the Black Plague that continues to fascinate historians of disease, perhaps because after its first wave in the 1300s, it reappeared from time to time all the way through the 1700s.”
28. B

 The plague ends swiftly after a population is destroyed.
The plague ends swiftly after a population is destroyed.
29. A

 The passage states, “Ultimately, this question, along with what caused the plague and how many people died, will never be answered conclusively. The records from the time are simply not detailed enough to allow for confident answers.”
The passage states, “Ultimately, this question, along with what caused the plague and how many people died, will never be answered conclusively. The records from the time are simply not detailed enough to allow for confident answers.”
30. C

 The passage states, “In addition to turning to astrology for answers, people of the time blamed earthquakes and, unfortunately, the Jewish people, whose communities in some towns were massacred not by the plague, but by other people.”
The passage states, “In addition to turning to astrology for answers, people of the time blamed earthquakes and, unfortunately, the Jewish people, whose communities in some towns were massacred not by the plague, but by other people.”
31. B

 The passage describes different types of igloos and how they are constructed to maintain warmth.
The passage describes different types of igloos and how they are constructed to maintain warmth.
32. B

 The passage states, “The bed is placed in a raised area, because warmer air rises.”
The passage states, “The bed is placed in a raised area, because warmer air rises.”
33. D

 Most of the passage describes the different designs and uses of igloos.
Most of the passage describes the different designs and uses of igloos.
34. B

 The passage states, “While the stone lamp may cause the interior to melt a bit, the water refreezes, which serves to strengthen the igloo.”
The passage states, “While the stone lamp may cause the interior to melt a bit, the water refreezes, which serves to strengthen the igloo.”
35. A

 The paragraph begins with a statement—that there are a number of different types of igloos. The rest of the paragraph provides examples.
The paragraph begins with a statement—that there are a number of different types of igloos. The rest of the paragraph provides examples.
36. A

 The passage states, “In the Inuit language, the word igloo means house, even though many people suppose it has a more precise definition: snow house. Quite the contrary, anything from a tent to a building can be called an igloo by the Inuit.”
The passage states, “In the Inuit language, the word igloo means house, even though many people suppose it has a more precise definition: snow house. Quite the contrary, anything from a tent to a building can be called an igloo by the Inuit.”
Section 4
1. D

 Choices (A) and (B) are the same as
Choices (A) and (B) are the same as 
 , as you can move the two decimals and reduce. Choice (C) is the decimal equivalent of
, as you can move the two decimals and reduce. Choice (C) is the decimal equivalent of 
 . Because
. Because 
 generates a repeating decimal in choice (D), choice (D) is not equivalent.
generates a repeating decimal in choice (D), choice (D) is not equivalent.

 Numbers divided by 3, 6, 7, and 9 generate repeating decimals. If you know this fact, you can select choice (D) without additional work.
Numbers divided by 3, 6, 7, and 9 generate repeating decimals. If you know this fact, you can select choice (D) without additional work.
2. B

 Find the radius by setting the given circumference equal to the formula for circumference: 12π = 2πr, so r = 6. Substitute the radius into the formula for area: π(62) = 36π.
Find the radius by setting the given circumference equal to the formula for circumference: 12π = 2πr, so r = 6. Substitute the radius into the formula for area: π(62) = 36π.
3. C

 A fraction will equal zero if the numerator equals zero. Here the numerator will equal zero if x2 = 36, as 36 – 36 = 0. There are two values of x that satisfy the equation: ±6.
A fraction will equal zero if the numerator equals zero. Here the numerator will equal zero if x2 = 36, as 36 – 36 = 0. There are two values of x that satisfy the equation: ±6.

 Test the answer choices. The numbers in choices (A) and (D) will not solve out to zero. While the number in choice (B) will, the answer is incomplete. Both numbers in choice (C) will solve out to zero.
Test the answer choices. The numbers in choices (A) and (D) will not solve out to zero. While the number in choice (B) will, the answer is incomplete. Both numbers in choice (C) will solve out to zero.
4. C

 First divide the coefficients:
First divide the coefficients: 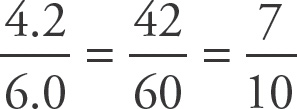
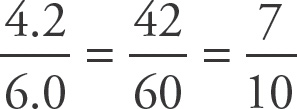 = 0.7. Next divide the exponential terms, remembering that when you divide common bases, you subtract the exponents:
= 0.7. Next divide the exponential terms, remembering that when you divide common bases, you subtract the exponents: 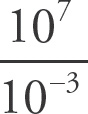
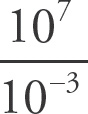 = 1010. As 0.7 × 1010 is not in proper scientific notation form, move the decimal forward once and decrease the exponent by one: 7.0 × 109.
= 1010. As 0.7 × 1010 is not in proper scientific notation form, move the decimal forward once and decrease the exponent by one: 7.0 × 109.
5. C

 There are 13 rectangles. As each is 4 in2, the total area is 13 × 4 in2 = 52 in2.
There are 13 rectangles. As each is 4 in2, the total area is 13 × 4 in2 = 52 in2.
6. C

 Begin with the coefficients. As the factors of 4 are 1, 2, and 4, and the factors of 10 are 1, 2, 5, 10, the greatest common factor is 2. As p5 is a factor of p8, the greatest common factor of p5 and p8 is p5. As q is a factor of q4, the greatest common factor of q and q4 is q.
Begin with the coefficients. As the factors of 4 are 1, 2, and 4, and the factors of 10 are 1, 2, 5, 10, the greatest common factor is 2. As p5 is a factor of p8, the greatest common factor of p5 and p8 is p5. As q is a factor of q4, the greatest common factor of q and q4 is q.
7. A

 Plug values from the chart into the answers. Begin with x = 1 and y = 0. Choices (A) and (B) both work, but choices (C) and (D) do not. Now test x = 2 and y = 2. Choice (A) still works, and choice (B) does not.
Plug values from the chart into the answers. Begin with x = 1 and y = 0. Choices (A) and (B) both work, but choices (C) and (D) do not. Now test x = 2 and y = 2. Choice (A) still works, and choice (B) does not.
8. B

 Use the slope formula:
Use the slope formula: 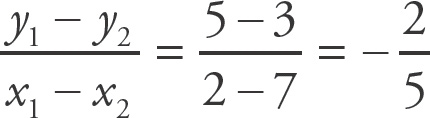
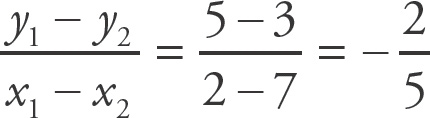 .
.
9. C

 List the numbers in order, being sure to use the y axis (miles): 1, 2, 4, 5, 6, 7, 7, 8. As there are an even number of numbers, the median is the average of the two middle numbers: 5.5.
List the numbers in order, being sure to use the y axis (miles): 1, 2, 4, 5, 6, 7, 7, 8. As there are an even number of numbers, the median is the average of the two middle numbers: 5.5.
10. A

 First add the terms inside the parentheses: x = 5x. For a number to equal five times that number, the number must be zero.
First add the terms inside the parentheses: x = 5x. For a number to equal five times that number, the number must be zero.

 Test the answer choices. Only choice (A) allows the equation to balance.
Test the answer choices. Only choice (A) allows the equation to balance.
11. C

 Use the distance formula for each answer:
Use the distance formula for each answer: 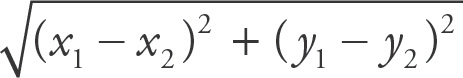
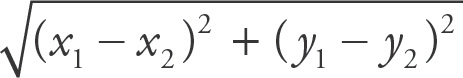 , which because one of the points is (0, 0) is
, which because one of the points is (0, 0) is 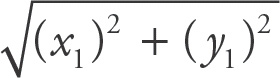
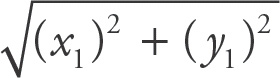 . Choice (A) yields 5, choice (B) yields
. Choice (A) yields 5, choice (B) yields 
 , choice (C) yields
, choice (C) yields 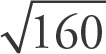
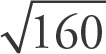 , and choice (D) yields 4
, and choice (D) yields 4 
 . As 13 =
. As 13 = 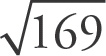
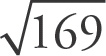 , choice (C) is closest.
, choice (C) is closest.

 Begin by estimating. Choices (A) and (D) are clearly too small. For the other two answers, draw in a line, creating a right triangle. While you can use the Pythagorean theorem, you may recall that one of the Pythagorean triples is 5-12-13. Therefore, the triangle with legs of 12 and 4 will have a hypotenuse closer to 13 than will the triangle with legs of 12 and 3.
Begin by estimating. Choices (A) and (D) are clearly too small. For the other two answers, draw in a line, creating a right triangle. While you can use the Pythagorean theorem, you may recall that one of the Pythagorean triples is 5-12-13. Therefore, the triangle with legs of 12 and 4 will have a hypotenuse closer to 13 than will the triangle with legs of 12 and 3.
12. B

 The smallest value of y is not necessarily determined by the smallest value of x, so try values of x on the ends and in the middle. If x = 2, then 3(2)2 – 4 = 8. If x = –3, then 3(–3)2 – 4 = 23. If x = 0, then 3(0)2 – 4 = –4. No value of x in the specified range will yield y = –7.
The smallest value of y is not necessarily determined by the smallest value of x, so try values of x on the ends and in the middle. If x = 2, then 3(2)2 – 4 = 8. If x = –3, then 3(–3)2 – 4 = 23. If x = 0, then 3(0)2 – 4 = –4. No value of x in the specified range will yield y = –7.
13. D

 Use the distance formula:
Use the distance formula: 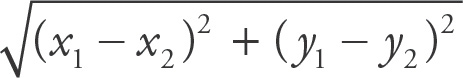
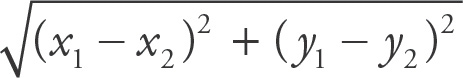 . Plugging in the given points yields
. Plugging in the given points yields 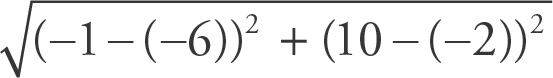
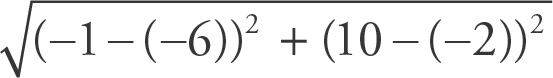 =
= 
 = 13.
= 13.

 Plot the points in the coordinate plane and connect them. This line is the hypotenuse of a right triangle, so drawn in the two legs. Count the number of units left to right and the number of units bottom to top. Use these numbers in the Pythagorean theorem.
Plot the points in the coordinate plane and connect them. This line is the hypotenuse of a right triangle, so drawn in the two legs. Count the number of units left to right and the number of units bottom to top. Use these numbers in the Pythagorean theorem.
14. A

 Pounds and tons measure weight, so eliminate choices (C) and (D). Choices (A) and (B) can be used to measure linear distance, but one kilometer is over 3,200 feet, much larger than a television screen.
Pounds and tons measure weight, so eliminate choices (C) and (D). Choices (A) and (B) can be used to measure linear distance, but one kilometer is over 3,200 feet, much larger than a television screen.
15. C

 When solving an equation with two inequality signs, perform the same operation to the two sides and the middle. Start by adding 1 to both sides and the middle: –3 ≤ 3x ≤ 9. Divide both sides by 3: –1 ≤ x ≤ 3.
When solving an equation with two inequality signs, perform the same operation to the two sides and the middle. Start by adding 1 to both sides and the middle: –3 ≤ 3x ≤ 9. Divide both sides by 3: –1 ≤ x ≤ 3.
16. A

 The mode is the number that appears the most. Be sure to focus on the number of times a certain number of inches of rain fell. Two inches of rain fell 12 times, so 2 is the mode.
The mode is the number that appears the most. Be sure to focus on the number of times a certain number of inches of rain fell. Two inches of rain fell 12 times, so 2 is the mode.
17. C

 The number of arrangements possible when r are selected from n options is given by
The number of arrangements possible when r are selected from n options is given by 
 . Here, the number of arrangements is
. Here, the number of arrangements is 
 = 7 × 6 × 5 = 210.
= 7 × 6 × 5 = 210.

 When dealing with orderings or combinations, you can set up slots for what you need and fill them with what is available. In this case we need three people, so we need three slots: ___ ___ ___ . For the first slot, 7 people are available as a possible choice, while for the second slot only 6 people are available (as one is taken for the first slot), and for the third slot only 5 people are available (as another was taken away): 7 6 5 . To find the number of arrangements, multiply the numbers in the slots: 210.
When dealing with orderings or combinations, you can set up slots for what you need and fill them with what is available. In this case we need three people, so we need three slots: ___ ___ ___ . For the first slot, 7 people are available as a possible choice, while for the second slot only 6 people are available (as one is taken for the first slot), and for the third slot only 5 people are available (as another was taken away): 7 6 5 . To find the number of arrangements, multiply the numbers in the slots: 210.
18. A

 Questions seeking the area of a weird shaded region generally require you to subtract the area of one normal shape from the area of another normal shape. In this case, subtract the area of the triangle from the area of the quarter circle. The area of a quarter circle is
Questions seeking the area of a weird shaded region generally require you to subtract the area of one normal shape from the area of another normal shape. In this case, subtract the area of the triangle from the area of the quarter circle. The area of a quarter circle is 
 πr2 =
πr2 = 
 π(6)2 = 9π. As the triangle is a right triangle, the radii are also the base and height. The area of a triangle is
π(6)2 = 9π. As the triangle is a right triangle, the radii are also the base and height. The area of a triangle is 
 bh =
bh = 
 (6)(6) = 18. Choice (A) reflects the difference between the two areas.
(6)(6) = 18. Choice (A) reflects the difference between the two areas.

 You can estimate that the area is a small fraction of the area of the circle, which is 36π or approximately 108. Choices (B) and (C) are negative, so you can eliminate them. Choice (A) is about 9, while choice (D) is about 72. Given that one quarter of the circle is about 72, choice (D) is too large.
You can estimate that the area is a small fraction of the area of the circle, which is 36π or approximately 108. Choices (B) and (C) are negative, so you can eliminate them. Choice (A) is about 9, while choice (D) is about 72. Given that one quarter of the circle is about 72, choice (D) is too large.
19. B

 Percent change is calculated as follows:
Percent change is calculated as follows: 
 , so the number of students increased by 25%:
, so the number of students increased by 25%: 
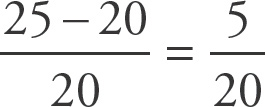 × 100 = 25%.
× 100 = 25%.
20. C

 A rational number can be expressed as a fraction. The square root of a number that is not a perfect square is irrational. The expression in choice (C) can be rational because squaring the square root of a number yields that number. Thus both x2 and y2 will be rational, so the quotient of those numbers will be rational.
A rational number can be expressed as a fraction. The square root of a number that is not a perfect square is irrational. The expression in choice (C) can be rational because squaring the square root of a number yields that number. Thus both x2 and y2 will be rational, so the quotient of those numbers will be rational.

 Plug in values for x and y following the restriction, such as x =
Plug in values for x and y following the restriction, such as x = 
 and y =
and y = 
 . These numbers are both irrational, as they cannot be expressed as a fraction. Substitute these numbers into each answer choices to determine when the expression can be expressed as a fraction. Only choice (C) can.
. These numbers are both irrational, as they cannot be expressed as a fraction. Substitute these numbers into each answer choices to determine when the expression can be expressed as a fraction. Only choice (C) can.
21. A

 Draw the triangles to make sure the corresponding vertices of the two triangles are aligned. Set up a proportion:
Draw the triangles to make sure the corresponding vertices of the two triangles are aligned. Set up a proportion: 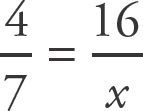
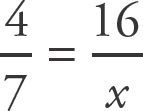 . Cross multiply and divide both sides by 4.
. Cross multiply and divide both sides by 4.
22. C

 Use FOIL (First, Outside, Inside, Last) on the two factors: (x + 4)(x – 5) = (x2 + 4x– 5x – 20). Combine like terms: x2 – x – 20.
Use FOIL (First, Outside, Inside, Last) on the two factors: (x + 4)(x – 5) = (x2 + 4x– 5x – 20). Combine like terms: x2 – x – 20.

 Plug in a number for x, such as x = 6, and solve: (6 + 4)(6 – 5) = (10)(1) = 10. Only choice (C) yields 10 when the value for x is plugged in.
Plug in a number for x, such as x = 6, and solve: (6 + 4)(6 – 5) = (10)(1) = 10. Only choice (C) yields 10 when the value for x is plugged in.
23. B

 There are 360 degrees in a quadrilateral. Add up the given angles and subtract the sum from 360: 360 – (140 + 80 + 25) = 360 – 245 = 115.
There are 360 degrees in a quadrilateral. Add up the given angles and subtract the sum from 360: 360 – (140 + 80 + 25) = 360 – 245 = 115.
24. A

 First, multiply both sides by (4 + x): x(4 + x) = –4. Distribute the x: 4x + x2 = –4. Add 4 to both sides and order the left side by leading exponent: x2 + 4x + 4 = 0. Factor the left side of the equation: (x + 2)(x + 2) = 0. Set x + 2 equal to 0 and subtract 2 from both sides: x = –2.
First, multiply both sides by (4 + x): x(4 + x) = –4. Distribute the x: 4x + x2 = –4. Add 4 to both sides and order the left side by leading exponent: x2 + 4x + 4 = 0. Factor the left side of the equation: (x + 2)(x + 2) = 0. Set x + 2 equal to 0 and subtract 2 from both sides: x = –2.

 Test the answers. The value in choice (A) allows the equation to balance, so eliminate choices (B) and (D). Test any other number, and the equation will not balance. Eliminate choice (C).
Test the answers. The value in choice (A) allows the equation to balance, so eliminate choices (B) and (D). Test any other number, and the equation will not balance. Eliminate choice (C).
25. D

 First, distribute the negative sign: 3a3b5 + 2a2b4 – 7a2b4 + 4a3b5. Carefully combine like terms: 7a3b5 – 5a2b4.
First, distribute the negative sign: 3a3b5 + 2a2b4 – 7a2b4 + 4a3b5. Carefully combine like terms: 7a3b5 – 5a2b4.
26. D

 As the square of an odd number is odd, and the difference between two odd numbers is even, choice (D) will yield an even number when x is odd.
As the square of an odd number is odd, and the difference between two odd numbers is even, choice (D) will yield an even number when x is odd.

 Plug an odd value for x, such as x = 3, into the answer choices. Only choice (D) is even.
Plug an odd value for x, such as x = 3, into the answer choices. Only choice (D) is even.
27. B

 This question is testing the relationship between similar triangles. Set up a proportion:
This question is testing the relationship between similar triangles. Set up a proportion: 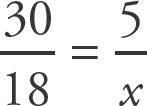
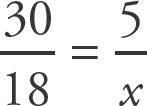 . Cross multiply and divide both sides by 30.
. Cross multiply and divide both sides by 30.
28. B

 First take the square root of 64: 8. For the variable, you must use the rules of exponents. If the bases are the same, add the exponents when you multiply the terms. The term x36 represents a base of x that was squared, i.e., multiplied by itself. Thus the two exponents added were the same value and produced a sum of 36. (x18)(x18) = x36.
First take the square root of 64: 8. For the variable, you must use the rules of exponents. If the bases are the same, add the exponents when you multiply the terms. The term x36 represents a base of x that was squared, i.e., multiplied by itself. Thus the two exponents added were the same value and produced a sum of 36. (x18)(x18) = x36.

 To find the square root, divide the exponent in half.
To find the square root, divide the exponent in half. 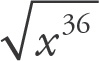
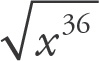 = x18.
= x18.
29. D

 The 60 people who chose Comedy represent
The 60 people who chose Comedy represent 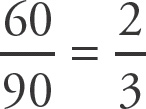
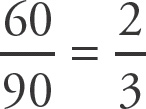 of the survey participants. To represent this fraction in a circle graph, which has 360°, set up a proportion:
of the survey participants. To represent this fraction in a circle graph, which has 360°, set up a proportion: 
 . Cross multiply and divide by 3.
. Cross multiply and divide by 3.
30. C

 Probability is always a fraction,
Probability is always a fraction, 
 . In the first reach into the bag of beads, we want a yellow bead (9) out of all the beads (16). Therefore, the first reach is
. In the first reach into the bag of beads, we want a yellow bead (9) out of all the beads (16). Therefore, the first reach is 
 . For the second reach, we want a purple bead (2), but there is one less bead total, so the probability of getting a purple bead is
. For the second reach, we want a purple bead (2), but there is one less bead total, so the probability of getting a purple bead is 
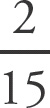 . When you need two probabilities to occur, you multiply the fractions.
. When you need two probabilities to occur, you multiply the fractions.
31. C

 As 36 + 9 = 45, and
As 36 + 9 = 45, and 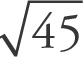
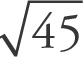 is not an integer, choice (C) is correct.
is not an integer, choice (C) is correct.
32. A

 The slope of a line perpendicular to another line is the negative reciprocal of the other line’s slope. The negative reciprocal of
The slope of a line perpendicular to another line is the negative reciprocal of the other line’s slope. The negative reciprocal of 
 is −
is −
 .
.
33. C

 First, determine how much time was devoted to changing scenery by dividing 80 minutes by 5: 16 minutes. Next, convert 16 minutes to seconds, so you have an apples-to-apples comparison, by multiplying 16 by 60: 960. Finally divide 960 by 40: 24.
First, determine how much time was devoted to changing scenery by dividing 80 minutes by 5: 16 minutes. Next, convert 16 minutes to seconds, so you have an apples-to-apples comparison, by multiplying 16 by 60: 960. Finally divide 960 by 40: 24.
34. C

 Test the answers to determine which one yields the indicated graph. For each answer, there are two cases. For choice (A), first solve x + 4 ≤ 6. Subtract 4 from both sides: x ≤ 2. As this is not one of the indicated end points in the graph, eliminate choice (A). For choice (B), first solve x + 4 ≤ –6. Subtract 4 from both sides: x ≤ –10. As this is not one of the indicated end points in the graph, eliminate choice (B). For choice (C), first solve x – 4 ≤ 6. Add 4 to both sides: x ≤ 10. This is consistent with the graph. Now, solve x – 4 ≥ –6. Add 4 to both sides: x ≥ –2. This is also consistent with the graph, so choice (C) is correct.
Test the answers to determine which one yields the indicated graph. For each answer, there are two cases. For choice (A), first solve x + 4 ≤ 6. Subtract 4 from both sides: x ≤ 2. As this is not one of the indicated end points in the graph, eliminate choice (A). For choice (B), first solve x + 4 ≤ –6. Subtract 4 from both sides: x ≤ –10. As this is not one of the indicated end points in the graph, eliminate choice (B). For choice (C), first solve x – 4 ≤ 6. Add 4 to both sides: x ≤ 10. This is consistent with the graph. Now, solve x – 4 ≥ –6. Add 4 to both sides: x ≥ –2. This is also consistent with the graph, so choice (C) is correct.
35. B

 First, convert the length and width from feet to yards by dividing each number by 3: the measurements are 5 yards and 7 yards. Find the area: 35 yd2. As each tile has an area of 1 yd2, 35 tiles will be needed.
First, convert the length and width from feet to yards by dividing each number by 3: the measurements are 5 yards and 7 yards. Find the area: 35 yd2. As each tile has an area of 1 yd2, 35 tiles will be needed.
36. D

 First subtract 25 from both sides: x2 = –25. Take the square root of each side, remembering the there are two solutions for x2: x =
First subtract 25 from both sides: x2 = –25. Take the square root of each side, remembering the there are two solutions for x2: x = 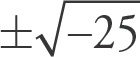
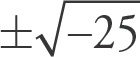 . Separate the 25 from –1:
. Separate the 25 from –1: 
 . The square root of negative one is not a real number and is called the imaginary number i. Thus, x = ±5i.
. The square root of negative one is not a real number and is called the imaginary number i. Thus, x = ±5i.
37. B

 To add matrices, add the numbers that occupy the same position in each matrix. That is, add the top-left numbers, the top-right numbers, and so on. Here,
To add matrices, add the numbers that occupy the same position in each matrix. That is, add the top-left numbers, the top-right numbers, and so on. Here, 
 =
= 
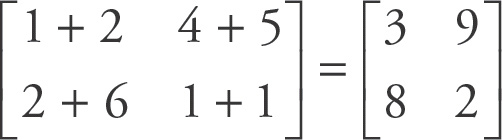 .
.
38. A

 First, add a to both sides and subtract ab from both sides: a + 3 = xb – ab. Factor out b from the right side: a + 3 = b(x – a). Divide both sides by x – a:
First, add a to both sides and subtract ab from both sides: a + 3 = xb – ab. Factor out b from the right side: a + 3 = b(x – a). Divide both sides by x – a: 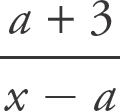
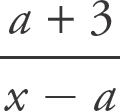 = b.
= b.

 Plug in values for two of the variables, such as a = 6 and b = 4, and solve for x: (6)(4) + 3 = 3x – 6, so 24 = 3x – 6, so 3x + 30, so x = 10. Test the values for x and a in the answers to find the value for b. Only choice (A) works.
Plug in values for two of the variables, such as a = 6 and b = 4, and solve for x: (6)(4) + 3 = 3x – 6, so 24 = 3x – 6, so 3x + 30, so x = 10. Test the values for x and a in the answers to find the value for b. Only choice (A) works.
39. D

 A stem-and-leaf plot shows the tens digit to the left of the vertical line and the units digits to the right of the vertical line. Thus, in the second row, the first number is 11, and the next is 14. Because all of the numbers of the data set are given, all statistical measures (mean, median, mode, and range) can be assessed.
A stem-and-leaf plot shows the tens digit to the left of the vertical line and the units digits to the right of the vertical line. Thus, in the second row, the first number is 11, and the next is 14. Because all of the numbers of the data set are given, all statistical measures (mean, median, mode, and range) can be assessed.
40. B

 Let x represent the smaller number and set up an equation: x + x + 8 = 26. Combine like terms and subtract 8 from both sides: 2x = 18. Divide both sides by 2: x = 9.
Let x represent the smaller number and set up an equation: x + x + 8 = 26. Combine like terms and subtract 8 from both sides: 2x = 18. Divide both sides by 2: x = 9.

 Test the answers, starting with choice (B) or (C). If you start with choice (C), the smaller piece is 17, so the larger piece is 25. The sum of these pieces is 42, which is too large. Proceed to choice (B). If the smaller piece is 9, the larger piece is 17. The sum is 26.
Test the answers, starting with choice (B) or (C). If you start with choice (C), the smaller piece is 17, so the larger piece is 25. The sum of these pieces is 42, which is too large. Proceed to choice (B). If the smaller piece is 9, the larger piece is 17. The sum is 26.
41. C

 To find the area of an irregularly shaped shaded region, find the areas of the two normal shapes and subtract the smaller from the larger. As the area of a circle is πr2, the area of the larger circle is 100π, and the area of the smaller circle is 36π. The difference is 64π.
To find the area of an irregularly shaped shaded region, find the areas of the two normal shapes and subtract the smaller from the larger. As the area of a circle is πr2, the area of the larger circle is 100π, and the area of the smaller circle is 36π. The difference is 64π.

 You can estimate that the area is a fraction of the area of the larger circle (100π = approximately 300, as π is approximately 3). Estimate the values of the answer choices. Choice (A) is 48, which is too small. Choice (B) is 108, which might work. Choice (C) is 192, which might work. Choice (D) is the area of the larger circle, which is too big. While it may be difficult to determine whether the shaded region is about
You can estimate that the area is a fraction of the area of the larger circle (100π = approximately 300, as π is approximately 3). Estimate the values of the answer choices. Choice (A) is 48, which is too small. Choice (B) is 108, which might work. Choice (C) is 192, which might work. Choice (D) is the area of the larger circle, which is too big. While it may be difficult to determine whether the shaded region is about 
 or
or 
 of the larger circle, consider that farther out from the center takes up more area than closer to the center. Thus, choice (C) may be a safer bet.
of the larger circle, consider that farther out from the center takes up more area than closer to the center. Thus, choice (C) may be a safer bet.
42. B

 The vertical lines at either end of the box-and-whisker graph represent the lowest and highest data points. (The vertical line in the middle of the two boxes represents the median.) As range is calculated by subtracting the lowest value from the highest value, the range here is 70 – 25 = 45.
The vertical lines at either end of the box-and-whisker graph represent the lowest and highest data points. (The vertical line in the middle of the two boxes represents the median.) As range is calculated by subtracting the lowest value from the highest value, the range here is 70 – 25 = 45.
43. D

 Begin by stating the speed as a fraction with the units marked:
Begin by stating the speed as a fraction with the units marked: 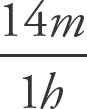
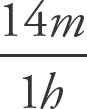 . Now, convert the miles in to feet. As there are 5,280 feet in a mile, multiply 14 in the numerator by 5,280:
. Now, convert the miles in to feet. As there are 5,280 feet in a mile, multiply 14 in the numerator by 5,280: 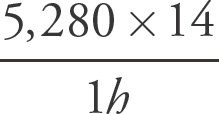
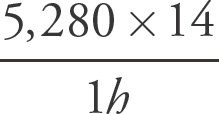 . Now, convert the hour into minutes. As there are 60 minutes per hour, multiply the 1 in the denominator by 60:
. Now, convert the hour into minutes. As there are 60 minutes per hour, multiply the 1 in the denominator by 60: 
 .
.
44. D

 Probability is always a fraction,
Probability is always a fraction, 
 . The total number of jelly beans to begin with is 19, but Graciela removes a brown one, leaving 18 jelly beans behind, 5 of which are pink. Graciela’s probability of removing a pink one is therefore
. The total number of jelly beans to begin with is 19, but Graciela removes a brown one, leaving 18 jelly beans behind, 5 of which are pink. Graciela’s probability of removing a pink one is therefore 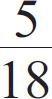
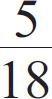 .
.
45. A

 Use SohCahToa. As
Use SohCahToa. As 
 is OPPOSITE TO the given angle, and
is OPPOSITE TO the given angle, and 
 is ADJACENT TO the given angle, use tangent: tan 50° =
is ADJACENT TO the given angle, use tangent: tan 50° = 
 . Multiply both sides by 5: 5 tan 50° =
. Multiply both sides by 5: 5 tan 50° = 
 .
.
46. A

 As the diameter is 4, the radius is 2. The height—three times the radius—is 6. Substitute these numbers into the given formula:
As the diameter is 4, the radius is 2. The height—three times the radius—is 6. Substitute these numbers into the given formula: 
 π(22)(6) =
π(22)(6) = 
 π(4)(6) = 8π.
π(4)(6) = 8π.
47. C

 To determine whether a specified value is within a given range around a middle or normal value, subtract the middle value from the specific value, take the absolute value of that difference, and determine whether the result is less than or equal to the given range. That is |specific – middle| ≤ range. In this case, R is the specified value, 20 is the middle value, and 5 is the given range, so |R – 20| ≤ 5.
To determine whether a specified value is within a given range around a middle or normal value, subtract the middle value from the specific value, take the absolute value of that difference, and determine whether the result is less than or equal to the given range. That is |specific – middle| ≤ range. In this case, R is the specified value, 20 is the middle value, and 5 is the given range, so |R – 20| ≤ 5.

 Plug in a permitted value for R, such as 22. Test 22 in each answer. For choice (A), |22 – 5| ≤ 20. This is true, so keep choice (A). For choice (B), |22 – 5| ≥ 20. This is false, so eliminate choice (B). For choice (C), |22 – 20| ≤ 5. This is true, so keep choice (C). For choice (D), |22 – 20| ≥ 5. This is false, so eliminate choice (D). As two answers remain, try a value for R that is not permitted, such as 13. In this case, the equation should fail, as 13 is not permitted. For choice (A), |13 – 5| ≤ 20. This is true, so eliminate choice (A). For choice (C), |13 – 20| ≤ 5. This is false, so keep choice (C).
Plug in a permitted value for R, such as 22. Test 22 in each answer. For choice (A), |22 – 5| ≤ 20. This is true, so keep choice (A). For choice (B), |22 – 5| ≥ 20. This is false, so eliminate choice (B). For choice (C), |22 – 20| ≤ 5. This is true, so keep choice (C). For choice (D), |22 – 20| ≥ 5. This is false, so eliminate choice (D). As two answers remain, try a value for R that is not permitted, such as 13. In this case, the equation should fail, as 13 is not permitted. For choice (A), |13 – 5| ≤ 20. This is true, so eliminate choice (A). For choice (C), |13 – 20| ≤ 5. This is false, so keep choice (C).
Writing Sample
Give your essay to a parent or teacher, along with the prompt. Your reviewer should comment on whether someone working in an admissions office would think that you are nice, thoughtful, funny, or any other positive quality. Your reviewer should also focus on organization, grammar, spelling, and other aspects of good writing, but he or she should not hold you to the standard required of a well-polished essay. While glaring problems should be identified, very few people will write a perfect first draft in a timed setting.

 To liberate is to free something.
To liberate is to free something.
 Tangible means touchable or concrete.
Tangible means touchable or concrete.
 Innate means inborn or native.
Innate means inborn or native.
 To deliberate is to consider or reflect.
To deliberate is to consider or reflect.
 Pious means virtuous or sacred.
Pious means virtuous or sacred.
 To plea is to request.
To plea is to request.
 The word please shares the same root.
The word please shares the same root.
 To disperse is to scatter.
To disperse is to scatter.
 Renown means fame.
Renown means fame.
 To venerate is to respect.
To venerate is to respect.
 To plunder is to steal.
To plunder is to steal.
 Voracious means having a huge appetite or gluttonous.
Voracious means having a huge appetite or gluttonous.
 Belligerent means argumentative.
Belligerent means argumentative.
 The Latin root bell means war. The period before the Civil War is called the ante-bellum period. The word rebel comes from the same root.
The Latin root bell means war. The period before the Civil War is called the ante-bellum period. The word rebel comes from the same root.
 Ominous means worrisome.
Ominous means worrisome.
 Zealous means passionate.
Zealous means passionate.
 A benediction is a blessing.
A benediction is a blessing.
 The Latin root bene means good, and the root dict means word, so a benediction is a good word, a blessing.
The Latin root bene means good, and the root dict means word, so a benediction is a good word, a blessing.
 Disparate means unequal.
Disparate means unequal.
 The Latin root dis means not, and the root par means equal.
The Latin root dis means not, and the root par means equal.
 Aggrandize means exaggerate.
Aggrandize means exaggerate.
 To distinguish is to separate or differentiate.
To distinguish is to separate or differentiate.
 Equivocal means ambiguous.
Equivocal means ambiguous.
 The Latin root equ means equal, and the root voc means voice, so equivocal means equal voiced, which is to say ambiguous in meaning.
The Latin root equ means equal, and the root voc means voice, so equivocal means equal voiced, which is to say ambiguous in meaning.
 A malcontent is a grouch.
A malcontent is a grouch.
 The Latin root mal means bad.
The Latin root mal means bad.
 Utter sorrow requires anguish (suffering) as the answer.
Utter sorrow requires anguish (suffering) as the answer.
 Even if you do not know the word anguish, you can eliminate the other answers because the correct answer must mean utter sorrow.
Even if you do not know the word anguish, you can eliminate the other answers because the correct answer must mean utter sorrow.
 Years of practice and lacks the tremendous talent requires adept (able) as the answer.
Years of practice and lacks the tremendous talent requires adept (able) as the answer.
 Even if you do not know the word adept, you can eliminate the other answers because the correct answer must reflect the result of years of lessons yet without tremendous talent.
Even if you do not know the word adept, you can eliminate the other answers because the correct answer must reflect the result of years of lessons yet without tremendous talent.
 Did not realize I was making an accusation requires insinuate (hint) as the answer.
Did not realize I was making an accusation requires insinuate (hint) as the answer.
 Even if you do not know the word insinuate, you can eliminate the other answers because the correct answer must reflect that the speaker made an accusation that the listener did not realize was an accusation.
Even if you do not know the word insinuate, you can eliminate the other answers because the correct answer must reflect that the speaker made an accusation that the listener did not realize was an accusation.
 Showered his friends with gifts and gave his time requires generous as the answer.
Showered his friends with gifts and gave his time requires generous as the answer.
 Enthusiasm and positive attitude never require diminished.
Enthusiasm and positive attitude never require diminished.
 False doctrine and injustice require ignoble (shameful) as the answer.
False doctrine and injustice require ignoble (shameful) as the answer.
 Even if you do not know the word ignoble, you can eliminate choices (A) and (C), as well as choice (D) if you know the word, because the correct answer must reflect false doctrine and injustice.
Even if you do not know the word ignoble, you can eliminate choices (A) and (C), as well as choice (D) if you know the word, because the correct answer must reflect false doctrine and injustice.
 Naive and unlikely, believe, and true require ruse (trick) as the answer.
Naive and unlikely, believe, and true require ruse (trick) as the answer.
 Even if you do not know the word ruse, you can eliminate choices (A) and (C), as well as choice (B) if you know it, because the correct answer must reflect that Matthew is naive and will believe unlikely things are true.
Even if you do not know the word ruse, you can eliminate choices (A) and (C), as well as choice (B) if you know it, because the correct answer must reflect that Matthew is naive and will believe unlikely things are true.
 Could not be resolved requires impasse (stalemate or deadlock) as the answer.
Could not be resolved requires impasse (stalemate or deadlock) as the answer.
 Even if you do not know the word impasse, you can eliminate choices (B) and (D), as well as choice (A) if you know it, because the correct answer must reflect that an issue could not be resolved.
Even if you do not know the word impasse, you can eliminate choices (B) and (D), as well as choice (A) if you know it, because the correct answer must reflect that an issue could not be resolved.
 Always in high spirits requires jubilant (joyous) as the answer.
Always in high spirits requires jubilant (joyous) as the answer.
 Even if you do not know the word jubilant, you can eliminate choice (A), as well as choices (C) and (D) if you know them, because the correct answer must reflect always in high spirits. You may need to guess from three choices.
Even if you do not know the word jubilant, you can eliminate choice (A), as well as choices (C) and (D) if you know them, because the correct answer must reflect always in high spirits. You may need to guess from three choices.
 Activities of dancers requires kinetic (relating to motion) as the answer.
Activities of dancers requires kinetic (relating to motion) as the answer.
 Even if you do not know the word kinetic, you can eliminate the other answers because the correct answer must reflect activity of dancers.
Even if you do not know the word kinetic, you can eliminate the other answers because the correct answer must reflect activity of dancers.
 Both blanks must relate to could speak powerfully and expressively, thus requiring eloquence (well spoken) and verbalize as the answer.
Both blanks must relate to could speak powerfully and expressively, thus requiring eloquence (well spoken) and verbalize as the answer.
 Do one blank at a time. The first blank, which might seem easier, must reflect that the sister could speak powerfully and expressively, so you can eliminate choices (A), (B), and (D). The second blank must also relate to could speak powerfully and expressively. The Latin root loc/loq means speech.
Do one blank at a time. The first blank, which might seem easier, must reflect that the sister could speak powerfully and expressively, so you can eliminate choices (A), (B), and (D). The second blank must also relate to could speak powerfully and expressively. The Latin root loc/loq means speech.
 The first blank must mean believe, while the second blank must mean praises, thus requiring suppose and extol (praise) as the answer.
The first blank must mean believe, while the second blank must mean praises, thus requiring suppose and extol (praise) as the answer.
 Do one blank at a time. The second blank, which might seem easier, must mean praise, so you can eliminate choices (A), (B), and (C). The first blank must mean believe.
Do one blank at a time. The second blank, which might seem easier, must mean praise, so you can eliminate choices (A), (B), and (C). The first blank must mean believe.
 The first blank must mean bad, while the second blank must mean confirmed, thus requiring maladroit (clumsy or unskilled) and perpetuated (continued) as the answer.
The first blank must mean bad, while the second blank must mean confirmed, thus requiring maladroit (clumsy or unskilled) and perpetuated (continued) as the answer.
 Do one blank at a time. The first blank, which might seem easier, must reflect unable to do anything, so you can eliminate choices (B) and (C). The first blank must mean confirmed, so you can eliminate choice (A). The Latin root mal means bad, and adroit means skilled.
Do one blank at a time. The first blank, which might seem easier, must reflect unable to do anything, so you can eliminate choices (B) and (C). The first blank must mean confirmed, so you can eliminate choice (A). The Latin root mal means bad, and adroit means skilled.
 The first blank must be the opposite of nasty, while the second blank must reflect how the parents reacted to bad news, thus requiring benign (kindness) and chagrin (irritation) as the answer.
The first blank must be the opposite of nasty, while the second blank must reflect how the parents reacted to bad news, thus requiring benign (kindness) and chagrin (irritation) as the answer.
 Do one blank at a time. The first blank, which might seem easier, must be the opposite of nasty, so you can eliminate choice (B), as well as choice (D) if you know it. The second blank must reflect how the parents reacted to bad news, so you can eliminate choice (C). You may need to guess between choices (A) and (C). The Latin root ben means good.
Do one blank at a time. The first blank, which might seem easier, must be the opposite of nasty, so you can eliminate choice (B), as well as choice (D) if you know it. The second blank must reflect how the parents reacted to bad news, so you can eliminate choice (C). You may need to guess between choices (A) and (C). The Latin root ben means good.
 The first blank must be the opposite of lack of brevity, while the second blank must reflect an unsatisfied hope, thus requiring concisely (briefly) and undermining (weakening) as the answer.
The first blank must be the opposite of lack of brevity, while the second blank must reflect an unsatisfied hope, thus requiring concisely (briefly) and undermining (weakening) as the answer.
 Do one blank at a time. The first blank, which might seem easier if you know the word brevity (briefness), must be the opposite of brevity, so you can eliminate choices (A) and (C). If you don’t know brevity, you cannot eliminate any first-blank answers. The second blank must reflect an unsatisfied hope, so you can eliminate choice (D), as well as choice (A) if you haven’t eliminated it already. You may need to guess between choices (B) and (C).
Do one blank at a time. The first blank, which might seem easier if you know the word brevity (briefness), must be the opposite of brevity, so you can eliminate choices (A) and (C). If you don’t know brevity, you cannot eliminate any first-blank answers. The second blank must reflect an unsatisfied hope, so you can eliminate choice (D), as well as choice (A) if you haven’t eliminated it already. You may need to guess between choices (B) and (C).
 The first blank must mean hurtful, while the second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, thus requiring malicious (hateful) and ameliorate (improve) as the answer.
The first blank must mean hurtful, while the second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, thus requiring malicious (hateful) and ameliorate (improve) as the answer.
 Do one blank at a time. The first blank, which might seem easier, must mean hurtful, so you can eliminate choices (A) and (B). The second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, so you can eliminate choice (D). The Latin root mal means bad.
Do one blank at a time. The first blank, which might seem easier, must mean hurtful, so you can eliminate choices (A) and (B). The second blank must reflect Patrick’s intent (ending in failure) to convince people he didn’t mean to offend, so you can eliminate choice (D). The Latin root mal means bad.
 The first blank must emphasize Rodrigo’s efforts, while the second blank must reflect his goal as a loyal friend to end the rumors, thus requiring persistently (tirelessly) and dispel (end) as the answer.
The first blank must emphasize Rodrigo’s efforts, while the second blank must reflect his goal as a loyal friend to end the rumors, thus requiring persistently (tirelessly) and dispel (end) as the answer.
 Do one blank at a time. The second blank, which might seem easier, must reflect his goal as a loyal friend to end the rumors, so you can eliminate choices (B) and (D). The first blank must emphasize his efforts, so you can eliminate choice (A) if you know it. You may need to guess between choices (A) and (C). The Latin root ami means friend, and amiably means in a friendly way.
Do one blank at a time. The second blank, which might seem easier, must reflect his goal as a loyal friend to end the rumors, so you can eliminate choices (B) and (D). The first blank must emphasize his efforts, so you can eliminate choice (A) if you know it. You may need to guess between choices (A) and (C). The Latin root ami means friend, and amiably means in a friendly way.
 The first blank must reflect that Christopher received rare support, while the second blank must mean financial support, thus requiring fortunate and benefactor (supporter) as the answer.
The first blank must reflect that Christopher received rare support, while the second blank must mean financial support, thus requiring fortunate and benefactor (supporter) as the answer.
 Do one blank at a time. The first blank, which might seem easier, must reflect that Christopher received rare support, so you can eliminate choices (A) and (D). The second blank must mean financial support, so you can eliminate choice (C) if you know the word. You may need to guess between choices (B) and (C). The Latin root ben means good.
Do one blank at a time. The first blank, which might seem easier, must reflect that Christopher received rare support, so you can eliminate choices (A) and (D). The second blank must mean financial support, so you can eliminate choice (C) if you know the word. You may need to guess between choices (B) and (C). The Latin root ben means good.
 The first blank must mean clever, while the second blank must relate to a type of comment that is expressed, thus requiring astute (clever) and insights as the answer.
The first blank must mean clever, while the second blank must relate to a type of comment that is expressed, thus requiring astute (clever) and insights as the answer.
 Do one blank at a time. The first blank, which might seem easier, must mean clever, so you can eliminate choices (B) and (C) if you know the words. If not, you will have to rely entirely on the second blank. The second blank must relate to a type of comment that is expressed, so you can eliminate choice (B), as well as choice (D) if you know the word. You may need to guess.
Do one blank at a time. The first blank, which might seem easier, must mean clever, so you can eliminate choices (B) and (C) if you know the words. If not, you will have to rely entirely on the second blank. The second blank must relate to a type of comment that is expressed, so you can eliminate choice (B), as well as choice (D) if you know the word. You may need to guess.
 The first blank must reflect the swaying of low and high tides, while the second blank must mean vast separation, thus requiring fluctuated (swung) and chasm (vast divide) as the answer.
The first blank must reflect the swaying of low and high tides, while the second blank must mean vast separation, thus requiring fluctuated (swung) and chasm (vast divide) as the answer.
 Do one blank at a time. The first blank, which might seem easier, must reflect the swaying of low and high tides, so you can eliminate choices (A) and (C). The second blank must mean vast separation, so you can eliminate choice (D).
Do one blank at a time. The first blank, which might seem easier, must reflect the swaying of low and high tides, so you can eliminate choices (A) and (C). The second blank must mean vast separation, so you can eliminate choice (D).