15
THE SORCERER’S MINIATURE GÖDELIAN LANGUAGE

“TODAY,” said the Sorcerer, “I want to show you a miniature version of Gödel’s famous incompleteness theorem. It will serve as a bridge from what we did last time to what we’ll get into a bit later. The system I will now present is a modernized and streamlined version of a Smullyan ‘language,’ I shall use the quotationless method I showed you last time in place of Smullyan’s one-sided quotation.

(1) PX asserts that X is provable.

(2) QX asserts that X is not provable.

(3) ṖX asserts that XX is provable.

(4) X asserts that XX is not provable.

“We see that the system is self-referential in that it proves various sentences that assert what the system can and cannot prove. We are given that the system is wholly accurate in that every sentence provable in the system is true—in other words the following four conditions hold (where X is any expression).

C₁: If PX is provable so is X.

C₂: If QX is provable then X is not provable.

C₃: If ṖX is provable so is XX.

C₄: If X is provable then XX is not provable.

“Now, just because every sentence provable in the system is true, it doesn’t necessarily follow that every true sentence is provable in the system. As a matter of fact, there happens to be a sentence that is true but not provable in the system. Can you find it?”

• 1 •

Find a true sentence that is not provable in the system.

Refutable Sentences “For each sentence, we define its conjugate as follows. The conjugate of PX is QX, and the conjugate of QX is PX. The conjugate of ṖX is X and the conjugate of X is ṖX. Thus the sentences PX and QX are conjugates of each other, and the sentences ṖX and X are conjugates of each other. Given any conjugate pair, it is obvious that one of the pair is true and the other false.

“A sentence is called refutable (in the system) if its conjugate is provable (in the system). Thus, PX is refutable if and only if QX is provable, and PX is provable if and only if QX is refutable. Likewise with ṖX and X.”

• 2 •

Find a sentence that asserts that it is refutable.

• 3 •

Find a sentence that asserts that it is not refutable.

• 4 •

What sentence asserts that it is provable?

Undecidable Sentences. “A sentence is called undecidable (in the system) if it is neither provable nor refutable in the system,” said the Sorcerer. “Now, as you saw in the solution of Problem 1, the sentence is true but not provable in the system. Since it is true, then its conjugate Ṗ is false, hence also not provable in the system. Thus the sentence is undecidable in the system.

“My argument has appealed to the notion of truth, but even without appeal to this notion one can obtain the undecidability of as a direct consequence of conditions C₁ through C₄ as follows: Suppose were provable. Then by C₄, taking for X, the repeat of is not provable, which means that is not provable. So if is provable, then it is not provable, which is a contradiction. Therefore, is not provable. If its conjugate Ṗ were provable, then by C₃ (taking for X) would be provable, which we just saw is not the case. And so Ṗ is not provable either. Thus the sentence is undecidable in the system.”

“Tell me this,” said Annabelle. “Is the only sentence that is true but unprovable, or are there others?”

“The sentence ,” replied the Sorcerer, “is the only sentence that I know of having the property that for every system satisfying conditions C₁ through C₄, it is true for that system and unprovable in that system. But, as you will see later, for any system satisfying C₁ through C₄, there are other sentences that are true but unprovable in that system. The sentence is, as I said, the only sentence that I know that simultaneously works for all systems satisfying C₁ through C₄.”

The Sorcerer then gave the following problems:

5 • Some Fixed-Point Properties

Show that for any expression E there is a sentence X that asserts that EX is provable (X is true if and only if EX is provable) and there is some X that asserts that EX is not provable.

6 • Some Anti-Fixed-Point Properties

For any sentence X, let be the conjugate of X.

Show that for any expression E there is some sentence X that asserts that E is provable and a sentence X that asserts that E is not provable.

Next, the Sorcerer presented some problems in cross-reference.

• 7 •

Find sentences X and Y such that X asserts that Y is provable and Y asserts that X is not provable. (There are two solutions.) Then show that at least one of the sentences X, Y must be true but not provable (though there is no way to tell which).

• 8 •

Now find sentences X and Y such that X asserts that Y is refutable and Y asserts that X is not refutable. (There are two solutions.) Then show that at least one of the two must be false but not refutable (though there is no way to tell which).

• 9 •

Find sentences X and Y such that X asserts that Y is provable and Y asserts that X is refutable. (There are two solutions.) Then show that one of them is true and not provable, or the other is false but not refutable. Which of X, Y is which?

• 10 •

Find sentences X and Y such that X asserts that Y is not provable and Y asserts that X is not refutable. Does it follow that one of them must be undecidable?

• 11 •

Find sentences X, Y, and Z such that X asserts that Y is refutable, Y asserts that Z is not refutable and Z asserts that X is provable. Is one of the three necessarily undecidable?

• 12 •

“I have said before,” said the Sorcerer, “that for any system satisfying conditions C₁ through C₄, there are sentences other than that are true but unprovable in the system. You are now in a position to prove this. Do you see how?”

Regularity. “I shall call a system regular,” said the Sorcerer, “if the converses of conditions C₁ and C₃ hold—that is, if X is provable, so is PX and if XX is provable, so is ṖX. This together with C₁ and C₃ tell us that PX is provable if and only if X is provable, and ṖX is provable if and only if XX is provable. I might remark that regularity is the analogue of a condition that does hold for the type of systems studied by Gödel, but I’ll say more about that another time. Regular systems have some interesting properties, as you will soon see.

“Let me define a positive sentence as one of the form PX or ṖX and a negative sentence as one of the form QX or X. Positive sentences assert that certain sentences are provable; negative sentences assert that certain sentences are not provable. Let us now note that if the system is regular, then all true positive sentences are provable, and conversely, if all true positive sentences are provable, then the system is regular.”

• 13 •

Why is it that the system is regular if and only if all true positive sentences are provable?

“And so,” continued the Sorcerer, “we see that in a regular system, only negative sentences can be true but unprovable. Any sentence that asserts that something is provable, if true, must itself be provable.”

• 14 •

If a system is regular, does it necessarily follow that every false negative sentence is refutable?

“Regular systems have some interesting features,” said the Sorcerer, “as you will now see.”

• 15 •

“For one thing, in a regular system, the ambiguities of Problems 7 through 10 disappear—that is, if we assume the system is regular, then in Problem 7 we can tell whether it is X or Y that is true but unprovable. Which is it? And in Problem 8, is it X or Y that is false but not refutable? And for Problem 9, is it X that is true but provable, or is it Y that is false but not refutable? And for Problem 10, is it X that is undecidable? All this, of course, with the assumption of regularity.”

“Let us note,” said the Sorcerer, “that for any system satisfying our given conditions C₁ through C₄, whether the system is regular or not, if E is any string of P’s, then if EX is provable, so is X. This follows by repeated applications of C₁. For example, if PPPX is provable, so is PPX (by C₁); hence so is PX (again by C₁); hence so is X (again by C₁). You can readily see that the same holds if E contains four or more P’s—or if E contains two P’s or just one P. And so if E is any string of P’s, if EX is provable, so is X. For a regular system, the converse also holds—that is, if X is provable, so is EX, where E is any string of P’s. For if X is provable and the system is regular, then PX is provable (by regularity); hence so is PPX, and so forth. And so for a regular system, if E is any string of P’s, then EX is provable if and only if X is provable.

“Another thing about regular systems is this: For any system satisfying C₁ through C₄, ṖX is true if and only if PXX is true, for each is true if and only if XX is provable. However, without regularity, there is no reason to believe that ṖX is provable if and only if PXX is provable. If either one is provable, then the other one is true, but that doesn’t mean that the other one is provable. However, if the system is regular, then ṖX is provable if and only if PXX is provable.”

• 16 •

Why is it that in a regular system, ṖX is provable if and only if PXX is provable?

“Now comes a particularly interesting thing about regular systems,” said the Sorcerer. “We have already seen that in any system satisfying conditions C₁ through C₄, there are infinitely many sentences that are true for the system but not provable in the system. But this does not mean that there are infinitely many sentences such that each one is true for all systems satisfying C₁ through C₄ and at the same time unprovable for all such systems. However, there are infinitely many sentences X such that for every regular system satisfying C₁ through C₄, each X is true for the system but unprovable in the system.”

• 17 •

Can you prove this?

“What I have shown you today,” said the Sorcerer, “has applications to the field known as metamathematics—the theory of mathematical systems. My miniature system provides one approach to Gödel’s famous incompleteness theorem:

“Let us consider a mathematical system (M) in which there are well-defined rules specifying certain sentences as true and others as provable in (M), and suppose that we wish to know whether (M) is complete in the sense that all true sentences of (M) are provable in (M). Now it can be shown that if (M) is any one of a wide variety of systems investigated by Kurt Gödel, it is possible to translate my system into (M) in the sense that corresponding to each sentence X of my system, there is a sentence X° of the system (M) such that X is true in my system if and only if the corresponding sentence X° of (M) is a true sentence of (M), and also, X is provable in my system if and only if X° is provable in (M). Do you realize the ramifications of this? It means that for every such system (M), there must be a true sentence of (M) that is not provable in (M)—its truth can be known only by going outside of the system. Thus, no system (M) into which my system is translatable can possibly be complete. Do you see why this is so?”

• 18 •

Why is this so?

All this is most remarkable!” said Annabelle.

“It certainly is!” agreed Alexander.

“What will you tell us about next time?” asked Annabelle.

“On your next visit,” replied the Sorcerer with a mischievous smile, “I have a very special paradox prepared for you.”

“I’m looking forward to it,” said Annabelle. “I’ve always been intrigued by paradoxes.”

Solutions

1. The sentence is . It asserts that the repeat of is not provable, but the repeat of is . Hence is true if and only if it is not provable in the system. This means that it is either true and not provable or false and provable. The latter alternative contradicts the given condition that only true sentences are provable in the system. Therefore, the former alternative holds—the sentence is true but not provable in the system. (This sentence is a transcription of Gödel’s famous sentence that asserts its own nonprovability.)

2. Ṗ asserts that the repeat of —which is —is provable. But is the conjugate of Ṗ. And so Ṗ asserts that its conjugate is provable, or, what is the same thing, that it is itself refutable.

3. The sentence is Ṗ. It asserts that the sentence ṖṖ—which is the conjugate of Ṗ—is provable.

4. ṖṖ asserts that it is provable.

5. A sentence X that asserts that EX is provable is ṖEṖ, which asserts that the repeat of EṖ is provable. But the repeat of EṖ is EṖEṖ, which is EX.

A sentence X that asserts that EX is not provable is E.

6. A sentence X that asserts that E is provable is ṖE. A sentence X that asserts that E is not provable is EṖ.

7. One solution can be obtained by taking X such that it asserts that QX is provable and then taking Y = QX (which asserts that X is not provable). This gives the solution

X = ṖQṖ, Y = QṖQṖ

Another solution can be obtained by taking some Y that asserts that PY is not provable—namely, Y = P and then taking X = PY. We thus have the alternative solution

X = PP, Y = P

In either solution X asserts that Y is provable and Y asserts that X is not provable. Therefore, X is true if and only if Y is provable and Y is true if and only if X is not provable. Now, if X and Y are any two sentences bearing these two relationships with each other, one of them must be true but unprovable by the following argument: Suppose X is provable. Then X is true; hence Y is provable, hence true; hence X is not provable, which is a contradiction. Therefore, X cannot be provable. It then follows that Y must be true. And so, X is definitely not provable and Y is definitely true. Now, either X is true or it isn’t. If X is true, then X is true but not provable. If X is not true, then Y is not provable (because X is true if and only if Y is provable); hence Y is then true but not provable.

In summary, X is not provable and Y is true. If X is true, then it is X that is true but not provable; if X is false, then it is Y that is true but not provable.

(I obtained these solutions by taking for X the conjugate of the Y of the last problem, and for Y, the conjugate of the X of the last problem.)

Now, X asserts that Y is refutable; hence X asserts that is provable; hence asserts that is not provable. Also, Y asserts that X is not refutable; hence Y asserts that is not provable; hence asserts that is provable. Then by the last problem, taking for X and for Y, we see that at least one of , is true but not provable; hence one of X, Y is false but not refutable. (Of course, we could have proved this from scratch—and if the reader has any doubts, he or she might try it—but why duplicate work already done?)

9. One way is to take an X that asserts that P is provable and then take Y = P. Another is to take some Y that asserts that QY is provable and then take X = PY. We thus get the following solutions:

Solution 1: X = ṖP	Y = PP
Solution 2: X = PṖQṖ	Y = ṖQṖ

Suppose X is true. Then Y is provable (as X asserts); hence Y is true; hence X is refutable (as Y asserts), which is not possible. Therefore, X cannot be true; it must be false. Then Y is not provable (as X asserts), and so we now know that X is false and Y is not provable. If X is not refutable, then X is false but not refutable. On the other hand, if X is refutable, then what Y asserts is true; hence Y is then true but not provable. And so, either X is false but not refutable, or Y is true but not provable.

10. We can simply take the conjugates of the X and Y of the last problem and interchange them, thus getting the solutions:

Solution 1: X = QP	Y = P
Solution 2: X = QṖ	Y = QṖQṖ

By applying our analysis of the last problem to and , instead of X and Y respectively, we see that either is false but not refutable, or is true but not provable. This means that either X is false but not refutable or Y is true but not provable.

11. We shall give but one solution, which we get by taking an X that asserts that PQX is provable, then taking Y to be QQX and Z to be PX. Thus X asserts that Y is refutable, Y asserts that QX is not provable, or equivalently that PX is not refutable, but PX is Z. Of course, Z asserts that X is provable. We thus have the following solution:

X = ṖPQṖ Y = QQṖPQṖ Z = PṖPQṖ

Now, suppose Z is true. Then X is provable, hence true; hence Y is refutable, hence false; hence Z is refutable, hence false; and we have a contradiction. Therefore, Z cannot be true; Z is false. Also then, X is not provable. If X is true, then X is true but not provable. Suppose X is false. Then Y is not refutable. If Y is false, then Y is false but not refutable. If Y is true, then Z is not refutable. And so, one of the following three things must hold: (1) X is true but not provable; (2) Y is false but not refutable; (3) Z is false but not refutable.

12. This is immediate from Problem 7. We know that in any system satisfying conditions C₁ through C₄, at least one of the two sentences ṖQṖ, QṖQṖ is true but not provable in the system. Likewise, with the two sentences PP, P. And, of course, our old standby is true but not provable in the system. And so, the system contains at least three sentences that are true but not provable in the system. (Actually, there are infinitely many—for example, one of the three sentences PPPP, PPP, PP must be true but not provable. Also, one of the four sentences PPPPPP, PPPPP, PPPP, PPP is true but unprovable, and so forth.)

13. Suppose the system is regular. Consider a positive sentence X. It is either of the form PY or ṖY. If PY is true, then Y is provable; hence by regularity PY is provable. If ṖY is true, then YY is provable; hence by regularity, ṖY is provable. This shows that regularity implies that all true positive sentences are provable.

Conversely, suppose that all true positive sentences are provable. Well, suppose Y is provable. Then PY is true, hence provable (by hypothesis). Also, if YY is provable, ṖY is true, hence provable (by hypothesis), and so the system is regular.

14. Of course it does! Suppose the system is regular. Now let X be any false negative sentence. Then its conjugate is a true positive sentence, hence provable. Hence, X is refutable.

15. Suppose the system is regular. Then, as we have shown, all true positive sentences are provable in the system and all false negative sentences are refutable.

In Problem 7, X is a positive sentence; hence it is not possible that X is true and unprovable; hence it is definitely Y that is true and unprovable. This goes for either of the two solutions for X and Y. Thus, the sentences QṖQṖ and P are both true and unprovable in every regular system.

In Problem 8, it cannot be Y that is false but not refutable, because Y is a negative sentence, so it must be X.

In Problem 9, it cannot be that Y is true and not provable, since Y is a positive sentence, so it must be that X is false but not refutable.

In Problem 10, it cannot be X that is false and not refutable, since X is a negative sentence, so it is Y that is true but not provable.

16. Suppose the system is regular. Then ṖX is provable if and only if ṖX is true, which in turn is the case if and only if XX is provable, which in turn is the case if and only if PXX is true, which in turn is the case if and only if PXX is provable.

More simply, we know that ṖX is true if and only if PXX is true (the truth of either is equivalent to the provability of XX), but ṖX and PXX are both positive sentences, and for a regular system, truth and provability coincide for positive sentences.

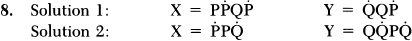
17. If E is any string of P’s, the sentence E must be both true and unprovable for all regular systems. To begin with, even for a system not necessarily regular, EE cannot be provable, for if it were, E would be provable (by repeated applications of C₁); hence EE would not be provable (by C₃), and we would have a contradiction. Therefore, EE is not provable. Hence also E must be true. But now, if we add the assumption that the system is regular, then if E were provable, then EE would also be provable, which is not the case. Therefore, E is not provable in any regular system—yet it is true for all regular systems (satisfying C₁ through C₄, of course).

18. Since there is a true sentence X of the Sorcerer’s system that is not provable in his system (for example, the sentence , as we saw in the solution of Problem 1), then its translation X into (M) must be a true sentence of (M) that is not provable in (M).

15THE SORCERER’S MINIATURE GÖDELIAN LANGUAGE

Solutions

15
THE SORCERER’S MINIATURE GÖDELIAN LANGUAGE