5. Un po’ di metodo

L’onere della prova costituirà, per i matematici greci, uno dei problemi maggiori. Non un solo teorema potrà essere convalidato senza essere accompagnato da una dimostrazione, vale a dire da un preciso ragionamento logico che stabilisca in via definitiva la sua veridicità. E va detto che, senza il vaglio rappresentato dalle dimostrazioni, i risultati matematici possono sempre riservare delle brutte sorprese. Nel senso che certi metodi, pur legittimati nel tempo e ampiamente utilizzati, a volte non funzionano come dovrebbero.

Un esempio. Pensate alla costruzione contenuta nel papiro di Rhind per disegnare un quadrato e un disco di area uguale. Ebbene, è sbagliata. Non di molto, certo, ma è comunque sbagliata. Basta misurare con precisione le superfici e si scopre una differenza dello 0,5% circa! Gli agrimensori e altri geometri dei terreni tenderebbero a sorvolare su un discostamento del genere, ma i matematici teorici lo giudicherebbero inammissibile.

Lo stesso Pitagora si lasciò ingannare da ipotesi scorrette. Il suo errore più celebre riguarda le lunghezze commensurabili. Egli pensava infatti che, in geometria, due lunghezze siano sempre commensurabili, ovvero che sia possibile trovare un’unità sufficientemente piccola che permetta di misurarle simultaneamente. Immaginate una linea di 9 centimetri e un’altra di 13,7 centimetri. I greci non conoscevano i numeri decimali, misuravano le lunghezze solo con i numeri interi. Per cui, secondo loro, la seconda linea non si poteva misurare in centimetri. Detto ciò, in questo caso non restava che considerare un’unità dieci volte più piccola, per poter dire che le due linee misurano rispettivamente 90 e 137 millimetri. In sostanza, Pitagora era certo che due linee qualsiasi, indipendentemente dalla loro lunghezza, fossero sempre commensurabili trovando l’unità di misura adeguata.

La sua convinzione venne tuttavia smentita proprio da un pitagorico, Ippaso di Metaponto. Questi scoprì che, nel quadrato, il lato e la diagonale sono incommensurabili! Qualunque sia l’unità di misura prescelta, è impossibile che sia il lato del quadrato sia la sua diagonale siano misurabili con numeri interi. Ippaso ne fornì una dimostrazione logica che non lasciava alcun dubbio in materia. Al che, Pitagora e i suoi discepoli furono talmente contrariati che Ippaso finì per essere escluso dalla scuola. Non solo. Si racconta che la scoperta gli costò anche una mortale spedizione, durante la quale venne gettato in mare dai condiscepoli!

Alle orecchie del matematico, aneddoti del genere suonano angoscianti. Si potrà mai essere sicuri di qualcosa? Si deve vivere nella continua paura che ogni scoperta matematica finisca, un giorno, per essere demolita? E il triangolo 3-4-5? Siamo proprio certi che si tratti di un triangolo rettangolo? Non corriamo magari il rischio di scoprire, un bel giorno, che l’angolo che sembrava fino a quel momento perfettamente retto non lo sia, anche lui, solo approssimativamente?

Ancora adesso, non è raro che i matematici cadano vittime di intuizioni ingannevoli. Ecco perché, perseguendo la ricerca del rigore dei loro omologhi greci, i nostri matematici oggi come oggi prestano la massima cura nel differenziare gli enunciati dimostrati, che chiamano “teoremi”, da quelli che ritengono veri ma per i quali non hanno ancora prove, che chiamano “congetture”.

Una delle più famose congetture del nostro tempo è l’ipotesi di Riemann. Non sono pochi i matematici che considerano tale ipotesi, non dimostrata, abbastanza vera tanto da porla a fondamento delle loro ricerche. Se la congettura di Riemann diventasse, un giorno, teorema, tutti i loro lavori ne risulterebbero legittimati. Ma se, viceversa, fosse un giorno smentita, ecco che le opere di intere vite di ricerca sprofonderebbero nel nulla con essa. I nostri scienziati del XXI secolo sono indubbiamente più ragionevoli dei loro antenati greci, ma è facile capire che, in una situazione del genere, un matematico che annunciasse l’erroneità dell’ipotesi di Riemann susciterebbe in alcuni colleghi l’identica voglia di annegarlo che costò la vita a Ippaso.

In sostanza, per sottrarsi all’angoscia permanente della smentita, i matematici hanno un assoluto bisogno di dimostrazioni. No, per carità, non scopriremo mai che il 3-4-5 non è un triangolo rettangolo. Lo è di sicuro. E una tale certezza deriva dal fatto che il teorema di Pitagora è stato dimostrato. Ricordate? Ogni triangolo in cui la somma dei quadrati costruiti sui due cateti è uguale al quadrato costruito sul terzo lato si dice triangolo rettangolo. Un enunciato che per i mesopotamici era certo solo una congettura. E che, con i greci, è diventato un teorema. E così sia.

Ma, allora, a che cosa somiglia una dimostrazione? Il teorema di Pitagora non è soltanto il più celebre dei teoremi, è anche uno di quelli che contano il maggior numero di dimostrazioni diverse. Parecchie decine. Alcune di esse sono state scoperte in maniera indipendente da civiltà che non avevano mai sentito parlare né di Euclide né di Pitagora. È il caso delle dimostrazioni trovate nei commenti ai Nove capitoli cinesi. Altre sono opera di matematici che conoscevano il teorema già provato ma che, per un senso di sfida o per lasciare una propria impronta personale, si sono divertiti a cercare altre prove. Tra costoro, spiccano nomi celebri, come quelli del genio italiano Leonardo da Vinci o del ventesimo presidente degli Stati Uniti, James Abram Garfield.

Uno dei principi ricorrenti in molte di queste dimostrazioni è quello del puzzle: se due figure geometriche possono costituirsi a partire dagli stessi elementi, vuol dire che hanno la stessa superficie. Osservate la composizione immaginata dal matematico cinese del III secolo Liu Hui.

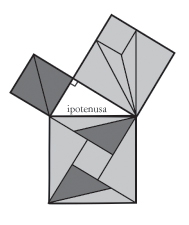
I due quadrati costruiti sui due cateti dell’angolo retto del triangolo rettangolo centrale si compongono rispettivamente di due e cinque pezzi: esattamente i sette pezzi che vanno a comporre il quadrato costruito sull’ipotenusa. La superficie del quadrato costruito sull’ipotenusa è dunque uguale alla somma delle superfici dei due quadrati minori. E poiché la superficie di un quadrato è uguale al numero quadrato associato alla lunghezza del suo lato, è così dimostrato che il teorema di Pitagora è vero.

Trascuriamo pure, qui, certi dettagli. Basti dire che, perché la dimostrazione sia completa, bisogna comprovare che tutti i pezzi sono rigorosamente identici e che tale suddivisione vale per tutti i triangoli rettangoli.

E ora possiamo riprendere il filo delle nostre deduzioni. Perché 3-4-5 è un triangolo rettangolo? Perché verifica il teorema di Pitagora. E perché il teorema di Pitagora è vero? Perché la suddivisione di Liu Hui mostra che il quadrato costruito sull’ipotenusa è formato dai medesimi pezzi dei quadrati costruiti sui lati dell’angolo retto. Sembra il “gioco dei perché” che piace tanto ai bambini. Il problema è che quel gioco ha un brutto difetto: non finisce mai. Qualunque sia la risposta data a una domanda, si può sempre mettere in discussione la risposta stessa. Perché? Perché sì.

Torniamo al nostro puzzle. Abbiamo detto che figure composte a partire dagli stessi pezzi hanno la stessa superficie. Ma non abbiamo ancora dimostrato che il principio è sempre vero. Non si potrebbero trovare dei pezzi del puzzle la cui superficie varia a seconda del modo in cui li si assembla? Sembra una proposizione assurda, no? Talmente assurda che sarebbe illogico tentare di dimostrarla... Eppure abbiamo appena rilevato che, in matematica, è importante dimostrare tutto. Saremmo disposti, noi, a rinunciare a nostri principi, pochi istanti dopo averli sposati?

La situazione è grave. Tanto più che, se riusciamo a spiegare perché il principio del puzzle è vero, dovremo poi giustificare comunque il ragionamento impiegato per arrivare alla spiegazione data!

I matematici greci hanno ben presente il problema. Per eseguire una dimostrazione, si deve cominciare da qualche parte. Ebbene, il primo enunciato di ogni opera di matematica non può essere stato dimostrato, proprio perché è il primo. Ogni costruzione matematica deve dunque cominciare con l’ammettere un certo numero di elementi già conosciuti. Elementi che faranno da fondamento a tutte le deduzioni successive, e che quindi vanno selezionati con la massima cura.

Questi elementi di base i matematici li chiamano “assiomi”. Gli assiomi sono enunciati matematici come possono esserlo i teoremi e le congetture. A differenza di questi ultimi, però, non sono dimostrabili e non vogliono esserlo. Sono ammessi come veri.

Gli Elementi di matematica, redatti da Euclide nel III secolo a.C., costituiscono un insieme di tredici libri che trattano principalmente di geometria e aritmetica.

Di Euclide sappiamo poco, e le fonti che lo riguardano sono molto più rare rispetto a quelle su Talete o Pitagora. Forse è vissuto dalle parti di Alessandria. Ma, secondo alcuni, può anche darsi che, come nel caso di Pitagora, non sia mai esistito realmente, e che Euclide sia il nome di un collettivo di sapienti. Nulla di meno sicuro.

Malgrado le scarse informazioni che abbiamo sulla sua persona, Euclide ci ha lasciato, con i suoi Elementi, un’opera monumentale, unanimemente considerata uno dei più grandi testi della storia della matematica. Proprio perché è stato il primo ad adottare un approccio assiomatico. La costruzione degli Elementi è straordinariamente moderna, e la sua struttura è assai vicina a quella ancora utilizzata dai matematici del nostro tempo. Alla fine del XV secolo, gli Elementi saranno tra le prime opere a essere stampate dalla neonata tipografia Gutenberg. Di più. Oggi come oggi, l’opera di Euclide sarebbe il testo con il maggior numero di edizioni della storia, secondo solo alla Bibbia.

Nel primo libro degli Elementi, che tratta la geometria piana, Euclide enumera i cinque assiomi seguenti.

1. Tra due punti qualsiasi è possibile tracciare una ed una sola retta.

2. Si può prolungare una retta oltre i due punti indefinitamente.

3. Dato un segmento, è possibile descrivere un cerchio il cui raggio è il segmento stesso e il cui centro è una delle sue estremità.

4. Tutti gli angoli retti sono tra loro congruenti.

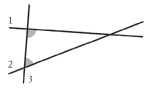
5. Se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, le due rette si incontreranno da quello stesso lato.7

Ai cinque assiomi fa seguito un’intera sfilza di teoremi, tutti impeccabilmente dimostrati. Per ognuno di essi, Euclide utilizza sempre e soltanto i cinque assiomi o i loro risultati stabiliti in precedenza. L’ultimo teorema del primo libro è una nostra vecchia conoscenza: si tratta del teorema di Pitagora.

Dopo Euclide, numerosi matematici affronteranno a loro volta il problema della scelta degli assiomi. Molti rimasero intrigati e disorientati specialmente dal quinto. L’ultimo assioma, infatti, è assai meno elementare dei primi quattro. Tanto che verrà a volte sostituito da un altro enunciato più semplice, che consente in ogni caso di giungere alle medesime conclusioni: per un punto, è possibile tracciare una e una sola retta parallela a una data retta. Le discussioni sulla scelta del quinto assioma sono durate fino al XIX secolo, finendo per risolversi nella creazione di nuovi modelli geometrici secondo i quali l’assioma risulterebbe falso!

L’enunciato degli assiomi pone anche un altro problema: quello delle definizioni. Tutti i termini impiegati – punti, segmenti, angoli o cerchi – che cosa significano? Come per le dimostrazioni, il problema delle definizioni è di per sé infinito. La prima definizione data deve infatti essere espressa usando termini che non sono mai stati definiti in precedenza.

Negli Elementi, le definizioni precedono dunque gli assiomi. Esempio: l’incipit del primo libro riguarda la definizione del punto:

Il punto è ciò che non ha parti.

Dopodiché, sbrigatevela voi! Euclide, con una tale definizione, intende dire che il punto è la più piccola figura geometrica possibile. Impossibile, con un punto, comporre dei puzzle. Il punto non si può tagliare. Non ha parti. Nel 1632, in una delle prime edizioni francesi degli Elementi, il matematico Denis Henrion amplia un po’ la definizione precisando, nei suoi commenti, che il punto non ha né lunghezza né larghezza né profondità.

Le definizioni negative lasciano nondimeno scettici. Dire che cosa il punto non è non equivale a dire che cos’è! Ciononostante, tanti complimenti a chi saprebbe proporre qualcosa di meglio. In alcuni manuali scolastici dell’inizio del XX secolo si trova, a volte, la seguente definizione: un punto è la traccia lasciata da una matita finemente appuntita e appoggiata su un foglio di carta. Finemente appuntita! Una volta tanto ci muoviamo sul piano del concreto. La definizione avrebbe fatto balzare sulla sedia Euclide, Pitagora e Talete, che tanto si erano dannati per cercare di rendere le figure geometriche oggetti astratti e idealizzati. Nessuna matita, per quanto finemente appuntita, sarebbe in grado di lasciare una traccia che davvero non abbia né lunghezza né larghezza né profondità.

In sostanza, nessuno sa dire con certezza che cos’è un punto, anche se tutti sono più o meno convinti che l’idea del punto sia abbastanza semplice e chiara da non suscitare particolari ambiguità. Quando impieghiamo il termine punto, siamo tutti più o meno sicuri di fare riferimento alla stessa cosa.

Insomma. Tutta la geometria si fonderà su un tale atto di fede, nelle definizioni primarie e negli assiomi. E, in mancanza di meglio, tutta la matematica moderna finirà per costruirsi su questo medesimo modello.

Definizioni – Assiomi – Teoremi – Dimostrazioni: il cammino tracciato da Euclide determina quella che sarà la routine dei matematici successivi. Tuttavia, man mano che si strutturano e si sviluppano le diverse teorie, sulla strada dei matematici si vanno interponendo nuovi intoppi: i paradossi.

Un paradosso è un ingranaggio che dovrebbe funzionare ma non funziona. È una contraddizione apparentemente insolubile. Un ragionamento che sembra perfettamente corretto e che invece dà luogo a un risultato del tutto assurdo. Come se voi stabiliste una lista di assiomi che vi paiono incontestabili e ne ricavaste, al contrario, dei teoremi chiaramente falsi. Un incubo!

Uno dei più celebri paradossi è attribuito a Eubulide di Mileto e riguarda discorsi tenuti dal poeta Epimenide. Il quale, un giorno, avrebbe dichiarato che “i cretesi sono dei bugiardi”. Il problema consiste nel fatto che Epimenide era cretese! Di conseguenza, se quanto sta dicendo è vero, è lui il primo bugiardo... e quel che dice è quindi falso. Se invece la sua frase fosse falsa, Epimenide mentirebbe e sarebbe la frase stessa a dire il vero! Dopo di lui, saranno inventate molte varianti del medesimo paradosso, la più semplice delle quali consiste nella frase di una persona che semplicemente dichiara: “Io sono un bugiardo.”

Il paradosso del mentitore chiama in causa un’idea precostituita, secondo la quale ogni frase deve essere o vera o falsa – e non esisterebbe una terza possibilità. In matematica si chiama principio del terzo escluso. A prima vista, verrebbe la tentazione di promuovere un tale principio ad assioma. Ma il paradosso del mentitore ci mette dovutamente in guardia: la situazione è più complicata di quanto non appaia. Se un enunciato arriva ad affermare la propria erroneità, la logica ci dice che lo stesso enunciato non può essere né vero né falso.

Tale paradosso non impedirà a gran parte dei matematici, fino ai giorni nostri, di considerare vero il suddetto terzo escluso. In fondo, il paradosso del mentitore non è esattamente un enunciato matematico. Lo si potrebbe ritenere, più che una contraddizione logica, un’incoerenza linguistica. Eppure, più di duemila anni dopo Eubulide, alcuni logici scopriranno che paradossi dello stesso tipo possono anche integrarsi con le teorie più rigorose. Una scoperta che getterà i matematici nel più profondo scompiglio.

Il greco Zenone di Elea, vissuto nel V secolo a.C., è divenuto anche lui maestro nell’arte di creare paradossi. Se ne annoverano circa una decina. Uno dei più celebri è quello di Achille e la tartaruga.

Immaginate una corsa tra Achille, il “piè veloce”, e una tartaruga. Per partire alla pari in quanto a possibilità di vincere, alla tartaruga viene concesso un certo margine di vantaggio: diciamo un centinaio di metri. Ciononostante, si dà per scontato che Achille, correndo molto più rapidamente della tartaruga, prima o poi la raggiungerà. Invece no. Zenone afferma il contrario.

Dividiamo il percorso in più tappe, dice il filosofo. Per poter raggiungere la tartaruga, Achille deve correre almeno i cento metri che la separano da lui. Ma, nel tempo che impiegherà per coprire i cento metri, la tartaruga sarà a sua volta avanzata un po’, per cui Achille, per raggiungerla, dovrà fare più strada. E nel tempo che gli è stato necessario per coprire quel tanto di percorso, la tartaruga si sarà allontanata ancora un po’. Dovrà allora percorrere ancora un pezzetto di tragitto, al termine del quale la tartaruga sarà avanzata di nuovo.

In sostanza, ogni volta che Achille raggiunge il punto precedentemente occupato dalla tartaruga, questa sarà avanzata un po’ di più, quanto basta per non essere mai raggiunta. E il tutto resta valido qualunque sia il numero di tappe considerato! Per cui Achille sembra condannato ad avvicinarsi sempre più alla tartaruga senza mai poterla superare.

Assurdo, vero? Basta infatti fare una prova pratica per verificare che il corridore supererà la tartaruga senza problemi. Eppure il ragionamento di Zenone sembra reggere, e non è tanto facile rintracciarvi un errore logico.

I matematici impiegheranno un sacco di tempo per comprendere questo paradosso, il quale sfida abilmente il concetto di infinito. Se i corridori procedono in linea retta, la loro traiettoria può essere assimilata a quella che Euclide chiama segmento. Un segmento possiede una lunghezza finita anche se è composto da un numero infinito di punti che hanno una lunghezza pari a zero. In qualche modo, esiste dunque, nel finito, un infinito. Il paradosso di Zenone suddivide l’intervallo di tempo coperto da Achille per raggiungere la tartaruga in un’infinità di intervalli sempre più piccoli. Un’infinità di tappe che dura comunque per un tempo finito, per cui nulla impedisce ad Achille di raggiungere la tartaruga una volta che esso è trascorso.

La nozione di infinito in matematica diventerà, senza dubbio, la maggior fonte di paradossi, ma sarà, al tempo stesso, la culla delle teorie più affascinanti.

Nella storia, i matematici intratterranno, con i paradossi, rapporti ambigui. Da un lato, essi rappresentano il loro maggior pericolo. È sufficiente che, un dato giorno, una teoria dia luogo a un paradosso perché tutti i suoi fondamenti, e con essi tutti i teoremi che si credevano costruiti sui suoi assiomi, crollino. Dall’altro, però, che bella sfida! I paradossi sono una fonte ricchissima ed entusiasmante di rimessa in discussione dell’esistente. Se insorge un paradosso, vuol dire che ci è sfuggito qualcosa. Vuol dire che abbiamo interpretato male una nozione, enunciato male una definizione, scelto male un assioma. Vuol dire che abbiamo scambiato per indubitabile una cosa che non lo era affatto. I paradossi costituiscono un invito all’avventura. Un invito a ripensare le nostre più intime certezze. Quante nuove idee e quante teorie originali avremmo sfiorato se non ci fossero stati i paradossi a spingerci verso di loro?

I paradossi di Zenone ispireranno nuove concezioni relative all’infinito e alla misura. E il paradosso del mentitore coinvolgerà i logici in una ricerca sempre più minuziosa dei concetti di verità e dimostrabilità. Ancora oggi, molti ricercatori scandagliano nozioni matematiche che si trovavano già, allo stato embrionale, nei paradossi dei sapienti greci.

Nel 1924 i matematici Stefan Banach e Alfred Tarski svelarono un paradosso che reca oggi il loro nome e che rimette in discussione il principio stesso dei puzzle. Per quanto ovvio possa sembrare, questo principio può essere contraddetto. Banach e Tarski sono stati capaci di descrivere un puzzle a tre dimensioni il cui volume, a seconda dei modi in cui si incastrano i pezzi, non è lo stesso! Vi torneremo su. I pezzi da loro immaginati, tuttavia, sono talmente strani e difformi da non avere nulla in comune con le figure geometriche contemplate dai geometri greci. Tranquilli, però. Il principio dei puzzle resta comunque valido, quantomeno con pezzi che ricalcano le forme dei triangoli, del quadrato o di altre figure geometriche classiche. E la prova di Liu Hui del teorema di Pitagora regge ancora.

Ma il tutto ci serva da lezione! Diffidiamo delle certezze acquisite e lasciamoci invece stupire e sorprendere dai misteri di quel mondo matematico che gli scienziati greci hanno scoperto per noi.

7 L’assioma, molto più complesso degli altri quattro, susciterà tra i matematici non poche discussioni. Nella figura qui sotto, la somma dei due angoli indicati è inferiore a quella di due angoli retti, per cui le rette 1 e 2 si incontrano dal lato in cui sono posizionati i due angoli.