7. Niente e meno di niente

Dall’alto dei suoi 6714 metri d’altezza, il monte Kailash, in Tibet, fa parte del cerchio ristretto di cime non ancora scalate dall’Homo sapiens. Il suo profilo arrotondato, striato di neve sul grigio del granito, si staglia massiccio sopra il paesaggio smussato dell’Ovest himalayano. Per gli abitanti della regione, indù o buddisti che siano, la montagna è sacra, e reca il suo florilegio di miti ancestrali e di storie meravigliose. Si racconta, tra l’altro, che si tratti del leggendario monte Meru, il quale, secondo le mitologie locali, costituirebbe il centro dell’Universo.

È qui che si nasconde la sorgente di uno dei sette fiumi sacri della regione: l’Indo.

Scaturendo da lassù e scendendo dalle pendici del monte Kailash, l’Indo volge in direzione est, facendosi strada a gran velocità tra le montagne del Kashmir, per poi iniziare a scorrere più lentamente verso sud. Qui attraversa le pianure del Punjab e del Sind dell’attuale Pakistan, per poi diventare delta e gettarsi nel mare Arabico. La valle dell’Indo è fertile. Durante l’Antichità, la regione è coperta di foreste rigogliose e fruscianti. Gli elefanti d’Asia vi convivono con i rinoceronti, le tigri del Bengala, le scimmie schiamazzanti e i serpenti, che gli incantatori si apprestano ad ammaliare con i loro flauti. Sbucando da un sentiero, quasi quasi ci si aspetterebbe d’incontrare Mowgli, il cucciolo d’uomo del Libro della giungla, le cui avventure hanno come sfondo scenari del genere. Ed è lì che nascerà una civiltà originale e appartata, i cui matematici svolgeranno un ruolo determinante all’inizio del Medioevo.

Nel III millennio a.C., vedono la luce, attorno al fiume, alcune importanti città, come Mohenjo-Daro o Harappa. Città che, viste da lontano, somigliano un poco, costruite come sono con mattoni d’argilla, a quelle contemporanee della Mesopotamia. Nel II millennio a.C. ha inizio l’epoca vedica. La regione viene suddivisa in una quantità di piccoli regni, che si moltiplicano verso est fino alle rive del Gange. L’induismo nasce, si sviluppa e vengono composti i primi grandi testi in sanscrito. Nel IV secolo a.C., Alessandro Magno raggiunge le rive dell’Indo e vi fonda due città che prendono il nome di Alessandria, senza peraltro conoscere il prestigioso destino di Alessandria d’Egitto. Ma è comunque lì che trasmigra una parte della cultura greca, integrandosi con le culture locali. Dopodiché giunge l’epoca dei grandi imperi. I Maurya regnano sulla quasi totalità del subcontinente indiano per un secolo abbondante. E ai Maurya succede tutta una sfilza di dinastie, coesistenti in termini più o meno pacifici, fino alla conquista musulmana dell’VIII secolo.

In questo periodo storico, gli indiani fanno matematica, anche se, purtroppo, non ne sappiamo granché. Per una semplice ragione: i loro uomini di scienza hanno sviluppato, fin dall’inizio dell’epoca vedica, un ideale di trasmissione delle conoscenze orale, che bandisce, per principio, la messa per iscritto. I saperi devono essere trasmessi a voce, di generazione in generazione, da maestro ad allievo. I testi s’imparano a memoria, sotto forma di poemi o accompagnati da astuzie mnemotecniche, poi recitati e ripetuti per quante volte sia necessario affinché siano perfettamente padroneggiati. È vero che, qua e là, affiorano eccezioni alla regola, frammenti scritti a noi pervenuti, ma si tratta di una quantità esigua.

Con tutto ciò, gli indiani fanno matematica! Come spiegare, altrimenti, la ricchezza di concetti di cui ci renderanno partecipi quando, intorno al V secolo, decidono finalmente di passare alla traduzione per iscritto dei saperi accumulati oralmente da secoli? Anzi, l’India, d’ora in avanti, vive un’età dell’oro della scienza i cui effetti s’irradieranno ben presto nel mondo intero.

Gli scienziati indiani si adoperano a scrivere lunghi trattati in cui riprendono le conoscenze tramandate dalle precedenti generazioni completandole con gli esiti delle nuove scoperte. Uno dei più famosi è Aryabhata, che s’interessò all’astronomia e al calcolo, con un notevole grado di approssimazione, del numero π. Varāhamihira realizzò nuovi progressi in trigonometria. Bhāskara fu il primo a scrivere lo zero in forma di circolo e a utilizzare scientificamente il sistema decimale da noi impiegato ancora oggi. Eh sì, le nostre dieci cifre, 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, che abitualmente chiamiamo numeri arabi, sono in realtà indiani!

Qualora, poi, si volesse ricordare un nome tra tutti gli scienziati indiani del tempo, la scelta della Storia cadrebbe sicuramente su quello di Brahmagupta, il quale visse nel VII secolo e fu direttore dell’osservatorio di Ujjain. All’epoca, la città di Ujjain, situata sulla riva destra del fiume Shipra, al centro dell’odierna India, era uno dei maggiori centri scientifici del paese. Il suo osservatorio astronomico era celebre, e la città era già nota a Claudio Tolomeo al tempo della grande Alessandria.

Nel 628, Brahmagupta pubblica la sua opera più importante, il Brāhmasphuţasiddhānta, in cui si trova la prima descrizione completa dello zero e dei numeri negativi, accompagnata dalle loro proprietà aritmetiche.

Oggi, lo zero e i numeri negativi sono divenuti così onnipresenti nella nostra vita quotidiana – per misurare la temperatura, l’altitudine sul livello del mare o il saldo del nostro conto in banca – che rischiamo di dimenticare di quali idee geniali essi siano espressione! La loro invenzione è stata un esercizio di acrobazia cerebrale poco comune, che gli scienziati indiani hanno eseguito per primi, alla perfezione.

Comprenderne il processo, in cui tutto appare sottile e potente al tempo stesso, rappresenta una delizia intellettuale su cui sarà bene soffermarsi un poco, se si vogliono capire più a fondo i rivolgimenti interni alla matematica che segneranno i secoli successivi.

Una delle domande che mi viene posta con maggior frequenza, quando parlo in pubblico della mia passione per la matematica, è come sia nata in me. “Come le è venuto questo pallino a dir poco bizzarro?” mi chiedono ogni tanto. “È stato un professore speciale a trasmetterle questa passione?” “La matematica le piaceva già da bambino?” La manifestazione di una vocazione simile non smette di risvegliare la curiosità di persone per le quali tale disciplina è sempre rimasta un mistero.

Ebbene, in tutta onestà, devo ammettere che non lo so. Più vado indietro nel tempo con la mente, più mi rendo conto di aver sempre amato la matematica, senza però riuscire a individuare un evento specifico della mia vita che abbia fatto da incentivo. Anche se, frugando meglio nella memoria, riaffiorano certi episodi di puro godimento intellettuale, che perlopiù coincidevano con l’improvvisa comparsa di idee nuove. Un esempio, in dettaglio. La scoperta, da parte mia, di una sorprendente proprietà della moltiplicazione.

Dovevo avere 9 o 10 anni, quando, digitando un po’ a caso sulla mia calcolatrice di scolaro, mi sono imbattuto in uno strano risultato: 10 × 0,5 = 5. Moltiplica il numero 10 per 0,5 e otterrai 5. Questo osava dirmi la mia calcolatrice, nella quale allora riponevo una fiducia tanto cieca quanto irragionevole. Com’è possibile che, moltiplicando un numero, si ottenga un numero più piccolo? Moltiplicare non vuol forse dire aumentare una quantità? Non si trattava di una vera e propria contraddizione al significato stesso del verbo “moltiplicare”? La mia cara calcolatrice non avrebbe dovuto presentarmi un numero superiore a 10?

Mi ci è voluto del tempo, parecchie settimane spese a ripensarci di continuo, per riuscire a chiarirmi le idee. Il lampo risolutivo si è manifestato il giorno in cui ho pensato di raffigurare la moltiplicazione in maniera geometrica, ripercorrendo senza saperlo i passi degli antichi pensatori. Si prenda un rettangolo la cui lunghezza misuri 10 unità e la larghezza 0,5. La sua superficie sarà quella di 5 piccoli quadrati di lato 1.

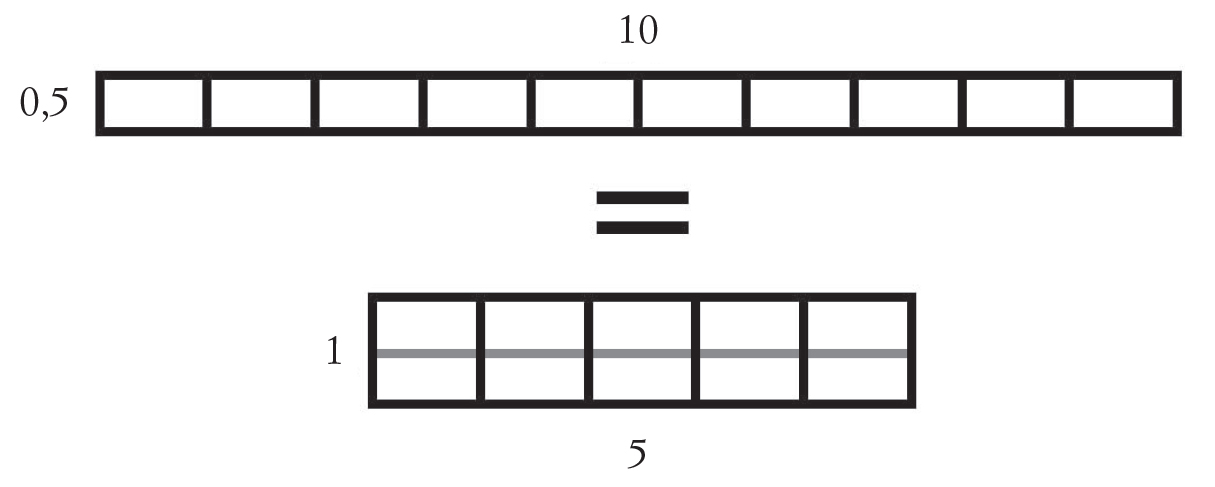
In altri termini, moltiplicare per 0,5 vuol dire dividere per 2. E il medesimo principio si applica a tanti altri numeri. Moltiplicare per 0,25 vuol dire dividere per 4; moltiplicare per 0,1 vuol dire dividere per 10, e così via.

La spiegazione è convincente, la sua conclusione presenta nondimeno un lato sconcertante: la parola “moltiplicazione” non ha, in matematica, esattamente lo stesso significato che ha nel linguaggio corrente. Chi, nella vita di tutti i giorni, arriverebbe a credere di aver moltiplicato la superficie del suo giardino dopo averne venduta la metà? Chi oserebbe pensare che la sua fortuna si è moltiplicata dopo averne perso il 50%? Con premesse del genere, la moltiplicazione dei pani diventerebbe un miracolo alla portata di chiunque: mangiatene la metà e il gioco è fatto.

Quando le sviluppate per la prima volta, riflessioni del genere vi solleticano il cervello. Hanno infatti qualcosa di deliziosamente fastidioso, e ci riecheggiano in mente come un gioco di parole particolarmente riuscito. Questo, almeno, è stato l’effetto prodotto da scoperte tanto curiose sul bambino che ero allora. E la loro stranezza mi è apparsa ancor più chiaramente quando, molti anni dopo, leggendo un testo del matematico Henri Poincaré, Scienza e metodo, pubblicato nel 1908, vi ho trovato la seguente frase: “La matematica è l’arte di dare lo stesso nome a cose diverse.”

A dire il vero, bisogna ammettere che la frase può, con ogni probabilità, applicarsi a qualsiasi linguaggio. La parola “frutto”, per esempio, indica cose differenti come mele, ciliegie o pomodori. E ciascuna di queste parole raggruppa a sua volta una moltitudine di varietà diverse, le quali implicheranno delle categorie più piccole, per poco che ci si dedichi a un’analisi botanica abbastanza meticolosa. Eppure, con ragione, Poincaré sottolinea che nessun linguaggio come quello matematico si spinge tanto lontano nel processo di raggruppamento. La matematica consente accostamenti che nessun’altra lingua autorizza. Per i matematici, moltiplicazione e divisione non sono che un’unica e identica operazione. Moltiplicare per un numero equivale a dividere per un altro. Tutto dipende dal punto di vista adottato.

L’invenzione dello zero e dei numeri negativi è ispirata dal medesimo atteggiamento intellettuale. Per crearli, occorre avere il coraggio di pensare le cose in contraddizione con la propria stessa lingua. Occorre raggruppare in una medesima idea concetti che il linguaggio tratta in maniera radicalmente diversa. Gli scienziati indiani furono i primi a imboccare lucidamente una via del genere.

Se vi dico che ho già camminato un certo numero di volte sul pianeta Marte e che vi ho incontrato un certo numero di volte Brahmagupta in persona, mi credereste? Probabilmente no. E avreste tutte le ragioni, perché, nella nostra lingua, la frase significa che io ho effettivamente camminato su Marte e che vi ho incontrato Brahmagupta. Tuttavia, in matematica, basta immaginare che quel numero valga zero per capire che non ho mentito. La lingua utilizza strutture differenti a seconda che una cosa sia o non sia. Affermazione: “Ho camminato su Marte.” Negazione: “Non ho camminato su Marte.” La matematica cancella tali differenze e le raggruppa in un’unica e identica formula. “Ho camminato su Marte un certo numero di volte.” Laddove il numero può essere zero.

Se pensate che, pochi secoli prima, i greci avevano sì accettato, ma con fatica, il numero 1, potete immaginare la rivoluzione rappresentata dall’attribuzione della parola “numero” a qualcosa di assente. Prima degli indiani, già alcuni popoli avevano coltivato un pensiero del genere, ma nessuno aveva saputo svilupparlo fino in fondo. I mesopotamici, a partire dal III secolo a.C., erano stati i primi a inventare lo 0. Fino a quel momento, il loro sistema di numerazione scriveva allo stesso modo numeri come 25 e 250. Grazie allo 0, chiamato a indicare un posto vuoto, non era più possibile alcuna confusione. Tuttavia i babilonesi non diedero mai allo 0 lo statuto di numero vero e proprio, e lo scrivevano solo per indicare una completa mancanza di oggetti.

All’altro capo del mondo, anche i maya avevano inventato lo 0. Anzi, ne inventarono addirittura due! Il primo serviva, come quello dei babilonesi, solo per indicare con una cifra, nel loro sistema posizionale basato sul 20, un posto vuoto. Il secondo, invece, era considerato un numero a tutti gli effetti, anche se impiegato solo nell’ambito del calendario. Ogni mese del calendario maya contava venti giorni, numerati da 0 a 19. Lo 0 è impiegato da solo ma svolge una funzione che non si può chiamare matematica. I maya, in altri termini, non se ne servirono mai per effettuare operazioni aritmetiche.

In definitiva, è proprio Brahmagupta il primo ad aver descritto lo zero in quanto numero, accompagnandolo con una descrizione delle sue proprietà: togliendo a un qualunque numero lo stesso numero si ottiene zero; addizionando o sottraendo zero a un numero, il numero resta invariato. Si tratta di proprietà aritmetiche per noi evidenti, ma il fatto che esse siano anche state chiaramente enunciate da Brahmagupta ci dimostra come lo zero sia stato definitivamente integrato come numero, con uno statuto analogo a quello degli altri.

Lo zero apre così la porta ai numeri negativi. Anche se ai matematici occorrerà molto tempo perché li adottino in via definitiva.

I matematici cinesi furono i primi a descrivere quantità riconducibili a numeri negativi. Nei commenti ai Nove capitoli, Liu Hui descrive un sistema di bacchette colorate con le quali si rappresentano quantità positive o negative. Una bacchetta rossa simboleggia un numero positivo, una bacchetta nera simboleggia un numero negativo. E Liu Hui spiega, in dettaglio, come le due specie di numeri interagiscano l’una con l’altra, in particolare come si addizionino o si sottraggano.

La sua descrizione è già molto completa. Gli resta solo da compiere l’ultimo passo: considerare i positivi e i negativi non come due gruppi distinti capaci di interagire, bensì come un unico e identico insieme. È vero che i numeri positivi e negativi non hanno sempre, quando si tratta di fare dei calcoli, le stesse proprietà, ma è altrettanto vero che hanno in primo luogo molti punti in comune che consentono di avvicinarli. È una situazione paragonabile a quella dei numeri pari e dei numeri dispari, i quali formano due gruppi distinti con proprietà aritmetiche diverse ma appartengono in ogni caso alla medesima grande famiglia dei numeri.

Ebbene, una riunificazione del genere, come quella relativa allo zero, saranno gli scienziati indiani a realizzarla per primi. E sarà sempre Brahmagupta a offrirne la disamina completa nel suo Brāhmasphuţasiddhānta. Sulle tracce di Liu Hui, Brahmagupta stabilisce una lista completa delle regole alle quali sono subordinate le operazioni con questi nuovi numeri. Tra l’altro, ci familiarizza con alcuni concetti base. La somma di due numeri negativi è negativa. Esempio: (–3) + (–5) = –8. Il prodotto di un numero positivo e di un numero negativo è negativo. Esempio: (–3) × 8 = –24. Il prodotto di due numeri negativi è positivo. Esempio: (–3) × (–8) = 24. Un concetto, quest’ultimo, che può sembrare controintuitivo e che infatti risulterà uno dei più difficili da accettare. Ancora oggi, esso rappresenta una trappola ben nota, un’insidia temuta dagli studenti del mondo intero.

PERCHÉ MENO PER MENO DÀ PIÙ

Nei secoli che seguiranno l’enunciato di Brahmagupta, le regole di moltiplicazione dei segni, in particolare il “meno × meno = più”, continueranno a suscitare diffidenza e interrogativi.

Interrogativi che trascendono completamente il mondo della matematica e suscitano un notevole livello d’incomprensione quando tali regole vengono insegnate nelle scuole. Nel XIX secolo, persino lo scrittore francese Stendhal esprime la sua incomprensione nel romanzo autobiografico Vita di Henry Brulard. L’autore del Rosso e il Nero e della Certosa di Parma scrive, nel suo romanzo, quanto segue:

“Secondo me, l’ipocrisia era impossibile nella matematica e, nella mia giovanile ingenuità, pensavo che lo stesso avvenisse per tutte le scienze alle quali avevo sentito dire che la matematica si applicava. Rimasi ben male, quando mi accorsi che nessuno poteva spiegarmi perché: meno per meno dà più (– × – = +)! Una delle basi fondamentali della scienza detta algebra.

C’era molto di peggio del non spiegarmi quella difficoltà (senza dubbio spiegabile perché conduce alla verità); mi si davano ragioni evidentemente confuse per coloro che me le esponevano. [...] Mi ridussi a quel che mi dicono ancora oggi: – × – = + deve per forza essere vero, dato che adoperando continuamente questa regola nel calcolo, otteniamo risultati ‘veri e indubitabili’.”11

La regola della moltiplicazione dei segni, certo piuttosto strana al primo approccio, assume tuttavia il suo pieno significato se si ripensa al sistema delle bacchette ideato dagli scienziati cinesi. Proviamo a utilizzare quel sistema per raffigurare guadagni e perdite monetarie. Immaginiamo che una bacchetta nera rappresenti 5 €, e che una bacchetta grigia rappresenti un debito di 5 €, vale a dire: –5 €. Per cui, se possedete 10 bacchette nere e 5 bacchette grigie il vostro saldo equivale a 25 €.

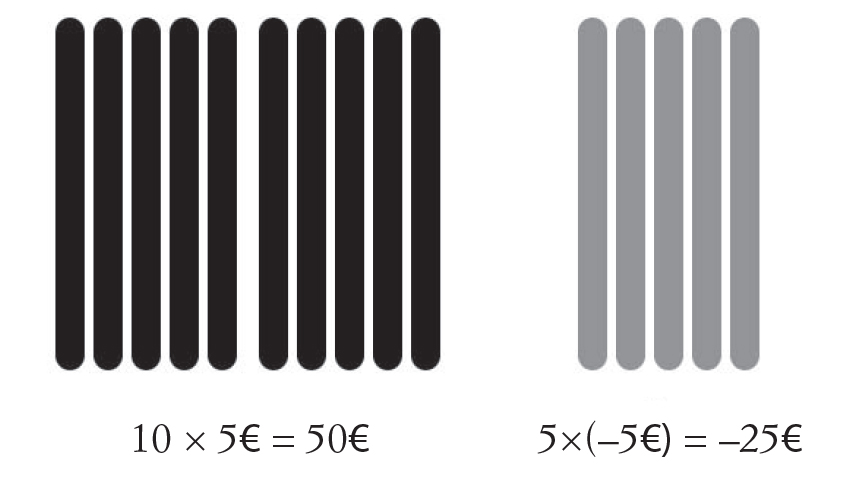
Analizziamo ora i diversi casi di configurazione che possono presentarsi quando il vostro conto subisce una variazione. Immaginate che vi si diano 4 bacchette nere supplementari, nel qual caso il vostro saldo aumenterebbe di 20 €. Detto altrimenti: 4 × 5 = 20. Il prodotto dei due numeri positivi è positivo. E fin qui tutto bene.

Immaginate ora che vi si diano 4 bacchette grigie, vale a dire quattro unità di debito. Nel qual caso il vostro saldo diminuirebbe di 20 €. Detto altrimenti: 4 × (–5) = –20. Un positivo moltiplicato per un negativo dà un negativo. Per cui, se vi si sottraggono 4 bacchette nere, la vostra perdita sarà, in pari misura: –20 €. Il che conferma che (–4) × 5 = – 20. Dove le due ultime situazioni mostrano che il fatto di assegnare delle unità di debito a qualcuno corrisponde a togliergli del denaro. Aggiungere del negativo equivale a sottrarre del positivo.

Ed eccoci al punto cruciale. A quanto ammonta il vostro saldo nel caso vi si sottraessero 4 bacchette grigie? In altri termini, che cosa succederebbe se vi togliessero delle unità di debito? La risposta è chiara: il vostro saldo aumenta, guadagnate denaro. Il che ci porta di nuovo a dire: (– 4) × (– 5) = 20. Togliere del negativo equivale ad aggiungere del positivo! Meno per meno uguale più.

L’avvento dei numeri negativi investirà anche il significato dell’addizione e della sottrazione. Il problema è in tutto e per tutto simile a quello della moltiplicazione per 0,5, vale a dire di una divisione per 2. Se sommare un numero negativo equivale a sottrarre un numero positivo, vuol dire che le due operazioni perdono il significato che hanno nel linguaggio corrente. Sommare è normalmente sinonimo di aumentare. Tuttavia, se sommo il numero –3, non faccio altro che togliere il 3: per esempio, 20 + (–3) = 17. E se, allo stesso modo, sottraggo (–3) non faccio altro che aggiungere il 3: 20 – (–3) = 23. Ancora una volta stiamo semplicemente dando il medesimo nome a cose diverse. Grazie ai numeri negativi, l’addizione e la sottrazione diventano i due volti di un’unica e identica operazione.

La confusione dei termini e la somiglianza con i paradossi, come il “meno × meno = più”, rallenteranno non poco l’adozione dei numeri negativi. Anche molto dopo Brahmagupta, parecchi matematici continueranno a storcere la bocca in presenza di questi numeri terribilmente pratici ma tanto difficili da afferrare. Alcuni li chiameranno “numeri assurdi” e si rassegneranno a utilizzarli nei loro calcoli intermedi a condizione che non compaiano più nel risultato finale. Occorrerà attendere il XIX secolo, o anche il XX, perché la loro legittimità venga pienamente accettata e il loro uso definitivamente adottato.

Nel 711, duemila cavalieri e cammellieri provenienti da Ovest raggiungono la valle dell’Indo. Sono le truppe di Muh.ammad ibn al-Qāsim, giovane condottiero arabo appena ventenne. Meglio equipaggiati e preparati, i suoi soldati annienteranno l’esercito di cinquantamila uomini del ragià Dahir e s’impadroniranno della regione del Sind e del delta del fiume. Per le popolazioni locali si tratta di un evento tragico: migliaia di soldati sono decapitati e la regione è ampiamente saccheggiata.

Il formarsi di un giovanissimo impero arabo-musulmano alle porte dell’India sarà, nonostante tutto, una fortuna per la diffusione della matematica indiana. Immediatamente, i sapienti arabi integreranno le proprie scoperte con quelle degli scienziati indiani e daranno loro una risonanza mondiale, la cui eco si spande ancora sulla matematica del XXI secolo.

11 Stendhal, Vita di Henry Brulard, trad. it. di M. Zini, Einaudi, Torino 1976, p. 281. (N.d.T.)