Kinematics is the study of an object’s motion in terms of its displacement, velocity, and acceleration. Questions such as, How far does this object travel? Or, How fast and in what direction does it move? Or, At what rate does its speed change? All properly belong to kinematics. In the next chapter, we will study dynamics, which delves more deeply into why objects move the way they do.
Any object exists in some location somewhere in the universe. We call that location the object’s position, but the position is meaningless without some reference point. We can arbitrarily choose one location and call it the origin. Many times it makes sense to let the object in question start at the origin, but this is not required and the laws of physics work no matter where you place the origin or whether you choose to make the up-direction positive and down-direction negative or vice versa. As we go more in depth in the problem-solving sections, you will notice that the mathematics sometimes simplifies greatly with a cleverly chosen coordinate system and origin.

Displacement is an object’s change in position. It’s the vector that points from the object’s initial position to its final position, regardless of the path actually taken. Since displacement means change in position, it is generically denoted ∆s, where ∆ denotes change in and s means spatial location. (The letter p is not used for position because it’s reserved for another quantity called momentum. We’ll discuss momentum in Chapter 5.) If it’s known that the displacement is horizontal, then it can be called ∆x; if the displacement is vertical, then it’s ∆y. The magnitude of this vector is the net distance traveled and, sometimes, the word displacement refers just to this scalar quantity. Since a distance is being measured, the SI unit for displacement is the meter [∆s] = m.
Example 2.1 A rock is thrown straight upward from the edge of a 30 m cliff, rising 10 m then falling all the way down to the base of the cliff. Find the rock’s displacement.
Solution. Displacement only refers to the object’s initial position and final position, not the details of its journey. Since the rock started on the edge of the cliff and ended up on the ground 30 m below, its displacement is 30 m, downward.
Example 2.2 An infant crawls 5 m east, then 3 m north, then 1 m east. Find the magnitude of the infant’s displacement.
Solution. Although the infant crawled a total distance of 5 + 3 + 1 = 9 m, this is not the displacement, which is merely the net distance traveled.
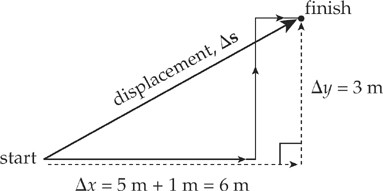
Using the Pythagorean theorem, we can calculate that the magnitude of the displacement is
Example 2.3 In a track-and-field event, an athlete runs exactly once around an oval track, a total distance of 500 m. Find the runner’s displacement for the race.
Solution. If the runner returns to the same position from which she left, then her displacement is zero.

The total distance covered is 500 m, but the net distance—the displacement—is 0.
∆s is a more general term that works in space. The term x or “∆x = xf – xi” has a specific meaning that is defined in the x direction. However to be consistent with AP notation, and to avoid confusion between spacial location and speed, from this point on we will use x in our development of the concepts of speed, velocity, and acceleration. It should be noted that the concepts developed work equally well in the y direction.
When we’re in a moving car, the speedometer tells us how fast we’re going; it gives us our speed. But what does it mean to have a speed of say, 10 m/s? It means that we’re covering a distance of 10 meters every second. By definition, average speed is the ratio of the total distance traveled to the time required to cover that distance:
The car’s speedometer doesn’t care in what direction the car is moving (as long as the wheels are moving forward). You could be driving north, south, east, west, whatever; the speedometer would make no distinction. 55 miles per hour, north and 55 miles per hour, east register the same on the speedometer: 55 miles per hour. Speed is a scalar.
However, we will also need to include direction in our descriptions of motion. We just learned about displacement, which takes both distance (net distance) and direction into account. The single concept that embodies both speed and direction is called velocity, and the definition of average velocity is:
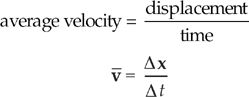
(The bar over the v means average.) Because ∆x is a vector, ![]() is also a vector, and because ∆t is a positive scalar, the direction of
is also a vector, and because ∆t is a positive scalar, the direction of ![]() is the same as the direction of ∆x. The magnitude of the velocity vector is called the object’s speed, and is expressed in units of meters per second (m/s).
is the same as the direction of ∆x. The magnitude of the velocity vector is called the object’s speed, and is expressed in units of meters per second (m/s).
Note the distinction between speed and velocity. In everyday language, they’re often used interchangeably. However, in physics, speed and velocity are technical terms whose definitions are not the same. Velocity is speed plus direction. An important note: The magnitude of the velocity is the speed. However (and this is perhaps a bit unfortunate and can be confusing), the magnitude of the average velocity is not called the average speed. Average speed is defined as the total distance traveled divided by the elapsed time. On the other hand, the magnitude of the average velocity is the net distance traveled divided by the elapsed time.
Example 2.4 If the infant in Example 2.2 completes his journey in 20 seconds, find the magnitude of his average velocity.
Solution. Since the displacement is 6.7 m, the magnitude of his average velocity is
Example 2.5 Assume that the runner in Example 2.3 completes the race in 1 minute and 18 seconds. Find her average speed and the magnitude of her average velocity.
Solution. Average speed is total distance divided by elapsed time. Since the length of the track is 500 m, the runner’s average speed was (500 m) / (78 s) = 6.4 m/s. However, since her displacement was zero, her average velocity was zero also: ![]() = ∆x/∆t = (0 m) / (78 s) = 0 m/s.
= ∆x/∆t = (0 m) / (78 s) = 0 m/s.
Example 2.6 Is it possible to move with constant speed but not constant velocity? Is it possible to move with constant velocity but not constant speed?
Solution. The answer to the first question is yes. For example, if you set your car’s cruise control at 55 miles per hour but turn the steering wheel to follow a curved section of road, then the direction of your velocity changes (which means your velocity is not constant), even though your speed doesn’t change.
The answer to the second question is no. Velocity means speed and direction; if the velocity is constant, then that means both speed and direction are constant. If speed were to change, then the velocity vector’s magnitude would change (by definition), which immediately implies that the vector changes.
When you step on the gas pedal in your car, the car’s speed increases; step on the brake and the car’s speed decreases. Turn the wheel, and the car’s direction of motion changes. In all of these cases, the velocity changes. To describe this change in velocity, we need a new term: acceleration. In the same way that velocity measures the rate-of-change of an object’s position, acceleration measures the rate-of-change of an object’s velocity. An object’s average acceleration is defined as follows:
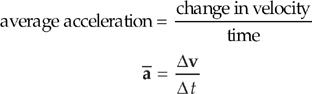
The units of acceleration are meters per second, per second: [a] = m/s2. Because ∆v is a vector, ā is also a vector; and because ∆t is a positive scalar, the direction of ā is the same as the direction of ∆v.
Furthermore, if we take an object’s original direction of motion to be positive, then an increase in speed corresponds to a positive acceleration, while a decrease in speed corresponds to a negative acceleration (deceleration). However, if an object’s original direction is negative, then an increase in speed corresponds to a negative acceleration, while a decrease in speed corresponds to a positive acceleration. So, when the velocity and acceleration are in the same direction (they have the same sign), the object speeds up. When the velocity and acceleration are in the opposite direction (one is negative and one is positive, no matter which is which) the object slows down.
Note that an object can accelerate even if its speed doesn’t change. (Again, it’s a matter of not allowing the everyday usage of the word accelerate to interfere with its technical, physics usage.) This is because acceleration depends on ∆v, and the velocity vector v changes if (1) speed changes, or (2) direction changes, or (3) both speed and direction change. For instance, a car traveling around a circular racetrack is constantly accelerating even if the car’s speed is constant, because the direction of the car’s velocity vector is constantly changing.
Example 2.7 A car is traveling in a straight line along a highway at a constant speed of 80 miles per hour for 10 seconds. Find its acceleration.
Solution. Since the car is traveling at a constant velocity, its acceleration is zero. If there’s no change in velocity, then there’s no acceleration.
Example 2.8 A car is traveling along a straight highway at a speed of 20 m/s. The driver steps on the gas pedal and, 3 seconds later, the car’s speed is 32 m/s. Find its average acceleration.
Solution. Assuming that the direction of the velocity doesn’t change, it’s simply a matter of dividing the change in velocity, 32 m/s – 20 m/s = 12 m/s, by the time interval during which the change occurred: ā = ∆v/∆t = (12 m/s) / (3 s) = 4 m/s2.
Example 2.9 Spotting a police car ahead, the driver of the car in the previous example slows from 32 m/s to 20 m/s in 2 seconds. Find the car’s average acceleration.
Solution. Dividing the change in velocity, 20 m/s – 32 m/s = –12 m/s, by the time interval during which the change occurred, 2 s, give us ā = ∆v/∆t = (–12 m/s) / (2 s) = –6 m/s2. The negative sign here means that the direction of the acceleration is opposite the direction of the velocity, which describes slowing down.
The simplest type of motion to analyze is motion in which the acceleration is constant (possibly equal to zero). Although true uniform acceleration is rarely achieved in the real world, many common motions are governed by approximately constant acceleration and, in these cases, the kinematics of uniformly accelerated motion provide a pretty good description of what’s happening. Notice that if the acceleration is constant, then taking an average yields nothing new, so ā = a.
Another restriction that will make our analysis easier is to consider only motion that takes place along a straight line. In these cases, there are only two possible directions of motion. One is positive, and the opposite direction is negative. Most of the quantities we’ve been dealing with—displacement, velocity, and acceleration—are vectors, which means that they include both a magnitude and a direction. With straight-line motion, direction can be specified simply by attaching a + or – sign to the magnitude of the quantity. Therefore, although we will often abandon the use of bold letters to denote the vector quantities of displacement, velocity, and acceleration, the fact that these quantities include direction will still be indicated by a positive or negative sign.
Let’s review the quantities we’ve seen so far. The fundamental quantities are position (x), velocity (v), and acceleration (a). Acceleration is a change in velocity, from an initial velocity (vi or v0) to a final velocity (vf or simply v—with no subscript). And, finally, the motion takes place during some elapsed time interval, ∆t. Also, if we agree to start our clocks at time ti = 0, then ∆t = tf – ti = t – 0 = t, so we can just write t instead of ∆t in the first four equations. This simplification in notation makes these equations a little easier to write down. Therefore, we have five kinematics quantities: ∆x, v0, v, a, and ∆t.
These five quantities are related by a group of five equations that we call the Big Five. They work in cases where acceleration is uniform, which are the cases we’re considering.

Each of the Big Five equations is missing one of the five kinematic quantities. The way you decide which equation to use when solving a problem is to determine which of the kinematic quantities is missing from the problem—that is, which quantity is neither given nor asked for—and then use the equation that doesn’t contain that variable. For example, if the problem never mentions the final velocity—v is neither given nor asked for—the equation that will work is the one that’s missing v. That’s Big Five #3.
Big Five #1 and #2 are simply the definitions of ![]() and ā written in forms that don’t involve fractions. The other Big Five equations can be derived from these two definitions and the equation
and ā written in forms that don’t involve fractions. The other Big Five equations can be derived from these two definitions and the equation ![]() , using a bit of algebra.
, using a bit of algebra.
Example 2.10 An object with an initial velocity of 4 m/s moves along a straight axis under constant acceleration. Three seconds later, its velocity is 14 m/s. How far did it travel during this time?
Solution. We’re given v0, ∆t, and v, and we’re asked for x. So a is missing; it isn’t given and it isn’t asked for, and we use Big Five #1:
Note: This last equation could also have been written as
That is, it’s okay to leave off the units in the middle of the calculation as long as you remember to include them in your final answer. Leaving units off of your final answer will cost you points on the AP exam.
Example 2.11 A car that’s initially traveling at 10 m/s accelerates uniformly for 4 seconds at a rate of 2 m/s2, in a straight line. How far does the car travel during this time?
Solution. We’re given v0, t, and a, and we’re asked for x. So, v is missing; it isn’t given and it isn’t asked for, and we use Big Five #3:
Example 2.12 A rock is dropped off a cliff that’s 80 m high. If it strikes the ground with an impact velocity of 40 m/s, what acceleration did it experience during its descent?
Solution. If something is dropped, then that means it has no initial velocity: v0 = 0. So, we’re given v0, ∆x, and v, and we’re asked for a. Since t is missing, we use Big Five #5:
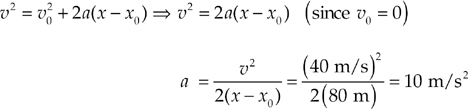
Note that since a has the same sign as (x – x0), the acceleration vector points in the same direction as the displacement vector. This makes sense here, since the object moves downward and the acceleration it experiences is due to gravity, which also points downward.
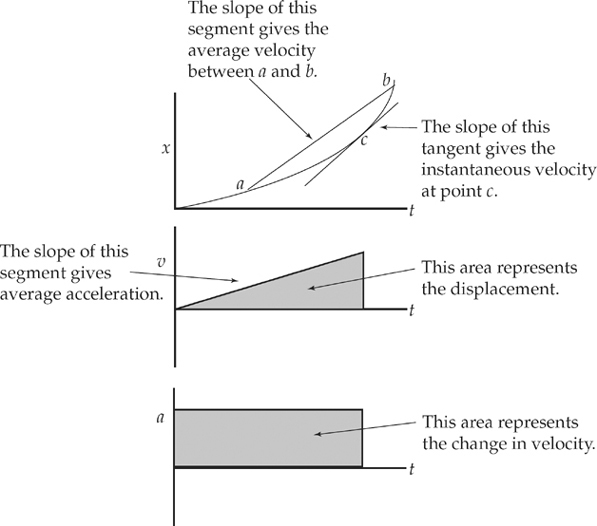
So far, we have dealt with kinematics problems algebraically, but you should also be able to handle kinematics questions in which information is given graphically. The two most popular graphs in kinematics are position-vs.-time graphs and velocity-vs.-time graphs. For example, consider an object that’s moving along an axis in such a way that its position x as a function of time t is given by the following position-vs.-time graph:
What does this graph tell us? It says that at time t = 0, the object was at position x = 0. Then, in the first second, its position changed from x = 0 to x = 10 m. Then, at time t = 1 s to 3 s it stopped. From t = 3 s to t = 6 s, it reversed direction, reaching x = 0 at time t = 5 s, and continued, reaching position x = –5 m at time t = 6 s. Notice how economically the graph embodies all this information!
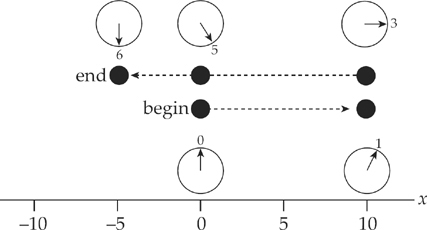
We can also determine the object’s average velocity (and average speed) during particular time intervals. For example, its average velocity from time t = 0 to time t = 1 s is equal to the object’s displacement, 10 – 0 = 10 m, divided by the elapsed time, 2 s:

Note, however, that the ratio that defines the average velocity, ∆x/∆t, also defines the slope of the x vs. t graph. Therefore, we know the following important fact:
What was the average velocity from time t = 3 s to time t = 6 s? The slope of the line segment joining the point (t, x) = (3 s, 10 m) to the point (t, x) = (6 s, – 5m) is
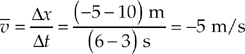
The fact that ![]() is negative tells us that the object’s displacement was negative during this time interval; that is, it moved in the negative x direction. The fact that
is negative tells us that the object’s displacement was negative during this time interval; that is, it moved in the negative x direction. The fact that ![]() is negative agrees with the observation that the slope of a line that falls to the right is negative. What is the object’s average velocity from time t = 1 s to time t = 3 s? Since the line segment from t = 1 s to t = 3 s is horizontal, its slope is zero, which implies that the average velocity is zero, but we can also figure this out from looking at the graph, since the object’s position did not change during that time.
is negative agrees with the observation that the slope of a line that falls to the right is negative. What is the object’s average velocity from time t = 1 s to time t = 3 s? Since the line segment from t = 1 s to t = 3 s is horizontal, its slope is zero, which implies that the average velocity is zero, but we can also figure this out from looking at the graph, since the object’s position did not change during that time.
Finally, let’s figure out the object’s average velocity and average speed for its entire journey (from t = 0 to t = 6 s). The average velocity is
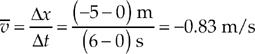
This is the slope of the imagined line segment that joins the point (t, x) = (0 s, 0 m) to the point (t, x) = (6 s, –5 m). The average speed is the total distance traveled by the object divided by the elapsed time. In this case, notice that the object traveled 10 m in the first 1 s, then 15 m (albeit backwards) in the next 3 s. It covered no additional distance from t = 1 s to t = 3 s. Therefore, the total distance traveled by the object is d = 10 + 15 = 25 m, which took 6 s, so
Not all graphs have nice straight lines as shown so far. Straight line segments represent constant slopes and therefore constant velocities. What happens as an object changes its velocity? The “lines” become “curves.” Let’s look at a typical question that might be asked about such a curve.
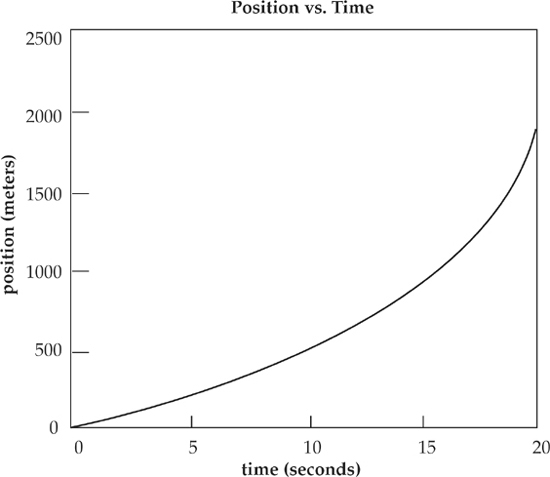
a) What is the average velocity from 0 to 10 seconds?
b) What is the average velocity from 10 to 20 seconds?
c) What is the average velocity from 0 to 20 seconds?
Solution. This is familiar territory. To find the average velocity use
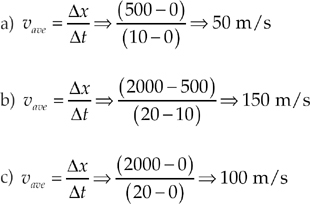
The instantaneous velocity is the velocity at a given moment in time. When you drive in a car and look down at the speedometer, you see your instantaneous velocity at that time. To find the true instantaneous velocity from a position-vs.-time graph you need some calculus. However, we can get a very good approximation by finding the position a very small amount of time before the time in question and the position a very small time after the time in question.
For example, what if you wish to find the instantaneous velocity at 10 seconds? The velocity from 9–10 seconds is close to the velocity at 10 seconds, but it is still a bit too slow. The velocity from 10–11 seconds is also close to the velocity at 10 seconds, but it is still a bit too fast. You can find the middle ground between these two ideas, or the slope of the line that connects the point before and the point after 10 seconds. This is very close to the instantaneous velocity. A true tangent line touches the curve at only one point, but this line is close enough for our purposes.
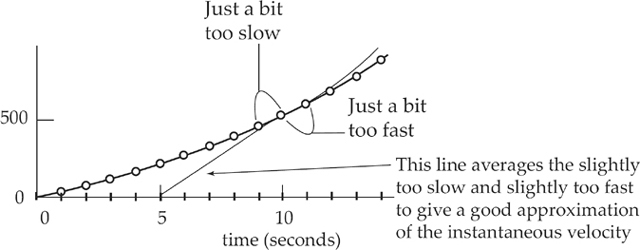
Solution. Draw a tangent line. Find the slope of the tangent by picking any two points on the tangent line. It usually helps if the points are kind of far apart and it also helps if points can be found at “easy spots” such as (0, 5) and (15, 1000) and not (6.27, 113) and (14.7, 983)
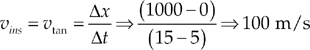
Let’s look at three handy shortcuts for objects that start from rest and have a constant acceleration:
Please note: Shortcuts 2 and 3 are true only for objects that start from rest and have a constant acceleration.
Let’s next consider an object moving along a straight axis in such a way that its velocity, v, as a function of time, t, is given by the following velocity-vs.-time graph:

What does this graph tell us? It says that, at time t = 0, the object’s velocity was v = 0. Over the first two seconds, its velocity increased steadily to 10 m/s. At time t = 2 s, the velocity then began to decrease (eventually becoming v = 0, at time t = 3 s). The velocity then became negative after t = 3 s, reaching v = –5 m/s at time t = 3.5 s. From t = 3.5 s on, the velocity remained a steady –5 m/s.
What can we ask about this motion? First, the fact that the velocity changed from t = 0 to t = 2 s tells us that the object accelerated. The acceleration during this tme was

Note, however, that the ratio that defines the acceleration, ∆v/∆t, also defines the slope of the v vs. t graph. Therefore,
What was the acceleration from time t = 2 s to time t = 3.5 s? The slope of the line segment joining the point (t, v) = (2 s, 10 m/s) to the point (t, v) = (3.5 s, –5 m/s) is
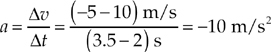
The fact that a is negative tells us that the object’s velocity change was negative during this time interval; that is, the object accelerated in the negative direction. In fact, after time t = 3 s, the velocity became more negative, indicating that the direction of motion was negative at increasing speed. What is the object’s acceleration from time t = 3.5 s to time t = 6 s? Since the line segment from t = 3.5 s to t = 6 s is horizontal, its slope is zero, which implies that the acceleration is zero, but you can also see this from looking at the graph; the object’s velocity did not change during this time interval.
Another question can be asked when a velocity-vs.-time graph is given: How far did the object travel during a particular time interval? For example, let’s figure out the displacement of the object from time t = 4 s to time t = 6 s. During this time interval, the velocity was a constant –5 m/s, so the displacement was ∆x = v∆t = (–5 m/s)(2 s) = –10 m.
Geometrically, we’ve determined the area between the graph and the horizontal axis. After all, the area of a rectangle is base × height and, for the shaded rectangle shown below, the base is ∆t, and the height is v. So, base × height equals ∆t × v, which is displacement.
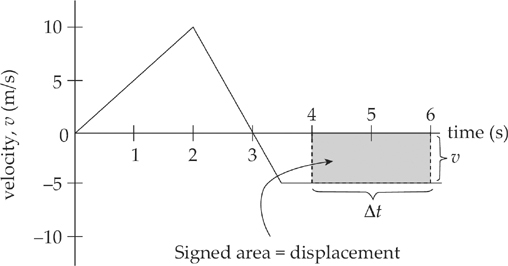
We say signed area because regions below the horizontal axis are negative quantities (since the object’s velocity is negative, its displacement is negative). Therefore, counting areas above the horizontal axis as positive and areas below the horizontal axis as negative, we can make the following claim:
Given a velocity-vs.-time graph, the area between the graph and the t axis equals the object’s displacement.
What is the object’s displacement from time t = 0 to t = 3 s? Using the fact that displacement is the area bounded by the velocity graph, we figure out the area of the triangle shown below:
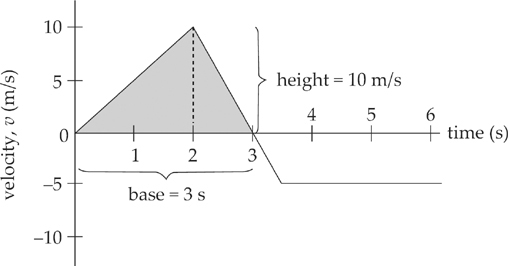
Since the area of a triangle is ![]() × base × height, we find that Δx =
× base × height, we find that Δx = ![]() (3 s)(10 m/s) = 15 m.
(3 s)(10 m/s) = 15 m.
Beyond all the math, you are at a clear advantage when you start to recognize that position-vs.-time and velocity-vs.-time graphs have a few basic shapes, and that all the graphs you will see will be some form of these basic shapes. Having a feel for these building blocks will go a long way toward understanding kinematics graphs in physics.
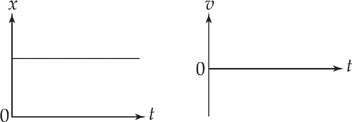
Either of the following two graphs represents something that is not moving.
Either of the following two graphs represents an object moving at a constant velocity in the positive direction.

Either of the following two graphs represents an object moving at a constant velocity in the negative direction.

Either of the following two graphs represents an object speeding up in the positive direction.
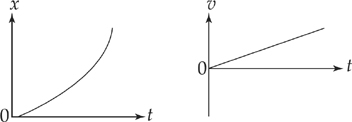
Either of the following two graphs represents an object slowing down in the positive direction.

Either of the following two graphs represents an object slowing down in the negative direction.
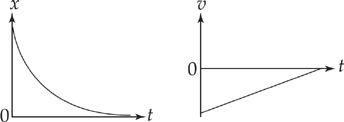
Either of the following two graphs represents an object speeding up in the negative direction.

Example 2.15 Here is a position-vs.-time graph. Describe in words the motion of the object and sketch the corresponding velocity-vs.-time graph.
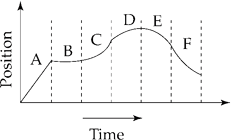
Solution. Part A is a constant speed moving away from the origin, part B is at rest, part C is speeding up moving away from the origin, part D is slowing down still moving away from the origin, part E is speeding up moving back toward the origin, and part F is slowing down moving back toward the origin
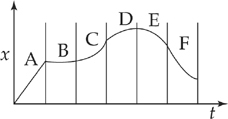
Example 2.16 The velocity of an object as a function of time is given by the following graph:
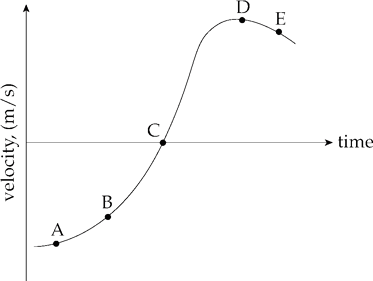
At which point (A, B, C, D, or E) is the magnitude of the acceleration the greatest? How would you answer this same question if the graph shown were a position-vs.-time graph?
Solution. The acceleration is the slope of the velocity-vs.-time graph. Although this graph is not composed of straight lines, the concept of slope still applies; at each point, the slope of the curve is the slope of the tangent line to the curve. The slope is essentially zero at Points A and D (where the curve is flat), small and positive at B, and small and negative at E. The slope at Point C is large and positive, so this is where the object’s acceleration is the greatest.
If the graph shown were a position-vs.-time graph, then the slope would be the velocity. The slope of the given graph starts at zero (around Point A), slowly increases to a small positive value at B, continues to slowly increase to a large positive value at C, then, at around Point D, this large positive slope decreases quickly to zero. Of the points designated on the graph, Point D is the location of the greatest slope change, which means that this is the point of the greatest velocity change. Therefore, this is the point at which the magnitude of the acceleration is greatest.
The simplest real-life example of motion under pretty constant acceleration is the motion of objects in the earth’s gravitational field, near the surface of the earth and ignoring any effects due to the air (mainly air resistance). With these effects ignored, an object can fall freely, that is, it can fall experiencing only acceleration due to gravity. Near the surface of the earth, the gravitational acceleration has a constant magnitude of about 9.8 m/s2; this quantity is denoted g (for gravitational acceleration). On the AP Physics Exam, you may use g = 10 m/s2 as a simple approximation to g = 9.8 m/s2. This is particularly helpful because, as we mentioned earlier, you will not be permitted to use a calculator on the multiple-choice section. In this book, we will always use g = 10 m/s2. And, of course, the gravitational acceleration vector, g, points downward.
Although you are allowed to choose any coordinate system you wish, most students will increase their degree of success by sticking with the convention that up is positive and down is negative. Typically, we will use that convention here as well. Gravity points down, so we will use g = –10 m/s2.
In each of the following examples, we’ll ignore effects due to the air.
Example 2.17 A rock is dropped from a cliff 80 m above the ground. How long does it take to reach the ground?
Solution. We are given vo, and asked for t. Unless you specifically see words to the contrary (such as, “you are on the moon where the acceleration due to gravity is.…”) assume you are also given a = –10m/s2. Because v is missing, and it isn’t asked for, we can use Big Five equation #3.
If we set the origin y0 = 0 at the base of the cliff and v0 = 0, we get:
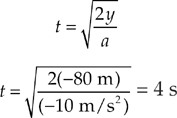
Note: The negative in front of the 80 is inserted because the rock fell in the down direction.
Example 2.18 A baseball is thrown straight upward with an initial speed of 20 m/s. How high will it go?
Solution. We are given v0, a = –10 m/s2 is implied, and we are asked for y. Now, neither t nor v is expressly given; however, we know the vertical velocity at the top is 0 (otherwise the baseball would still rise). Consequently, we use Big Five equation #5.
We set y0 = 0 and we know that v = 0, so that leaves us with:
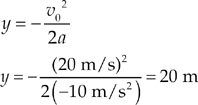
Example 2.19 One second after being thrown straight down, an object is falling with a speed of 20 m/s. How fast will it be falling 2 seconds later?
Solution. We’re given v0, a, and t, and asked for v. Since x is missing, we use Big Five #2:
The negative sign in front of the 40 simply indicates that the object is traveling in the down direction.
Example 2.20 If an object is thrown straight upward with an initial speed of 8 m/s and takes 3 seconds to strike the ground, from what height was the object thrown?
Solution. We’re given a, v0, and t, and we need to find y0. Because v is missing, we use Big Five #3:

In general, an object that moves near the surface of the earth will not follow a straight-line path (for example, a baseball hit by a bat, a golf ball struck by a club, or a tennis ball hit from the baseline). If we launch an object at an angle other than straight upward and consider only the effect of acceleration due to gravity, then the object will travel along a parabolic trajectory.

To simplify the analysis of parabolic motion, we analyze the horizontal and vertical motions separately, using the Big Five. This is the key to doing projectile motion problems. Calling down the negative direction, we have

The quantity v0x, which is the horizontal (or x) component of the initial velocity, is equal to v0 cos θ0, where θ0 is the launch angle, the angle that the initial velocity vector, v0, makes with the horizontal. Similarly, the quantity v0y, the vertical (or y) component of the initial velocity, is equal to v0 sin θ0.
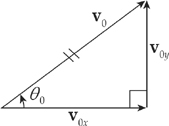
Example 2.21 An object is thrown horizontally with an initial speed of 10 m/s. It hits the ground 4 seconds later. How far did it drop in 4 seconds?
Solution. The first step is to decide whether this is a horizontal question or a vertical question, since you must consider these motions separately. The question How far will it drop? is a vertical question, so the set of equations we will consider are those listed above under vertical motion. Next, How far …? implies that we will use the first of the vertical-motion equations, the one that gives vertical displacement, ∆y.
Now, since the object is thrown horizontally, there is no vertical component to its initial velocity vector v0; that is, v0y = 0. Therefore,
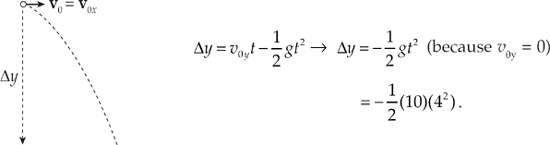
The fact that ∆y is negative means that the displacement is down. Also, notice that the information given about v0x is irrelevant to the question.
Example 2.22 From a height of 100 m, a ball is thrown horizontally with an initial speed of 15 m/s. How far does it travel horizontally in the first 2 seconds?
Solution. The question, How far does it travel horizontally …?, immediately tells us that we should use the first of the horizontal-motion equations listed above:
The information that the initial vertical position is 100 m above the ground is irrelevant (except for the fact that it’s high enough that the ball doesn’t strike the ground before the two seconds have elapsed).
Example 2.23 A projectile is traveling in a parabolic path for a total of 6 seconds. How does its horizontal velocity 1 s after launch compare to its horizontal velocity 4 s after launch?
Solution. The only acceleration experienced by the projectile is due to gravity, which is purely vertical, so that there is no horizontal acceleration. If there’s no horizontal acceleration, then the horizontal velocity cannot change during flight, and the projectile’s horizontal velocity 1 s after it’s launched is the same as its horizontal velocity 3 s later.
Example 2.24 An object is projected upward with a 30° launch angle and an initial speed of 40 m/s. How long will it take for the object to reach the top of its trajectory? How high is this?
Solution. When the projectile reaches the top of its trajectory, its velocity vector is momentarily horizontal; that is, vy = 0. Using the vertical-motion equation for vy, we can set it equal to 0 and solve for t:
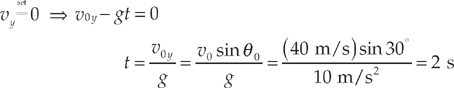
At this time, the projectile’s vertical displacement is
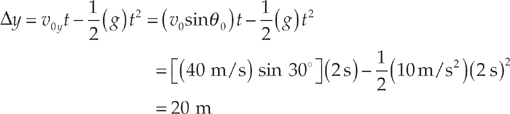
Example 2.25 An object is projected upward with a 30° launch angle from the ground and an initial speed of 60 m/s. For how many seconds will it be in the air? How far will it travel horizontally? Assume it returns to its original height.
Solution. The total time the object spends in the air is equal to twice the time required to reach the top of the trajectory (because the parabola is symmetrical). So, as we did in the previous example, we find the time required to reach the top by setting vy equal to 0, and now double that amount of time:

Therefore, the total flight time (that is, up and down) is tt = 2t = 2 × (3 s) = 6 s.
Now, using the first horizontal-motion equation, we can calculate the horizontal displacement after 6 seconds:
By the way, assuming it lands back at its original height, the full horizontal displacement of a projectile is called the projectile’s range.
Solutions can be found in Chapter 18.
1. An object that’s moving with constant speed travels once around a circular path. Which of the following is/are true concerning this motion?
I. The displacement is zero.
II. The average speed is zero.
III. The acceleration is zero.
(A) I only
(B) I and II only
(C) I and III only
(D) III only
(E) II and III only

In section 5 of the velocity-time graph the object is
(A) speeding up moving in the positive direction
(B) slowing down moving in the positive direction
(C) speeding up moving in the negative direction
(D) slowing down moving in the negative direction
(E) this can not be determined without the position-time graph
3. Which of the following is/are true?
I. If an object’s acceleration is constant, then it must move in a straight line.
II. If an object’s acceleration is zero, then its speed must remain constant.
III. If an object’s speed remains constant, then its acceleration must be zero.
(A) I and II only
(B) I and III only
(C) II only
(D) III only
(E) II and III only
4. A baseball is thrown straight upward. What is the ball’s acceleration at its highest point?
(A) 0
(B) ![]() g, downward
g, downward
(C) g, downward
(D) ![]() g, upward
g, upward
(E) g, upward
5. How long would it take a car, starting from rest and accelerating uniformly in a straight line at 5 m/s2, to cover a distance of 200 m?
(A) 9.0 s
(B) 10.5 s
(C) 12.0 s
(D) 15.5 s
(E) 20.0 s
6. A rock is dropped off a cliff and strikes the ground with an impact velocity of 30 m/s. How high was the cliff?
(A) 15 m
(B) 20 m
(C) 30 m
(D) 45 m
(E) 60 m
7. A stone is thrown horizontally with an initial speed of 10 m/s from a bridge. If air resistance could be ignored, how long would it take the stone to strike the water 80 m below the bridge?
(A) 1 s
(B) 2 s
(C) 4 s
(D) 6 s
(E) 8 s
8. A soccer ball, at rest on the ground, is kicked with an initial velocity of 10 m/s at a launch angle of 30°. Calculate its total flight time, assuming that air resistance is negligible.
(A) 0.5 s
(B) 1 s
(C) 1.7 s
(D) 2 s
(E) 4 s
9. A stone is thrown horizontally with an initial speed of 30 m/s from a bridge. Find the stone’s total speed when it enters the water 4 seconds later. (Ignore air resistance.)
(A) 30 m/s
(B) 40 m/s
(C) 50 m/s
(D) 60 m/s
(E) 70 m/s
10. Which one of the following statements is true concerning the motion of an ideal projectile launched at an angle of 45° to the horizontal?
(A) The acceleration vector points opposite to the velocity vector on the way up and in the same direction as the velocity vector on the way down.
(B) The speed at the top of the trajectory is zero.
(C) The object’s total speed remains constant during the entire flight.
(D) The horizontal speed decreases on the way up and increases on the way down.
(E) The vertical speed decreases on the way up and increases on the way down.
1. This question concerns the motion of a car on a straight track; the car’s velocity as a function of time is plotted below.
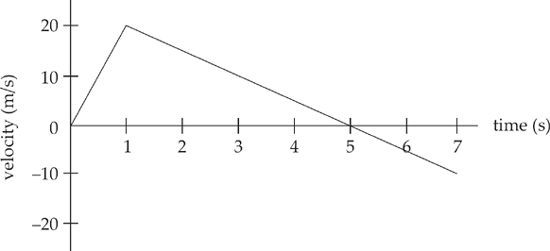
(a) Describe what happened to the car at time t = 1 s.
(b) How does the car’s average velocity between time t = 0 and t = 1 s compare to its average velocity between times t = 1 s and t = 5 s?
(c) What is the displacement of the car from time t = 0 to time t = 7 s?
(d) Plot the car’s acceleration during this interval as a function of time.
(e) Make a sketch of the object’s position during this interval as a function of time. Assume that the car begins at x = 0.
2. Consider a projectile moving in a parabolic trajectory under constant gravitational acceleration. Its initial velocity has magnitude v0, and its launch angle (with the horizontal) is θ0.
(a) Calculate the maximum height, H, of the projectile.
(b) Calculate the (horizontal) range, R, of the projectile.
(c) For what value of θ0 will the range be maximized?
(d) If 0 < h < H, compute the time that elapses between passing through the horizontal line of height h in both directions (ascending and descending); that is, compute the time required for the projectile to pass through the two points shown in this figure:

3. A cannonball is shot with an initial speed of 50 m/s at a launch angle of 40° toward a castle wall 220 m away. The height of the wall is 30 m. Assume that effects due to the air are negligible. (For this problem, use g = 9.8 m/s2.)
(a) Show that the cannonball will strike the castle wall.
(b) How long will it take for the cannonball to strike the wall?
(c) At what height above the base of the wall will the cannonball strike?
Graphs are very useful tools to help visualize the motion of an object. They can also help you solve problems once you learn how to translate from one graph to another. As you work with graphs, keep the following things in mind:

* Because the acceleration is uniform, this may also be written as Δx = ![]() (v0 + v)t.
(v0 + v)t.
** Historically, these three equations have been given on the AP Physics B equation sheet for the free-response section. Again, no equations are provided for the multiple-choice section.

At any given moment the relationship between v, vx, and vy is given by
