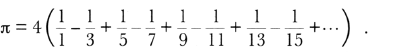
‘Do you know,’ the Devil confided, ‘not even the best mathematicians on other planets – all far ahead of yours – have solved it? Why, there’s a chap on Saturn – he looks something like a mushroom on stilts – who solves partial differential equations mentally; and even he’s given up.’
Arthur Porges, ‘The Devil and Simon Flagg’
Pierre de Fermat was born on 20 August 1601 in the town of Beaumont-de-Lomagne in south-west France. Fermat’s father, Dominique Fermat, was a wealthy leather merchant, and so Pierre was fortunate enough to enjoy a privileged education at the Franciscan monastery of Grandselve, followed by a stint at the University of Toulouse. There is no record of the young Fermat showing any particular brilliance in mathematics.
Pressure from his family steered Fermat towards a career in the civil service, and in 1631 he was appointed conseiller au Parlement de Toulouse, a councillor at the Chamber of Petitions. If locals wanted to petition the King on any matter they first had to convince Fermat or one of his associates of the importance of their request. The councillors provided the vital link between the province and Paris. As well as liaising between the locals and the monarch, the councillors made sure that royal decrees emanating from the capital were implemented back in the regions. Fermat was an efficient civil servant, who by all accounts carried out his duties in a considerate and merciful manner.
Fermat’s additional duties included service in the judiciary and he was senior enough to deal with the most severe cases. An account of his work is given by the English mathematician, Sir Kenelm Digby. Digby had requested to see Fermat, but in a letter to a mutual colleague, John Wallis, he reveals that the Frenchman had been occupied with pressing judicial matters, thus excluding the possibility of a meeting:
It is true that I had exactly hit the date of the displacement of the judges of Castres to Toulouse, where he [Fermat] is the Supreme Judge to the Sovereign Court of Parliament; and since then he has been occupied with capital cases of great importance, in which he has finished by imposing a sentence that has made a great stir; it concerned the condemnation of a priest, who had abused his functions, to be burned at the stake. This affair has just finished and the execution has followed.
Fermat corresponded regularly with Digby and Wallis. Later we will see that the letters were often less than friendly, but they provide vital insights into Fermat’s daily life, including his academic work.
Fermat rose rapidly within the ranks of the civil service and became a member of the social élite, entitling him to use de as part of his name. His promotion was not necessarily the result of ambition, but rather a matter of health. The plague was raging throughout Europe and those who survived were elevated to fill the places of those who died. Even Fermat suffered a serious bout of plague in 1652, and was so ill that his friend Bernard Medon announced his death to several colleagues. Soon after he corrected himself in a report to the Dutchman Nicholas Heinsius:
I informed you earlier of the death of Fermat. He is still alive, and we no longer fear for his health, even though we had counted him among the dead a short time ago. The plague no longer rages among us.
In addition to the health risks of seventeenth-century France, Fermat had to survive the political dangers. His appointment to the Parliament of Toulouse came just three years after Cardinal Richelieu was promoted to first minister of France. This was an era of plotting and intrigue, and everyone involved in the running of the state, even at local government level, had to take care not to become embroiled in the machinations of the Cardinal. Fermat adopted the strategy of performing duties efficiently without drawing attention to himself. He had no great political ambition, and did his best to avoid the rough and tumble of parliament. Instead he devoted all his spare energy to mathematics and, when not sentencing priests to be burnt at the stake, Fermat dedicated himself to his hobby. Fermat was a true amateur academic, a man whom E.T. Bell called the ‘Prince of Amateurs’. But so great were his talents that when Julian Coolidge wrote Mathematics of Great Amateurs, he excluded Fermat on the grounds that he was ‘so really great that he should count as a professional’.
At the start of the seventeenth century, mathematics was still recovering from the Dark Ages and was not a highly regarded subject. Similarly mathematicians were not treated with great respect and most of them had to fund their own studies. For example, Galileo was unable to study mathematics at the University of Pisa and was forced to seek private tuition. Indeed, the only institute in Europe to actively encourage mathematicians was Oxford University which had established the Savilian Chair of Geometry in 1619. It is true to say that most seventeenth-century mathematicians were amateurs, but Fermat was an extreme case. Living far from Paris he was isolated from the small community of mathematicians that did exist, which included such figures as Pascal, Gassendi, Roberval, Beaugrand and most notably Father Marin Mersenne.
Father Mersenne made only minor contributions to number theory and yet he played a role in seventeenth-century mathematics which was arguably more important than any of his more esteemed colleagues. After joining the order of Minims in 1611, Mersenne studied mathematics and then taught the subject to other monks and to nuns at the Minim convent at Nevers. Eight years later he moved to Paris to join the Minims de l’Annociade, close to the Place Royale, a natural gathering place for intellectuals. Inevitably Mersenne met the other mathematicians of Paris, but he was saddened by their reluctance to talk to him or to each other.
The secretive nature of the Parisian mathematicians was a tradition which had been passed down from the cossists of the sixteenth century. The cossists were experts in calculations of all kinds and were employed by merchants and businessmen to solve complex accounting problems. Their name derives from the Italian word cosa, meaning ‘thing’, because they used symbols to represent an unknown quantity, similar to the way mathematicians use x today. All professional problem-solvers of this era invented their own clever methods for performing calculations and would do their utmost to keep these methods secret in order to maintain their reputation as the only person capable of solving a particular problem. On one exceptional occasion Niccolò Tartaglia, who had found a method for quickly solving cubic equations, revealed his discovery to Girolamo Cardano and swore him to absolute secrecy. Ten years later Cardano broke his promise and published Tartaglia’s method in his Ars Magna, an act which Tartaglia would never forgive. He broke off all relations with Cardano and a bitter public dispute ensued, which only served to further encourage other mathematicians to guard their secrets. The secretive nature of mathematicians continued right up until the end of the nineteenth century, and as we shall see later there are even examples of secret geniuses working in the twentieth century.
When Father Mersenne arrived in Paris he was determined to fight against the ethos of secrecy and tried to encourage mathematicians to exchange their ideas and build upon each other’s work. The monk arranged regular meetings and his group later formed the core of the French Academy. When anyone refused to attend, Mersenne would pass on to the group whatever he could by revealing letters and papers – even if they had been sent to him in confidence. It was not ethical behaviour for a man of the cloth, but he justified it on the grounds that the exchange of information would benefit mathematics and mankind. These acts of indiscretion naturally caused bitter arguments between the well-meaning monk and the taciturn prima donnas, and eventually destroyed Mersenne’s relationship with Descartes which had lasted since the two men had studied together at the Jesuit College of La Flèche. Mersenne had revealed philosophical writings by Descartes which were liable to offend the Church, but to his credit he did defend Descartes against theological attacks, as in fact he had done earlier in the case of Galileo. In an era dominated by religion and magic Mersenne stood up for rational thought.
Mersenne travelled throughout France and further afield, spreading news of the latest discoveries. In his travels he would make a point of meeting up with Pierre de Fermat and, indeed, seems to have been Fermat’s only regular contact with other mathematicians. Mersenne’s influence on this Prince of Amateurs must have been second only to the Arithmetica, a mathematical treatise handed down from the ancient Greeks which was Fermat’s constant companion. Even when he was unable to travel Mersenne would maintain his relationship with Fermat and others by writing prolifically. After Mersenne’s death his room was found stacked with letters written by seventy-eight different correspondents.
Despite the encouragement of Father Mersenne, Fermat steadfastly refused to reveal his proofs. Publication and recognition meant nothing to him and he was satisfied with the simple pleasure of being able to create new theorems undisturbed. However, the shy and retiring genius did have a mischievous streak, which, when combined with his secrecy, meant that when he did sometimes communicate with other mathematicians it was only to tease them. He would write letters stating his most recent theorem without providing the accompanying proof. Then he would challenge his contemporaries to find the proof. The fact that he would never reveal his own proofs caused a great deal of frustration. Rene Descartes called Fermat a ‘braggart’ and the Englishman John Wallis referred to him as ‘That damned Frenchman’. Unfortunately for the English, Fermat took particular pleasure in toying with his cousins across the Channel.
As well as having the satisfaction of annoying his colleagues, Fermat’s habit of stating a problem but hiding its solution did have more practical motivations. First, it meant that he did not have to waste time fully fleshing out his methods; instead he could rapidly proceed to his next conquest. Furthermore, he did not have to suffer jealous nit-picking. Once published, proofs would be examined and argued over by everyone and anyone who knew anything about the subject. When Blaise Pascal pressed him to publish some of his work, the recluse replied: ‘Whatever of my work is judged worthy of publication, I do not want my name to appear there.’ Fermat was the secretive genius who sacrificed fame in order not to be distracted by petty questions from his critics.
This exchange of letters with Pascal, the only occasion when Fermat discussed ideas with anyone but Mersenne, concerned the creation of an entirely new branch of mathematics – probability theory. The mathematical hermit was introduced to the subject by Pascal, and so, despite his desire for isolation, he felt obliged to maintain a dialogue. Together Fermat and Pascal would discover the first proofs and cast-iron certainties in probability theory, a subject which is inherently uncertain. Pascal’s interest in the subject had been sparked by a professional Parisian gambler, Antoine Gombaud, the Chevalier de Méré, who had posed a problem which concerned a game of chance called points. The game involves winning points on the roll of a dice, and whichever player is the first to earn a certain number of points is the winner and takes the prize money.
Gombaud had been involved in a game of points with a fellow-gambler when they were forced to abandon the game half-way through, owing to a pressing engagement. The problem then arose as to what to do with the prize money. The simple solution would have been to have given all the money to the competitor with the most points, but Gombaud asked Pascal if there was a fairer way to divide the money. Pascal was asked to calculate the probability of each player winning had the game continued and assuming that both players would have had an equal chance of winning subsequent points. The prize money could then be split according to these calculated probabilities.
Prior to the seventeenth century the laws of probability were defined by the intuition and experience of gamblers, but Pascal entered into an exchange of letters with Fermat with the aim of discovering the mathematical rules which more accurately describe the laws of chance. Three centuries later Bertrand Russell would comment on this apparent oxymoron: ‘How dare we speak of the laws of chance? Is not chance the antithesis of all law?’
The Frenchmen analysed Gombaud’s question and soon realised that it was a relatively trivial problem which could be solved by rigorously defining all the potential outcomes of the game and assigning an individual probability to each one. Both Pascal and Fermat were capable of independently solving Gombaud’s problem, but their collaboration speeded up the discovery of a solution and led them to a deeper exploration of other more subtle and sophisticated questions related to probability.
Probability problems are sometimes controversial because the mathematical answer, the true answer, is often contrary to what intuition might suggest. This failure of intuition is perhaps surprising because ‘survival of the fittest’ ought to provide a strong evolutionary pressure in favour of a brain naturally capable of analysing questions of probability. You can imagine our ancestors stalking a young deer, and weighing up whether or not to attack. What is the risk that a stag is nearby ready to defend its offspring and injure its assailant? On the other hand what is the chance that a better opportunity for a meal might arise if this one is judged too risky? A talent for analysing probability should be part of our genetic makeup and yet often our intuition misleads us.
One of the most counterintuitive probability problems concerns the likelihood of sharing birthdays. Imagine a football pitch with 23 people on it, the players and the referee. What is the probability that any two of those 23 people share the same birthday? With 23 people and 365 birthdays to chose from, it would seem highly unlikely that anybody would share the same birthday. If asked to put a figure on it most people would guess a probability of perhaps 10% at most. In fact, the actual answer is just over 50% – that is to say, on the balance of probability, it is more likely than not that two people on the pitch will share the same birthday.
The reason for this high probability is that what matters more than the number of people is the number of ways people can be paired. When we look for a shared birthday, we need to look at pairs of people not individuals. Whereas there are only 23 people on the pitch, there are 253 pairs of people. For example, the first person can be paired with any of the other 22 people giving 22 pairings to start with. Then, the second person can be paired with any of the remaining 21 people (we have already counted the second person paired with the first person so the number of possible pairings is reduced by one), giving an additional 21 pairings. Then, the third person can be paired with any of the remaining 20 people, giving an additional 20 pairings, and so on until we reach a total of 253 pairs.
The fact that the probability of a shared birthday within a group of 23 people is more than 50% seems intuitively wrong, and yet it is mathematically undeniable. Strange probabilities such as this are exactly what bookmakers and gamblers rely on in order to exploit the unwary. The next time you are at a party with more than 23 people you might want to make a wager that two people in the room will share a birthday. Please note that with a group of 23 people the probability is only slightly more than 50%, but the probability rapidly rises as the group increases in size. Hence, with a party of 30 people it is certainly worth betting that two of them will share the same birthday.
Fermat and Pascal founded the essential rules which govern all games of chance and which can be used by gamblers to define perfect playing and betting strategies. Furthermore, these laws of probability have found applications in a whole series of situations, ranging from speculating on the stock market to estimating the probability of a nuclear accident. Pascal was even convinced that he could use his theories to justify a belief in God. He stated that ‘the excitement that a gambler feels when making a bet is equal to the amount he might win multiplied by the probability of winning it’. He then argued that the possible prize of eternal happiness has an infinite value and that the probability of entering heaven by leading a virtuous life, no matter how small, is certainly finite. Therefore, according to Pascal’s definition, religion was a game of infinite excitement and one worth playing, because multiplying an infinite prize by a finite probability results in infinity.
As well as sharing the parentage of probability theory, Fermat was deeply involved in the founding of another area of mathematics, calculus. Calculus is the ability to calculate the rate of change, known as the derivative, of one quantity with respect to another. For example, the rate of change of distance with respect to time is better known simply as velocity. For mathematicians the quantities tend to be abstract and intangible but the consequences of Fermat’s work were to revolutionise science. Fermat’s mathematics enabled scientists to better understand the concept of velocity and its relation to other fundamental quantities such as acceleration – the rate of change of velocity with respect to time.
Economics is a subject heavily influenced by calculus. Inflation is the rate of change of price, known as the derivative of price, and furthermore economists are often interested in the rate of change of inflation, known as the second derivative of price. These terms are frequently used by politicians and the mathematician Hugo Rossi once observed the following: ‘In the fall of 1972 President Nixon announced that the rate of increase of inflation was decreasing. This was the first time a sitting president used a third derivative to advance his case for re-election.’
For centuries Isaac Newton was thought to have discovered calculus independently and without any knowledge of Fermat’s work, but in 1934 Louis Trenchard Moore discovered a note which set the record straight and gave Fermat the credit he deserves. Newton wrote that he developed his calculus based on ‘Monsieur Fermat’s method of drawing tangents’. Ever since the seventeenth century calculus has been used to describe Newton’s law of gravity and his laws of mechanics, which depend on distance, velocity and acceleration.
The discovery of calculus and probability theory would have been more than enough to earn Fermat a place in the mathematicians’ hall of fame, but his greatest achievement was in yet another branch of mathematics. While calculus has since been used to send rockets to the moon, and while probability theory has been used for risk assessment by insurance companies, Fermat’s greatest love was for a subject which is largely useless – the theory of numbers. Fermat was driven by an obsession to understand the properties of and the relationships between numbers. This is the purest and most ancient form of mathematics and Fermat was building on a body of knowledge that had been handed down to him from Pythagoras.
After Pythagoras’ death the concept of mathematical proof rapidly spread across the civilised world, and two centuries after his School was burnt to the ground the hub of mathematical study had moved from Croton to the city of Alexandria. In 332 BC, having conquered Greece, Asia Minor and Egypt, Alexander the Great decided that he would build a capital city that would be the most magnificent in the world. Alexandria was indeed a spectacular metropolis but not immediately a centre of learning. It was only when Alexander died and his half-brother Ptolemy I ascended the throne of Egypt that Alexandria became home to the world’s first-ever university. Mathematicians and other intellectuals flocked to Ptolemy’s city of culture, and although they were certainly drawn by the reputation of the university, the main attraction was the Alexandrian Library.
The Library was the idea of Demetrius Phalaerus, an unpopular orator who had been forced to flee Athens, and who eventually found sanctuary in Alexandria. He persuaded Ptolemy to gather together all the great books, assuring him that the great minds would follow. Once the tomes of Egypt and Greece had been installed, agents scoured Europe and Asia Minor in search of further volumes of knowledge. Even tourists to Alexandria could not escape the voracious appetite of the Library. Upon entering the city, their books were confiscated and taken to the scribes. The books were copied so that while the original was donated to the Library, a duplicate could graciously be given to the original owner. This meticulous replication service for ancient travellers gives today’s historians some hope that a copy of a great lost text will one day turn up in an attic somewhere in the world. In 1906 J.L. Heiberg discovered in Constantinople just such a manuscript, The Method, which contained some of Archimedes’ original writings.
Ptolemy’s dream of building a treasure house of knowledge lived on after his death, and by the time a few more Ptolemys had ascended the throne the Library contained over 600,000 books. Mathematicians could learn everything in the known world by studying at Alexandria, and there to teach them were the most famous academics. The first head of the mathematics department was none other than Euclid.
Euclid was born in about 330 BC. Like Pythagoras, Euclid believed in the search for mathematical truth for its own sake and did not look for applications in his work. One story tells of a student who questioned him about the use of the mathematics he was learning. Upon completing the lesson, Euclid turned to his slave and said, ‘Give the boy a penny since he desires to profit from all that he learns.’ The student was then expelled.
Euclid devoted much of his life to writing the Elements, the most successful textbook in history. Until this century it was also the second best-selling book in the world after the Bible. The Elements consists of thirteen books, some of which are devoted to Euclid’s own work, and the remainder being a compilation of all the mathematical knowledge of the age, including two volumes devoted entirely to the works of the Pythagorean Brotherhood. In the centuries since Pythagoras, mathematicians had invented a variety of logical techniques which could be applied in different circumstances, and Euclid skilfully employed them all in the Elements. In particular Euclid exploited a logical weapon known as reductio ad absurdum, or proof by contradiction. The approach revolves around the perverse idea of trying to prove that a theorem is true by first assuming that the theorem is false. The mathematician then explores the logical consequences of the theorem being false. At some point along the chain of logic there is a contradiction (e.g. 2 + 2 = 5). Mathematics abhors a contradiction and therefore the original theorem cannot be false, i.e. it must be true.
The English mathematician G.H. Hardy encapsulated the spirit of proof by contradiction in his book A Mathematician’s Apology: ‘Reductio ad absurdum, which Euclid loved so much, is one of a mathematician’s finest weapons. It is a far finer gambit than any chess play: a chess player may offer the sacrifice of a pawn or even a piece, but a mathematician offers the game.’
One of Euclid’s most famous proofs by contradiction established the existence of so-called irrational numbers. It is suspected that irrational numbers were originally discovered by the Pythagorean Brotherhood centuries earlier, but the concept was so abhorrent to Pythagoras that he denied their existence.
When Pythagoras claimed that the universe is governed by numbers he meant whole numbers and ratios of whole numbers (fractions) together known as rational numbers. An irrational number is a number that is neither a whole number nor a fraction, and this is what made it so horrific to Pythagoras. In fact, irrational numbers are so strange that they cannot be written down as decimals, even recurring decimals. A recurring decimal such as 0.111111 … is in fact a fairly straightforward number, and is equivalent to the fraction 1⁄9. The fact that the ‘1’ repeats itself forever means that the decimal has a very simple and regular pattern. This regularity, despite the fact that it continues to infinity, means that the decimal can be rewritten as a fraction. However, if you attempt to express an irrational number as a decimal you end up with a number which continues forever with no regular or consistent pattern.
The concept of an irrational number was a tremendous breakthrough. Mathematicians were looking beyond the whole numbers and fractions around them, and discovering, or perhaps inventing, new ones. The nineteenth-century mathematician Leopold Kronecker said, ‘God made the integers; all the rest is the work of man.’
The most famous irrational number is π. In schools it is sometimes approximated by 31⁄7 or 3.14; however, the true value of π is nearer 3.14159265358979323846, but even this is only an approximation. In fact, π can never be written down exactly because the decimal places go on forever without any pattern. A beautiful feature of this random pattern is that it can be computed using an equation which is supremely regular:
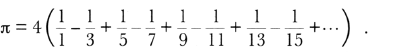
By calculating the first few terms, you can obtain a very rough value for π, but by calculating more and more terms an increasingly accurate value is achieved. Although knowing π to 39 decimal places is sufficient to calculate the circumference of the universe accurate to the radius of a hydrogen atom, this has not prevented computer scientists from calculating π to as many decimal places as possible. The current record is held by Yasumasa Kanada of the University of Tokyo who calculated π to six billion decimal places in 1996. Recently rumours have suggested that the Russian Chudnovsky brothers in New York have calculated π to eight billion decimal places and that they are aiming to reach a trillion decimal places. However, even if Kanada or the Chudnovsky brothers carried on calculating until their computers sapped all the energy in the universe, they would still not have found the exact value of π. It is easy to appreciate why Pythagoras conspired to hide the existence of these mathematical beasts.
The value of π to over 1500 decimal places

When Euclid dared to confront the issue of irrationality in the tenth volume of the Elements the goal was to prove that there could be a number which could never be written as a fraction. Instead of trying to prove that π is irrational, he examined the square root of two, √2 – the number which when multiplied by itself is equal to two. In order to prove that √2 could not be written as a fraction Euclid used reductio ad absurdum and began by assuming that it could be written as a fraction. He then demonstrated that this hypothetical fraction could be simplified. Simplification of a fraction means, for example, that the fraction 8⁄12 can be simplified to 4⁄6 by dividing top and bottom by 2. In turn 4⁄6 can be simplified to 2⁄3, which cannot be simplified any further and therefore the fraction is then said to be in its simplest form. However, Euclid showed that his hypothetical fraction, which was supposed to represent √2, could be simplified not just once, but over and over again an infinite number of times without ever reducing to its simplest form. This is absurd because all fractions must eventually have a simplest form, and therefore the hypothetical fraction cannot exist. Therefore √2 cannot be written as a fraction and is irrational. An outline of Euclid’s proof is given in Appendix 2.
By using proof by contradiction Euclid was able to prove the existence of irrational numbers. For the first time numbers had taken on a new and more abstract quality. Until this point in history all numbers could be expressed as whole numbers or fractions, but Euclid’s irrational numbers defied representation in the traditional manner. There is no other way to describe the number equal to the square root of two other than by expressing it as √2, because it cannot be written as a fraction and any attempt to write it as a decimal could only ever be an approximation, e.g. 1.414213562373 …
For Pythagoras, the beauty of mathematics was the idea that rational numbers (whole numbers and fractions) could explain all natural phenomena. This guiding philosophy blinded Pythagoras to the existence of irrational numbers and may even have led to the execution of one of his pupils. One story claims that a young student by the name of Hippasus was idly toying with the number √2, attempting to find the equivalent fraction. Eventually he came to realise that no such fraction existed, i.e. that √2 is an irrational number. Hippasus must have been overjoyed by his discovery, but his master was not. Pythagoras had defined the universe in terms of rational numbers, and the existence of irrational numbers brought his ideal into question. The consequence of Hippasus’ insight should have been a period of discussion and contemplation during which Pythagoras ought to have come to terms with this new source of numbers. However, Pythagoras was unwilling to accept that he was wrong, but at the same time he was unable to destroy Hippasus’ argument by the power of logic. To his eternal shame he sentenced Hippasus to death by drowning.
The father of logic and the mathematical method had resorted to force rather than admit he was wrong. Pythagoras’ denial of irrational numbers is his most disgraceful act and perhaps the greatest tragedy of Greek mathematics. It was only after his death that irrationals could be safely resurrected.
Although Euclid clearly had an interest in the theory of numbers, it was not his greatest contribution to mathematics. Euclid’s true passion was geometry, and of the thirteen volumes that make up the Elements, books I to VI concentrate on plane (two-dimensional) geometry and books XI to XIII deal with solid (three-dimensional) geometry. It is such a complete body of knowledge that the contents of the Elements would form the geometry syllabus in schools and universities for the next two thousand years.
The mathematician who compiled the equivalent text for number theory was Diophantus of Alexandria, the last champion of the Greek mathematical tradition. Although Diophantus’ achievements in number theory are well documented in his books, virtually nothing else is known about this formidable mathematician. His place of birth is unknown and his arrival in Alexandria could have been any time within a five-century window. In his writings Diophantus quotes Hypsicles and therefore he must have lived after 150 BC; on the other hand his own work is quoted by Theon of Alexandria and therefore he must have lived before AD 364. A date around AD 250 is generally accepted as being a sensible estimate. Appropriately for a problem-solver, the one detail of Diophantus’ life that has survived is in the form of a riddle said to have been carved on his tomb:
God granted him to be a boy for the sixth part of his life, and adding a twelfth part to this, He clothed his cheeks with down; He lit him the light of wedlock after a seventh part, and five years after his marriage He granted him a son. Alas! late-born wretched child; after attaining the measure of half his father’s full life, chill Fate took him. After consoling his grief by this science of numbers for four years he ended his life.
The challenge is to calculate Diophantus’ life span. The answer can be found in Appendix 3.
This riddle is an example of the sort of problem that Diophantus relished. His speciality was to tackle questions which required whole number solutions, and today such questions are referred to as Diophantine problems. He spent his career in Alexandria collecting well-understood problems and inventing new ones, and then compiled them all into a major treatise entitled Arithmetica. Of the thirteen books which made up the Arithmetica, only six would survive the turmoils of the Dark Ages and go on to inspire the Renaissance mathematicians, including Pierre de Fermat. The remaining seven books would be lost during a series of tragic events which would send mathematics back to the age of the Babylonians.
During the centuries between Euclid and Diophantus, Alexandria remained the intellectual capital of the civilised world, but throughout this period the city was continually under threat from foreign armies. The first major attack occurred in 47 BC, when Julius Caesar attempted to overthrow Cleopatra by setting fire to the Alexandrian fleet. The Library, which was located near the harbour, also caught alight, and hundreds of thousands of books were destroyed. Fortunately for mathematics Cleopatra appreciated the importance of knowledge and was determined to restore the Library to its former glory. Mark Antony realised that the way to an intellectual’s heart is via her library, and so marched to the city of Pergamum. This city had already initiated a library which it hoped would provide it with the best collection in the world, but instead Mark Antony transplanted the entire stock to Egypt, restoring the supremacy of Alexandria.
For the next four centuries the Library continued to accumulate books until in AD 389 it received the first of two fatal blows, both the result of religious bigotry. The Christian Emperor Theodosius ordered Theophilus, Bishop of Alexandria, to destroy all pagan monuments. Unfortunately when Cleopatra rebuilt and restocked the Library, she decided to house it in the Temple of Serapis, and so the Library became caught up in the destruction of icons and altars. The ‘pagan’ scholars attempted to save six centuries-worth of knowledge, but before they could do anything they were butchered by the Christian mob. The descent into the Dark Ages had begun.
A few precious copies of the most vital books survived the Christian onslaught and scholars continued to visit Alexandria in search of knowledge. Then in 642 a Moslem attack succeeded where the Christians had failed. When asked what should be done with the Library, the victorious Caliph Omar commanded that those books that were contrary to the Koran should be destroyed, and furthermore those books that conformed to the Koran were superfluous and they too must be destroyed. The manuscripts were used to stoke the furnaces which heated the public baths and Greek mathematics went up in smoke. It is not surprising that most of Diophantus’ work was destroyed; in fact it is a miracle that six volumes of the Arithmetica managed to survive the tragedy of Alexandria.
For the next thousand years mathematics in the West was in the doldrums, and only a handful of luminaries in India and Arabia kept the subject alive. They copied the formulae described in the surviving manuscripts of Greece and then began to reinvent for themselves many of the theorems that had been lost. They also added new elements to mathematics, including the number zero.
In modern mathematics zero performs two functions. First, it allows us to distinguish between numbers like 52 and 502. In a system where the position of a number denotes its value, a symbol is needed to confirm an empty position. For instance, 52 represents 5 times ten plus 2 times one, whereas 502 represents 5 times a hundred plus 0 times ten plus 2 times one, and the zero is crucial for removing any ambiguity. Even the Babylonians in the third millennium BC appreciated the use of zero to avoid confusion, and the Greeks adopted their idea, using a circular symbol similar to the one we use today. However, zero has a more subtle and deeper significance which was only fully appreciated several centuries later by the mathematicians of India. The Hindus recognised that zero had an independent existence beyond the mere spacing role among the other numbers – zero was a number in its own right. It represented a quantity of nothing. For the first time the abstract concept of nothingness had been given a tangible symbolic representation.
This may seem a trivial step forward to the modern reader, but the deeper meaning of the zero symbol had been ignored by all the ancient Greek philosophers, including Aristotle. He had argued that the number zero should be outlawed because it disrupted the consistency of the other numbers – dividing any ordinary number by zero led to an incomprehensible result. By the sixth century the Indian mathematicians no longer brushed this problem under the rug, and the seventh-century scholar Brahmagupta was sophisticated enough to use division by zero as a definition for infinity.
While Europe had abandoned the noble search for truth, India and Arabia were consolidating the knowledge which had been smuggled out of the embers of Alexandria and were reinterpreting it in a new and more eloquent language. As well as adding zero to the mathematical vocabulary, they replaced the primitive Greek symbols and cumbersome Roman numerals with the counting system which has now been universally adopted. Once again, this might seem like an absurdly humble step forward, but try multiplying CLV by DCI and you will appreciate the significance of the breakthrough. The equivalent task of multiplying 155 by 601 is a good deal simpler. The growth of any discipline depends on the ability to communicate and develop ideas, and this in turn relies on a language which is sufficiently detailed and flexible. The ideas of Pythagoras and Euclid were no less elegant for their awkward expression, but translated into the symbols of Arabia they would blossom and give fruit to newer and richer concepts.
In the tenth century the French scholar Gerbert of Aurillac learnt the new counting system from the Moors of Spain and through his teaching positions at churches and schools throughout Europe he was able to introduce the new system to the West. In 999 he was elected Pope Sylvester II, an appointment which allowed him to further encourage the use of Indo-Arabic numerals. Although the efficiency of the system revolutionised accounting and was rapidly adopted by merchants, it did little to inspire a revival in European mathematics.
The vital turning point for Western mathematics occurred in 1453 when the Turks ransacked Constantinople. During the intervening years the manuscripts which had survived the desecration of Alexandria had congregated in Constantinople, but once again they were threatened with destruction. Byzantine scholars fled westward with whatever texts they could preserve. Having survived the onslaught of Caesar, Bishop Theophilus, Caliph Omar and now the Turks, a few precious volumes of the Arithmetica made their way back to Europe. Diophantus was destined for the desk of Pierre de Fermat.
Fermat’s judicial responsibilities occupied a great deal of his time, but what little leisure he had was devoted entirely to mathematics. This was partly because judges in seventeenth-century France were discouraged from socialising on the grounds that friends and acquaintances might one day be called before the court. Fraternising with the locals would only lead to favouritism. Isolated from the rest of Toulouse’s high society, Fermat could concentrate on his hobby.
There is no record of Fermat ever being inspired by a mathematical tutor; instead it was a copy of the Arithmetica which became his mentor. The Arithmetica sought to describe the theory of numbers, as it was in Diophantus’ time, via a series of problems and solutions. In effect Diophantus was presenting Fermat with one thousand years worth of mathematical understanding. In one book Fermat could find the entire knowledge of numbers as constructed by the likes of Pythagoras and Euclid. The theory of numbers had stood still ever since the barbaric burning of Alexandria, but now Fermat was ready to resume study of the most fundamental of mathematical disciplines.
The Arithmetica which inspired Fermat was a Latin translation made by Claude Gaspar Bachet de Méziriac, reputedly the most learned man in all of France. As well as being a brilliant linguist, poet and classics scholar, Bachet had a passion for mathematical puzzles. His first publication was a compilation of puzzles entitled Problemes plaisans et délectables qui se font par les nombres, which included river-crossing problems, a liquid-pouring problem and several think-of-a-number tricks. One of the questions posed was a problem about weights:
What is the least number of weights that can be used on a set of scales to weigh any whole number of kilograms from 1 to 40?
Bachet had a cunning solution which shows that it is possible to achieve this task with only four weights. His solution is given in Appendix 4.
Although he was merely a mathematical dilettante, Bachet’s interest in puzzles was enough for him to realise that Diophantus’ list of problems were on a higher plane and worthy of deeper study. He set himself the task of translating Diophantus’ opus and publishing it so that the techniques of the Greeks could be rekindled. It is important to realise that vast quantities of ancient mathematical knowledge had been completely forgotten. Higher mathematics was not taught in even the greatest European universities and it is only thanks to the efforts of scholars such as Bachet that so much was revived so rapidly. In 1621 when Bachet published the Latin version of the Arithmetica, he was contributing to the second golden age of mathematics.
The Arithmetica contains over one hundred problems and for each one Diophantus gives a detailed solution. This level of conscientiousness was not a habit which Fermat ever picked up. Fermat was not interested in writing a textbook for future generations: he merely wanted to satisfy himself that he had solved a problem. While studying Diophantus’ problems and solutions, he would be inspired to think of and tackle other related and more subtle questions. Fermat would scribble down whatever was necessary to convince himself that he could see the solution and then he would not bother to write down the remainder of the proof. More often than not he would consign his inspirational jottings to the bin, and then move on to the next problem. Fortunately for us, Bachet’s publication of the Arithmetica contained generous margins on every page, and sometimes Fermat would hastily write logic and comments in these columns. These marginal notes would become an invaluable, if somewhat scanty, record of Fermat’s most brilliant calculations.
One of Fermat’s discoveries concerned the so-called friendly numbers, or amicable numbers, closely related to the perfect numbers which had fascinated Pythagoras two thousand years earlier. Friendly numbers are pairs of numbers such that each number is the sum of the divisors of the other number. The Pythagoreans made the extraordinary discovery that 220 and 284 are friendly numbers. The divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, and the sum of all these is 284. On the other hand the divisors of 284 are 1, 2, 4, 71, 142, and the sum of all these is 220.
The pair 220 and 284 was said to be symbolic of friendship. Martin Gardner’s book Mathematical Magic Show tells of talismans sold in the Middle Ages which were inscribed with these numbers on the grounds that wearing the charms would promote love. An Arab numerologist documents the practice of carving 220 on one fruit and 284 on another, and then eating the first one and offering the second one to a lover as a form of mathematical aphrodisiac. Early theologians noted that in Genesis Jacob gave 220 goats to Esau. They believed that the number of goats, one half of a friendly pair, was an expression of Jacob’s love for Esau.
No other friendly numbers were identified until 1636 when Fermat discovered the pair 17,296 and 18,416. Although not a profound discovery, it demonstrates Fermat’s familiarity with numbers and his love of playing with them. Fermat started a fad for finding friendly numbers; Descartes discovered a third pair (9,363,584 and 9,437,056) and Leonhard Euler went on to list sixty-two amicable pairs. Curiously they had all overlooked a much smaller pair of friendly numbers. In 1866 a sixteen-year-old Italian, Nicolò Paganini, discovered the pair 1,184 and 1,210.
During the twentieth century mathematicians have extended the idea further and have searched for so-called ‘sociable’ numbers, three or more numbers which form a closed loop. For example, in the loop of 5 numbers (12,496; 14,288; 15,472; 14,536; 14,264) the divisors of the first number add up to the second, the divisors of the second add to the third, the divisors of the third add up to the fourth, the divisors of the fourth add up to the fifth, and the divisors of the fifth add up to the first.
Although discovering a new pair of friendly numbers made Fermat something of a celebrity, his reputation was truly confirmed thanks to a series of mathematical challenges. For example, Fermat noticed that 26 is sandwiched between 25 and 27, one of which is a square number (25 = 52 = 5 × 5) and the other is a cube number (27 = 33 = 3 × 3 × 3). He searched for other numbers sandwiched between a square and a cube but failed to find any, and suspected that 26 might be unique. After days of strenuous effort he managed to construct an elaborate argument which proved without any doubt that 26 is indeed the only number between a square and a cube. His step-by-step logical proof established that no other numbers could fulfil this criterion.
Fermat announced this unique property of 26 to the mathematical community, and then challenged them to prove that this was the case. He openly admitted that he himself had a proof; the question was, however, did others have the ingenuity to match it? Despite the simplicity of the claim the proof is fiendishly complicated, and Fermat took particular delight in taunting the English mathematicians Wallis and Digby, who eventually had to admit defeat. Ultimately Fermat’s greatest claim to fame would turn out to be another challenge to the rest of the world. However, it would be an accidental riddle which was never intended for public discussion.
While studying Book II of the Arithmetica Fermat came upon a whole series of observations, problems and solutions which concerned Pythagoras’ theorem and Pythagorean triples. For instance, Diophantus discussed the existence of particular triples which formed so-called ‘limping triangles’, ones in which the two shorter legs x and y differ only by one (e.g. x = 20, y = 21, z = 29 and 202 + 212 = 292).
Fermat was struck by the variety and sheer quantity of Pythagorean triples. He was aware that centuries earlier Euclid had stated a proof, outlined in Appendix 5, which demonstrated that, in fact, there are an infinite number of Pythagorean triples. Fermat must have gazed at Diophantus’ detailed exposition of Pythagorean triples and wondered what there was to add to the subject. As he stared at the page he began to play with Pythagoras’ equation, trying to discover something which had evaded the Greeks. Suddenly, in a moment of genius which would immortalise the Prince of Amateurs, he created an equation which, though very similar to Pythagoras’ equation, had no solutions at all. This was the equation which the ten-year-old Andrew Wiles read about in the Milton Road Library.
Instead of considering the equation
![]()
Fermat was contemplating a variant of Pythagoras’ creation:
![]()
As mentioned in the last chapter, Fermat had merely changed the power from 2 to 3, the square to a cube, but his new equation apparently had no whole number solutions whatsoever. Trial and error soon shows the difficulty of finding two cubed numbers which add together to make another cubed number. Could it really be the case that this minor modification turns Pythagoras’ equation, one with an infinite number of solutions, into an equation with no solutions?
He altered the equation further by changing the power to numbers bigger than 3, and discovered that finding a solution to each of these equations was equally difficult. According to Fermat there appeared to be no three numbers which would perfectly fit the equation
![]()
In the margin of his Arithmetica, next to Problem 8, he made a note of his observation:
Cubem autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere.
It is impossible for a cube to be written as a sum of two cubes or a fourth power to be written as the sum of two fourth powers or, in general, for any number which is a power greater than the second to be written as a sum of two like powers.
Among all the possible numbers there seemed to be no reason why at least one set of solutions could not be found, yet Fermat stated that nowhere in the infinite universe of numbers was there a ‘Fermatean triple’. It was an extraordinary claim, but one which Fermat believed he could prove. After the first marginal note outlining the theory, the mischievous genius jotted down an additional comment which would haunt generations of mathematicians:
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caperet.
I have a truly marvellous demonstration of this proposition which this margin is too narrow to contain.
This was Fermat at his most infuriating. His own words suggest that he was particularly pleased with this ‘truly marvellous’ proof, but he had no intention of bothering to write out the detail of the argument, never mind publishing it. He never told anyone about his proof, and yet despite his combination of indolence and modesty Fermat’s Last Theorem, as it would later be called, would become famous around the world for centuries to come.
Fermat’s notorious discovery happened early in his mathematical career, in around 1637. Some thirty years later, while carrying out his judicial duties in the town of Castres, Fermat was taken seriously ill. On 9 January 1665, he signed his last arrêt, and three days later he died. Still isolated from the Parisian school of mathematics and not necessarily fondly remembered by his frustrated correspondents, Fermat’s discoveries were at risk of being lost forever. Fortunately Fermat’s eldest son, Clément-Samuel, who appreciated the significance of his father’s hobby, was determined that his discoveries should not be lost to the world. It is thanks to his efforts that we know anything at all about Fermat’s remarkable breakthroughs in number theory and, in particular, if it were not for Clément-Samuel, the enigma known as Fermat’s Last Theorem would have died with its creator.
Clément-Samuel spent five years collecting his father’s notes and letters, and examining the jottings in the margins of his copy of the Arithmetica. The marginal note referring to Fermat’s Last Theorem was just one of many inspirational thoughts scribbled in the book, and Clément-Samuel undertook to publish these annotations in a special edition of the Arithmetica. In 1670 at Toulouse he brought out Diophantus’ Arithmetica Containing Observations by P. de Fermat. Alongside Bachet’s original Greek and Latin translations were forty-eight observations made by Fermat, one of which was to become known as Fermat’s Last Theorem.
Once Fermat’s Observations reached the wider community, it was clear that the letters he had sent to colleagues represented mere morsels from a treasure trove of discovery. His personal notes contained a whole series of theorems. Unfortunately these were accompanied either with no explanation at all or with only a slight hint of the underlying proof. There were just enough tantalising glimpses of logic to leave mathematicians in no doubt that Fermat had proofs, but filling in the details was left as a challenge for them to take up.
Leonhard Euler, one of the greatest mathematicians of the eighteenth century, attempted to prove one of Fermat’s most elegant observations, a theorem concerning prime numbers. A prime number is one which has no divisors – no number will divide into it without a remainder, except for 1 and the number itself. For instance, 13 is a prime number, but 14 is not. Nothing will divide into 13, but 2 and 7 will divide into 14. All prime numbers (except 2) can be put into two categories; those which equal 4n + 1 and those which equal 4n – 1, where n equals some number. So 13 is in the former group (4 × 3 + 1), whereas 19 is in the latter group (4 × 5 – 1). Fermat’s prime theorem claimed that the first type of primes were always the sum of two squares (13 = 22 + 32), whereas the second type could never be written in this way (19 = ?2 + ?2). This property of primes is beautifully simple, but trying to prove that it is true for every single prime number turns out to be remarkably difficult. For Fermat it was just one of many private proofs. The challenge for Euler was to rediscover Fermat’s proof. Eventually in 1749, after seven years work and almost a century after Fermat’s death, Euler succeeded in proving this prime number theorem.
Fermat’s panoply of theorems ranged from the fundamental to the simply amusing. Mathematicians rank the importance of theorems according to their impact on the rest of mathematics. First, a theorem is considered important if it has a universal truth, that is to say, if it applies to an entire group of numbers. In the case of the prime number theorem, it is true not for just some prime numbers, but for all prime numbers. Second, theorems should reveal some deeper underlying truth about the relationship between numbers. A theorem can be the springboard for generating a whole host of other theorems, even inspiring the development of whole new branches of mathematics. Finally, a theorem is important if entire areas of research can be hindered for the lack of one logical link. Many mathematicians have cried themselves to sleep knowing that they could achieve a major result if only they could establish one missing link in their chain of logic.
Because mathematicians employ theorems as stepping stones to other results, it was essential that every single one of Fermat’s theorems be proved. Just because Fermat said he had a proof of a theorem it could not be accepted at face value. Before it could be used, each theorem had to be proved with ruthless rigour, otherwise the consequences could have been disastrous. For example, imagine that mathematicians had accepted one of Fermat’s theorems. It would then be incorporated as a single element in a whole series of other larger proofs. In due course these larger proofs would be incorporated into even larger proofs, and so on. Ultimately hundreds of theorems could come to rely on the truth of the original unchecked theorem. However, what if Fermat had made a mistake and the unchecked theorem was in fact flawed? All these other theorems which incorporated it would also be flawed, and vast areas of mathematics would collapse. Theorems are the foundations of mathematics, because once their truth has been established other theorems can safely be built on top of them. Unsubstantiated ideas are infinitely less valuable and are referred to as conjectures. Any logic which relies on a conjecture is itself a conjecture.
Fermat said he had a proof for every one of his observations, so for him they were theorems. However, until the community at large could rediscover the individual proofs each one could only be considered a conjecture. In fact for the last 350 years Fermat’s Last Theorem should more accurately have been referred to as Fermat’s Last Conjecture.
As the centuries passed, all his other observations were proved one by one, but Fermat’s Last Theorem stubbornly refused to give in so easily. In fact, it is called the ‘Last’ Theorem because it remains the last one of the observations to be proved. Three centuries of effort failed to find a proof, and this led to its notoriety as the most demanding riddle in mathematics. However, this acknowledged difficulty does not necessarily mean that Fermat’s Last Theorem is an important theorem in the ways described earlier. The Last Theorem, at least until very recently, seemed to fail to fulfil several criteria – it seemed that proving it would not lead to anything profound, it would not give any particularly deep insight about numbers, and it would not help prove any other conjectures.
The fame of Fermat’s Last Theorem comes solely from the sheer difficulty of proving it. An extra sparkle is added by the fact that the Prince of Amateurs said that he could prove this theorem which has since baffled generations of professional mathematicians. Fermat’s offhand comments in the margin of his copy of the Arithmetica were read as a challenge to the world. He had proved the Last Theorem: the question was, could any mathematician match his brilliance?
G.H. Hardy had a whimsical sense of humour and dreamt up what could have been an equally frustrating legacy. Hardy’s challenge was in the form of an insurance policy to help him cope with his fear of travelling on ships. If he ever had to journey across the sea he would first send a telegram to a colleague saying:
HAVE SOLVED RIEMANN HYPOTHESIS STOP
WILL GIVE DETAILS UPON RETURN STOP
The Riemann hypothesis is a problem which has plagued mathematicians since the nineteenth century. Hardy’s logic was that God would never allow him to drown because it would leave mathematicians haunted by a second terrible phantom.
Fermat’s Last Theorem is a problem of immense difficulty, and yet it can be stated in a form that a schoolchild can understand. There can be no problem in physics, chemistry or biology which can be so simply and unambiguously stated and which has remained unsolved for so long. In his book The Last Problem, E.T. Bell wrote that civilisation would probably come to an end before Fermat’s Last Theorem could be solved. Proving Fermat’s Last Theorem has become the most valuable prize in number theory, and not surprisingly it has led to some of the most exciting episodes in the history of mathematics. The search for a proof of Fermat’s Last Theorem has involved the greatest minds on the planet, huge rewards, suicidal despair and duelling at dawn.
The riddle’s status has gone beyond the closed world of mathematics. In 1958 it even made its way into a Faustian tale. An anthology entitled Deals with the Devil contains a short story written by Arthur Porges. In ‘The Devil and Simon Flagg’ the Devil asks Simon Flagg to set him a question. If the Devil succeeds in answering it within twenty-four hours then he takes Simon’s soul, but if he fails then he must give Simon $100,000. Simon poses the question: ‘Is Fermat’s Last Theorem correct?’ The Devil disappears and whizzes around the world to absorb every piece of mathematics that has ever been created. The following day he returns and admits defeat:
‘You win, Simon,’ he said, almost in a whisper, eyeing him with ungrudging respect. ‘Not even I can learn enough mathematics in such a short time for so difficult a problem. The more I got into it the worse it became. Non-unique factoring, ideals – Bah! Do you know,’ the Devil confided, ‘not even the best mathematicians on other planets – all far ahead of yours – have solved it? Why, there’s a chap on Saturn – he looks something like a mushroom on stilts – who solves partial differential equations mentally; and even he’s given up.’