I first saw David Bayer—or part of him, anyway—in a movie back in 2001. A lot of people saw him that year, although most of them, like me, didn’t know it at the time. That’s because they only got to see a small part of his anatomy: his hands. His body and his face and his voice—every other part of him—belonged to Russell Crowe. But the hands belonged to Bayer.
Bayer was Russell Crowe’s hand double in A Beautiful Mind, the film about mathematician John Nash. It was Bayer’s beautiful hands that scribbled enigmatic formulas on the chalkboards and windowpanes of an imaginary 1940s Princeton. The film’s producers wanted a movie with real math in it, unlike the fairy-tale Good Will Hunting. (Remember the problem on the chalkboard in the MIT hallway that supposedly took the faculty two years to solve? Turns out it was an elementary exercise in graph theory that moviegoing mathletes cracked during the few seconds it was on-screen.) So the producers of A Beautiful Mind brought Bayer on as a consultant and later as an actor, and to this day he still gets residuals for his handiwork. Come to think of it, I’d met (and shaken) a lot of famous hands in my time: Simon Lovell, who did Ed Norton’s base deals in Rounders; Xtreme Card Manipulator Dave Buck, whose talented fingers flourished for Jeremy Piven in Smokin’ Aces; magician and actor Christopher Hart, whose right hand played Thing in the Addams Family movies. And now Bayer.
His class met just after six o’clock on a crisp October evening in a small seminar room on the second floor of Milbank Hall, the oldest building on Barnard’s campus, across the street from Columbia. Bayer walked into the seminar room sporting jeans and a T-shirt. After a brief introduction, he removed a deck of cards from his leather bag. He handed them out for inspection and asked us to shuffle three times. Being the resident card expert, I did the shuffling. Bayer then asked me to pick a card at random and bury it in the middle of the pack, after which he took the deck and scanned through the faces of the cards. Moments later, he removed a lone card and held it up for all to see. “Was this it?” he asked, smiling. “The ace of hearts?” Of course it was.
It may not have been as dramatic as a levitation, but this to me was an astonishing trick. It was the shuffling that made no sense. How could he have let me shuffle, not once but three times? Wouldn’t all that shuffling lose the card forever? He couldn’t have used a key card or a crimp or daub or a marked deck. And clearly he wasn’t employing sophisticated gambling techniques à la Richard Turner. He was a math professor, not a magician. There was no gimmickry or sleight of hand involved. Even if he’d known the order of the cards beforehand, shuffling would have ruined it. There had to be a catch—and the catch, Bayer explained, had to do with the peculiar mathematical properties of shuffling.
The trick we’d just witnessed was a modified version of an effect originally conceived by an American magician and chicken farmer named Charles Jordan, who lived in rural California during the early twentieth century. Jordan never performed publicly—instead choosing to earn his keep by selling tricks, raising chickens, and winning mail-in puzzle contests—but he did invent a number of groundbreaking card sleights, including two false counts still widely in use.
His most enduring legacy, however, was something called Long-Distance Mind Reading, a magic trick performed by mail. In Jordan’s original version, the magician mails a deck of cards to the “spectator,” who cuts the cards in half and shuffles the two halves together. The deck is cut once more, and a lone card is removed from one of the two piles. After noting its identity, the spectator places the card in the middle of the other half and sends it back to the magician, who identifies the selection a few days later by return post.
Jordan published a small ad for the trick in the back of the Sphinx, the premier magic magazine of his day, in the spring of 1916. At the time, it went unnoticed, perhaps because the mail was so slow. For almost a century it was all but forgotten, lost in the mire of history, like a buried treasure waiting to be unearthed.
Until Persi Diaconis came along.
The Jordan trick caught his eye because it suggested something counterintuitive about shuffling, namely that shuffling doesn’t work as well as most people think it does. Being a magician and a gambling expert at heart—his second deals, I’ve heard, are second to none—Diaconis wanted to understand shuffling from a mathematical point of view. If shuffling truly randomizes the cards, he reasoned, then Jordan’s trick would be impossible, because there would be no systematic way of locating the selection once the cards had been mixed. The fact that it was possible meant that the conventional wisdom on shuffling had to be wrong.
While at Harvard, Diaconis teamed up with Bayer, who was a postdoc at the time, and together they set out to test this hypothesis. Their task was to determine how many shuffles it takes to adequately mix a deck of cards such that no trace of the original order remains. Only after solving this problem would they be able to decipher Jordan’s mind-reading mystery.
Their best lead was a technical memorandum written by a mathematician named Edgar Gilbert at Bell Labs, the research arm of AT&T, which had circulated in the fall of 1955. The memorandum sketched out the first useful mathematical model of card shuffling, one that laid the foundation for all subsequent work on the subject.
Why would the world’s largest phone company have been interested in card shuffling? It all came down to probability. The phone company uses complex probabilistic theories to model switchboard capacity. The phone network connects people all over the country, so it has to be extremely spread out, but it also must be capable of handling variations in call volume, otherwise a spike in the number of calls can overload the grid—much in the way that when Michael Jackson died the massive surge of Internet queries temporarily brought down Google News. “They want to model all these random processes, so they care about probability,” Bayer explained. “Card shuffling was very much in the spirit of what they were doing.”
The phone company was also interested in how information can be transmitted over staticky channels. In 1948, in a landmark paper, Bell Labs mathematician Claude Shannon founded the field of information theory, a branch of mathematics concerned with measuring and quantifying information. What began as a theoretical investigation into signal processing turned out to have profound consequences. Biologists now use information theory to study genetic codes. Physicists use it to understand the digestive system of black holes. To the extent that it laid out a formal set of rules for how data can be stored and transmitted, information theory—along with its offshoot, coding theory—provided the mathematical framework for the digital age.
Gilbert’s 1955 memo on shuffling analyzed the problem through the dual lenses of probability and information theory. A deck of cards can be viewed as containing a quantifiable amount of information. Think of each card as a number or a letter. Depending on how you arrange the deck, you can spell out different messages. Shuffling, meanwhile, erases the messages. It’s the static on the wire.
Roughly speaking, shuffling represents entropy—nature’s stubborn tendency toward disorder. Entropy is why you can turn an egg into an omelet but not an omelet into an egg. It’s why heat flows from hot objects to cold objects and not the other way around. It’s why ice melts. According to the second law of thermodynamics—which really isn’t a law so much as a statistical imperative—the entropy of the universe is always increasing, and this is ultimately why shuffling tends to mix up a deck of cards.
There are many ways to shuffle, of course, but the most common method—the one typically used in casinos—is the riffle shuffle. To do a riffle shuffle, you begin by splitting the deck into two roughly equal stacks. You then flick the cards with your thumbs off the bottoms of the piles in an alternating fashion, interlacing the two stacks. In theory, there are about as many combinations of fifty-two cards as there are particles in the Milky Way, but in practice, not all these combinations are likely, or even possible, after a few riffle shuffles.
For simplicity’s sake, let’s say we have just eight cards, the ace through eight of spades. We cut the deck into two equal piles—A 2
2 3
3 4
4 and 5
and 5 6
6 7
7 8
8 —and riffle them together. After the shuffle, the deck might look something like this: 5
—and riffle them together. After the shuffle, the deck might look something like this: 5 A
A 6
6 7
7 2
2 3
3 8
8 4
4 . The numbers are no longer in order, but you can still pick out the two original sequences. The riffle shuffle weaves the two sequences together, but it doesn’t jumble up the cards within each sequence. The ace always precedes the two, the two always precedes the three, the three always precedes the four, and so on. A single riffle shuffle might produce the string 5
. The numbers are no longer in order, but you can still pick out the two original sequences. The riffle shuffle weaves the two sequences together, but it doesn’t jumble up the cards within each sequence. The ace always precedes the two, the two always precedes the three, the three always precedes the four, and so on. A single riffle shuffle might produce the string 5 , 6
, 6 A
A 7
7 2
2 3
3 8
8 4
4 but never 3
but never 3 7
7 8
8 4
4 A
A 5
5 2
2 6
6 .
.
A single shuffle doubles the number of so-called rising sequences. A rising sequence is a sequence that’s always increasing, such as 5 , 6
, 6 , 7
, 7 , 8
, 8 . Shuffling once produces a combination with at most two rising sequences, and each additional shuffle no more than doubles that number. If you shuffle twice, for instance, the resulting combination contains at most four rising sequences. After three shuffles you get a maximum of eight, and so forth. It doesn’t always double every time, because you randomly lose some along the way, but you never wind up with more than twice as many rising sequences as in the preceding shuffle, and this is true no matter how many cards you use, be it eight or eight million. As a result, the number of rising sequences is like a barometer that tells you how thoroughly a deck has been mixed.
. Shuffling once produces a combination with at most two rising sequences, and each additional shuffle no more than doubles that number. If you shuffle twice, for instance, the resulting combination contains at most four rising sequences. After three shuffles you get a maximum of eight, and so forth. It doesn’t always double every time, because you randomly lose some along the way, but you never wind up with more than twice as many rising sequences as in the preceding shuffle, and this is true no matter how many cards you use, be it eight or eight million. As a result, the number of rising sequences is like a barometer that tells you how thoroughly a deck has been mixed.
So how many times on average do you need to shuffle a deck before the cards become truly random? This was the question that no one could answer before Diaconis and Bayer came along—and the one on which Jordan’s mystery hinged. Using cutting-edge probability and statistics, Diaconis and Bayer turned the seminal Bell Labs concept into a sophisticated new model, which Bayer then tested using computer simulations that shuffled virtual decks billions of times and analyzed the results.
What they found after a subsequent theoretical analysis came as a surprise. It took an average of seven shuffles to mix a deck—far more than anyone had anticipated. “The numbers were extremely compelling,” said Bayer. “It’s rare for empirical data.”*
When Bayer did his trick for us in class, he’d used a pack of playing cards in new deck order, so he knew the starting sequence of the cards. Because shuffling three times splices the deck into at most eight rising sequences, he was able to tell simply by looking through the deck which card was out of place.
To understand exactly how this works, consider a simplified version using our eight-card deck. The cards begin in sequential order: A 2
2 3
3 4
4 5
5 6
6 7
7 8
8 . The spectator shuffles once, picks a card at random, and replaces it at a different position. The magician then examines the cards and finds them in, say, the following configuration: 5
. The spectator shuffles once, picks a card at random, and replaces it at a different position. The magician then examines the cards and finds them in, say, the following configuration: 5 6
6 A
A 7
7 3
3 8
8 4
4 2
2 . Can you tell which card was picked? Clearly the two is out of place, because the two should always come before the three, not after. Ergo, it’s the two of spades.
. Can you tell which card was picked? Clearly the two is out of place, because the two should always come before the three, not after. Ergo, it’s the two of spades.
Charles Jordan, the magician who posted the ad in the Sphinx, had stumbled upon this principle nearly a hundred years ago, and exploited it in his miracle by mail. The Jordan trick is slightly different, because the magician only looks at half the deck, but this is the main thrust of it. Either one card is found to be out of sequence or one card in the sequence is missing, depending on which half of the deck is mailed back to the magician.
Before Bayer and Diaconis published their results, shuffling three or four times before a game was the industry standard at the world’s top casinos, even for high rollers. Nobody ever doubted that this was adequate. With their work, the two mathematicians had uncovered a massive breach in casino security.
In the early days of card counting, when single-deck blackjack games were common in Nevada, and shuffling was far from thorough, it was relatively easy to gain an advantage over the house and claim big payouts. Indeed, the first few generations of card counters made millions. “It was basically like fishing in Newfoundland at that point,” said Bayer. “You could just clean up on single-deck hands in Las Vegas.”
Shortly after the shuffling paper appeared in print, Bayer was approached by an attorney representing a group of professional gamblers facing indictment for cheating at blackjack in Atlantic City. As an expert witness, Bayer was hired to build a defense pinned on the fact that the crew’s dubious winnings could be credited to shoddy shuffles and so-called card sequencing—that is, remembering unmixed strings of cards—rather than outright cheating. Bayer proved that you could legally beat the house by exploiting a persistent lack of randomness in the cards—the result of too few shuffles. In theory, this bit of exculpatory evidence should have been enough to exonerate the crew, but the case was settled out of court and never went to trial.
More striking even than the number of shuffles required to randomize a deck of cards is the way in which the cards become mixed. Rather than being an incremental process, with the amount of randomness gradually increasing, shuffling turns out to be highly nonlinear. Think of water freezing. As the ambient temperature drops, the water gets colder, but it remains a liquid—at ten degrees, at one degree, even at one-millionth of a degree Celsius—until the mercury hits zero, and then, presto! Water becomes ice.
In the same fashion, there’s little appreciable difference between one shuffle and five shuffles, or between seven shuffles and a hundred. Two shuffles aren’t twice as random as one, and four aren’t twice as good as two, as one might expect. Even after six shuffles, you can still pick out distinctly non-random patches. But right around the seventh shuffle—presto! The cards rapidly become mixed. The randomness suddenly congeals, and the deck undergoes what is known as a phase transition.
If you graph the amount of order, or information, in the deck against the number of shuffles, it looks like a steep cliff with a valley beneath it. Up until about the sixth shuffle it’s basically flat (the top of the cliff). Then, between six and seven shuffles, it drops off sharply (the cliff). After that it flatlines again (the valley). Seven shuffles is the tipping point, when the randomness snowballs and the deck decays exponentially into chaos.
As it turns out, this sort of nonlinear mixing occurs all over the place. When you knead bread dough, for instance, it smoothes out rather abruptly after a certain number of folds. Or, if you mix chocolate sauce into cake batter, you’ll see swirls of chocolate as you stir, and as you keep stirring, the swirls will suddenly disappear when the batter becomes uniformly mixed. After that, stirring doesn’t do much, except maybe ruin your batter, much as shuffling too many times wears out a deck.
Drug companies worry about this sort of thing all the time. Every batch of cold medicine, for example, needs to be suitably mixed, because you don’t want one person getting all the antihistamine while someone else is left with the analgesic. Overmixing, on the other hand, can denature the chemicals and ruin the batch, so it falls upon the company’s in-house Goldilocks, who might have a degree in statistics or chemical engineering, to determine the optimal mixing strategy.
“One can view all of reality as shaped by probability theory,” Bayer said to us at the end of his lecture. Indeed, what started out as a somewhat esoteric investigation into the statistical properties of an old magic trick led to a model for a widespread class of systems. “People knew this kind of cutoff phenomenon happened as a random process in lots of situations,” he said. “But there was never a single model that showed that it happened before this one.”
THE CONJURING ARTS RESEARCH CENTER, one of the world’s largest magic libraries, is found inside a colorless building on West Thirtieth Street, a few blocks from another magic landmark: Tannen’s. On my first visit, I wasn’t sure what to expect—a Masonic lintel, the Eye of Horus on an architrave, the Gryffindor lion—but it wasn’t like that at all. The directory listed a rug company and a few residences, nothing to suggest that behind these doors lay the ultimate repository of arcane magical knowledge.
I took the elevator to the fifth floor and found myself in a long, dark hall at the far end of which was a lone door. A few magic-themed posters on the walls reassured me I was in the right place. Moments later, the door swung open and I saw a young woman walking briskly toward me. “You must be Alex,” she said in a formal tone. “Right this way.”
Her name was Alexis and she was the head librarian. The Conjuring Arts Research Center is not a walk-in library. Appointments are required at least one week in advance, so they’d been expecting me. It’s also not a browsing library, so visitors must be supervised at all times.
I followed Alexis into a windowless salon decorated with heavy oak furniture, skulls, swoops of red velvet, display cases loaded with puzzles and magic props and handmade decks of cards and printing plates and original Houdini handcuffs and lock picks and diagrams of escapes, all surrounded by ceiling-high shelves loaded with books, some of which looked very old. This was it, I thought, magic’s Library of Alexandria.
After Bayer’s class, I’d decided I wanted to see the original issue of the Sphinx in which Charles Jordan’s mind-reading mystery had first appeared. The only place I knew of with archives going back that far was the Conjuring Arts Research Center. While I was here, I figured I might also spend some time contemplating the history and philosophy of magic—a pursuit Jeff McBride associates with the realm of the Sage. And maybe, just maybe, I’d chance upon some ancient secrets that would help me in the construction of my routine.
This is actually a fairly common tactic. Magicians are constantly digging up old material and passing it off as new. A number of David Blaine’s earliest effects, for instance, were tomb-raided from ancient texts. One of them was inspired by an Egyptian papyrus, housed at a museum in Berlin, that depicts the conjuror Djedi of Djed-Snefru ripping the head off a goose while pyramid-builder King Cheops looks on in awe. Djedi reattaches the head, and the bird waddles off. Forty-five hundred years later, David Blaine performed this same trick on his debut television special (except he used a chicken instead of a goose).
My motivation had been further reinforced by something gambling expert Jason England told me on one of my many trips to Vegas. “If you want to fool magicians,” he said, “you’re not going to fool them with a new move. You’re going to fool them with some hundred-year-old mathematical principle. Forget about the latest move. Go the other direction. Go dig up some ancient book.” He paused for a moment, and then added, “Go to the library.”
Rustico II regular Bob Friedhoffer shared this view, although he had a different way of putting it. “Learn the history,” he said to me one day. “I’m serious. Learn it or you’re dead to me.”
The Conjuring Arts Research Center houses roughly fifteen thousand books and magazines, along with rare unpublished manuscripts and letters and ephemera and scribal works dating back to the fifteenth century. There are more than a thousand volumes printed before 1900, and several hundred that predate the founding of our great nation. As my eyes fixed on a long shelf packed with books on math and magic, I wondered if perhaps my dream effect wasn’t hidden somewhere in those pages.
I wove in and out of the stacks, shadowed every step of the way by the ever-vigilant Alexis. Sweeping my gaze over the towering wall-to-wall shelves, I saw books on lying and psychology, conjuring theory, crowd manipulation, and puzzles. There was a shelf devoted to the history of playing cards, and an entire row of forcing books, which are props used to force words and phrases onto your spectators; manuals on coin tricks, escapes, ventriloquism, juggling, thaumaturgy, psychokinesis, and levitation. Strolling past the gambling section, I reached for a book on cheating at poker, and Alexis grabbed my wrist.
“Don’t touch it,” she said tartly. The books were fragile, she explained, and had to be handled carefully. “What do you need?”
I pointed sheepishly at the book, and she shimmied it off the shelf without touching the binding.
Alexis then led me into another, smaller room toward the rear of the library that contained, among other things, a number of declassified CIA documents. Back in the 1950s, during its kooky MK-ULTRA days, the CIA hired magician John Mulholland to train spies in the art of deception, an initiative predicated on the assumption that, as CIA deputy director and amateur magician John E. McLaughlin put it, “magic and espionage are really kindred arts.”
The man behind this remarkable collection was a deep-pocketed sleight-of-hand master and potato baron named William Kalush, who worked with David Blaine on a number of effects, including one in which Kalush fired a rifle bullet into Blaine’s mouth. Many of the items in the library were on semipermanent loan from Kalush’s private stash. Wealthy and well connected, Kalush was buddies with Blaine (who sat on the board) and card star Ricky Jay. Jay-Z, an acquaintance of Kalush and a magic fan, had donated the bookcases.
The library’s greatest treasures were kept in the rare book room, hidden in the back and protected by locks. I was not allowed to enter, but I’d heard this room housed an English book on microscopy with descriptions of water spouters, tricksters who regurgitate swallowed liquids; a Swedish cookbook from the 1700s with a section on postprandial magic tricks; a three-hundred-year-old Belgian legal text that explains various methods for cheating at dice; and an original edition of Reginald Scot’s 1584 Discoverie of Witchcraft. Inside this treasure room were secrets in Dutch, French, German, Italian, Japanese, Portuguese, Russian, Spanish, and Swedish. (The library employs a full-time translator, whose previous jobs included a stint as the official translator to Pope John Paul I.) A first edition of S. W. Erdnase’s 1902 The Expert at the Card Table was one of the newest items on the shelves. I felt faint.
HUNCHED OVER A SMALL TABLE in the library’s main salon, I contemplated the document Alexis had brought out for me. It seemed to glow in the soft yellow warmth of the reading lamp. The cover was printed in red Egyptian lettering with a drawing of the Sphinx at the top. It was dated May 1916. The Sphinx was quite possibly the most influential magic magazine of all time. Original copies are as valuable as they are rare. This was the first one I’d ever seen up close.
I peeled back the cover. The pages were foxed and faded and smelled faintly of must and mothballs and—I could have sworn—hair tonic. Inside were minutes of recent meetings, a roster of newly elected members, and other oddments. I scanned the first page.
The 156th regular monthly meeting was held at the Magical Palace, 493 Sixth Avenue, New York City, on Saturday . . . The Committee on Admissions reported as worthy the candidate whose application was received last month, and after being balloted for, was declared duly elected . . . The Mysteries were conferred in short form on E. D. Robinson of Rutland, Vermont, and he was well pleased with the ceremony . . . President Dick showed his improved 4-Ace trick and several other card creations keeping time with his left eyebrow, all of which pleased greatly.
Leafing through the magazine, I imagined a time when gentleman conjurors assembled in their very own meeting house, insulated from the rigors of city life, rather than being reduced to meeting at pizzerias and taco shops, hospitals, and veterans lodges. How the mighty had fallen.
I finally found what I was looking for on the third-to-last page. Buried among diagrams for apparatuses and props, directions for how to build a Die Box, and promotions for new effects was the most modest of ads:

Staring at Jordan’s ad, I fell to thinking about the unlikely paths that can lead to great discoveries. It struck me as rather poetic that this old trick had inspired a modern mathematical breakthrough, for some of the earliest recorded magic tricks appear in a fifteenth-century book written by a Tuscan mathematician who happened to be a close friend of Leonardo da Vinci’s and helped him paint The Last Supper. De viribus quantitatis (On the Power of Numbers) contains instructions on how to eat fire, wash your hands in molten lead, write on a rose petal, make a coin or an egg bounce up and down by forces unseen, and read minds using mentalism techniques still in use today. (Most of these tricks actually work, as Bill Kalush will tell you.) The book also has the first written accounts of card tricks. De viribus quantitatis was never published; it lay hidden in the University of Bologna archives for five hundred years before being brought to light by a British mathematician who stumbled across references to it in other works. Now the world’s only English translation was locked inside the CARC’s rare book room, a few feet from where I was sitting.
The library’s second-oldest volume is the medieval Latin pseudepigraphon The Book of Secrets of Albertus Magnus, one of the most popular works of the Middle Ages. In it, the author—probably one of St. Magnus’s students—describes hundreds of extraordinary properties of animals, herbs, and stones, some of which can be used to make magic. Among them is a method for resurrecting a drowned fly by burying it in ashes, which to a naïve audience looks like a miracle even today. The secret lies in the fact that insects breathe through tiny openings in their exoskeletons. Submerging a fly in water cuts off its oxygen supply, causing it to pass out. The ashes in turn dry it off, allowing the fly to breathe again, effecting an apparent resurrection. Thus, this trick doubles as an early entomological experiment.
The Book of Secrets belongs to a class of vernacular literature that was popular in Europe during the fifteenth century and endured well into the Elizabethan age. As Europe emerged from the Dark Ages and printing presses spread across the Continent, so-called books of secrets—bizarre medleys of magic, bestiary,* metallurgy, recipes, tinctures and elixirs, and some actual scientific facts—became commonplace. From our modern vantage point, it’s easy to dismiss most of this stuff as hokum. But empirical science was born out of these ungainly mash-ups.
Today we tend to view magic and science as polar opposites, with superstition at one end and rationality at the other. But this is a relatively recent distinction. For centuries, magic and science were widely seen as parallel paths to wisdom. Newton wrote more about the occult than any other subject, while toiling in secret over alchemical tracts that, had they been exposed, would have landed him in prison, because alchemy was deemed satanic by the Church. After his death, the Royal Society stashed away the embarrassing evidence, and for centuries these papers remained hidden, known only to a select few. Rediscovered in the mid-1900s, they reveal the striking extent to which Newton’s laws—the bedrock of physics—were shaped by theories of attraction and repulsion laid out in the alchemical cookbooks of his day. Gottfried Leibniz, coinventor of calculus, got his start as an alchemist in Nuremberg. Robert Boyle, founder of modern chemistry, spent half his life searching for the philosopher’s stone, the legendary substance that turns lead into gold. Jan Baptista van Helmont, the occult philosopher who laid out the first useful theory of gases in the early 1700s, did so through the prism of a profoundly mystical worldview. Practically every great thinker of the scientific revolution was interested in magic.
Technical curiosity and a penchant for tinkering continued to link science and magic during the nineteenth century, albeit in a more down-to-earth way. By and large the icons of nineteenth-century magic were Edisonian types who toyed with elaborate contraptions in private laboratories and studios. The father of modern magic, Jean-Eugène Robert-Houdin, was himself an accomplished scientist who conducted early experiments in electromagnetism and invented a number of devices for regulating electrical currents. (Beginning in the mid-eighteenth century, exhibitions of electromagnetic phenomena—which were variously billed as scientific experiments and spiritual manifestations—became a common feature of entertainment magic.) Robert-Houdin also built mechanical figures and automata, including a small android that he sold to P. T. Barnum. He designed the world’s first electric burglar alarm. His famous mechanical orange tree, which blossomed real fruit, is a classic of magical engineering. Using his knowledge of magic and physics, he once quashed a tribal rebellion in French Algeria by dazzling the local chieftains with his godlike powers—a mission for which he received a royal commendation.
An amateur magician and disciple of Robert-Houdin invented trick photography and created the first special-effects films. (Magic played a foundational role in the development and dissemination of movie technology.) Another nineteenth-century engineer, Henry Dircks, invented Pepper’s Ghost, an early theatrical illusion that inspired two of the most famous tales in Alice’s Adventures in Wonderland—the “Cheshire Cat” and “Pig and Pepper.” (An avid fan of magic, Lewis Carroll witnessed the illusion while attending a magic show with none other than Alice Liddell, the real-life inspiration for the Alice stories.) Other magicians invented the parachute, the first ribbonless typewriters, coin-op locks, and vending machines.
The tradition of the magician-scientist persisted even throughout much of recent history. Up until the late 1930s, magic shows were still being billed as scientific amusements or wonders of natural philosophy. And until just a few years ago, the Academy of Magical Arts, one of America’s three magic fraternities, was known as the Academy of Magical Arts and Sciences.
To the heroes of the scientific revolution, science and magic were kindred sources of wonder. More than five centuries after the first conjuring texts came into being, the art and science of magic are as vibrant and mysterious as ever. Meanwhile scientists of all stripes—be they psychologists, neurobiologists, or mathematicians—continue to look toward magic as a source of inspiration.
AS THE DAY OF THE IBM competition drew near, I began searching with ever-greater urgency for the perfect trick. My subway reading now consisted of obscure math articles, old Martin Gardner columns, books on probability and information theory I’d plucked from the math library. I managed to track down Gilbert’s original 1955 Bell Labs memo, which turned out to be as rare as issues of the Sphinx. It had never been published, and none of the dozen or so mathematicians I contacted—guys who, at one point or another, had all worked on the problem of shuffling—had ever seen a copy, including Bayer. After some serious gumshoeing, I finally located Gilbert himself. He was retired and lived in New Jersey. I reached out and touched him the old-fashioned way—by phone—and he kindly mailed me a copy.
I became a regular at Bayer’s office hours. I did card tricks for him and his grad students, which Bayer seemed to enjoy, although he did ask me on more than one occasion if I’d ever considered psychiatric treatment. Rumors began to spread of a crazy magician lurking in the halls of the math department. Walking into a symposium one afternoon, I saw Bayer nudge a professor sitting next to him and whisper, “That’s the magician.” Word traveled fast.
If Persi Diaconis is the coolest mathematician in the world, Bayer comes in a close second. A wisecracking, effervescent man of fifty-five who always wears jeans and frequently goes barefoot, with shaggy wisps of gray hair and curious green eyes, Bayer runs marathons, plays the ukulele, and climbs mountains in his spare time. In a field full of wallflowers—an extroverted mathematician, goes an old joke, is one who looks at your feet while he’s talking—Bayer is remarkably outgoing.
Listening to him talk is an exercise in mental agility, the intellectual equivalent of riding a mechanical bull. His thoughts buck and swerve and double back so quickly, often in mid-sentence, that it’s a struggle to stay on board. When he gave me a crash course on information theory, it began with a story about Grateful Dead bassist Phil Lesh. (It made perfect sense at the time, but I’d be hard-pressed to repeat it. Also, using a slide rule is apparently a lot like playing a fretless bass.) A system for cheating at blackjack turned into an indictment of Wall Street. Why can nobody match the NSA at code breaking? Why are there so few nuclear powers? Why did the Giants fall into a losing streak after seemingly sound trades? It was all connected by the formulas he scribbled on the board. Whenever he was deep in thought—like after I showed him my Ambitious Card routine—he swirled his tongue around in his mouth and puckered his lips as if sucking on a piece of candy.
In return for entertaining him, Bayer taught me about his research, dished about Russell Crowe, and regaled me with tales of Diaconis’s exploits. One of those stories was about a trick Bayer saw Diaconis perform at, of all places, a computer science conference. Strolling into a large lecture hall, where he was scheduled to give a talk, Diaconis whipped out a deck of cards and explained to the bemused audience that he was about to show them some magic. He wrapped a rubber band around the deck and threw it across the lecture hall. “He actually made a good shot,” Bayer remembers. “It landed on the middle of this table on the other side of the room.” (Bayer also recalls that the deck seemed oddly light.) The person nearest the deck gave it a cut, and five people took cards off the top. “If you have a red card, stand up,” Diaconis instructed them. Moments later, he named all five cards in order from across the room.
After baffling a roomful of computer scientists with this trick, he proceeded to baffle them further with an abstract lecture on something called the theory of finite fields. “This was deep modern algebra,” Bayer said. “I mean you can take an entire year of algebra, and minor in it, and not understand the talk. I didn’t, and I teach that course.”
The trick Bayer witnessed was a version of something known as the Tossed-out Deck, a classic of card mentalism wherein a deck is thrown into the audience, cards are selected, and the magician names the cards under seemingly impossible circumstances. It’s a nice effect because it engages multiple spectators, and the act of tossing the deck out into the crowd seems very fair, because of the distance it puts between the magician and the magic. As with the Ambitious Card and the cups and balls, many great magicians have tackled the Tossed-out Deck, and there are dozens of methods.
But pretty much every method has at least two flaws. First, the deck won’t stand up to close examination, unless you switch decks after the fact. Second, the magician usually needs to fish for clues in order to zero in on the cards. (“I sense a high card. Is it a seven or above? Is it an odd card?”) In capable hands, these are minor issues, but they are flaws nonetheless.
Diaconis’s version was pristine. Aside from being a little light, the deck was ungaffed, meaning there were no repeating banks of cards or marks on the backs. Furthermore, there was no fishing. Diaconis didn’t ask a single question before naming all five cards. He merely instructed the people with red cards to stand up. How could he have learned the identity of all five cards from this information alone? It was too good to be true. If I could learn this trick, I’d be a god among men. Or at least a man among little kids.
The secret, it turned out, was rooted in an obscure mathematical principle known as a De Bruijn sequence, after Dutch mathematician Nicolaas Govert de Bruijn. A De Bruijn sequence is a sequence of characters—letters or numbers or what have you—in which every possible subsequence of a given length appears once and only once. Consider, for example, the following string of eight letters: RRRBRBBB. This is a binary De Bruijn sequence of order 3. Binary means that the “alphabet” from which the sequence is composed contains only two elements (R and B), and it’s of order 3 because every possible three-letter subsequence—RRR, RRB, RBR, BRB, RBB, BBB, BBR, BRR—appears once and only once. For instance, the three-letter subsequence RBR, which starts on the third letter of the string and ends on the fifth, doesn’t appear anywhere else in the sequence.
This particular sequence is also said to be cyclic, because when you get to the far right end, you loop back around to the far left, as if you were hitting the carriage return on a typewriter. In other words, the subsequence BRR starts with the last letter on the right (B), continues at the far left (R), and ends on the second letter from the left (R). It helps to picture a circle:
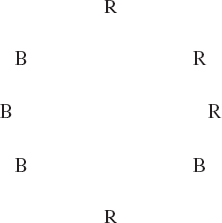
The oldest-known De Bruijn sequence appears in Sanskrit, in a 3,000-year-old fragment of Vedic poetry. These days, engineers use De Bruijn sequences to build smarter robots, neuroscientists use them to study how the brain encodes a stream of sensory input, programmers apply them to game design, and cybercriminals use them to hack open electronic locks protected by numerical key codes like those found on many luxury cars.
The De Bruijn sequence can also be weaponized to create mind-blowing magic. To see how, imagine that R stands for a red card and B for a black card and that I have a packet of eight cards in the following order: Q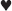 , 3
, 3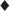 , A
, A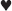 , 4
, 4 , 2
, 2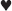 , 3
, 3 , 2
, 2 , 7
, 7 . This corresponds to the color sequence shown in the circle, with the queen of hearts at twelve o’clock. Now, let’s say I remove three consecutive cards from somewhere in this eight-card packet. All I need to tell you is the color sequence, and you’ll know what cards I’ve taken. If, for example, I tell you that the colors are red, black, red, you know immediately that the three cards I’ve selected are A
. This corresponds to the color sequence shown in the circle, with the queen of hearts at twelve o’clock. Now, let’s say I remove three consecutive cards from somewhere in this eight-card packet. All I need to tell you is the color sequence, and you’ll know what cards I’ve taken. If, for example, I tell you that the colors are red, black, red, you know immediately that the three cards I’ve selected are A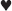 , 4
, 4 , and 2
, and 2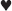 , because that’s the only sequence of red, black, red in the string. And because the sequence is cyclic, the deck can be cut as many times as you like. All cutting does is change the starting point on the circle.
, because that’s the only sequence of red, black, red in the string. And because the sequence is cyclic, the deck can be cut as many times as you like. All cutting does is change the starting point on the circle.
With only eight cards it’s not a very strong trick, but imagine doing it with lots of cards. Persi Diaconis used a thirty-two-card packet, hence the “light deck” Bayer had observed. It was still amazing, but I decided I wanted to take it to the next level and do it with a full regulation deck, one that could be freely examined. Evidently, nobody had ever done this before. Which meant that if I cracked the code to this one effect, I’d be the only person in the world able to perform it.
I teamed up with a grad student I met through Bayer, a woman named Nava, who was also interested in magic, and we wrote a computer program to find a suitable fifty-two-card sequence. Then I arranged a deck of cards in order according to this color pattern. Next I had to memorize the order of the cards. If this sounds like a lot of memorization, that’s because it is. The trick is mentally demanding, but that’s the price you pay for such a perfect trick. (As magicians like to say, every miracle has a price.) It also has the virtue of its defect, because this complexity helps disguise the method. Even if someone were to figure out the underlying principle—and that’s a stretch—most people would probably have a hard time imagining that anyone could commit so much information to memory. Maybe this is why magicians have been using stacked decks and mnemonic systems since the sixteenth century. As Jamy Ian Swiss aptly put it, “One of the best-kept secrets we have as magicians is that laymen would never imagine we would work so hard to fool them.”
Even had I not smoked a lot of pot in college, memorizing this much information without some kind of cognitive aid would have been daunting, so I consulted former U.S.A. Memory Champion Joshua Foer, an expert on mnemonics and author of the book Moonwalking with Einstein. He taught me an amazing technique, called the method of loci, which can endow even the wimpiest brain with superhuman powers of recall. The technique works by tapping into the near-limitless depths of spatial memory. Contrary to popular belief, photographic memory is not solely the province of savants. Everyone has a photographic memory. Most people just don’t know how to access it. The method of loci takes you there.
The basic idea is to store memories as images inside an imaginary space known as a memory palace. To memorize a deck of cards, for example, you first associate each card with an image—usually a person, object, or action. I chose to use people. The four of clubs, for instance, was Penn Jillette. (I made all the fours magicians.) The five of diamonds was Richard Feynman. (Fives were scientists.) The eight of clubs was Shaquille O’Neal. (Eights were athletes.)
After assigning an image to each card, you install the images at different points (or loci) along a predetermined path through your memory palace. Any kind of place will work, although it’s best to use one that’s familiar to you, such as your home or office. I chose the house I grew up in. You also want to pick a route that’s easy to retrace. I decided to follow the left wall, from the entryway to the dining room, through the kitchen, and into my parents’ bedroom, then into the living room, my dad’s study, my bedroom, and finally the garage.
By placing the images in your memory palace, you’re effectively encoding the order of the cards as a set of spatial relationships inside your mind. Later on, when you want to remember them, you simply retrace your steps through this virtual world. Strange as it may seem, the images appear in your mind almost effortlessly. The system is also remarkably robust. Once the images are fixed in your memory palace, they tend to stay there until you consciously evict them.
It may sound like a lot of work—why memorize more than you need to?—but the counterintuitive thing about memory is that more is often easier to remember than less. Memory is largely an associative process, and the more associations you make—particularly visual ones—the easier it is for memories to gain traction in your brain.
Once you’ve done the necessary spadework, committing a deck to memory is a breeze. It took me, a total novice, the lesser part of an evening. The world’s top mnemonists can memorize shuffled decks in under a minute. The current world record is 21.9 seconds—less time than it takes most people to deal out 52 cards. And it doesn’t work just for cards, either. The same strategy can be applied to words, letters, numbers—anything. In 2006 the World Memory Champion used it to memorize a string of 1,040 random digits in half an hour. Another well-adjusted individual has filled his memory palace with the first 65,536 digits of pi.
In addition to memorizing the order of the cards, I also had to know which color sequence each group of cards corresponded to. In the eight-card example just given, for instance, you need to know that red, black, red corresponds to A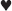 , 4
, 4 , 2
, 2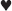 . The best way to remember this is to convert the subsequence red, black, red into a number (using a binary code), and then install that number inside your memory palace next to the first card in the group (in this case the A
. The best way to remember this is to convert the subsequence red, black, red into a number (using a binary code), and then install that number inside your memory palace next to the first card in the group (in this case the A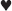 ). The number effectively tells you where in your memory palace to look.
). The number effectively tells you where in your memory palace to look.
To memorize the numbers, I used another memory trick called the Major System, which turns numbers into words. The number 36, for instance, became the word mash, because in the Major System, 3 = m and 6 = sh. (You fill in the vowels yourself.) After I turned all the numbers into words, I partnered them with the cards to form new images. For example, the four of clubs, together with the number 36, became an image of Penn Jillette (4 ) watching the show M.A.S.H. (36).
) watching the show M.A.S.H. (36).
Blame it on human nature, but it’s a well-known fact that our brains privilege lurid memories above more mundane ones. With this in mind, and following in the footsteps of champion mnemonists like Foer, I turned my memory palace into the set of a Pasolini film. In the entryway, David Duchovny (2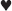 ) is consuming his own excrement (9 = poo). Physicist Richard Feynman (5
) is consuming his own excrement (9 = poo). Physicist Richard Feynman (5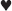 ) is puffing a doobie (19) at the kitchen table. Tom Cruise (10
) is puffing a doobie (19) at the kitchen table. Tom Cruise (10 ) is bleeding to death from a knife (28) wound inside the garage. Unspeakable acts are afoot in the linen closet. By the end of my virtual journey, I’d desecrated my childhood home. It was like that time during my senior year when my parents went on vacation and left me in charge for the weekend.
) is bleeding to death from a knife (28) wound inside the garage. Unspeakable acts are afoot in the linen closet. By the end of my virtual journey, I’d desecrated my childhood home. It was like that time during my senior year when my parents went on vacation and left me in charge for the weekend.
Once I had the trick down, it looked like this. A mixed deck of fifty-two cards is tossed into the audience. The person nearest the deck cuts as many times as they like, and six* people take cards off the top. “Should I do the red cards first or the black cards first?” I ask, casually. Of course, it doesn’t matter. “All right, if you have a black card, please stand up.” As soon I see the color configuration, I know all.
I want to put as much psychic distance as possible between the moment when I actually learn the identity of the cards—that is, when the people with black cards stand up—and the climax, when I call out all six cards. If I name the cards right away, it suggests a link between the color sequence and the cards. So I add some misdirection by tossing out a few silly, irrelevant questions. “What’s your sign?” I ask, pointing to one of my volunteers. This gets a laugh about half the time. I turn to another volunteer. “Did you have a pet growing up?” I single out a male spectator: “Boxers or briefs?”
In every great magic trick, form follows function. This silly bit spotlights the fact that I’m clearly not fishing for clues, while at the same time diverting attention away from the secret—all of which prevents people from connecting the dots. Once I’ve asked a few dumb questions, I tell everyone who has a card to stand up. Then I name all the cards in order, pointing at each person as I go down the line like a crack shot taking target practice.
All bull’s-eyes.
THIS EFFECT WAS A DUPER’S dream. The method was elegant. The impact was strong. It scored with muggles and magicians alike. It became my go-to trick for when I needed to fry a fellow member of the guild. I fooled some of the smartest magicians in New York City with it—the old guys at the pizzeria, the local president of the IBM, the regulars at Tannen’s and Fantasma. It was conjuror’s kryptonite. No one had a clue. Of course, this sent a tsunami of duping delight gushing through my veins. Jason England had been right. “If you want to fool magicians,” he’d said, “you’re going to fool them with some hundred-year-old mathematical principle.” His words echoed in my mind like a prophecy.
My weapon of math destruction was so well received (and so puzzled over) that Joshua Jay, an editor at Magic magazine and a virtuoso magician, offered to publish it in his monthly column. My invention would be forever enshrined in the world’s most widely read magic journal, alongside the works of Vernon and Houdini and Marlo and Tamariz and Wes James. I had yet to publish a single paper in a scientific journal, but I’d somehow managed to pull off an analogous feat in magic. Life, I suppose, has a way of playing tricks on you.
TO A MAN WITH A hammer, the whole world looks like a nail. Unable to think about anything but shuffling, math, and magic, I became convinced that the secrets of the universe were found inside a pack of playing cards.
For starters, there’s a curious symbolism encoded in a deck of cards. There are two colors (red and black) symbolizing day and night; four suits—spades, hearts, clubs, and diamonds—one for each season (or seasons of the magician's life cycle, if you like). The twelve court cards correspond to the months of the Gregorian calendar. Each suit contains thirteen cards, for the thirteen lunar cycles. There are fifty-two cards in a deck, those being the fifty-two weeks in a year. And if you add up the values of all 52 cards, including the joker, you get exactly 365. Add to this the seven shuffles and the surprising reach of the Bayer-Diaconis model—how shuffling mimics the behavior of everything from kneading dough to mixing chemicals—and cards really do start to look like cosmic instruments.
It goes even deeper when one considers the properties of a perfect, or faro, shuffle. Bayer and Diaconis got their result using a mechanical model for the messy, imprecise way people normally shuffle. The cards aren’t cut exactly in half, they’re riffled together haphazardly, and so forth. As it turns out, a certain measure of sloppiness is the essence of a good shuffle. Only through imprecision does randomness sluice through and accumulate, eventually drowning out the order completely.
A faro shuffle on the other hand—whereby the cards are divided exactly in half and perfectly interwoven—isn’t random at all. In fact, it’s completely predictable. Eight perfect shuffles will return a fifty-two-card deck to its original order, with every card having cycled back to its starting position. And it doesn’t just work for 52 cards. A deck of any size will eventually return to its starting order after a finite sequence of faro shuffles, although eight isn’t always the magic number.
One can derive a general formula for the relationship between the number of cards in the deck and the number of faro shuffles needed to complete one full cycle. The correlation, it turns out, is far from intuitive. If you have 25 cards, for instance, it takes 20 faros to reset the deck whereas for 32 cards it only takes 5. You have to faro a 104-card deck 51 times to return it to its original order, but only 36 faros are needed if you have 1,000 cards. With a million cards, the number of faro shuffles in one cycle jumps to 180, and for a billion it spikes to 667,332.
An intimidating sleight, the faro shuffle is often called the holy grail of card magic. (Of course there are lots of holy grails, depending on whom you ask.) For over a century it existed primarily as a concept, a theoretical construct, poorly understood. No one could execute the move, and a plurality of magicians deemed it impossible. It was the four-minute mile of magic. The looping nature of the faro was known, theoretically speaking, going back to the early 1900s, and there are references in Erdnase to “faro belts,” but these early treatments are peppered with errors.
The watershed really came in the 1950s, with the work of Chicago card expert Edward Marlo and British computer scientist Alex Elmsley. Elmsley was the first to write down the general formula for the faro. By experimenting with the move, he also uncovered a number of interesting applications, including a procedure for moving a card to any position in the deck, using a sequence of perfect shuffles. (The procedure brought to light a deep connection between the faro shuffle and the binary number system, the universal language of modern computing.)
The remarkable looping property of the faro shuffle is a facet of group theory. Loosely speaking, group theory is the mathematical language of symmetry. This is important because, from the top down, nature loves symmetry almost as much as she abhors a vacuum. Group theory has applications to biology, chemistry, and most notably, physics, where it provides the mathematical framework for the Standard Model—the overarching theory of elementary particles and forces that explains virtually every known natural phenomenon.
So, in a sense, a deck of cards really does contain the secrets of the universe.
The method most commonly used for the faro is to do it in your hands, rather than on a table. First you divide the deck exactly in half. (This takes practice.) Then you butt the short edges together under pressure, while keeping the two halves square, and gently work the cards into an alternating weave.
Technique has progressed a great deal in the last fifty years, and though it’s still considered an advanced move, the faro is now fairly common among sleight-of-hand junkies. A small number of people—maybe a hundred or so—can do it one-handed. Smaller still are the ranks of those who have mastered the table faro, by any measure the hardest move in all of close-up magic. A heroic sleight, the table faro is done not in the hands but on a flat surface. This posture affords far less control over the cards, making it a veritable leap of faith. Only a handful of people in the world can do it—blind cardsharp Richard Turner being one of them. (He does it in just over a second.) Turner can also do what is informally known as a volitional faro. This is when, instead of being butted together, the two halves are actually riffled together, with the thumbs alternately releasing the cards—one from the left, one from the right, and so on—until all 52 are interlaced. Turner can shuffle an entire deck this way in 8.1 seconds. “If you think this is easy,” notes veteran sleight-of-hand expert Jon Racherbaumer, “try making love while standing up in a hammock while juggling seven ice-cream cones.”
The regular in-the-hands faro is a subtle, knacky move, but far from impossible, provided you’re willing to sacrifice a large chunk of your social life. After being intimate with cards for so long that they began to feel like an extra appendage, I eventually saw the day arrive when, to my astonishment, I could faro a deck with remarkable consistency.
To get to the point where I could bang out eight perfect faros in a row under fire took a lot of practice. In the time I spent acquiring this skill, I could’ve learned French. But French is spoken only in a few pockets of the world. Magic is a universal language. Not only that, but French wouldn’t have brought me any nearer to mastering one of the greatest card effects of all time—the trick that would become my closer.
PICTURE THIS. A SURPRISINGLY HANDSOME magician asks a volunteer to write down the name of someone they know and fold up the paper without revealing the name to anyone. The magician tears up the paper and attempts to draw the face of the person with a black magic marker on a large sketchpad. After two unsuccessful but hilarious tries—first he draws a happy face, then a sad face—he produces a deck of cards and removes them from the box. On the edges of the deck are a number of randomly scattered blue markings. He fans the cards to show that they are mixed.
“The dots are like an inkblot test,” he explains. “They can become whatever it is your imagination projects onto them.” He then asks the volunteer to select a card and return it to the pack.
The deck is shuffled and, as if by the action of some mysterious force, the dots begin to form a pattern, visibly organizing themselves into the name of the card the volunteer selected.
But wait. It gets better.
“I now want you to focus all your mental energy on the name you wrote down,” he says, fixing his volunteer with a serious look. “This is someone who means a lot to you, isn’t it? Someone who has played an important role in your life?”
The spectator nods.
“And you haven’t told anyone who it is.”
Looking over the anxious faces of the audience, the magician shuffles one last time—for a total of eight shuffles in all, but who’s counting—and, like a picture emerging from static, the dots rearrange themselves into the name that the volunteer secretly wrote down at the beginning of the trick.
There are very few genuine miracles in this world: childbirth, the Big Bang, John Bonham’s kick drum on “Good Times, Bad Times,” Joe DiMaggio’s fifty-six-game hitting streak.
And this . . .
It came to me like a hallucination, in one feverish evening. I saw it fully formed, like chemist August Kekulé’s famous vision of the benzene ring. Together with my Tossed-out Deck, I now had two amazing effects, worth a solid ten minutes of jaw-dropping magic. Both exploited elegant mathematical principles. Both had a mentalism angle. Both drew heavily on the skills I’d acquired along the way—the center tear, cold reading, false shuffles, the faro—a tour de force of deception. My routine was complete.
I had found my tricks.
* It’s also rare to get such a magical number, symbolically speaking. Seven is the granddaddy of sacred numbers, as ancient as history. In the Bible there are seven days of creation, seven virtues, seven deadly sins, seven pillars of wisdom, seven sorrows (and joys) of the Virgin, seven divisions of the Lord’s Prayer, seven sacraments, seven cardinal sins, and seven graces. The Book of Revelations, the last chapter of the New Testament, is built around the number seven. It speaks of seven trumpets (heralding the end of days), seven golden lamp stands (representing the seven churches of the apocalypse), seven golden stars (representing the seven angels of the apocalypse), seven spirits before the throne of God, seven plagues, seven bowls of wrath, seven vials, seven judgments, seven kings, a seven-headed beast, a dragon with seven heads wearing seven diadems, a lamb with seven eyes, and an earthquake that kills seven thousand people.
The three most important Jewish feasts each lasts seven days, as do Levitical purifications, and the sabbatical occurs every seven years. Ancient astrologers recognized seven planets. In Islam, there are seven heavens, the seventh being by far the most paradisiacal, and seven holy sleepers (as is also true in Roman martyrdom). Buddhists revere the seven treasures. In many religions, the seventh son of a seventh son is endowed with magical powers. Japanese folklore has seven gods of good fortune. Inanna, the most powerful goddess in Sumerian folklore, passes through seven gates on her journey through the underworld.
There are seven days in a week, seven seas, seven continents, seven dwarves, seven wonders of the ancient world, seven Police Academy movies, seven whole notes in a Western scale, and seven words, as per George Carlin, that you can’t say on TV. Shakespeare famously wrote of the seven ages of man. The average number of objects a human being can retain in short-term memory is seven. (This is why phone numbers have seven digits). Seven is the most likely roll in craps, and the opposite sides of a dice always add to seven. Se7en was Brad Pitt’s best film, and Seven of Nine, portrayed by actress Jeri Ryan, was incontrovertibly the hottest girl ever to appear on Star Trek.
* No, not bestiality, but bestiary, as in a collection of facts about beasts.
* In an eight-card De Bruijn deck, the smallest unique subsequence is three cards long, but with fifty-two cards, the smallest unique subsequence is six cards long, for reasons I won’t go into. This is why six cards are selected.