CHAPTER 8
Parallelograms and Other Polygons
The study of triangles and their relationships provides a tool for investigating other figures: quadrilaterals of various types and polygons with more than four sides. All that you’ve learned about congruence will be used again and again.
Parallelograms
A parallelogram is a quadrilateral with two pairs of opposite sides parallel. If you focus on one pair of parallel lines and view the other lines as transversals, you can show that consecutive interior angles are supplementary:
 Consecutive angles of a parallelogram are supplementary.
Consecutive angles of a parallelogram are supplementary.
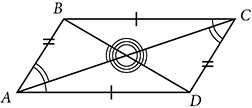
Drawing a diagonal in a parallelogram divides it into two triangles that can easily be shown to be congruent. By CPCTC, it can be proven that every parallelogram has these properties:
 Opposite sides of a parallelogram are congruent.
Opposite sides of a parallelogram are congruent.
 Opposite angles of a parallelogram are congruent.
Opposite angles of a parallelogram are congruent.
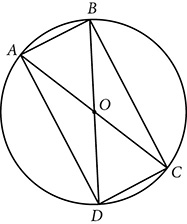
If both diagonals are drawn, proving congruent triangles and showing corresponding parts are congruent will let you show:
 The diagonals of a parallelogram bisect each other.
The diagonals of a parallelogram bisect each other.
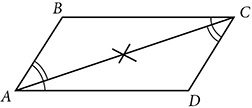
To prove that a quadrilateral is a parallelogram, you need to prove one of the following:
 Both pairs of opposite sides are parallel.
Both pairs of opposite sides are parallel.
 Both pairs of opposite sides are congruent.
Both pairs of opposite sides are congruent.
 One pair of opposite sides is both parallel and congruent.
One pair of opposite sides is both parallel and congruent.
 Both pairs of opposite angles are congruent.
Both pairs of opposite angles are congruent.
 Diagonals bisect one another.
Diagonals bisect one another.
The area of a parallelogram is equal to the length of the base times the height, or perpendicular distance between the parallel sides. (A = bh)
EXAMPLE
Rectangles, Rhombuses, and Squares
A rectangle is a parallelogram with a right angle. Because every rectangle is a parallelogram, it has all the properties of a parallelogram. Because opposite angles are congruent and consecutive angles are supplementary, all four angles in a rectangle are right angles. It is also possible to show that the diagonals of a rectangle are congruent.
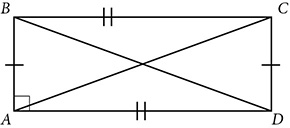
EXAMPLE
A rhombus is a parallelogram with four sides of equal length. It is a parallelogram, so has all the properties of a parallelogram, including opposite angles congruent and consecutive angles supplementary, but may not have all angles congruent. The diagonals of a rhombus intersect at right angles and bisect the interior angles.

A square is a parallelogram that is both a rectangle and a rhombus. A square has four congruent sides and four right angles. It has all the properties of a parallelogram, as well as the properties of rectangles and rhombuses. Because a square is both equilateral and equiangular, it is a regular polygon.
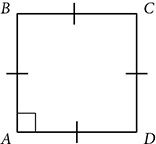
To prove that a quadrilateral is a rectangle or rhombus or square, you must first prove that it is a parallelogram. Once that is established, you need to prove an additional property to classify the parallelogram further.
Rectangle |
Prove one angle is a right angle, or prove diagonals are congruent. |
Rhombus |
Prove adjacent sides congruent, or prove diagonals are perpendicular or prove the diagonals bisect interior angles. |
Square |
Prove that the parallelogram is both a rectangle and a rhombus. |
The area of a rectangle, like any parallelogram, is A = bh but in a rectangle, the base and height are adjacent sides. The area of a square is also A = bh, but since the square is a rectangle with sides of equal length, that formula becomes A = bh = s ⋅ s = s2. The area of a rhombus can be found as A = bh but can also be found from the lengths of the diagonals. Drawing both diagonals, d1 and d2, creates four right triangles, and each right triangle has legs that measure 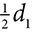 and
and 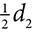 . The area of each of those right triangles is
. The area of each of those right triangles is  . There are four right triangles making up the rhombus, so the area of the rhombus is
. There are four right triangles making up the rhombus, so the area of the rhombus is 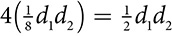 .
.
EXAMPLE
Trapezoids
A trapezoid is a quadrilateral with one pair of parallel sides. The parallel sides, usually referred to as the bases, are of different lengths. The nonparallel sides, sometimes called legs, may be different lengths or the same length. A trapezoid in which the nonparallel sides are congruent is an isosceles trapezoid.
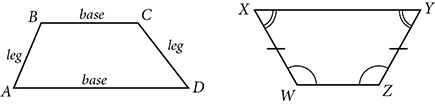
In a trapezoid, the pair of angles at each end of one of the parallel sides is a pair of base angles. In an isosceles trapezoid, a pair of base angles has the same measure. This is not true if the trapezoid is not isosceles. In any trapezoid, the consecutive angles between the parallel sides, along one leg, are supplementary.

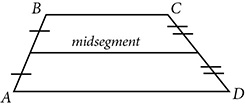
The line segment that connects the midpoints of the nonparallel sides of a trapezoid is the midsegment. The midsegment of a trapezoid is parallel to the bases and equal in length to the average of the two bases.
The area of a trapezoid is  , where b1 and b2 are the lengths of the two parallel sides and h is the perpendicular distance between the parallel sides. You may notice that
, where b1 and b2 are the lengths of the two parallel sides and h is the perpendicular distance between the parallel sides. You may notice that 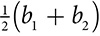 within that formula is the average of the bases, and so the length of the midsegment. The area of a trapezoid is the length of the midsegment times the height.
within that formula is the average of the bases, and so the length of the midsegment. The area of a trapezoid is the length of the midsegment times the height.
EXAMPLE
Regular Polygons
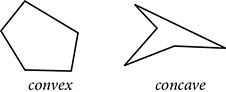
A polygon is any closed figure made of line segments that intersect only at their endpoints. A polygon is convex if any diagonal falls inside the polygon. A polygon that is not convex is concave. Concave polygons “cave in,” or have dents in them.
Polygons are named by number of sides:
3 → triangle
4 → quadrilateral
5 → pentagon
6 → hexagon
7 → heptagon
8 → octagon
9 → nonagon
10 → decagon
12 → dodecagon
A convex polygon is regular if it is both equilateral and equiangular. An equilateral triangle is a regular three-sided polygon because it has three congruent sides and three angles of equal size. Remember a rectangle is equiangular but not equilateral, and a rhombus is equilateral but not equiangular. Only a square is a regular quadrilateral.
Using the construction skills you have learned, it is possible to construct several different regular polygons. These constructions inscribe the regular polygon in a circle, creating the polygon with each of its vertices on a circle.
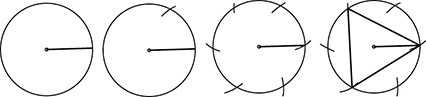
 Construct a regular hexagon inscribed in a circle. Draw a radius, connecting the center to any point on the circle. Set the compass opening to the length of the radius of the circle. Place the point of the circle at the point at which the radius meets the circle. Scribe an arc that intersects the circle. Move the point of the compass to the point where the arc crosses the circle, and scribe another arc. Repeat until you return to your starting point. This divides the circle into six congruent arcs. Draw line segments connecting these points in sequence around the circle to create a regular hexagon.
Construct a regular hexagon inscribed in a circle. Draw a radius, connecting the center to any point on the circle. Set the compass opening to the length of the radius of the circle. Place the point of the circle at the point at which the radius meets the circle. Scribe an arc that intersects the circle. Move the point of the compass to the point where the arc crosses the circle, and scribe another arc. Repeat until you return to your starting point. This divides the circle into six congruent arcs. Draw line segments connecting these points in sequence around the circle to create a regular hexagon.
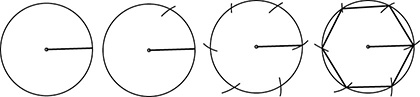
 Construct an equilateral triangle inscribed in a circle. Begin as for a regular hexagon, dividing the circle into six congruent arcs. Draw line segments connecting every other point around the circle to create an equilateral triangle.
Construct an equilateral triangle inscribed in a circle. Begin as for a regular hexagon, dividing the circle into six congruent arcs. Draw line segments connecting every other point around the circle to create an equilateral triangle.
 Construct a square inscribed in a circle. If the center of the circle is marked, draw a line through the center, intersecting the circle in two points, to create a diameter.
Construct a square inscribed in a circle. If the center of the circle is marked, draw a line through the center, intersecting the circle in two points, to create a diameter.
If the center is not marked, construct a right angle with its vertex on the circle by first drawing a line that intersects the circle in two places and then constructing a perpendicular to the line at one of the points where it intersects the circle. Connect the points where the sides of this right angle intersect the circle. That produces a diameter.
Whichever method you used to get a diameter, construct the perpendicular bisector of your diameter to create a second diameter, perpendicular to the first. The points at which these diameters intersect the circle divide it into four congruent arcs. Connect those points with line segments to create a square.
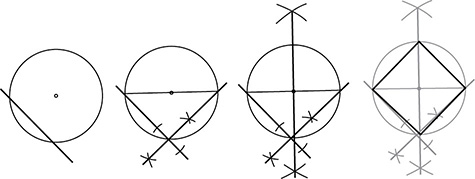
Angles of Regular Polygons
Like triangles and quadrilaterals, polygons with more than four sides have as many vertices and interior angles as sides. Each vertex is connected to two other adjacent vertices by sides. By drawing diagonals from a vertex to each of the non-adjacent vertices, you can divide a convex polygon into n − 2 nonoverlapping triangles. The sum of the measures of the interior angles of those triangles is equal to the sum of the measures of the interior angles of the polygon.
In the figure below, m∠A + m∠B + m∠C + m∠D + m∠E = (m∠1 + m∠5) + (m∠2) + (m∠3 + m∠4 + m∠8) + (m∠9) + (m∠6 + m∠7) = (m∠1 + m∠2 + m∠3) + (m∠4 + m∠5 + m∠6) + (m∠7 + m∠8 + m∠9). Each triangle has angles that total 180°, so m∠A + m∠B + m∠C + m∠D + m∠E = 3(180°).
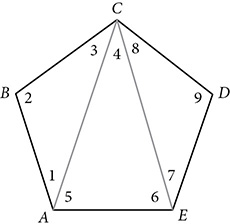
 A convex polygon of n sides has n interior angles whose measures add to 180(n − 2)°.
A convex polygon of n sides has n interior angles whose measures add to 180(n − 2)°.
 If the polygon is regular, the measure of each interior angle is
If the polygon is regular, the measure of each interior angle is  .
.
If one side of the polygon is extended through a vertex, an exterior angle is formed. Each exterior angle is supplementary to the interior angle at that vertex. If one exterior angle is created at each vertex, the sum of their measures is equal to:
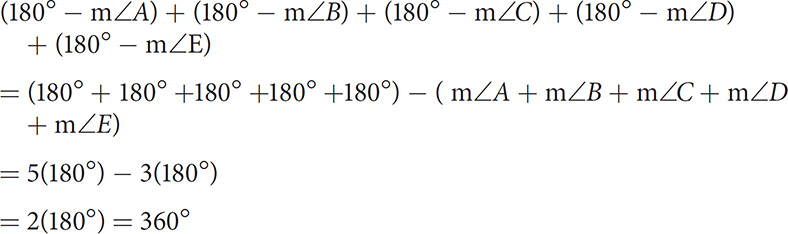
 The sum of the exterior angles (one at each vertex) of any convex polygon is 360°.
The sum of the exterior angles (one at each vertex) of any convex polygon is 360°.
 If the polygon is regular with n sides, each exterior angle measures
If the polygon is regular with n sides, each exterior angle measures 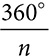 .
.
A segment drawn from the center of a regular polygon to a vertex is a radius. When radii are drawn to two adjacent vertices, they form a central angle. A regular polygon with n sides has n central angles, and the measure of each is 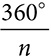 . Drawing all n radii divides the regular polygon into n isosceles triangles. Each triangle has a central angle as its vertex angle, and each of its base angles are half of an interior angle of the regular polygon.
. Drawing all n radii divides the regular polygon into n isosceles triangles. Each triangle has a central angle as its vertex angle, and each of its base angles are half of an interior angle of the regular polygon.

Areas of Regular Polygons
The area of a convex polygon with more than four sides can sometimes be found by breaking it into nonoverlapping triangles, finding the area of each, and summing the results. With regular polygons, this can be accomplished by drawing segments, called radii, from the center of the regular polygon to each vertex. In a regular polygon with n sides, this creates n congruent isosceles triangles. If you can find the area of one of these, multiplying by the number of sides will give you the area of the regular polygon.
The formula for the area of a regular polygon is a simplified rule for that process. The area of one triangle is 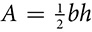 , with b equal to one side of the polygon and h equal to the height or altitude of the small isosceles triangle. That height is called the apothem of the regular polygon. The area of the regular polygon with n sides is
, with b equal to one side of the polygon and h equal to the height or altitude of the small isosceles triangle. That height is called the apothem of the regular polygon. The area of the regular polygon with n sides is 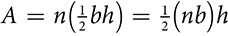 . Because nb is the perimeter of the regular polygon and h is the apothem, that formula can be represented as
. Because nb is the perimeter of the regular polygon and h is the apothem, that formula can be represented as 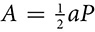 , where a is the length of the apothem and P is the perimeter of the regular polygon.
, where a is the length of the apothem and P is the perimeter of the regular polygon.
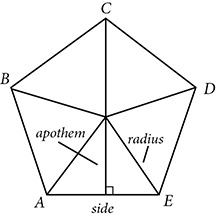
If you are not given the apothem directly, you may be able to find it from other information. Because the apothem divides the small isosceles triangle into two right triangles, if you know the side and the radius, you can find the apothem using the Pythagorean theorem.
If you don’t have enough information to do that, calculate the measures of the angles in the small isosceles triangle and see if you have a special right triangle and can find the length of the apothem from that. If all that fails, you’ll need to use trigonometry.
Trigonometry comes up later in this book, but if you have a calculator with a key that says tan, you can find the apothem by multiplying half the length of a side times tan(measure of base angle of the little isosceles triangle).
EXAMPLE
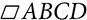 has AB = CD = 12 cm and the perpendicular distance between
has AB = CD = 12 cm and the perpendicular distance between 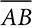 and
and  is 5 cm, the area of
is 5 cm, the area of 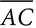 . M is the midpoint of
. M is the midpoint of 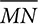 is parallel to
is parallel to  .
.
 .
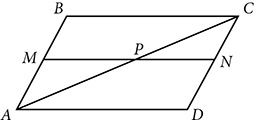
. . Prove ABCD is a parallelogram.
. Prove ABCD is a parallelogram.
 , ∠AFB ≅ CGD, and ∠BAE ≅ ∠DCE. Prove ABCD is a parallelogram.
, ∠AFB ≅ CGD, and ∠BAE ≅ ∠DCE. Prove ABCD is a parallelogram.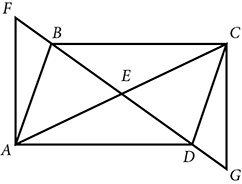

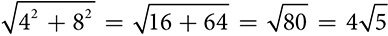 .
. square centimeters.
square centimeters.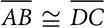 , and
, and  . Prove that FBCE is a rectangle.
. Prove that FBCE is a rectangle.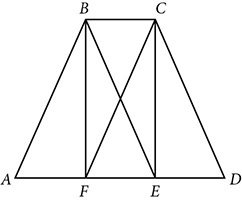
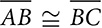 and ∠A ≅ ∠C. Prove HBDF is a rhombus.
and ∠A ≅ ∠C. Prove HBDF is a rhombus.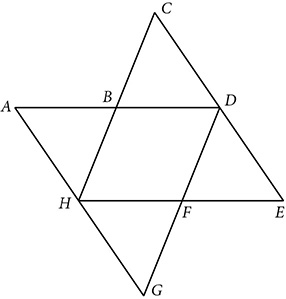
 and
and 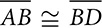 . F is the midpoint of
. F is the midpoint of 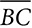 and E is the midpoint of
and E is the midpoint of  . Prove EBFD is a square.
. Prove EBFD is a square.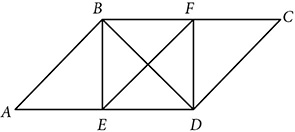
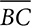 . If ∠A ≅ ∠D, explain how you can conclude that ΔBGC is isosceles but not equilateral.
. If ∠A ≅ ∠D, explain how you can conclude that ΔBGC is isosceles but not equilateral.
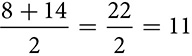 cm and the area of the trapezoid is 11 ⋅ 12 = 132 square centimeters.
cm and the area of the trapezoid is 11 ⋅ 12 = 132 square centimeters. connects M, the midpoint of
connects M, the midpoint of  , with N, the midpoint of
, with N, the midpoint of  . Prove that quadrilateral AMNC is a trapezoid. If the area of ΔABC is 64 cm2, what is the area of the trapezoid AMNC? Explain your reasoning.
. Prove that quadrilateral AMNC is a trapezoid. If the area of ΔABC is 64 cm2, what is the area of the trapezoid AMNC? Explain your reasoning.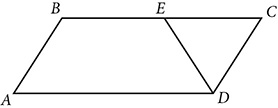
 and
and  . Diagonals
. Diagonals  are drawn. Prove
are drawn. Prove 
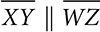 . m∠W = 2x + 17, m∠X = 5x + 2, and m∠Y = 4x + 3. Is WXYZ an isosceles trapezoid? Explain your reasoning.
. m∠W = 2x + 17, m∠X = 5x + 2, and m∠Y = 4x + 3. Is WXYZ an isosceles trapezoid? Explain your reasoning.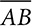 , to N, the midpoint of
, to N, the midpoint of  . If MBCN is rotated 180°clockwise about N, what type of quadrilateral is formed? Explain how you would find the area of this quadrilateral and show that it leads to the formula for the area of a trapezoid.
. If MBCN is rotated 180°clockwise about N, what type of quadrilateral is formed? Explain how you would find the area of this quadrilateral and show that it leads to the formula for the area of a trapezoid.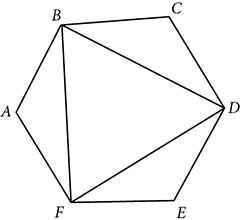


 .
.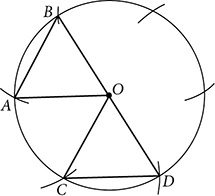
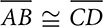 ?
?  ?
? 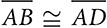 ? What type of parallelogram is inscribed?
? What type of parallelogram is inscribed?