Chapter 2: The Basic Data Types, Constants, and Variables Used in C++
In any programming language, being familiar with the generally used constants and variables is very important. In a programming language that is more object-oriented, such as C++, it becomes even more important to learn about at least the basics of the data types and objects that are commonly incorporated into C++ programs. As such, this chapter will focus on the elements mentioned above and aim to equip the reader with all the basics necessary for them to understand and create more complex and effective C++ programs in the future.
The Fundamental Data Types
In this section, we will discuss what a type refers to in a C++ program and understand the different fundamental data types available for use in the C++ programming language.
In programming, we have to take the different types of data into consideration, which can be used by the program to perform a task or solve a problem. Moreover, a computer does not work with only a single data processing method. To make use of the computer’s ability to process and save data through various methods, we need to know what type of data we are dealing with or figure out the data type which is being fed into our C++ program.
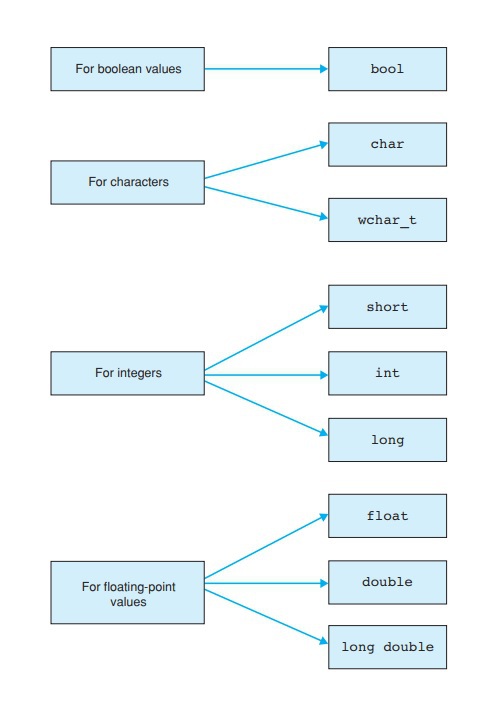
Generally, there are four major categories of data types in C++. These four data type categories are:
-
Boolean values
-
Characters
-
Integers
-
Floating-point values
Each data type requires a different approach to be adopted to make it possible for the computer to process the information they carry. That’s why it is very important to identify the data type in the program. The purpose of a data type is to elaborate:
For example, let’s consider an integer that we want to store as data. The number -1024 needs only 2 or 4 bytes of memory as storage space. In other words, if we want to store such an integer, we will need to allocate 2 or 4 bytes to do so. To access this data, we will need to access that part of memory where it has been stored and to do this, we simply need to read the corresponding byte numbers. Moreover, the program through which we are accessing this data type must also interpret the sequence of bytes, representing the data in memory, as an integer with a negative sign.
Here’s a chart representing the basic data types that are natively recognized by C++.
These are the fundamental data types that serve as the base for other data types such as vectors, pointers, and classes, etc. The C++ compiler has native support for these fundamental data types. As such, these data types are commonly referred to as built-in types
. We will now proceed to discuss each category of data type individually.
The ‘bool’ Data Type
A value obtained as a result of a logical comparison or association by using logic gates (such as AND or gates) is known as a Boolean
value and is referred to as a bool
data type. The distinguishing feature of this value is that it can be either of one of the logical states, i.e., true or false. The internal value of these logical representations is ‘numerical value 1’ for the ‘true state’ and ‘numerical value 0’ for the ‘false state.’
The Character Data Types
The character data type is used to save the code, which refers to a specific character. To be more specific, in programming, each character code is represented by an integer that is associated with the character. For instance, the integer associated with the character code of “A”
is ‘65’. Over the years, many character code sets have been developed to facilitate the digitization of writing. However, some sets have different character codes representing a particular character. So whenever a character is to be displayed on a screen connected to a computer, the associated character code is translated by the processor, and the resulting character is shown.
Although there are many character sets available in programming, the C++ language does not restrict the user to any particular set. However, character sets that contain the American Standard Code for Information Interchange, or more commonly referred to as ASCII code is preferred. This is a 7-bit character code set, and as such, it features 32 code characters and 96 printable characters.
In C++, the character data type features two major type containers, the char type,
and the wchar_t type
. The main difference between these two types is the storage they use to allocate the character codes. The char type
uses 8-bits (or one byte) of storage, making it suitable for extended character sets such as the ANSI character set. At the same time, the wchar_t type
uses 16-bits (or 2 bytes) of storage to allocate the character codes making it suitable for the modern Unicode characters. This is also the reason why the whchar_t
type is referred to as the ‘wide character set.’
The Integer Data Type
There are three integral types used to represent integer data. These types are different from each other based on the range of values they can represent. These integral data types are the following:
-
int
and unsigned int
-
short
and unsigned short
-
long
and unsigned long
The table shown below highlights the properties of and specification (storage space and the supported range value) of each integral data type.
|
Type
|
Size
|
Decimal Range of Values
|
|
Char
|
1 byte
|
-128 to +127 or 0 to 255
|
|
Unsigned char
|
1 byte
|
0 to 255
|
|
Signed char
|
1 byte
|
-128 to +127
|
|
Int
|
2-byte resp.
4 byte
|
-32768 to +32767 resp
-2147483648 to +2147483647
|
|
Unsigned int
|
2-byte resp.
4 byte
|
0 to 65535 resp.
0 to 4294967295
|
|
Short
|
2 byte
|
-32768 to +32767
|
|
Unsigned short
|
2 byte
|
0 to 65535
|
|
Long
|
4 byte
|
-2147483648 to +2147483647
|
|
Unsigned long
|
4 byte
|
0 to 4294967295
|
The int
type is like a self-fitting and self-adjusting integral type. It adapts to the register of the computer on which it is being used. For example, if the int
type is being used on a 16-bit system, then it will have the same specifications as the short
type. Similarly, if the int
type is being used on a 32-bit system, then it will have the same specifications as the long
type.
You might have also noticed a data type that isn’t a part of the integral data type family. This is the char
type belonging to the character data type. The reason as to why the char
type is included in this table is because C++ evaluates character codes just like any ordinary integer. Due to this, programmers can perform calculations on variables that are stored in char
and wchar_t
type in the same way as they would with variables stored in int
type. However, it is important to keep in mind that the storage capacity of a char
type is only a single byte. So, depending on how the C++ compiler interprets it (as either signed or unsigned), the range of values you can use with it are only from -128 to +127 and 0 to 255, respectively. On the other hand, the wchar_t
type is an extended integral type as opposed to the char
type being a simple integral
type and is commonly defined as unsigned short
.
Now let’s discuss the signed
and unsigned
modifiers in the integral type. A signed integral has the highest valued bit as the representative of the sign of the integer value. On the other hand, unsigned integrals do not feature the highest bit representing the sign, and as a consequence, the values that can be represented by unsigned integral are changed. However, the memory space required to store the values is the same for signed and unsigned integral types. Normally, the char
type is interpreted by the compiler as ‘signed,’ and as such, there are the modifiers result in three integral types, char, signed char
and unsigned char
.
Users can take advantage of a header file named as ‘climits
’ that defines the integral constants, for instance:
As their name suggests, these constants represent the smallest and largest values of their corresponding integral types. To understand integral types better, let’s implement this header file in a C++ program and use these constants to output the values of the int
and unsigned
int
types.
#include <iostream>
#include <climits>
// Definition of INT_MIN, ...
using namespace std;
int main()
{
cout << "Range of types int and unsigned int"
<< endl << endl;
cout << "Type
Minimum
Maximum"
<< endl
<< "--------------------------------------------"
<< endl;
cout << "int "<< INT_MIN << " "
<< INT_MAX << endl;
cout << "unsigned int " << " 0 "
<< UINT_MAX << endl;
return 0;
}
The Floating Point Data Type
Floating-point data refers to those numbers that have a fractional portion indicated by a decimal point. Unlike integers, floating-point values need to be stored according to a preset accuracy. This is in accordance with how decimal numbers are treated mathematically, i.e., the least significant numbers are ignored or rounded off. According to the preset accuracies, there are three floating-point types which have been listed below:
-
floa
t
:
corresponds to a simple accuracy preset
-
doubl
e
:
corresponds to a double accuracy preset
-
long doubl
e
:
corresponds to a high accuracy preset
An important thing to note regarding floating-point types is that the maximum and minimum value range along with the accuracy of a particular type is dependent on two factors:
-
The total memory allocated by the floating-point type.
-
The internal representation of the floating-point type.
Now let’s discuss and clarify the concept of ‘Accuracy’ in floating-point numbers. In numerical representation, the more numbers a value has after decimal points, the more accurate it is. In other words, high accuracy means that the floating-point value has a higher amount of numbers coming after the decimal point. Similarly, low accuracy means that the floating-point value has fewer numbers after the decimal point. For example, the floating-point number 22.123456 has a higher accuracy as compared to the floating-point number 22.123.
Now we must understand how is this concept of ‘Accuracy’ leveraged by programmers. , when we have a number that is accurate up to six decimal places, we can store the same value as a separate and distinguishable number as long as it differs from the original number up to at least one decimal place. However, the same convention does not hold necessarily always hold true if we try to store a number that is accurate up to 5 decimal places along with the same number that is accurate up to 4 decimal places as separate numbers in a floating-type of 6 decimal place accuracy. To clarify, there’s no guarantee that the two numbers 22.12345 and 22.1234 will have different decimal places when their accuracy is brought up to 6 decimal places.
In cases where it becomes crucial for your program to represent a floating-point number in an accuracy that is strictly supported by a particular device or system, it is recommended to first refer to the values that have been defined in the header file named ‘cfloat
.’
In conclusion, there are mathematical representations of data that are handled primarily handled by two data types. Depending on the arithmetic nature of the value (integer or a number with decimal points), it can be either stored in the integral type
or the floating-point type
. A recap of all the corresponding types has been listed below.
Integral Data Types
bool
char, signed char, unsigned char, wchar_t
short, unsigned short
int, unsigned int
long, unsigned long
Floating-Point Data Types
float
double
long double
The Institute of Electrical and Electronic Engineering, also referred to as IEEE, has provided the field of computer programming with a universal format that is used to represent the floating-point types
. The following table briefly discusses this format representation.
|
Type
|
Memory
|
Range of Values
|
Lowest Positive Value
|
Decimal Accuracy
|
|
Float
|
4 bytes
|
–3.4E+38
|
1.2E—38
|
6 digits
|
|
Double
|
8 bytes
|
–1.7E+308
|
2.3E—308
|
15 digits
|
|
long double
|
10 bytes
|
–1.1E+4932
|
3.4E—4932
|
19 digits
|
In the following sections, we will briefly discuss the operator ‘sizeof
’ and talk about the classification of data types according to the nature of the object they represent.
The ‘sizeof’ Operator
When we need to confirm the required memory to store a certain type of object, we simply use the ‘sizeof’ operator for this purpose. For instance, if we use this operator as shown below:
sizeof (name of the object)
the program will tell us the memory necessary for storing the object. In other words, the operator ‘sizeof’ provides the object’s memory requirements while the ‘name’ parameter defines the object itself, or it’s the corresponding type. For instance, by inputting the proper data into the above parameter, let’s say sizeof(int)
. If you remember that the int type is adjusted itself according to the system, then you will also understand as to why the sizeof operator gives different values depending on the system (it can be either 2 or 4). Similarly, if we use this operator for floating-point type, i.e., sizeof(float),
then we will be given a value of 4 representing the memory required to store the object.
Classification
Based on the nature of the object, we can classify two of the three fundamental data types (integer types and floating-point types
) as arithmetic data types as we can perform arithmetic calculations on the variables of these types using arithmetic operators.
Until now, we have discussed objects that represented values and classified them accordingly. However, there are also those objects that do not represent any value, for example, a function. To classify such expressions, we simply represent them through the void type
. In other words, the void type includes those expressions that do not represent any value. As such, a typical function call can be represented by a void type.
The Fundamental Constants
A constant is also referred to as a “literal
.” We deal with constants throughout programming, even if you don’t know about them. For instance, we just learned about the Boolean data type. A Boolean value can be either 1 or 0, i.e., True or False. The keyword here ‘True and False’ are both Boolean constants. Similarly, every number, character, and even a string (sequence of characters) is a ‘constant.’
Constants are directly related to data types. The very basic purpose of a constant is to represent values, which in turn represents the type. Hence, depending on how the constant is being used, we can define the type of the value accordingly.
Based on the above discussion, we can conclude that there are four fundamental constants in C++. These constants are:
-
Boolean constants
-
Numerical constants
-
Character constants
-
String constants
We will now discuss each fundamental constant separately.
-
Boolean Constants
A Boolean constant is a keyword used to represent either of the two possible values. True and False are both Boolean constants. Boolean constants belong to the bool
type and can be used to set up conditionals within a program or even set flags that functions to represent the two states.
-
Integral Constants
Standard decimal, octal, or even hexadecimal numbers are referred to as integral constants. Let’s briefly discuss these three numbers and how they can be distinguished from each other.
-
A decimal constant is a number belonging to the decimal number system (base 10). A decimal number never begins with a zero. 110, 124020 are both decimal numbers.
-
An octal constant is a number belonging to the octal number system (base 8). An octal number always begins with a zero as the leading digit. For instance, 088 and 022445 are both octal numbers and are referred to as octal constants.
-
A hexadecimal constant is a number belonging to the hexadecimal number system (base 16). A hexadecimal number always begins with a character pair. This character pair can be either “0x” or “0X”. For instance, 0x224A and 0X21b4F are both hexadecimal numbers. The Alphabetical numbers represent digits greater than nine up to 15 (for example, A represents 10, B represents 11 and F represents 15). There is no uppercase or lower-case capitalization restriction imposed on hexadecimal numbers.1
Usually, integral constants are assigned to the int
type. However, if the constant value turns out to be too large for the int
type to handle, then a type that is suitable to deal with that value will be used instead. Regardless, it is important to know the ranking of the integral types:
-
int
-
long
-
unsigned long
To designate either the long or unsigned long type to an integral constant, we simply attach the first alphabetical letter of the type to the number. For example, if we were to assign the number 15 to a long type, then we would do so by either adding ‘L’ or ‘l’ to the number. Similarly, if we were to assign the same number to the unsigned long type, then we would do so by using the ‘
UL’ or ‘ul’ letter. For assigning a number to the unsigned int type, we only need to use the letter ‘U’ or ‘u.’ This has been demonstrated below:
15L and 15l correspond to the type long
15U and 15u correspond to the type unsigned int
15UL and 15ul correspond to the type unsigned long
A detailed example of all the integral constants has been demonstrated in the table shown below.
|
Decimal
|
Octal
|
Hexadecimal
|
Type
|
|
16
|
020
|
0x10
|
int
|
|
255
|
0377
|
OXff
|
int
|
|
32767
|
077777
|
0x7FFF
|
int
|
|
32768U
|
0100000U
|
0x8000U
|
unsigned int
|
|
100000
|
0303240
|
0x186A0
|
int (32-bit)
long (16-bit)
|
|
10L
|
012L
|
0xAL
|
long
|
|
27UL
|
033UL
|
0x1bUL
|
unsigned long
|
|
2147483648
|
020000000000
|
0x80000000
|
unsigned long
|
From the table shown above, you can see how each value has been represented in different ways.
Here’s an example of a program that incorporates the integral constant concepts we have discussed so far.
// To display hexadecimal integer literals and
// decimal integer literals.
//
#include <iostream>
using namespace std;
int main()
{
// cout outputs integers as decimal integers:
cout << "Value of 0xFF = " << 0xFF << " decimal"
<< endl; // Output: 255 decimal
// The manipulator hex changes output to hexadecimal
// format (dec changes to decimal format):
cout << "Value of 27 = " << hex << 27 <<" hexadecimal"
<< endl; // Output: 1b hexadecimal
return 0;
}
Floating-Point Constants
A floating-point value has two elements, an integral element, and a fractional element. The fractional part of the number is separated from the integer by a decimal point. That’s why although floating-point values are usually represented as decimals, they can also be represented through exponential notation as well. For example, a typical floating-point number that is accurate up to one decimal place can be represented as shown below:
20.7
Similarly, if we have a number 1.5*10-2
then instead of inputting it in its decimal form, we can simply store it in its exponential form as well, which would be 1.8E-2
. The arithmetic type used to store these objects would be the double
type by default. However, the constant can be manually designated as a float
type as well by adding ‘F’ or ‘f’ to the value. Similarly, you can assign it to the long double
type as well by adding ‘L’ or ‘l.’
The following table shows a few examples of how floating-point constants can be represented in different ways.
|
7.19
|
16.
|
0.55
|
0.00001
|
|
0.719E1
|
16.0
|
.55
|
0.1e-4
|
|
0.0719e2
|
.16E+2
|
5.5e-1
|
.1E-4
|
|
719.0E-2
|
16e0
|
55E-2
|
1E-2
|
Character Constants
A character that has been enclosed in single quotes is identified as a character constant. Character constants are generally assigned to the char
type. Each character has a numerical code that represents the character itself. For instance, in the ASCII code, the character ‘A’ is numerically represented by the number ‘65’. The table shown below elaborates a few character constants along with their decimal value in the ASCII code.
|
Character Constant
|
Character
|
ASCII Code Decimal Value
|
|
‘A’
|
Capital Alphabet A
|
65
|
|
‘a’
|
Small Alphabet a
|
97
|
|
‘ ’
|
Blank space
|
32
|
|
‘.’
|
Dot
|
46
|
|
‘0’
|
Numerical Digit 0
|
48
|
|
‘\0’
|
Terminating Null Character
|
0
|
String Constants
We are already familiar with string constants as we had dealt with them in the first chapter when we were discussing the text output for the cout
stream in C++ programs. Regardless, you should remember that a sequence of characters (such as a sentence or a phrase) enclosed within double quotes is considered as a string constant. For example, “Press the Accept button to proceed!” is a string constant.
It is important to note that when a string sequence is stored internally, the double quotes are not included. Instead, a terminating null character (\0) is placed at the end of the string sequence to indicate that the sequence has ended. As such, apart from the bytes required to store the individual characters, a string sequence also uses another byte to store the terminating null character as well. That’s why string constants take up one additional byte than their usual memory requirements. The following figure depicts this internal representation of the string sequence “Hello!”
Escape Sequences
Another aspect to consider when talking about characters in programming is those that are non-graphic or not displayed on the screen but do have a purpose. For example, look at your keyboard and go through the buttons that, when pressed, display a character on a word processor. As soon as you think about it, you’ll notice that certain characters do not display any character on the screen when pressed, such as the ‘Tab’ button, the ‘Shift’ button, and so on. Such non-graphic characters are referred to as ‘escape sequences’ and its effect depends on the device on which it is being used. For example, the Tab escape sequence (\t) depends on the default setting of the width space that has been predefined, which is eight blanks.
In addition, note that every escape sequence has a back-slash at the start of the character. The table shown below elaborates on several escape sequences along with their decimal values and effects.
|
Character
|
Definition
|
ASCII Code Decimal Value
|
|
\a
|
alert (BEL)
|
7
|
|
\b
|
backspace (BS)
|
8
|
|
\t
|
horizontal tab (HT)
|
9
|
|
\n
|
line feed (LF)
|
10
|
|
\v
|
vertical tab (VT)
|
11
|
|
\f
|
form feed (FF)
|
12
|
|
\r
|
carriage return (CR)
|
13
|
|
\”
|
" (double quote)
|
34
|
|
\’
|
' (single quote)
|
39
|
|
\?
|
? (question mark)
|
63
|
|
\\
|
\ (backslash)
|
92
|
|
\0
|
string terminating character
|
0
|
|
\ooo (up to 3 octal digits)
|
the numerical value of a character
|
ooo (octal)
|
|
\xhh (hexadecimal digits)
|
the numerical value of a character
|
hh (hexadecimal)
|
Octal and hexadecimal escape sequences allow users to represent character codes differently. For example, if you want to express the alphabet ‘A,’ then you can convert its decimal value to an octal value and then use the octal escape sequence to express it. In ASCII code, you will need to use the decimal value 65; however, if you’re not using the ASCII character code set, then you can simply use ‘\101’ to express the same alphabet. Similarly, you will have to use ‘\x41’ if you want in the hexadecimal escape sequence to express the alphabet ‘A.’ Although escape sequences can be used in this way, they are primarily used to express those characters that are non-printable. For example, if you want to represent the character ‘ESC,’ which serves as a control sequence for printers, then you can express it by using an escape sequence (for octal \33 and for hexadecimal \x1b).
The Fundamental Variables
Variables are commonly referred to as ‘objects,’ especially if they are part of a class. Variables are very important in programming as they serve as containers for data (numbers, characters, and even entire sequences). Moreover, by using variables, the program can easily process the data. In this section, we will discuss all the fundamental concepts about variables.
Defining Variables
A variable is an empty container that is abstract to the program until it has been defined. By defining a variable, we mean that we are storing data inside this abstract container by allocating memory to it, making it meaningful for the program. So, in a sense, we specify the data type and reserve the memory, which is to be used by the variable once it has been initialized. Once a variable is defined, think of it as a redirection tool. When a user refers to this variable, the program automatically fetches the corresponding data associated with the variable in the memory space in which it is allocated, so that the program can process it. In this way, we can perform operations on this data linked to the variable easily. A standard definition of a variable has a proper syntax that needs to be followed. This syntax is:
By looking at this syntax, we can see that the argument ‘typ’
is actually mentioning the variable’s type. ‘name1’ is simply the variable’s name that the programmer specifies. Once defined, whenever we want to specify the variable in any part of the program, we use this particular name. In this syntax, we can also see a square bracket that houses another variable by the name of ‘name2’. The square brackets tell the program that the variables mentioned inside it are not entirely necessary, and the program can ignore this portion if it needs to. This means that we can define and store multiple variables in one go. The following program demonstrates how we can define variables practically:
char c;
int i, counter;
double x, y, size;
Another important thing to note is that variables can be defined in two ways. They can be defined within the function of the program or outside the program’s function. For example, at any portion of the program as long as it isn’t done within the function. However, defining a variable either within or outside a function has certain effects, respectively. These have been listed below:
-
A variable defined outside a function has a global property within the program. This means that all of the program’s functions can use this variable.
-
A variable defined inside a function has a local property within the program. This means that the variable can only be used by the function in which it has been originally defined and not by any other function of the program.
A local variable can be defined at any point in the function where a statement is permissible.
Initialization
The initialization of a variable essentially refers to the assigning of value to the variable mentioned above. When a variable is being defined, it is also initialized at the same time. Once the variable is defined, we simply assign a value to it immediately after the definition syntax to initialize it.
A variable can be initialized by using either of the two methods
char k = ‘a’;
char k(a);
Similarly float x(1.112);
A global variable that is not initialized has a default value of ‘0’. However, this does not apply to local variables as a local variable that hasn’t been initialized will be assigned an undefined value by default.
Here’s an example of a program incorporating the concepts we have discussed so far.
// Definition and use of variables
#include <iostream>
using namespace std;
int gVar1;
// Global variables,
int gVar2 = 2;
// explicit initialization
int main()
{
char ch('A');
// Local variable being initialized
// or: char ch = 'A';
cout << "Value of gVar1:
" << gVar1 << endl;
cout << "Value of gVar2:
" << gVar2 << endl;
cout << "Character in ch:
" << ch << endl;
int sum, number = 3; // Local variables with
// and without initialization
sum = number + 5;
cout << "Value of sum:
" << sum << endl;
return 0;
}
Upon executing this program, the computer will display a result as shown below:
Value of gVar1: 0
Value of gVar2: 2
Character in ch: A
Value of sum: 8
Constant and Volatile Objects
In this section, we will discuss two important keywords in programming that can heavily affect the properties of an object. These keywords are:
Constant Objects
Let’s say we already have an object of a specific type available for use. We can change the properties of the object by using the const
keyword in place of its type. Doing so will create an entirely new object that is specifically ‘read-only.’ As we know from our daily interaction with computers, a read-only file can only be accessed and cannot be modified by the user. The same is the case for a constant object. Since its properties have become read-only (in other words, the object itself has become constant), it renders the program helpless when it attempts to modify the object. So a constant object, once defined and initialized, cannot be modified later on. Due to this nature, the programmer must initialize the constant object at the same time it is defined; otherwise, it will be a read-only object that is assigned a default value.
An example of a constant object being defined and initialized is shown below:
const double pi = 3.1415947;
By creating such an object, the program will not be able to modify the value of this object in any scenario. Even if we introduce a statement like this into the program:
pi = pi + 2.0; // invalid
The program will only return an error message as a result.
Volatile Objects
A volatile object is the polar opposite of a constant object. However, volatile objects are rarely used in programs. An object created by using the keyword volatile
will have properties that allow not only the program in which it resides but also other programs and external events as well to modify the object. External events are usually triggered through interrupts or hardware clocks, for instance:
volatile unsigned long clock_ticks;
In this way, even if the program does not directly modify the values of this variable, the hardware clock definitely will. As such, the program has to assume the value of this variable has changed since the last time it was accessed. For this purpose, the compiler constructs a machine code that allows it to scan and access the variable’s current value instead of outputting the value on which it was initialized.
Another interesting point is that we can use both const
and volatile
keywords at the same time on the same variable. For example, if we were to use these keywords, then the resulting variable’s properties cannot be modified by the program itself. Still, it can be modified by external events such as the hardware clock. An implementation of this concept has been shown below:
volatile const unsigned time_to_live;