The Logic of Classification
THE ATHENIAN Assembly often disappointed the classical Greeks, but geometry deeply impressed them. Euclid’s Elements was composed about a generation after Aristotle, but geometry handbooks were already in circulation by the time Aristotle taught. What most impressed the Greeks about geometry was its certainty and finality. Unlike the vagaries of politics, which often tempt us with a bad argument or force us to rely ultimately on an intelligent guess, the geometry of the ancients seemed to offer conclusive proof. Once the definitions, postulates, and axioms were laid out, the theorems appeared to follow as a matter of logical necessity. It is easy to imagine how intelligent observers in Aristotle’s day would have longed to achieve a similar certainty in all fields of human endeavor and how some of them would have sought out the secret of necessity in geometry’s serene and timeless diagrams.
This reverence for geometry appears repeatedly in the dialogues of Plato,1 but a similar sense of certainty and timeless serenity is also present in Aristotle’s logic. Aristotle’s examples of logical argument often come from geometry, but, more important, his logical system has the effect of proving claims about whole classes of objects—just as Euclid’s theorems make claims about all circles, all triangles, or all bisected angles. The logical secret Aristotle sought from geometry was the secret behind classification.
To understand Aristotle’s approach better, let’s turn first to an example from a very different time—a fanciful example, divorced from the blood and turmoil of Athenian politics and coming instead from the author of Alice in Wonderland. Today we know the author of the Alice stories as Lewis Carroll, but he was actually Charles Dodgson, lecturer in mathematics and logic at Oxford University from 1855 to 1881. Carroll concocted the following argument as an exercise for his students:
I trust every animal that belongs to me.
Dogs gnaw bones.
I admit no animals into my study unless they will beg when told to do so.
All the animals in the yard are mine.
I admit every animal that I trust into my study.
The only animals that are really willing to beg when told to do so are dogs.
Therefore, all the animals in the yard gnaw bones.2
Despite its circuitousness, the argument can be represented like this:
All As are Bs.
All Cs are Ds.
All Es are Fs.
All Gs are As.
All Bs are Es.
All Fs are Cs.
Therefore, all Gs are Ds.
This equivalence in structure is, of course, not immediately apparent, but it becomes easier to see with a series of substitutions.
As = animals that belong to me
Bs = animals I trust
Cs = dogs
Es = animals admitted to my study
Fs = animals that will beg when told to do so
Gs = animals in the yard
Thus the argument can be rewritten:
All animals that belong to me are animals I trust.
All dogs are animals that gnaw bones.
All animals admitted to my study are animals that will beg when told to do so.
All animals in the yard are animals that belong to me.
All animals I trust are animals admitted to my study.
All animals that will beg when told to do so are dogs.
Therefore, all animals in the yard are animals that gnaw bones.
(As it turns out, the argument is valid.)
These manipulations all rest on techniques pioneered by Aristotle, who investigated arguments of this type by distinguishing what he regarded as the four most basic “predications,” or what we might now call the four most basic classifications.3 He focused on only those cases where one class or category could be said to do the following:
wholly include the other,
wholly exclude the other,
at least partly include the other, or
at least partly exclude the other.
These are the four “categorical propositions”4 of Aristotelian logic, and traditionally they are expressed as follows:
All As are Bs.
No As are Bs.
Some As are Bs.
Some As are not Bs.
(The word “some” here is construed to mean “at least one, perhaps all.”) These four types of proposition can then be combined to generate logically valid forms involving more than two classes, like this:
All As are Bs.
No Cs are Bs.
Therefore, no As are Cs.
(For example, “All Spartans are dangerous, and no Thebans are dangerous; therefore no Spartans are Thebans.”)
Now quite apart from whether this kind of analysis would actually have saved the ancient Athenians from the disasters of their time, Aristotle became interested in the subject for its own sake. One effect of those disasters had been to draw attention to the difference between valid arguments and specious ones. Aristotle wanted to investigate valid reasoning as such and to find ways of distinguishing the valid from the invalid—something the Assembly had often failed to do. And his analysis had a further, crucial consequence: long arguments with many premises (arguments like Lewis Carroll’s) could be reduced to a series of short ones, all having just two premises and a conclusion.
For example, Lewis Carroll’s argument can be reduced to a series of short ones where all the premises in the series come from the original argument or can be deduced from the original premises. Thus each new argument in the following series builds on the preceding one:
All animals in the yard are animals that belong to me.
All animals that belong to me are animals I trust.
Therefore, all animals in the yard are animals I trust.
All animals in the yard are animals I trust (deduced previously).
All animals I trust are animals admitted to my study.
Therefore, all animals in the yard are animals admitted to my study.
All animals in the yard are animals admitted to my study (deduced previously).
All animals admitted to my study are animals that will beg when told to do so.
Therefore, all animals in the yard are animals that will beg when told to do so.
All animals in the yard are animals that will beg when told to do so (deduced previously).
All animals that will beg when told do to so are dogs.
Therefore, all animals in the yard are dogs.
All animals in the yard are dogs (deduced previously).
All dogs are animals that gnaw bones.
Therefore, all animals in the yard are animals that gnaw bones.
This series never makes use of any premises that were not already contained in the original argument or derivable from the original premises. And what the series then does is connect the class of animals in the yard to each new class in turn until reaching the final conclusion that all animals in the yard are animals that gnaw bones.
As a result, Aristotle’s strategy was to determine which of these short forms of argument were valid or invalid and then use this information to evaluate any longer forms. The upshot, he hoped, would be to capture the logic behind all forms of human knowledge.5 The short forms, which all have only two premises and a conclusion and three key terms (e.g., A, B, and C) are now called “categorical syllogisms.”6 Yet this was only part of Aristotle’s insight, which, to repeat, is an insight into the logic of classifying.
As a biographical matter, Aristotle’s interest in classifying may have derived from his father (whose methods as a doctor would have stressed the classification of disorders), but he may also have come to it from the direct observation that people commonly classify (or predicate) more than they realize. Historically, as the classical Greeks were turning over more of their political decision-making to vast public assemblies, they were also developing their keen taste for geometrical theorems, which made claims about whole classes of figures. The new power of the assemblies emphasized the importance of argument, but for many Greeks, the results of geometry came to loom ever larger as a tantalizing model of what rational argument might be. Aristotle’s logic, then, represents the culmination of these tendencies.7 Beyond these points, however, Aristotle’s analysis showed something more: the four categorical propositions are also related to one another in definable ways, ways we implicitly invoke every day. And in showing this, he raised deep questions about the peculiar nature of logical necessity.
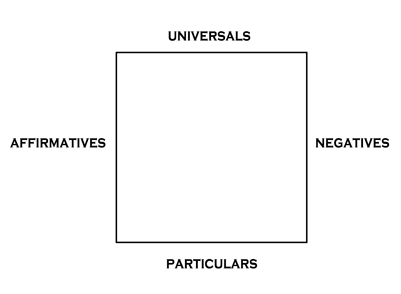
THE SQUARE OF OPPOSITION
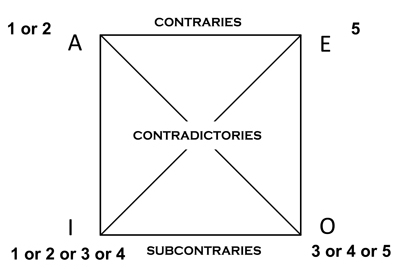
The best way to grasp Aristotle’s further insight into these matters is to look at a picture developed in Roman times that incorporates his observations. The picture is called the square of opposition and is given in figure 3.1. Consider what the picture does. Based on various remarks in Aristotle’s treatises,8 it tells us what conclusions can be drawn from any of the four categorical propositions about any of the others.
For example, the two propositions at the top of the square are “contraries,” meaning they can’t both be true together but might both be false.
Thus, if the sentence “All As are Bs” is true, then the sentence “No As are Bs” must be false; but if “All As are Bs” is false, then “No As are Bs” could be true or false. The two sentences can’t be simultaneously true but could be simultaneously false. (See figure 3.2.)
The two sentences at the bottom of the square (also represented in figure 3.3) have a different relationship. If “Some As are Bs” is true, then “Some As are not Bs” could also be true; but if one of the sentences is false, could the other also be false? If by “some” we mean “at least one and maybe all,” then the two sentences can’t both be false.9 Instead, at least one must be true. (That is, if it is false that “at least one A is a B,” then it is necessarily true that “at least one A is not a B.”) As a result, the two sentences aren’t contraries but “subcontraries”—they can’t both be false.
Now look at the first and last of the categorical propositions in the square as shown in figure 3.4. In this new comparison, one of the sentences is true and the other false; if “All As are Bs” is true, then “Some As are not Bs” must be false, and vice versa. But notice that this is unlike the other relations we just looked at: the two sentences are now neither contraries nor subcontraries; their logical relationship is tighter because the truth or falsity of one fully determines the truth or falsity of the other. In the language of logic, they are “contradictories.” A little reflection will show that the remaining two sentences (“No As are Bs” and “Some As are Bs”) are also contradictories. (See figure 3.5.)

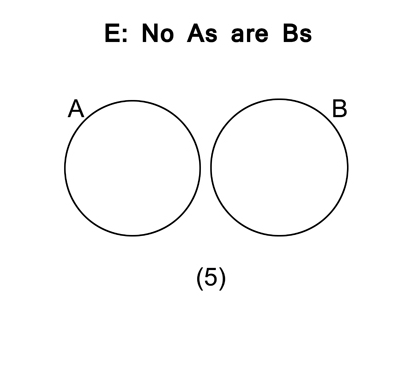
FIGURE 3.1. The Square of Opposition
(Definitions: “Contraries” can’t both be true. “Subcontraries” can’t both be false. “Contradictories” are pairs of sentences in which exactly one must be true and the other false.)
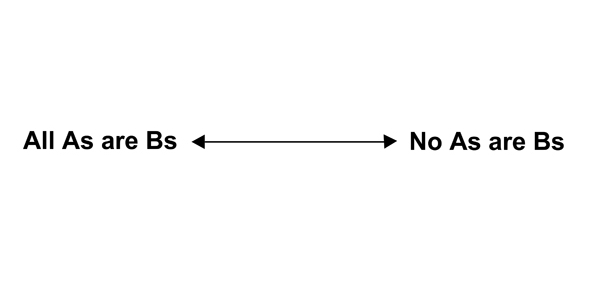
FIGURE 3.2. Contraries
(They can’t both be true but might both be false.)
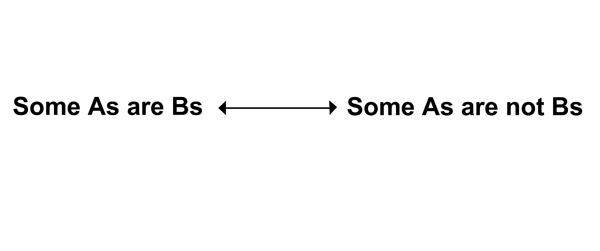
FIGURE 3.3. Subcontraries
(They can’t both be false but might both be true.)
There are a few other structural features to see in the square. First, the two sentences at the top of the square cover whole classes (“all” or “no”), for which reason they are called “universals”; the two sentences at the bottom make only partial claims about classes (“some”) and are called “particulars.” Also, the two on the left assert some sort of class inclusion, by way of affirmation, and are “affirmatives.” The two on the right assert class exclusion, by way of denial, and are “negatives.” In effect, then, there is an underlying configuration, like what is seen in figure 3.6.
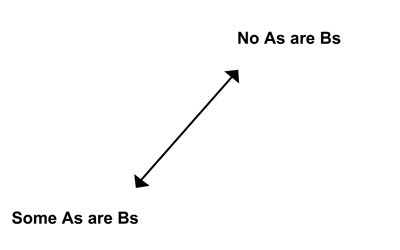
FIGURE 3.5. Contradictories
(Exactly one is true and the other false.)
Medieval logicians preferred to talk about all these points by using a shorthand consisting of vowels, and so (according to tradition) they are thought to have taken the two Latin words for affirmation and denial, affirmo and nego, and extracted some of the vowels and called the universal affirmative the “A,” the particular affirmative the “I,” the universal negative the “E,” and the particular negative the “O.”
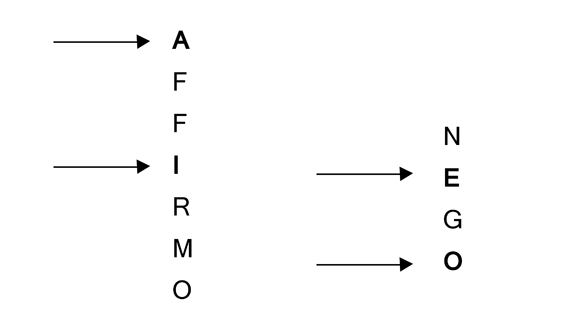
FIGURE 3.7.
(This is the origin of several mnemonic codes worked out in the Middle Ages for remembering which short forms—which categorical syllogisms—are valid or invalid.)10 And the square conveys one more point: if either of the universals is true, then the particular directly below it—its “subaltern”—must also be true. It follows, however, that if the particular is false, then the universal directly above must also be false.11 But here is the deeper question, the philosophical question, the one really worth asking: why does the whole thing work?
THE UNDERLYING MYSTERY OF THE SQUARE
The most tempting answer, probably, is that the square of opposition works because the relations it describes are just features of the way we use words, an aspect of our “language-game,” to use a phrase of the Austrian philosopher Ludwig Wittgenstein.12 The square works (it would seem) only because of the way we happen to use our logical vocabulary; if we used our logical words differently (we might suppose), then different things would be logical. But does this answer actually make sense?
Consider: the import of the square has been expressed in many languages, and the square was invented long before our language, English, ever existed. That aside, however, how do languages give rise to logical necessities in the first place? Instead, doesn’t a sense of logical necessity give rise to language? After all, languages work only because they follow rules, but no one follows a rule unless that person already senses what the rule logically implies. Logic makes language possible—not the other way around. Thus, to invoke a “language-game” theory to explain the existence of logical necessities (by saying that logical implications exist only because they follow logically from a language or from the structure of a language) is to argue in a circle. It puts the cart before the horse. (In fact, many philosophers have offered circular explanations of this sort, though without always realizing they were mixing up what depends on what.)13
But are there other ways to explain why the square works? Might one say, for example, that the ins and outs of the square are simply the implications of classification—the implications of inclusion or exclusion, partial or complete? The trouble with this further view is that an “implication,” by definition, is still a logical implication, and so the explanation is still circular. (We still haven’t explained why the implications have their peculiar design.) Why do logical necessities work out the way they do?
Alternatively, might we say that Aristotle’s insights—and perhaps all other logical truths—are really just “true by definition”? In other words, couldn’t we say that any logical relations we want to talk about happen to be the way they are only because they follow from some collection of definitions, definitions invented by logicians? Here, again, the explanation is circular. To say that one thing “follows” from another only because it follows from a definition still leaves unexplained why anything should follow to begin with. What we are really asking, in other words, is, “Why do logical necessities have their peculiar structure?” But let’s trying looking at this same question in another way—one that will perhaps throw more light on the matter.
We live in a world that requires many arbitrary choices, and many of our difficulties are problems of our own making. We make our bed, and we sleep in it. But our choices lead to difficulties in the first place only because they have consequences, and the relation between a choice and a consequence is never “made.” Instead, it can only be discovered. This is because a consequence is a matter of necessity, and necessities are at least partly determined by logic. (Indeed, without logic, there would be no whimsy—our sense of whimsy comes from contrasting the whimsical with the logical—but there would also be no tragedy; tragedy is what happens when we discover the inexorable consequences of some ill-considered choice.) Of course, in contemplating these matters, whether gay or grim, we can often supply arguments and, sometimes, compelling proofs for the existence of these consequences, consequences that often turn out to be surprising. But as for why they should exist in the first place and why they contain their secret surprises—these questions seem beyond us.
Here is yet one more observation on the peculiar question of why Aristotle’s system happens to work, this time from the eighteenth-century Swiss mathematician Leonhard Euler. Euler is a distinguished name in the history of mathematics, and it takes no great leap to see that many of these remarks about the strange quality of logical truths may well apply with equal force to mathematical truths. (Mathematical relations are logically connected and describable in detail, and yet they seem, in a deep sense, to be inexplicable.)14 Euler thought much about Aristotelian logic, and he offered a series of diagrams to express the import of the four basic sentences of the system. (Euler’s was not the first such analysis, but it is the most famous, and it was improved in the nineteenth century by the French mathematician J. D. Gergonne, who expressed it in five diagrams.15 This series of five gives us yet another way of looking at the square by allowing us to view it through the lens of geometry.)
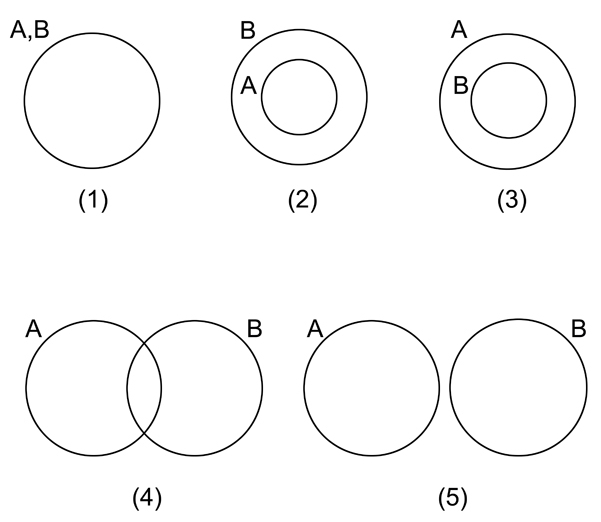
Euler’s approach (improved by Gergonne) works as follows. Given any two classes, As and Bs, we can picture their Aristotelian relationship as being like two circles, related in one of five ways (see figure 3.9).
In figure 3.9, the points in circles A and B represent the members of the classes A and B.
Now, if we look back at the original four categorical propositions, we can see that what the “A” proposition actually tells us is that either diagram (1) or diagram (2) represents the Aristotelian relationship, though we aren’t told which.
In both (1) and (2) in figure 3.10, it is true that all As are Bs.
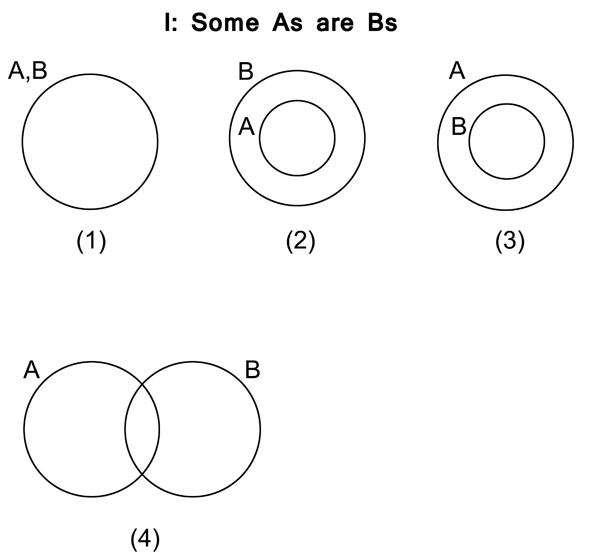
If we then look at the “I” proposition (figure 3.11), it says that (1), (2), (3), or (4) represents the relationship, though again we aren’t told which. (Remember that “some” means “at least one and perhaps all.”) In each diagram of figure 3.11, some As are Bs.
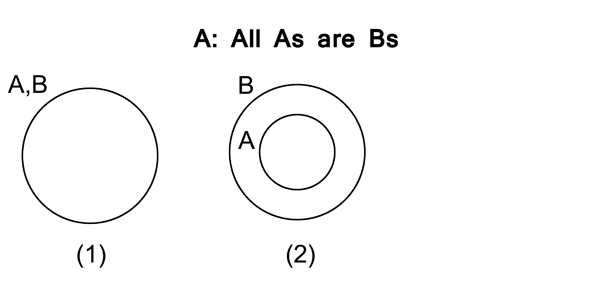
FIGURE 3.10.
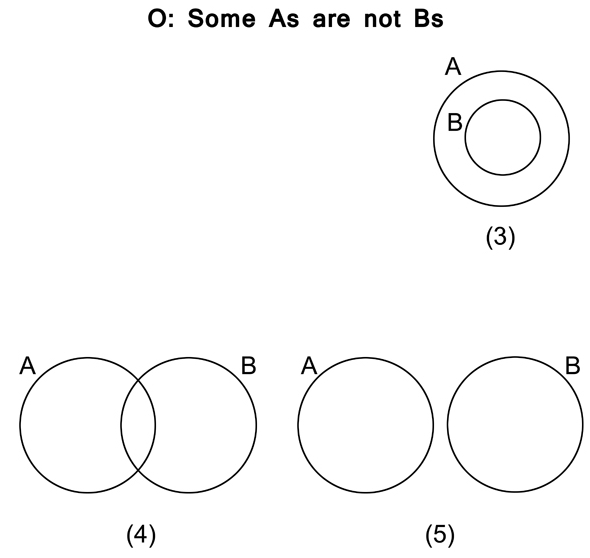
FIGURE 3.12.
Now look at the “O” (figure 3.12); what the “O” proposition says is that (3), (4), or (5) represents the relationship (and again, we don’t know which). In each diagram of figure 3.12, some As (at least some) are not Bs.
Finally, the “E” proposition (figure 3.13) says that only (5) represents the relationship. In none of the other diagrams is it true that no As are Bs.
There is only one more step to the analysis: notice that if any one diagram accurately represents the relationship, none of the others do. That is, all the diagrams are mutually exclusive. We can picture the four basic propositions of Aristotle in just this way, but if we now go back to the square of opposition from late antiquity, what we see is that all the connections it asserts follow necessarily from the equivalences pointed out by Euler (with help from Gergonne).
In figure 3.14, if 1 or 2 represents the relationship (the “A” proposition), then 5 (the “E” proposition) can’t. The two sets of diagrams are logical contraries. The diagrams for the “A” and “O” propositions are logical contradictories; if 1 or 2 represents the relationship, then 3, 4, and 5 can’t, and vice versa. As for the “I” and “O” propositions, they turn out to be subcontraries; at least one of the diagrams must represent the relationship, and so the two propositions can’t both be false but could still both be true. The “I” and “E” propositions turn out to be logical contradictories; the diagram that correctly captures the relationship must appear in exactly one of the two sets. In short, we can prove it all with diagrams.16
The most natural response, perhaps, is to say that Euler has at last explained the square of opposition because he has finally succeeded in defining the real meaning of the four original linguistic expressions; he has finally explained why it all hangs together. This, however, is a mistake. In fact, he has explained nothing of the sort, except in the sense that he has found yet another way to express the same underlying logical truths. After all, when we reason about classes, we are not merely reasoning about the circles in Euler’s diagrams. On the contrary, we are reasoning about shoes, ships, cabbages and kings, armchairs, galaxies, protons, integers, soldiers at war, theater tickets—whole hosts of things that look nothing like circles. The circles are merely representations once more, representations for describing an abstract structure.
The circles relate points on a plane to the members of classes, but this is only another way of discovering the logical relations that govern all classes, whether they are classes of points or classes of anything else. The circles help us discover these relations, but to discover isn’t to explain why they exist in the first place. Instead, we have only made their existence more conspicuous. It is as if Euler had given us yet another way to grasp logical necessities so that, in addition to hearing about them and thinking about them, we could also “see” them. But the most baffling thing of all is that, literally, we have no physical sensations of them whatever. We never see these abstract relations with the eye; we only grasp them with the mind.
WITTGENSTEIN’S PROPOSED SOLUTION
The impulse to explain all this as only an artifact of language (such that logic rests on language rather than the other way around) is very old.17 But the problem with this approach is that it begs the question. No language is intelligible in the first place unless it already conforms to something like logical rules. As a result, then, to argue that we grasp such rules only because we already know a language is to stand the correct mechanism on its head. Still, the impulse is very old, as we say, and its long history is worth a moment to consider.
During the last hundred years, the most prominent exponent of the linguistic view has been Wittgenstein, who was raised in Austria but taught logic and philosophy in England at Cambridge University in the 1930s and 1940s. He advanced this view in particularly stark form. Wittgenstein not only asserted that logical necessities depend on language rather than the other way around;18 he went further: he held that virtually all philosophical conundrums, whether about logic or anything else, are “meaningless” to the extent that if only you could speak a language correctly, such problems would effectively go away. For example, is there a god? Once you straighten out your language, what you discover (according to Wittgenstein) is that the question is “meaningless.” What makes an action right rather than wrong? Again, the question is “meaningless.” Is there an immortal soul? “Meaningless.” On Wittgenstein’s view, then, proper philosophy is mainly a matter of straightening out your language.
Of course, as soon as he said these things, he was constrained to explain just what he meant by the term “meaningless,” but when he then embarked on this further problem, he was immediately embroiled in puzzling out the various rules that supposedly define meaning. And the whole problem of rules drove him back once more into the dark thickets of logic.19
Wittgenstein arrived at his outlook in a peculiar way. Trained as an engineer and heir to an industrial fortune in Vienna, he became interested in symbolic logic as developed by the German logician and mathematician Gottlob Frege, and at Frege’s suggestion, he studied the techniques of this new logic with Bertrand Russell at Cambridge in 1912 and 1913. Not long afterward, however, as the Great Powers squared off at the approach of the First World War, Wittgenstein believed himself duty-bound to volunteer for the Austrian army, and soon he was posted to the Italian front as an artillery officer. During the war—amid its chaos and irrationality—Wittgenstein carried notebooks in his rucksack, and in his free time he composed his brooding masterpiece, his Tractatus Logico-Philosophicus. (He seems to have finished the manuscript in 1918; he already had drafts for the book when he was taken prisoner by the Italian Army a year earlier, and the economist John Maynard Keynes then managed to get the manuscript sent by diplomatic courier from Wittgenstein’s prison camp in Italy to Russell in England with the aim of having it published.)
Part of Wittgenstein’s appeal to his contemporaries was that he seemed to be offering solutions to the problems of his time; his emphasis on clarity and logical rigor seemed exactly the cure for the fanaticism and absurdity of the Great War, and this sentiment gained further strength with the rise of Hitler and the coming of World War II. Partly through Wittgenstein’s influence, logic became the core of so-called analytic philosophy through much of the twentieth century, and this emphasis on logic in academic philosophy was further strengthened by German émigrés fleeing Nazi persecution, who had found refuge in English and American universities and who understood from personal experience the importance of rationality and the social consequences of illogic.
Though some of Wittgenstein’s views later changed, he continued to work at his linguistic approach—from several different angles—for the rest of his life. Nevertheless, his basic claim about meaninglessness was mistaken, or so we believe. And at the risk of sounding recklessly brash, we think it was mistaken for a reason that is easy to see.
WITTGENSTEIN’S MISTAKE
Wittgenstein’s claim depended on confusing two very different sorts of meaninglessness: ambiguity and unintelligibility. But once the two sorts are distinguished, one can see fairly readily that his basic conjecture—most philosophical questions are “meaningless”—can’t be right. (The conjecture is actually much older than Wittgenstein; a version of it appears in the work of Thomas Hobbes and David Hume, and it is, thus, one of the stock theses of radical empiricism.)20
Here’s why the conjecture can’t be right: when we call a thing “meaningless,” we sometimes mean it has no fixed meaning, which is to say that it might mean any of two or more different things. Take, for example, the following controversy: if a tree falls in a forest where no one can hear it, does it make a sound?
Now, if by “sound” we mean the experience of hearing, then, by hypothesis, where no one can hear, there is no sound. But if by “sound” we mean something different—waves of pressure carried by the air—then a falling tree certainly does make a sound (unless it somehow flourishes in a vacuum). This dual use of the word “sound” is ambiguity, and it gives rise to all sorts of verbal disputes. This is what we sometimes mean when we call an expression “meaningless”; we mean that, in context, it has no single meaning—or, rather, too many meanings. We encounter this difficulty, for instance, when someone praises an artwork on the ground that the work is “distinctive”; the utterance could mean so many different things that it is hopelessly ambiguous.
Wittgenstein’s claim, however, was different. Wittgenstein meant that philosophical doctrines were unintelligible, in the same way that “Colorless green ideas sleep furiously” is unintelligible, or the way “’Twas brillig, and the slithy toves did gyre and gimble in the wabe” is unintelligible. (The first of these stock examples comes from Noam Chomsky, the second from Lewis Carroll.) Wittgenstein argued that the real problem is a tendency to use words that, in context, have no meaning whatever and without the speaker’s realizing it. We think we are saying something, but in fact we are saying nothing—not even something ambiguous.21 Of course, we often say things that are unintelligible to other people, but Wittgenstein meant that these same things are unintelligible even to ourselves. And viewed harshly, this conjecture is highly improbable. Why? Because it attributes to human beings something we just can’t do—or, rather, something we can’t do except in rare cases of psychosis or perhaps in strange dreams where no one else understands you, and you then wake up to find that the words you were saying in the dream aren’t intelligible in the first place.
Consider: human beings can certainly speak unintelligibly, and they can also fool other people into thinking they are being intelligible when they are not. (Professional comics perform this last little trick when they speak doubletalk.) But the one thing human beings can’t do, if sane, is fool themselves into this—into thinking they are being intelligible when they are not. Try it. Craft a sentence like, “It is time at last for the Empire State Building to blow its big nose,” and then persuade yourself that you are speaking intelligibly. You can no more do that than you can tickle yourself. You can tickle other people, but you can’t tickle yourself. Similarly, you can speak gibberish to others and sometimes fool them, but you can never use gibberish to fool yourself (at least if you are sane and awake).
Of course, Wittgenstein asserted that this is precisely what happens when people discuss philosophy: they fool themselves into thinking they are being intelligible when they are not. (The great attraction of his doctrine is that, if true, it would make the hard work of philosophical interpretation unnecessary; if the language is ambiguous, then it might still express a sound philosophical argument, and the only way to know that it doesn’t is to experiment with various interpretations. But if the language is unintelligible from the start, this labor can be avoided.)
Yet if Wittgenstein were right in his conjecture, then the same mistake would be empirically observable outside philosophy, as a matter of daily life. We would find people who are otherwise sane sincerely asking themselves whether the sky had brushed its teeth today, or whether the telephone had finished baking another dozen biscuits, or whether the twenty-first century would finally give its sister, the twentieth century, a big hug. The odd linguistic error Wittgenstein had in mind would be empirically observable everywhere. But it isn’t.
Instead, what we see in normal life is that the unintelligible is obviously unintelligible, and for a simple reason: the whole essence of the phenomenon is that our minds go blank. We just say, “It’s Greek to me.” By contrast, ambiguity doesn’t make our minds go blank; rather, it makes our minds drift from one idea to the next. These two phenomena seem similar, but they are different. And this is why Wittgenstein’s conjecture looks plausible—because we confuse the two situations. We often do speak ambiguously, and our minds often do wander from one idea to the next, and so we do indeed fall into countless ordinary mistakes, often without realizing it. But because the word “meaningless” can mean either “ambiguous” or “unintelligible,” we get mixed up and suppose that these mistakes must come not from ambiguous utterances, but from unintelligible ones.
(We should add that this difference between the ambiguous and the unintelligible has nothing to do with whether or not one construes the meaning of an utterance to be a mental occurrence; some philosophers have held meanings to be mental phenomena, whereas Wittgenstein, at least in his later work, insisted that the meaning of an expression was its use. Either way, however, ambiguous utterances have the effect of causing people to entertain multiple ideas, whereas unintelligible utterances have a different effect: they cause people to conjure up no ideas at all, except ideas about the sounds of the words themselves or the sheer strangeness of their combination. The first situation is treated by logic as a fallacy of ambiguity, but the second is an encounter with gibberish. And the point we stress is that these two experiences are empirically different, whatever theory of meaning one might prefer. In ordinary speech, we also apply the words “meaningless,” “gibberish,” and “nonsense” to implicit contradictions, and we sometimes use “meaningless” to describe trivial observations that have been expressed in pretentious, elevated diction. But none of these things are the same as the unintelligible.)22
To be sure, Wittgenstein was a shrewd philosopher of language, and, accordingly, we don’t mean to suggest for a moment that he would have had the slightest trouble in distinguishing ambiguity from unintelligibility in ordinary contexts. Nevertheless, the distinction is far easier to overlook in philosophical discussions where a speaker is unknowingly ambiguous to himself and yet flatly unintelligible to the audience. And the key point is that this last situation is different from speech that is flatly unintelligible even to the speaker.
Consider: in such cases, the speaker confuses several different things unknowingly and uses the same words to describe these different things. (The speaker is unknowingly ambiguous to himself.) Yet the audience is often baffled and sees no way to construe the words intelligibly. (The speaker is, thus, unintelligible to the audience.) And in this circumstance (which is actually quite common), the audience can then easily suppose that the speaker must also be unintelligible to himself rather than just ambiguous to himself. The audience concludes that the speaker has no ideas, whereas, in fact, the speaker just has confused ideas. (Wittgenstein’s misstep, then, in our view, consists in mistaking a case of unknowing ambiguity to oneself for a case of unknowing unintelligibility to oneself.)23
Such, then, is our complaint with Wittgenstein’s conjecture. But however this may be, the larger claim we mean to defend is that logic can’t depend on language in the first place because language depends on logic. Language depends on conventions, and what makes a convention possible from the start are logical relations (since, without these relations, none of our conventions would have implications). Instead, the underlying nature of logic seems rather like the sublime of nineteenth-century romanticism: timeless, placeless, eternal, and with a foundation that is ultimately inexplicable. Or so we believe. When we try to see logical truths literally with the eye, we see nothing at all. Instead, we only see them—to use a phrase of Aristotle’s teacher Plato—with the eye of the soul.24
![]()
Aristotle had little use for this sort of talk.25 It was all too ethereal. Plato had used examples from the airy and peculiar world of mathematics, but Aristotle, despite his use of mathematical examples in logic, was steeped in the empirical. Nevertheless, in his own way, Aristotle reached a broadly similar result because he, too, left the ultimate nature of logical principles unexplained. For Aristotle, scientific argument always presupposes first principles, but first principles are things whose existence can’t be explained. On the contrary, all explanation, by way of argument, must presuppose first principles. And he treats at least some principles of logic (specifically, the law of contradiction and the law of excluded middle) in the same way; he treats them as things that all explanation must presuppose.26 And so the ultimate reason for their existence can only be passed over in silence—a thought echoed in the very last line of Wittgenstein’s famous Tractatus: “Whereof one cannot speak, one must be silent.” That is how Aristotle left the matter—in silence—even as the world he had carefully built for himself at the Lyceum collapsed.
The end of Aristotle’s world came with the demise of his pupil and sometime patron Alexander. Alexander had pushed his armies ever eastward, presiding over the deaths of thousands in countless pitched battles and hoping all the while to unite all the lands between himself and what he imagined to be the end of the world—the edge of the great river Ocean. But finally, on the plain of the Indus (in present-day Pakistan), he despaired. The losses had been terrible. The enemies before him seemed innumerable. And so he turned back. He led a bloody, terrifying retreat down the Indus and along the edge of the Indian Ocean until he finally reached Persia and then the city of Babylon in 323 B.C. At last, overcome by wounds or illness or poison (even now, the cause is disputed), Alexander passed away.
The Greek city-states stirred once more at the news of his death. We are told that Aristotle, brooding over his connection to Alexander and sensing danger, concluded he must flee. He remembered the execution of Plato’s friend and inspiration, Socrates, and he feared the Athenians might “sin twice against philosophy.”27 So he left his school in the hands of his student Theophrastus in the hope that it might survive and fled to Chalcis on the island of Euboea. There, in the following year at the age of sixty-three, Aristotle died.