The Laws of Contradiction and Excluded Middle
WE LIVE in an age that is prone to relativism, but so did the classical Greeks. Truth and falsity became matters of deep perplexity to them as they began to encounter other cultures through trade. As commerce accelerated and linked ever larger parts of the Mediterranean world together, the more sophisticated of the Greeks soon realized that what one society took to be true, another often took to be false. Many began to wonder, who can know for sure what is true—and what does “truth” even mean? As a result, alternative theories of truth began to proliferate in the 400s B.C., and a deep sense of relativism soon spread among intellectuals. Many Greeks recalled the aphorism of the fifth-century poet Pindar, “Nomos is king,” which is often rendered as “Law is king” but which can also be translated as “Custom is king.” Many came to think that truth was only custom, or perhaps it was nothing at all. No less than other human beings, Greek thinkers loved to generalize, and many passed easily from the commonplace that some things in life are relative to the more daring and controversial thesis that all things must be relative. Long before Pontius Pilate uttered the words, the question “What is truth?” had become a popular riddle.
It was against this sweeping expansion of relativistic views during classical times that Aristotle and the Stoics often did battle and tried to carve out niches of objective truth in logic, science, and ethics. (In ethics, Aristotle thought some actions were always wrong, no matter what, but he thought there were other actions where a true assessment would need to be imprecise. He characterized ethics as “true for the most part.”)1 The ideas of truth and falsity became philosophically interesting in the classical age—but also matters of much confusion.
In logic, the key battles often centered on the law of contradiction (that no proposition of argument can be true and false at the same time) and the law of excluded middle (that every such proposition must be at least true or false). Problems of truth had led many thinkers of the period to dwell on paradoxes and to conclude that perhaps there was really no secure truth at all except the changing sea of human opinions. Others stuck to the view that truth must be something more than opinion, however much our opinions may vary. But behind all these tendencies was a growing sense throughout the Greek world of profound and disturbing uncertainty.
PARADOXES OF TRUTH
Many Greeks had become burdened by a deepening feeling of drift. Socrates expressed some of this outlook when he said at his trial that what he really knew for sure was that he didn’t know.2 Earlier, the Sophists had stressed the mutability of custom, and the Greek historian Herodotus had amused audiences by contrasting the many differing notions of different peoples. (For example, Herodotus asserted that, in contrast to the Greeks, the ancient Persians often deliberated while drunk but then reconsidered their decisions when sober; but if they decided while sober, they always made a special point of reconsidering the matter while drunk.)3 Many societies have since tried to make sense of people’s differing customs—brought into collision by trade—and one consequence has been to reinforce an inclination to caution, circumspection, and tolerance for opposing views. But another effect, in many historical periods, has been to propel some of the more ambitious thinkers of an age into deep, metaphysical speculations about knowledge and reality, sometimes to the point of absurdity.
For example, some Greek thinkers came to the view that to call a thing true is only to say that one happens to believe it: “It’s true because I think it so.” Others insisted that something is true only because the majority believes it or because those in power believe it. Still others held that everything is both true and false at the same time. These doctrines notwithstanding, some maintained that nothing is true or false; instead, everything falls into an intermediate middle ground: there are no truths or falsehoods in the first place, only opinions. An extreme version of this outlook was attributed to the fifth-century thinker Cratylus, who concluded that nothing could be truly asserted of a world in constant flux and who finally decided to stop speaking; instead, when questioned by his disciples, he only moved his finger to indicate that he had heard the question but found it impossible to reply.4
And many ancient Greeks clung to these speculations even though many other ideas seem to depend crucially on the difference between the true and the false. For instance, what is lying if nothing is true? What does it mean to misstate or misread or misrepresent? What is inaccuracy? In addition, whatever answers we give to these questions, what happens if we ask whether our answers are themselves true? Can it be “true” to say that nothing is true? Perhaps we could escape such conundrums by falling back on the theory that nothing is absolutely true; yet how do we then explain the difference between the absolute and nonabsolute if we can’t even say outright that something is true? Maybe we could avoid difficulties of this kind by confining ourselves merely to approximating the truth, but how do we then explain the thing we are approximating? Do we approximate a thing even though there is no such thing in the first place?
Aristotle’s predecessors had already encountered many of these problems, some of which came out in one of Plato’s classic dialogues, the Theaetetus. It includes a discussion of the doctrine of the Sophist Protagoras, whose treatise Truth had asserted, “Man is the measure of all things.” The exact meaning of Protagoras’s utterance has long been disputed, but Plato took Protagoras’s words to mean that anything is true so long as the majority believes it—a doctrine Plato challenged. The doctrine seemed to make the majority infallible except when the majority ended up denying the doctrine itself (in which case it became self-contradictory).5
In sum, many Greeks of the classical age had sought an analysis of truth that was forbearing and cautious and wound up instead with something metaphysical and ponderous. New schools of philosophers then emerged to propound these unusual ideas. For example, the ancient Skeptics, who flourished shortly after Aristotle and adopted an outlook much like Cratylus’s, insisted that all things in life were unknowable.6 Another group, the Cynics (meaning “doglike”), lived in hovels and begged for food and insisted that the only real truth involved renouncing human convention. (The most famous Cynic was Diogenes of Sinope, a man of pungent wit who lived in a large storage jar or “tub.” He mocked at the conceits of the world, and when approached by Alexander the Great, who stood over him to inquire whether he needed anything, replied, “Yes, stop blocking the sunlight.” Plato is said to have remarked of Diogenes, “That man is Socrates—gone mad!”)7
In capturing the real nature of truth, perhaps the simplest approach would have been to say that the truth is often hard to discern, but many thinkers of the ancient world chose a different path: deny all truth, all knowledge, and all certainty. And they did so, even though the practical problem, usually, was to determine which things were true, which were known, and which were more certain or less so. (A doctrine of truth that assigns the same status to all propositions indiscriminately is no help in distinguishing any of them in particular; it tells us nothing about how some ideas differ from others.)
Aristotle viewed many of these old doctrines of truth with hostility; he regarded them as half-examined crudities and thought they could only be believed by people who were incapable of following out the logical implications of their own ideas. His impatience sometimes spilled out on the page. In his Metaphysics, remarking sarcastically on the doctrine that everything is both true and false at the same time, Aristotle argues that no man who thinks he ought to do something then proceeds not to do it on the grounds that he also ought not to do it: “Why does a man walk to Megara and not stay at home when he thinks he ought to be walking there? Why does he not walk early some morning into a well or over a precipice? Why do we observe him guarding against this—evidently because he does not think falling in a well is alike good and not good.”8
Despite Aristotle’s impatience, many of the old doctrines of truth have continued down to modern times, and many arguments still adduced on their behalf are actually ancient Greek arguments. For example, here is the nineteenth-century Marxist philosopher Friedrich Engels arguing that all propositions are both true and false at the same time, and doing so by invoking a version of an ancient Greek paradox of the fourth century B.C. called the “bald man”: “Whether an animal is alive or not . . . is, in many cases, a very complex question. . . . It is just as impossible to determine absolutely the moment of death, for physiology proves that death is not an instantaneous, momentary phenomenon, but a very protracted process.” From this, Engels concludes that dying animals are both alive and not alive, and that everything “is and is not.”9 In the ancient version of the paradox, we are asked to determine not the moment of death but the moment at which a hairy man, who loses his hairs one by one, becomes a bald man. Since it is difficult to draw any precise line between baldness and hairiness, it seems that hairy men are bald and not bald.10
As it happens, the truth and falsity of all propositions became a staple of orthodox Marxism because Marx and Engels had both inherited this creed from the German philosopher G. W. F. Hegel, who was popular when they were students and who drew much of his inspiration from the many paradoxes of early Greek philosophy. Here is Engels again, but this time making a different argument for the truth and falsity of all things: “Every organized being is every moment the same and not the same; every moment it assimilates matter supplied from without, and gets rid of other matter; every moment some cells of its body die and others build themselves anew; in a longer or shorter time the matter of its body is completely renewed, and is replaced by other molecules of matter, so that every organized being is always itself, and yet something other than itself.”11 This time the argument is a version of another Greek paradox: the ship of Theseus. According to the ancient story, the Athenians preserved the ship of their famous early king Theseus, who had united Attica, fought the Amazons, penetrated the Labyrinth, killed the Minotaur, and endured many other adventures. But as the ship gradually decayed, the Athenians replaced its various parts one by one. Eventually, all the ship’s parts had worn out and been replaced. So the question arose, was it still the ship of Theseus? The answer, according to some of the ancients, was that it was the ship, and yet it wasn’t the ship.12
Many arguments of this sort—everything is both true and false—turn on ambiguous phrasing. In the last passage from Engels, for example, the phrase “the same” is ambiguous. An object can be “the same” in some respects (still alive) yet different in other respects (e.g., assimilating a particular molecule at one moment and expelling it the next). This is different from showing that an object is simultaneously “the same and not the same” in the same respect, which is the conclusion that Engels wants to draw. If the object is the same in respect to being alive but different in respect to assimilating a particular molecule, then we could still have two propositions here, one of which might be true and the other of which might be false. Engels wants to show that there is just one proposition, which is true and false simultaneously. (In the case of the ship of Theseus, the ship can be “the same” in terms of form but different in terms of matter.)
Other such arguments turn on vagueness.13 In Engels’s earlier argument, he contends that it is impossible to determine absolutely the moment of death; the point of death is sometimes vague. Considered carefully, however, all that this observation actually shows is that the moment of such a death is, as Engels says, indeterminable. It is quite another thing to say that the same being is both dead and not dead. By analogy, if we can’t determine whether our employer plans to fire us, then it hardly follows that he both plans to fire us and does not plan to fire us. Instead, all that follows is that we can’t yet determine his plans. There are many such arguments about truth, and many turn out, on examination, to depend on a hidden non sequitur.
Here is yet one more of these old doctrines of truth, this time a recycled version of the thesis of Thrasymachus, an ancient Greek Sophist who was depicted in Plato’s Republic. Thrasymachus maintained that justice is nothing but the “interest of the stronger party.”14 He seems to have meant that justice is whatever happens to serve those who hold political power. In the ancient version of the doctrine, power determines justice, but in the modern version, power determines truth—or so says the French social thinker Michel Foucault. Foucault’s phrasing is sometimes convoluted, but his dictum still circulates broadly through academia and still represents an echo of the ancient Thrasymachus. The basic idea isn’t hard to get. Foucault says those in power create a “discourse,” and, by controlling and dominating this discourse, they also create truth: “In any society, there are manifold relations of power which permeate, characterise and constitute the social body, and these relations of power cannot themselves be established, consolidated nor implemented without the production, accumulation, circulation and functioning of a discourse. There can be no possible exercise of power without a certain economy of discourses of truth which operates through and on the basis of this association. We are subjected to the production of truth through power and we cannot exercise power except through the production of truth.” He continues:
Each society has its regime of truth, its “general politics” of truth: that is, the types of discourse which it accepts and makes function as true. . . . “Truth” is centered on the form of scientific discourse and the institutions which produce it . . . it is produced and transmitted under the control, dominant if not exclusive, of a few great political and economic apparatuses (university, army, writing, media). . . . “Truth” is linked in a circular relation with systems of power which produce and sustain it, and to effects of power which it induces and which extend it.15
The doctrine, though wordy, turns partly on an ambiguity. If by a discourse we mean a vocabulary, or perhaps rules of usage, then it makes little sense to ask whether such things are “true.” (Asking whether a vocabulary is true is like asking whether the English and French languages are true; the question is nonsense.) On the other hand, if by a discourse we mean a series of assertions that use the vocabulary—so that no one can assert as true anything that those in power deny—then Foucault’s doctrine would seem to defy common sense.
Consider: if we use the words of the discourse to deny the assertions of the controlling and dominating people who teach them to us, then either our statements are true or theirs must be true. This much seems to follow from the law of excluded middle (if we are willing to take the law for granted) and from the fact that we “deny.” On the other hand, suppose we assume nothing here except that we can never even deny the assertions of those dominating people because they supply us with our words. In that case, we might just as well argue that small children will never deny any assertions of their parents on the ground that the parents who control and dominate them have taught them their words. After all, in the first years of life, children are subjected to the most intense form of domination and control (and the most intense “discourse”) in all human experience; yet most parents learn eventually that their children will indeed deny what they say.
Speaking truth to power is surely hard; people with power sometimes use threats and sophistries to suppress the truth. But Foucault’s argument, taken literally, would really show something different: speaking truth to power is impossible anyway since there can be no truth without power. The doctrine implies that those in power can never have true reasons for thinking themselves mistaken, since they control the discourse. The doctrine belies the common experience of hearing oneself contradicted (something that happens even to the most powerful and arrogant), but it is also remarkably defeatist; it implies that the powerful can never be contradicted. (Alternatively, many thinkers have tried to avoid such objections by redefining the word “true,” such that a proposition becomes “true within a discourse” if it is logically consistent with—or coheres with—all other propositions in that discourse, or with the “rules of the discourse.” But the trouble with all these tactics is that they succeed in redefining truth only at the price of making the definition circular. To call two things “consistent” is to say that both can be true at the same time. Thus, far from banishing some earlier notion of truth, these tactics seem to presuppose one.)
The task of the early Greek logicians was to cut through obscurities and confusions of this kind and to arrive at the ideas of truth and falsity that regulate reasoning in the ordinary sense of the word. Remember that logic is the study of arguments, and an argument, to a logician, is an attempt at proof. In that case, however, no matter how uncertain our various opinions may be at any one time (or in any one historical period), argumentation will be useful only under particular conditions. Logicians in many ages have described these conditions, sometimes in varying ways, but the account we give now is not much different from accounts given by others, whether by Aristotle or by those who came after. We shall specify three such conditions (under the headings of “truth as independent of opinion,” “the law of contradiction,” and “the law of excluded middle”):
1. Truth as Independent of Opinion
First, no proposition we argue about can be true just because we believe it. Instead, its truth must turn on something more than the mere fact of our conviction; otherwise, the argument is unnecessary. If a proposition is true simply because we believe it, then why reason about it in the first place? The belief becomes necessarily true, and in that case we can dispense with the hard work of assembling evidence and distinguishing the valid from the invalid. (To say this isn’t to deny that some propositions are true simply because we believe them. For example, the proposition “I am thinking” becomes true if one believes it—one’s thinking it makes it so.16 But matters of argument need to fall outside this category. The first assumption of argument, then, is that not everything is true simply because we believe it.)
Notice that similar observations apply to the idea that a proposition is true simply because society believes it, or because a majority believes it, or because those in power believe it. In that case, society, the majority, or the collection of powerful personages becomes infallible in the sense that their belief in the proposition is necessarily true. Criticism assumes, on the contrary, that those with whom we argue might be mistaken and the attempt to persuade them by reasoning assumes that the person to be persuaded doesn’t yet realize something true.
The experience of the ancient Greeks showed that there could be many theories of truth, and in the centuries that have followed, truth has been variously described as objective, subjective, intersubjective, relative, pragmatic, performative, eliminable, dependent on correspondence with reality, dependent on coherence with other accepted beliefs, dependent on coercion and power, and so on. But another legacy of the Greeks, derived from their logicians, is that such theories are largely irrelevant to logic. Historically, theories of truth come and go, but the results of logic have remained. Though there have been many theories of truth, the validity of modus ponens—at least in ordinary cases—has always been obvious. (As for the extraordinary cases, sometimes debated by professional logicians, we shall be talking about these in a short while.)17 As long as the expressions “true” and “not true” are intelligible and as long as the proposition to be proved doesn’t hinge on the mere belief of the person to be persuaded, one’s preferred theory of truth makes little difference. (On the other hand, if the expressions “true” and “not true” are not intelligible, then no theory of truth will be helpful anyway, since no one will know what the theory is about.)
An analogy to arithmetic might also be useful. In arithmetic, we add and subtract numbers, but what is a number? Is it a physical object? Is it only an idea in our heads? Is it an abstract, mathematical entity—among infinitely many other such entities—that exists even if no one thinks about it? (Mathematicians say there are infinitely many numbers even between one and two, but who has infinitely many ideas in his head?) Explaining what a number is turns out to be philosophically difficult. Nevertheless, no one would say that we can’t do arithmetic unless we can also answer these metaphysical questions about numbers. Just so, to distinguish valid arguments from invalid ones we must still ask whether the truth of a conclusion follows necessarily from its premises. But in ordinary circumstances this no more requires a general theory of truth than adding five and seven requires a general theory of numbers. (All the world’s languages have expressions for true and false, and in logical matters there will still be some clearly right answers and some clearly wrong ones.)
2. The Law of Contradiction
Arguments, to be useful, must also meet a second condition: No proposition of argument can be both true and false at the same time (“false” meaning “not true”).For many centuries, this assumption has been called the law of contradiction.18
The justification of the law is practical. If a proposition is both true and false, then it refutes no errors. But in that case, why is the proposition worth arguing about—or even worth knowing? It disproves nothing. (To refute an error is to show that it is not true, but the trouble with contradictions is that they allow what is false to be true nonetheless.)
In most systems of formal logic, a contradiction (meaning a statement in the form “A and not A”) is false since, if true, it would imply that the same proposition was true and false simultaneously.19 All the same, there have long been objections to the law of contradiction, and most come from construing the law as something more than it is: as a theory of physical reality, of how to live one’s life, or of how to order one’s mind. Often, objections to the law derive from the perfectly reasonable complaint that logic is sometimes oversold; not everything in life is a matter of logic.
Let’s take a moment to elaborate this complaint: Some things in life can only be felt to be appreciated, and some things are better left unanalyzed and spontaneous. If we then insist on reducing everything to premises and conclusions and consistent descriptions, sometimes we simply fail to grasp it. In fact, maybe the most important things in life have nothing to do with reason and logic. Themes such as these are common in nineteenth-century romantic literature; Walt Whitman writes, “Do I contradict myself? / Very well then I contradict myself / (I am large, I contain multitudes).” The Tao Tê Ching often uses similar language,20 and even so eminent a logician as John Stuart Mill warns against the “dissolving influence of analysis.”21 Emerson insists, “A foolish consistency is the hobgoblin of little minds.” In some matters, if we demand logic and nothing but, we merely become too clever by half. In other words, uttering contradictions and defending them is actually a perfectly coherent way of saying that the subject isn’t really a matter of logic at all. Nevertheless, the key point here (sometimes overlooked) is that logic’s approach to contradictory utterances extends not to all their linguistic uses but only to their use as expressions of an argument’s elements—its premises or conclusion.
Strictly speaking, the traditional law of contradiction, construed as a principle of logic, applies only to the parts of an argument or inference. It tells us what must be so to the extent that the world can be known by inferring some propositions from other propositions. (Logic assumes that the world cannot behave in logically impossible ways, but if the world does so behave, then the behavior is simply beyond logical comprehension.)22 Nevertheless, this is not a theory of how to live one’s life. Nothing in the principle, taken literally, indicates whether we would be better off if all our beliefs were rigidly consistent. If a person maintains contradictory beliefs, then logic tells us that at least one of those beliefs must be false. (This much follows from the law of excluded middle on the assumption that the beliefs in question can be propositions in the first place.)23 But nothing else follows whatever. Does this person know more or less than other people? Would this person’s life be better if his beliefs were revised? Should this person’s judgment be generally trusted or generally discounted? On all these further questions, logic as a discipline is strictly silent. We don’t deny that such further questions have answers, but any complaint about the answers isn’t really a complaint against logic but against something that has been mistaken for logic. The complaint is against a further theory of the mind or of the good life—or of social organization.
In practice, contradictions are often used in ordinary language to assert that a subject isn’t really a matter of argument but a matter of feeling or intuition. This is the use often made by romantic writers and perhaps also by the Tao Tê Ching. Contradictions can also be used to express the absurd or the hopeless. All the same, the tendency to overstate logic’s province and to imagine the law of contradiction as a grand principle independent of argumentation has deep roots.
As a matter of history, many of our current attitudes toward logic and rationality come down to us from the eighteenth-century European Enlightenment, when many writers insisted on reason as an instrument of social reform. Many of them seemed to assume that Reason (capitalized) was the only thing that mattered. In this respect, the romantic movement that followed may have been a valuable corrective. In fact, no principle of logic, properly understood, contradicts any of the classic romantic themes. Nevertheless, this natural tension between romanticism and the Enlightenment has been translated more recently into an imagined tension between East and West, between “Eastern logic” and “Western logic,” and this further supposed tension is fictitious.
So far as history goes, there has never been any particular Eastern or Western view of contradiction, nor any sort of Eastern logic incompatible with a Western one—nor any “male logic” as opposed to a “female logic.” Of course, the word “logic” can be used loosely to indicate a mere set of opinions or customs, or perhaps a collection of mannerisms and tendencies; but if by “logic” we mean the practice of the most common methods of rational inference, then the theory that there are Eastern and Western logics, or male and female ones, is fantasy. There are no more Eastern and Western logics than there are Eastern and Western arithmetics. Consider this simple argument that embodies modus ponens:
If you don’t eat tomorrow, you’ll be seriously weakened.
You won’t eat tomorrow.
Therefore, you’ll be seriously weakened.
In the sad saga of human experience, has the validity of this inference ever been less apparent to peoples of the East than of the West, or to women than to men?
Of course, Aristotle explored a great many other forms when he examined syllogisms, so perhaps one could say that syllogistic reasoning is the special mark of the Western mind. But this, too, seems to be mistaken. In practice, people in the West have made no more use of syllogistic forms than people in the East; in fact, except for the Barbara syllogism24 and a few others, nobody really uses syllogisms at all—except logicians. Might it still make sense to say that Aristotle’s theory constitutes a distinct “Western logic” on the grounds that it was first developed by a man we now call Western? (If so, we should call the differential calculus “Anglo-Germanic mathematics” on the grounds that it was first developed by an Englishman and a German: Isaac Newton and Gottfried Leibniz.) But permit us to complain just a bit more, this time on behalf of classic literature of the East.
The Tao Tê Ching stresses themes of spontaneity, mystery, nonaggression, and acceptance, and it does this by contradictory utterances. We might ask, don’t these literary qualities still count, in some sense, as a distinct Eastern logic? The trouble with this view is that the same themes appear in much Western literature, and the defense of contradictions has a long Western pedigree (it goes back to Aristotle’s predecessors).25 In consequence, if a love of contradiction were the special mark of a distinct “logic,” it would make more sense to call the defense of contradictions a divergent “Western logic.” In addition, this East/West approach steadfastly ignores the great diversity among Eastern classics themselves, many of which turn out to be rigidly consistent and analytical. (Among these consistent and analytical texts are Kautilya’s Arthasastra from India, perhaps of the fourth or third century B.C., which might well be mistaken for a work by Machiavelli, the writings of the third-century Legalist Han Fei Tzu of China, and Sun Tzu’s Art of War. The Analects of Confucius don’t contain any obvious examples of intended contradiction either. Ancient Chinese thinkers were often acutely sensitive to the accusation that they had contradicted themselves.)26
In sum, this attempt to distinguish a monolithic Eastern view, different from an equally monolithic Western one, belies the literary diversity of both regions. The attempt ignores what the classics of both regions really look like.
3. The Law of Excluded Middle
Useful argumentation must also meet a third condition: Every proposition of argument must be at least true or false. (For example, either it is true that today is Tuesday, or it is false that today is Tuesday.) Traditionally, this is called the law of excluded middle.27
This principle differs from the law of contradiction in that the earlier law asserts that truth and falsity are mutually exclusive, whereas the law of excluded middle implies that together they are exhaustive. That is, while the earlier law says truth and falsity are incompatible, this new law says that together they complete a list of possibilities. The law of excluded middle does indeed allow that a proposition might have any number of different characteristics—maybe five, maybe ten, or maybe more—but it requires that the proposition have at least one of these characteristics: truth or falsity.
As with contradiction, the justification of the law is practical. Many things in life are neither true nor false, and many things seem somewhat true, or their truth is hard to assess. Nevertheless, if a premise of an argument is neither true nor false, then the premise proves nothing. (Imagine, for example, someone saying, “I believe this conclusion for a good reason, but my reason is neither true nor false.”) On the other hand, if the conclusion of an argument is neither true nor false, then no argument can prove it. (In ordinary language, what would it mean to “prove” the untrue?)
Many objections to the law come from construing it as something more than it needs to be, as a theory of life or of the physical world. Instead, strictly defined for the purposes of logic, the law applies only to the specific objects of logic—to premises and conclusions of argumentation in the ordinary sense.
Historically, the law of excluded middle has been much discussed and often disputed. The ancient Epicureans denied the law outright, and a similar outlook was embraced by a number of medievals; in modern times, the American pragmatist C. S. Peirce experimented with alternatives to true and false, and the Polish logician Jan Łukasiewicz explored the possibility that the list of alternatives to true and false might be infinitely long.28 When a logician has in mind only two values, true and false, the resulting system is “two-valued” or “binary”; but when the logician allows for three possibilities, true, false, and indeterminate (or, as some medievals called it, “neuter”), the resulting system is “three-valued.” And Łukasiewicz investigated a “many-valued” logic with the consequence that more than a few logicians and mathematicians now speak routinely of many-valued logics, especially when seeking ways for a computer to assess vague or incomplete information. They also apply the word “fuzzy” to this area of research, and so there now exist fuzzy logic and fuzzy set theory, both involving precise definitions and rigorous methods.
Fuzzy set theory, proposed by the mathematician Lotfi Zadeh in 1965, posits a set whose elements are members only to a certain degree.29 For example, a person in late middle-age might be conceived as only somewhat a member of the set of the elderly. Fuzzy logic (also explored by Zadeh) then goes a step further by assigning degrees of truth to such statements. Thus, in fuzzy logic, it is somewhat true that a person in late middle-age is a member of the set of the elderly. Fuzzy logic can be treated as a branch of many-valued logic, and in both fuzzy logic and fuzzy set theory the degrees of truth or membership can also be assigned numerical values so they can be treated mathematically. But here’s the strange part: all these investigations still rely on the same traditional principles we have already considered: the law of excluded middle and the law of contradiction. How can this be?
THE NATURE OF FUZZY LOGIC
The simplest way to answer this question is to indulge for a moment in a little fuzzy logic of our own. Take a simple example. We often remark that a particular assertion strikes us as “somewhat true.” The remark is vague, and many people, if they have time, will investigate the assertion to seek out true parts and false parts or true interpretations and false interpretations. Nevertheless, the remark is by no means irrational; it faithfully reports our feelings of vague belief or confusion. Of course, it would make little sense to offer this same assertion as a reason for believing something to be true. (“My view is true, and the reason I know it is true is that it follows from something that is somewhat true.” Notice that even Aristotle acknowledges that generalizations in ethics are often “true for the most part,” yet he also adds that a premise so qualified can only support a conclusion that is so qualified.)30
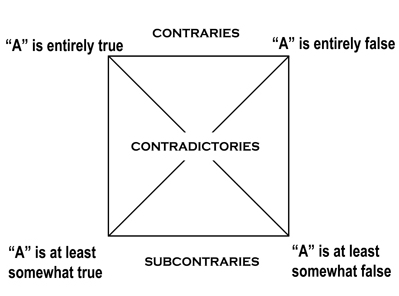
Despite this difficulty, however, we can still draw a good many inferences about the assertion in question, even if we can never bring ourselves to call it any more true than “somewhat.” For example, if an assertion is “somewhat true,” then it can’t be “entirely false.” On the other hand, if it is “somewhat true,” then it could also be “somewhat false.” In addition, depending on what we mean by “somewhat,” the assertion might be entirely true. (If by “somewhat true” we mean “at least somewhat true,” then it is perfectly coherent to say that an assertion is “at least somewhat true and maybe entirely true.”)
In consequence, we can generate something like the traditional square of opposition. (See figure 5.1.)
We could easily call this a four-valued logic. Our inferences have involved not the usual two values of true and false, but four values: “entirely true,” “at least somewhat true,” “at least somewhat false,” and “entirely false.” And these assignments of value have logical implications of their own, which turn out, in this instance, to replicate what we saw earlier in the traditional square. (The first and last values, “entirely true” and “entirely false,” are logical contraries; the first and third values, “entirely true” and “at least somewhat false,” are contradictories; and so on.)
Construed in this way, the assertion that we are evaluating (“A”) can have more than one value at the same time, and this would be analogous to denying the traditional law of contradiction in the old two-valued system; but we can also eliminate this feature if we find it disturbing by reducing the values of the system to three mutually exclusive possibilities: “entirely true,” “only somewhat true but also somewhat false,” and “entirely false.” (Now the assertion can have only one of the values.)
All the same, what we see throughout is that a many-valued system will still involve logical implications of its own, which is just the point that Łukasiewicz was investigating. (In practice, the values in a system of many-valued logic might be as varied as “is slightly true,” or “is fifty percent true,” or “is necessarily true,” or “is possibly true,” or “is true in Euclidean and Riemannian but not in Lobachevskian geometry.”) Nevertheless, the key point here is that at no time in these manipulations have we ever violated the law of contradiction or the law of excluded middle.
Here’s why: We have surely been willing to assign three or four possible values to the assertion “A,” but at no time did we invoke this assertion “A” as a premise or conclusion in our reasoning. Instead, our premises and conclusions were statements about the assertion. That is, our premises and conclusions were in the form, “The assertion ‘A’ is somewhat true” or “The assertion ‘A’ is not entirely false.” In other words, our premises and conclusion weren’t simple statements like “A” but statements about those statements—what logicians call “metastatements.” (A metastatement is a statement about a statement.) And all our metastatements were treated as true or false but not both.
Let’s put this point generally: however many values we might assign to a proposition in drawing inferences of this type, the assumption we make from the start is that the proposition does indeed have such a value or it doesn’t. And we also assume that the proposition doesn’t simultaneously have that value and not have that value. These two assumptions represent the stamp of the two ancient laws. We regard the assignments of value as being themselves true or false but not both. On the other hand, if we relax these assumptions and violate them, then we can draw no reliable inferences at all. In that case, either our assignments of value become indefinite or they result in contradictions. Put another way still, many-valued logic seeks to describe the relations that hold among assertions that fail to qualify as exclusively true or false, but it still tries to describe these relations truly. And it tries to arrive at this description by logical argument, from true premises. Thus, to succeed, it still conforms to the same principles that govern logical argument in every other field.
On this view, many-valued logic isn’t an alternative to ordinary logic but only a further application of it—to propositions that don’t qualify as “argument” in the usual sense of the word. (Still another way to express this point might be to say that, though logic studies an activity, the activity of reasoning, this activity is made possible by things independent of the activity: logical relations themselves. Thus logic focuses on our efforts, but it leads us to things that are independent of those efforts, to a world of abstractions. And many-valued logic studies yet another part of that mysterious world. Nevertheless, logical argument in the ordinary sense remains the window through which we see it.)
In recent years, professional logicians have developed a great many alternative logical systems of this sort, systems analogous to Łukasiewicz’s version of many-valued logic or to Zadeh’s fuzzy logic. Many of these systems assign values different from the traditional “true” and “false,” and they can also employ rules of inference that differ from one system to the next—with the effect that a valid argument according to one system can turn out to be invalid according to another. (Some of these systems happen to be called “deviant logics” or “nonclassical logics.” A “logic” in this sense is a formal system in an artificial language, and with differing values and rules, these systems can have differing logical consequences; recent examples include additional fuzzy logics, relevance logics, intuitionist logics, and paraconsistent logics.)31 Nevertheless, the coherence of these systems still depends on the same two assumptions: a proposition being evaluated does indeed have the assigned value or doesn’t and can’t both have the value and not have the value. (Otherwise, the system becomes incoherent.) Once again, we see the stamp of the two ancient laws.
But here, perhaps, is a more basic question (or at least a question that could be posed for the sake of argument): If different logical systems can generate different results—and count the same argument as valid or invalid, depending on the system—then isn’t the validity of an argument just relative to a system? Doesn’t an argument’s validity really depend on which logical system one has in mind? And if one system should then turn out to be just as good as another, isn’t the validity of an argument arbitrary?
IS VALIDITY RELATIVE?
Notice that if by a “logic” we mean one of these formal systems in an artificial language, then men and women don’t normally have different logics, and neither do different cultures. Instead, the only people who have different logics are professional logicians (and their students) because these are the only people who study such systems in the first place. Nevertheless, couldn’t we still say that the existence of these systems shows that all questions of validity are really just relative to a system? What counts as valid (we might suppose) depends on which system you have in mind.
As it turns out, the great majority of these formal systems give the same answers when it comes to determining the validity of commonsense reasoning in ordinary life, and if they didn’t, they would appear flatly absurd. Different systems construe the precise form of commonsense arguments in different ways (and translate them differently into artificial languages), but they usually provide some explanation as to why each of these commonsense arguments is valid nonetheless (as when dealing, for example, with an argument like, “All men are mortal, and Socrates is a man; therefore, Socrates is mortal”). Instead, the differences between these systems show up only when their rules are extended to esoteric cases.32
For example, consider this argument: “Lincoln never lived; therefore, either the week has seven days or it does not.” Is the argument valid? In some logical systems this argument is counted as valid on the grounds that it can never have true premises and a false conclusion; its conclusion is necessarily true. In other systems (particularly those called “relevance logics”), the argument is invalid on the grounds that the premise has no real connection (no relevance) to the conclusion.
Or consider this example: “If John is in Paris, he is in France, and if John is in London, he is in England. Hence it is the case either that if John is in Paris, he is in England, or that if he is in London, he is in France.” (In a relevance logic, this argument would be counted as invalid, and yet in the symbolic system now called “classical logic,” the argument seems to be valid after all; the system called classical logic is not a logic of classical antiquity but, rather, a formal system first developed by Gottlob Frege and then refined by Bertrand Russell and Alfred North Whitehead. We shall be talking more about the development of classical symbolic logic in chapter 9, and this argument appears to be valid in classical logic because of the way classical logic treats the conditional “if-then.”)33
All the same, whoever is right about these unusual cases, the arguments in question are exotic from the start. They don’t come from everyday reasoning but from logicians themselves (whose purpose is to demonstrate the inadequacy of a system developed by other logicians). Only in these esoteric domains does a choice of one formal system over another truly make a difference. And the key point is that no one really needs such a system in the first place to assess the validity of countless commonsense examples or to distinguish ordinary logical principles and ordinary logical forms.
By analogy, we often invoke physical principles in ordinary life, and we distinguish different forms among physical objects, even though the forms have borderline cases and even though the principles admit of unusual exceptions. For example, the principle “If you jump from an eight-story building, you will die” is normally true. Yet there can be exceptions to the principle, as when a safety net is erected or when an aircushion is deployed by a stunt artist.
Again, when it comes to physical forms, we can distinguish Homo sapiens as a matter of form from other primates, just as we can distinguish modus ponens as a matter of form from other kinds of arguments. Nevertheless, there can be borderline cases of the form, as when an expert examines the fossilized remains of an early, hominid ancestor. More generally, it is often reasonable to invoke a principle even though no one is quite sure of the exact extent of its proper application, and one can distinguish different forms of things even though no one is quite sure how to judge a borderline case.
It is just so in logic. Modus ponens and the disjunctive syllogism are perfectly valid forms of argument in ordinary contexts, and each can be viewed as a principle for logically inferring some propositions from others. Nevertheless, these forms can also be matters of plausible dispute when applied in esoteric contexts. (In nonclassical logics, both modus ponens and the disjunctive syllogism are sometimes treated as invalid.) In short, disputes in the esoteric cases do nothing to show the inadequacy of such principles in ordinary cases. And in ordinary situations, our knowledge of which arguments are valid and which principles are logically sound is quite independent of any of these systems. (After all, if our knowledge weren’t independent, then no one would know anything at all about logic except those few logicians who had happened to hit upon the right system. The true subject matter of these systems is esoteric from the start.) Though the exotic cases are often baffling, the commonsense ones are clear.
DOES FORMAL LOGIC ULTIMATELY DEPEND ON COMMON SENSE?
Nevertheless, why fall back on “common sense” in the first place? Indeed, isn’t it still a mistake (one might wonder) to place so much confidence in “common sense”? In fact, couldn’t one of these advanced systems still overthrow what we normally think of as common sense? And in that case, couldn’t one still say that what counts as valid is ultimately relative to a system?
Let’s carry this objection just a bit farther (at least for the sake of argument): Common sense, as the saying goes, is not so common. And many things called common sense have later turned out to be utterly false, especially in science. For example, it used to be “common sense” that the earth does not move, because no one feels it moving, and yet modern science has overturned this idea. By analogy, then, couldn’t an advanced system of formal logic also overturn some of one’s commonsense beliefs about what is logically valid and what isn’t?
Of course, anyone’s judgments in logic are apt to be mistaken sometimes; everyone makes logical mistakes from time to time, even logicians (just as everyone makes mistakes in arithmetic). And in consequence, one’s abilities in logic (as in arithmetic) can certainly be sharpened; if formal logic never changed one’s judgments, there would little point in studying it. But it would be quite another thing to say that formal logic might overthrow commonsense beliefs to the same extent that physical theories have overthrown commonsense beliefs.
On the contrary, a theory of physical science is quite unlike a formal system of logic.
Specifically, physical theories can overturn commonsense beliefs because of an additional factor: the theories can be supported by empirical tests and experiments. They can result in testable predictions, and the truth or falsity of the predictions can be physically observed. By contrast, a formal system of logic doesn’t seem to be empirically testable at all, or, if it is, the tests are deep and remote. (Quantum mechanics is sometimes thought to generate physical counterexamples to the law of excluded middle, but this contention is much disputed, and, even if granted, the contention would seem to have no bearing on the law when used in ordinary situations. Once again, the consequences would be esoteric.)34 History includes many empirical tests in physics and astronomy, but no one knows how to test a formal logical system as one might test the Copernican hypothesis or Galileo’s law of falling.
Still, why not push the objection to “commonsense” reasoning (one might wonder) even further—to its logical extreme?
What if logicians were to invent an alternative system of logic that was so different it contradicted most commonsense judgments of validity, even those that seem most obvious? In other words, couldn’t we at least imagine adopting a different system of logical rules, even in ordinary contexts, and thereby abandoning what we normally think of as commonsense reasoning? And if we can imagine this possibility, doesn’t it then follow that our confidence in commonsense reasoning is actually unfounded and that the choice between one sort of logic and another is arbitrary after all?35 Philosophers have often been deeply skeptical about other things; why not be just as skeptical about ordinary logic?
Now, in considering these last possibilities (and entertaining them once more for the sake of argument), perhaps it would be useful to think about optical illusions—where one can pose similar questions about what is truly well founded and what is really just arbitrary.
Our physical senses sometimes deceive us. We sometimes make mistakes about the causes of our sensations. We are fooled by mirages, and a professional conjurer can sometimes make us doubt the very testimony of our eyes. And from these commonplace experiences, skeptical philosophers from ancient times to the present have sometimes argued that we don’t even know that we have hands and feet. Instead, we have no way of knowing (so they say) that the whole world isn’t just a dream, or an illusion, or the work of an “evil spirit, no less clever and deceitful than powerful, who has bent all his efforts to deceiving us.”36 Our belief in the physical world (these philosophers say) is arbitrary from the start.
It takes no great leap to see the similarity between these old skeptical arguments about physical reality and our new skeptical arguments against ordinary logic. If the possibility of an alternative logic is a good reason for doubting ordinary logic, then the possibility of an alternative reality is a good reason for doubting the existence of the physical world.
When it comes to the physical world, the twentieth-century English philosopher G. E. Moore once offered what he regarded as a “perfectly rigorous proof” of its existence. He said he could generate his proof “by holding up my two hands, and saying, as I make a certain gesture with the right hand, ‘Here is one hand,’ and adding, as I make a certain gesture with the left, ‘and here is another.’” His point was that the existence of our hands is already so obvious that any philosophical argument against it is more likely to be mistaken than our commonsense belief. In a similar vein, Samuel Johnson is said to have challenged the skeptical idealism of philosopher George Berkeley by kicking a stone and remarking, “I refute it thus.”37
Our approach is like Moore’s, except that we refer to simple judgments of logic and arithmetic in place of judgments about the physical world. Do we have any less assurance of the validity of modus ponens in ordinary cases than we have of the existence of our hands?
Writing in the eighteenth century, the Scottish philosophy David Hume remarked, “Excessive principles of skepticism . . . may flourish and triumph in the schools, where it is indeed difficult, if not impossible, to refute them.” He added, “But as soon as they leave the shade . . . they vanish like smoke.” As soon as the skeptical philosopher confronts a real problem of life, like finding a meal, obtaining drink, getting shelter, or determining the correct mathematical sum of his or her bank account, the philosopher reasons just like the rest of us. “The first and most trivial event in life will put to flight all his doubts and scruples, and leave him the same, in every point of action and speculation, with the philosophers of every other sect.”38 Hume observed that even the most ardent philosophical skeptic, when the lecture has ended, still leaves by the door and not by the window.39
Just so in logic. In ordinary affairs, even the most skeptical and deviant logician must still draw inferences like other people—or perish. We can certainly imagine reasoning differently, and we can imagine doubting ordinary logic, but imagining that we are doubting is not actually doubting. (Imagining that we doubt is no more a form of doubting than imagining that we fly is a form of traveling from place to place.) The argument from what we can imagine confuses two very different psychological states: doubting ordinary logic and merely imagining that we doubt it. (C. S. Peirce had a phrase for such imaginary doubts: “paper doubts.”)
In a word, if logic is useful, then usefulness always puts a limit to what anyone can regard in ordinary, practical matters as truly logical, even if a world of alternative logical principles should be somehow “possible.” And in that case (we should add), the logical correctness of ordinary reasoning doesn’t depend on its usefulness; rather, its usefulness depends on its correctness. If we don’t reason in logically correct ways, we get useless results, and what then follows is that the usefulness of the reasoning depends on its correctness, not the other way around.40 In sum, the great mass of practical intuitions that we often call “common sense” will still set boundaries to what anyone can sensibly devise as a plausible system of formal logic.
![]()
Looking back on all these points, we might say that the activity we normally call “reasoning” is rather like a machine and that the ideas of truth and falsity are among this machine’s most vital components. If we then take these components away or try to connect them incorrectly, the machine simply fails to operate. This doesn’t mean reasoning is the be-all and end-all of life, but only that, if we want to reason successfully, we need to meet certain requirements.
Aristotle and the Stoics picked their way carefully through many of these issues, and the medieval logicians who followed inherited a rich legacy. Unlike the static world inhabited much later by many of the medievals, Greek society was in constant flux, and the insight of the logicians of the time was to find continuity and necessity in a world of warring ideas. Despite the varied and vacillating opinions of the day, the Greek logicians saw plainly that the enduring quality of commonplace logical forms, especially those that yield precise and definite results, turned crucially on the law of contradiction and the law of excluded middle. Only much later, in a new, merciless age of mass killings and fanatical terror, did thinkers begin to take logic as a discipline in a radically new direction.