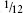of an inch but not 
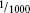of a metre!’The age of great Megalithic building began before 3000 BC and many of the major sites had been abandoned by the middle of the 3rd century BC. The last remnants of the Megalithic builders seem to have disappeared by about 1500 BC, which means that they certainly overlapped with the Minoan culture that clearly used the same 366 method of geometry. From the Iron Age until the rise of the Roman Empire, much of what is now the British Isles and France was inhabited by the Celts. There is no record of whether the Celts inherited any of the weights and measures that had been used by the Megalithic builders but it is not unreasonable to consider that the old units may have survived in an original or in a modified form.
Only with the spread of the Roman Empire did these far western regions of Europe gain a recognizable uniformity in terms of weights and measures. Rome held sway over Gaul (France) and Britain until the beginning of the 6th century AD when the Roman legions were recalled and the area fell into that historically murky period known as the ‘Dark Ages’. The withdrawal of the legions led to a power vacuum in both Britain and Gaul which, through the peculiar set of circumstances prevailing, gave way to feudalism, a system under which international trade was not especially desired or encouraged. However, if any country was going to prosper and grow strong, a degree of cross-border cooperation was inevitable. The process was helped somewhat by the development of important sites of commerce, particularly in the area of northern France which eventually became known as Champagne.
In the 12th and 13th centuries the Champagne fairs, held regularly in specific towns and cities in the region, positively encouraged merchants from all over Europe and beyond to exchange goods. These were huge trade fairs (rather than markets for consumers) that were held under the authority of the dukes of Champagne and new, or apparently new weights and measures appeared at this time. Many British people will be surprised to learn that their much-loved pound and ounce made their first known appearance as French units at these fairs.
It is certain that both units of length and weight were created deliberately to serve the fairs in an attempt to offer common measures that everyone could understand and use without confusion. With the gradual demise in the importance of the fairs and with so much fighting taking place between the emerging nation states of the region, units of length and weight often became a strictly local matter, though frequently with underlying aspects of the old Roman system. Britain struggled but somehow managed with a seemingly incomprehensible muddle of different units, though the country we now know as France was in an even worse state.
Prior to the early 14th century, France was a series of different states which had not been united since Roman times. These were only welded together again as a result of conquests and dynastic unions resulting in virtual chaos, with a wealth of different length, weight and volume unit names and sizes existing simultaneously across the new country. Matters were made even more complicated by the fact that some units retained a common name in different regions even though they differed in size. The chaos continued until some new data on the circumference of the Earth was published in 1670 by Jean Picard, a priest and an astronomer living in La Flèche. Picard accurately assessed the polar circumference of the Earth using the distance from Sourdon near Amiens, to Malvoisine south of Paris, as his test area. This gave another priest an inspired thought.
Father Gabriel Mouton of St Paul’s Church in Lyon put forward the suggestion that France should design a completely original set of decimalized weights and measures based upon an agreed fraction of the length of one minute of arc of the newly-measured polar circumference of the planet. The idea immediately caught the imagination of leading thinkers, but Picard did not agree with Mouton’s suggestion for the means of devising a new linear measure. Instead, together with astronomer Ole Römer (a distinguished scientist from Copenhagen who spent long periods in France and Germany), Picard proposed that the new unit of linear length upon which everything else could be based, should be precisely the length of a pendulum with a beat of one second of time.
The concept of a ‘seconds pendulum’ had been first identified by Galileo earlier in the same century when he became the first recorded European to actively experiment with pendulums, though it was left to the Englishman Isaac Newton (1643–1727) to later establish correct dimensions for the seconds pendulum. The device had a particular fascination for Newton, who experimented extensively in all matters pertaining to gravity. Newton had calculated that a freely-swinging pendulum, at a location of 45 degrees latitude, with a beat of exactly 1 second, would measure 39.14912 inches in length which was correct to within one twenty-five thousandth of a second. (While this is all of great historical interest we demonstrated in the last chapter that the Sumerians had achieved all these objectives some 3,500 years earlier.)
It was known by the time of Picard and Römer that gravity did not act equally on all parts of the planet because the Earth is an oblique spheroid rather than a perfect sphere. The astronomers seem to have favoured basing the new linear unit on the seconds pendulum measured at Paris, though Newton’s 45-degree latitude was also considered, as was a seconds pendulum set for the equator.
Despite the debates about the best way forward nothing further seems to have happened regarding the new French system until the 14th July 1789 when the Bastille was stormed, igniting a revolution that was to change that country for ever. The problem of the disparate weights and measures had been tolerated because there were always greater problems to be confronted but after the revolution, with the beginning of a completely new regime, the populace could be persuaded to change everything it had known for generations in terms of weights and measures.
Only a year after the start of the French Revolution, in 1790, the Constituent Assembly of France was on the receiving end of a report from Charles-Maurice Talleyrand Perigord, Bishop of Autun. Talleyrand was a larger-than-life character and certainly no scientist, yet he resurrected the proposition of a new system of weights and measures, based on a standard to be derived from the length of a pendulum at 45 degrees north (45 degrees being exactly halfway between the equator and the poles.)
The reason for Talleyrand’s interference in such matters probably stemmed from his success as a diplomat. At almost exactly the same time as revolutionary France was thinking in terms of a new measuring system, across the Channel in England scientific minds were also turning in the same direction. Talleyrand desperately wanted to achieve a lasting peace between France and Britain, an heroic effort that was doomed to failure. It is also known that he had friends within the British Royal Society as well as in London-based masonic lodges. He went so far as to suggest collaboration between the Académie des Sciences in Paris and the Royal Society of London in order to try and establish the length of a seconds pendulum to the very highest level of accuracy. At the time, Louis XVI was still clinging to the French throne and the Assembly passed a decree asking Louis to write to the British king, George III. The letter was to suggest that:
‘Parliament should meet with the National Assembly for the fixation of national units of weights and measures so that commissioners of the French Academy could meet with an equal number from the Royal Society in the most convenient place to determine at 45° latitude or at any other preferred latitude the length of the [seconds] pendulum and produce an invariable model for all weights and measures.’
It is unlikely that the request of the French Assembly was ever acted upon by Louis because no trace of such a letter exists in British archives. Louis was a worried man and doubtless thought that to force an entirely new measuring system on a country already so troubled might be the last straw. Almost in tandem with the suggested letter to Britain, the Assembly set up a commission to look into a new metric system. It was composed of five brilliant scientists and mathematicians. These men were Laplace, Lagrange, Monge, Borda and Condorcet. The report produced by this commission was presented to the French Academy on 19th March 1791.
It was at this time that the concept of the seconds pendulum was more or less abandoned as the preferred unit for the new linear measurement because it was reluctantly decided that no timepiece existed that could accurately measure one second of time. The commission was left with no option but to return to Father Mouton’s original suggestion that the new unit should be derived from an extremely accurate assessment of the distance between the North Pole and the equator and to make the new linear unit a subdivision of this distance. Despite this decision, the seconds pendulum was far from forgotten. One of the commission’s recommendations was:
‘To make observations at latitude 45° for determining the number of vibrations in a day, and in a vacuum at sea level, of a simple pendulum equal in length when at the temperature of melting ice, to the ten-millionth part of the meridian quadrant with a view to the possibility of restoring the length of the new standard unit, at any future time, by pendulum observation.’
So the seconds pendulum was retained as a safety backup should the new unit of length ever be lost. This indicates that the French team had chosen a subdivision of polar circumference that was as close to the seconds pendulum as they could achieve using a very round number. They settled on one ten-millionth part of the meridian quadrant – which meant that the new unit was one forty-millionth part the of the polar circumference of the Earth. This unit was eventually to be named the ‘metre’. It is clear from the wording of the report presented by the commission that it was aware of the very slight difference in length between the established seconds pendulum and the proposed linear unit.
The seconds pendulum was still not forgotten, even in the later stages of the drive towards the metric system. The report of the fieldwork was dated 30th April 1799. Among its observations as reported by R. D. Connor was this:
‘The length of a seconds pendulum at Paris at 0° C in vacuum at sea level is 0.99385 metres’. (This last is equivalent to a period of a pendulum of length 1m being 2.00618 seconds at Paris, latitude 48° 52.)
The seconds pendulum corrected metre came into official existence on 10th December 1799. However, the metric system in its entirety did not become obligatory until 1st January 1840. It is surprising how many sources still quote the Emperor Napoleon as having instigated metrication, but nothing could be further from the truth. Napoleon disliked the entire metric system and he is reported to have said:
‘I can understand 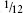of an inch but not 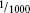of a metre!’
Having set the length for the metre the commission identified their longest unit of length as the kilometre at 1,000 metres, and the shortest was the millimetre at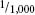 
of the metre. In between they added the centimetre, being ten times larger than a millimetre and 100 times smaller than the metre. Next they turned their attention to the basic units of capacity and mass, which they derived in the simplest manner possible. They took a length of one tenth of a metre (ten centimetres) and used it to dictate the sides of a cube. This cube was then filled with distilled water (under very strict temperature and pressure requirements) and the volume occupied by the water was called a litre, while its weight was designated the kilogram.
Suddenly the metric system had been resurrected. Because the inspiration for the metre had originally been the seconds pendulum and because the French scientists had followed the same logic as their Sumerian forebears, the double-kush was back under a new name!
It appears that none of these French scientists questioned what a second of time actually was or where it had come from, except that it represented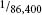 
part of a mean solar day. They knew it had originated from ancient Mesopotamia but the Sumerian culture had not been identified at the time. It was much later that archaeological digs in the sands of Mesopotamia began to turn up scores of cuneiform tablets and slowly some people began to notice the amazing similarities between the Sumerian measurement system and the metric system. Professor Stecchini has shown how there was distinct embarrassment in academic circles at the convergence of a new and scientifically-based system with that of the most ancient documented culture on the planet.
There was once a great deal of controversy regarding Mesopotamian linear lengths, weights and measures and their ‘fit’ with the metric system. It has now become standard academic form to deny that either the Sumerians or the Babylonians could, or would have wanted to, create cubes or one-tenth the double-kush, in order to produce a fullyintegrated measuring system.
The facts are self-evident and the reason why the metric system is so similar to the Mesopotamian model is no puzzle. The metre was chosen on the grounds that it was a provable geophysical unit, adopted because it so closely approximated the seconds pendulum, which itself was captivating scientists from Newton’s time onwards. Indeed, when the Imperial Weights and Measures Acts of the 19th century were passed in Britain, instructions were given that these too were to be checked against the seconds pendulum if the created units were ever lost or damaged.
The French team that did not trust their late 18th-century timepieces would no doubt be amazed to learn that one day their metre would be defined as the distance travelled by light in a vacuum in a time interval of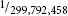 
second. We now have the science to measure such tiny events but it remains a fact that the true seconds pendulum lies behind this definition. Bearing in mind that a pendulum length changes somewhat according to the latitude at which it is checked, the astronomer-priests of old made an extremely good job not only of defining the second of time, but also of showing what it meant in linear terms. The double-kush pendulum ticks away seconds with an error of only one five-thousandth of a second, an error that to anyone except the most fastidious Grand Prix racing driver means nothing!
We had been more than perplexed when we discovered that spheres with diameters measured in Megalithic units produce volumes that conform to cubic metres, litres and metric tonnes. It had seemed ridiculous in the extreme – but now we could see an underlying pattern emerging. The use of the second and the pendulum had drawn the French team into the ancient matrix that held some deep reality from the turning of the Earth. We really needed to understand better what a second of time actually is, but first we decided to see if there were any other recent measurement systems that may provide an additional piece for our giant jigsaw puzzle.
Following the French Revolution the Académie des Sciences decided to introduce a new system of decimal weights and measures that was to be based on the length derived from a pendulum that produced a time interval of one second. Using this ancient Mesopotamian measure of time would have automatically reinvented the double-kush without the fact being realized. Eventually they had to concede that their timepieces were not accurate enough to measure a precise second and they therefore used a subdivision of the globe from the equator to the North Pole as the basis of the new metric system. The metre that was settled upon was one 10,000,000th part of the Earth’s quadrant and extremely close in length to the seconds pendulum that they had originally wanted to achieve.
The seconds pendulum was used as a backup means of recreating the metre and even the imperial system used this same technique for possible emergencies. Having reinvented the double-kush the French then proceeded to reincarnate the ancient Mesopotamian units of weight and capacity by means of cubes that were on a one-tenth subdivision of the metre. Professor Livio C. Stecchini has shown how there was a later realization that this supposedly new, scientifically-based system was virtually identical to the Mesopotamian one used several thousand years before.
We had still not explained why spheres with diameters of Megalithic dimensions produce volumes from the metric system – but we had established that the ‘metric’ system was far from a recent invention as is generally claimed.