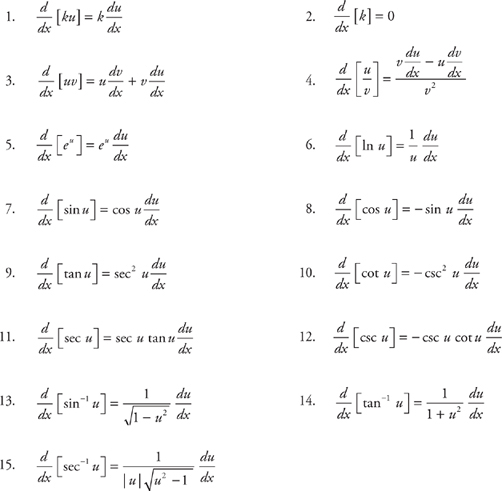
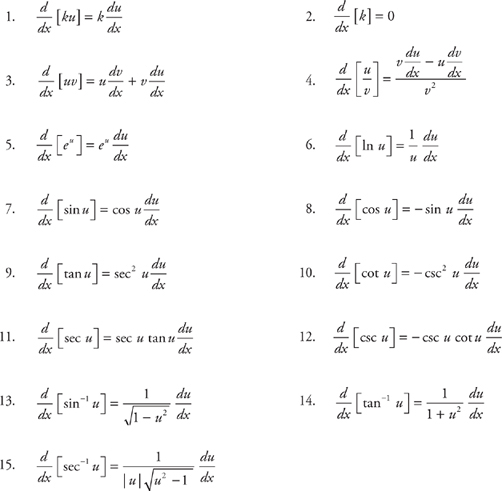
One of the biggest problems that students have with calculus is that their algebra, geometry, and trigonometry are not solid enough. In calculus, you’ll be expected to do a lot of graphing. This requires more than just graphing equations with your calculator. You’ll be expected to look at an equation and have a “feel” for what the graph looks like. You’ll be expected to factor, combine, simplify, and otherwise rearrange algebraic expressions. You’ll be expected to know your formulas for the volume and area of various shapes. You’ll be expected to remember trigonometric ratios, their values at special angles, and various identities. You’ll be expected to be comfortable with logarithms. And so on. Throughout this book, we spend a lot of time reminding you of these things as they come up, but we thought we should summarize them here at the end.
When you multiply exponential expressions with like bases, you add the powers.
xa • xb = xa+b
When you divide exponentiated expressions with like bases, you subtract the powers.

When you raise an exponentiated expression to a power, you multiply the powers.

When you raise an expression to a fractional power, the denominator of the fraction is the root of the expression, and the numerator is the power.
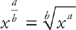
When you raise an expression to the power of zero, you get one.
x0 = 1
When you raise an expression to the power of one, you get the expression.
x1 = x
When you raise an expression to a negative power, you get the reciprocal of the expression to the absolute value of the power.

A logarithm is the power to which you raise a base, in order to get a value. In other words, logbx = a means that ba = x. There are several rules of logarithms that you should be familiar with.
When you take the logarithm of the product of two expressions, you add the logarithms.
log(ab) = log a + log b
When you take the logarithm of the quotient of two expressions, you subtract the logarithms.
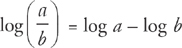
When you take the logarithm of an expression to a power, you multiply the logarithm by the power.
log(ab) = b log a
The logarithm of 1 is zero.
log 1 = 0
The logarithm of its base is 1.
logb b = 1
You cannot take the logarithm of zero or of a negative number.
In calculus, and virtually all mathematics beyond calculus, you will work with natural logarithms. These are logs with base e and are denoted by ln. Thus, you should know the following:
ln 1 = 0
ln e = 1
ln ex = x
eln x = x
The change of base rule is: 
The area of a triangle is  (base)(height).
(base)(height).
The area of a rectangle is (base)(height).
The area of a trapezoid is  (base1 + base2)(height).
(base1 + base2)(height).
The area of a circle is πr2.
The circumference of a circle is 2πr.
The Pythagorean theorem states that the sum of the squares of the legs of a right triangle equals the square of the hypotenuse. This is more commonly stated as a2 + b2 = c2 where c equals the length of the hypotenuse.
The volume of a right circular cylinder is πr2h.
The surface area of a right circular cylinder is 2πrh.
The volume of a right circular cone is  πr2h.
πr2h.
The volume of a sphere is  πr3.
πr3.
The surface area of a sphere is 4πr2.
Given a right triangle with sides x, y, and r and angle θ below:
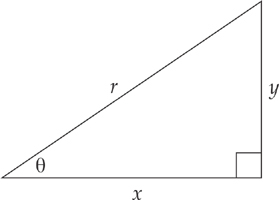
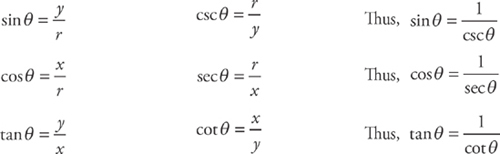

sin(A + B) = sin A cos B + cos A sin B
sin(A – B) = sin A cos B – cos A sin B
cos(A + B) = cos A cos B – sin A sin B
cos(A – B) = cos A cos B + sin A sin B
You must be able to work in radians and know that 2π = 360°.
You should know the following:
